树形动规题型分析

我们已经学过了枚举法，有时还需要先分类再按一定顺序进行枚举?接下来我们将要学习如果对某件事情的过程进行枚举，一般会使用另一种方法：树形图法?所谓树形图法就是用像树一样的、不断分叉的图来表示出所有情况的方法画出树形图与一棵树的生长过程类似，先从“树根”开始，然后不断长出新的“树枝每次长出新的“树枝”时都有可能产生分叉，最后长满了“果实这样一直下去把所有情况都画完，最后数一下“果实”的数目即可例题 1 乌龟、兔子、米老鼠站成一排，如果乌龟不站在第 1 个，兔子不站在第 2 个米老鼠不站在第 3 个，请问它们共有多少种不同的站法?分析：第 1 个位置可以站哪些小动物？第 2 个位置呢？以第一动物位置站的人作为“树根” 表用树形图示出所有的站法.甲、乙、丙4个人站队，站成一条直线?如果甲不站第1、2 个，乙不站第2、3个，丙不站第3、4 个丁不站第4、1 个，那么一共有多少种站队的方法?b厂第十四讲\r1树形图II. fi li (小高、墨莫和萱萱玩传球游戏，每次持球人都可以把球传给另外两人中的任 何一人 . 先由小高拿球，第 1 次传球可以传给其他两人中的任何一人，经过 次传球之后，球又回到了小高手里 . 请问一共有多少种不同的传球过程 ?分析：第 1 次有多少种传法？试着用树形图画出每次传球后给谁 里 上才是符合题意的传法 .不同，一共有多少个满足条件的四位数 ?分析：四位数的千位数字和个位数字分别有几种情况？应该选择哪个数位的数字作为: 练习 3）一个三位数 位上的数字都是 5、6、 7 中的某一个，并且相邻的两个数字不相同，一共有多少个满足条件的三位数 ?☆题2注意：只有第 4 次传球后回到小高手练习 2有 A 、B 、C 三片荷叶 ' 青蛙另一片荷叶上，结果它跳了呱呱”在荷叶 A 上，每次它都会从一片荷叶跳到3次之后，不在荷叶 A 上. 请问：它一共有多少种不同的跳法 ?例题 3一个四位数，每一位上的数字都是0、1、2 中的一个，并且相邻的两个数字树根”来画树形例题 4王老师有一个带密码锁的公文包，但是他忘记了密码 . 只记得密码是一个三位数. 这个三位数的个位数字比十位数字大，十位数字比百位数字大，并且没有比 5 大的数字 . 试问：王老师最多需要试多少次就肯定能打开这个公文包 画出树形图卜析：百位数字最小， 有几种情况？把这些情况分别作为“树根”一个三位数，百位比十位大，十位比个位大，个位不小于数一共有几个？例题5常昊与古力两人进行围棋赛，谁先胜三局就赢得比赛. 如果最后常昊获胜了，那么比赛的进程有多少种可能？分析：试着把每场比赛的结果用树形图表示出来?注意：不会有古常----- 古古- 常——（常）这样的过程出现，因为在这种情况下，赛完第 4 场后古力已经获胜，不符合题意.例题65 块六边形的地毯拼成了如下图的形状，每块地毯上都有一个编号，现在小高站在1 号地毯上，他想要走到5 号地毯上?如果小高每次都只能走到和他相邻的地毯上（两个六边形如果有公共边就成为相邻），并且只能向右边走，例如1f 2—3—5 就是一种可能的走法. 请问：小高一共有多少种不同的走法？分析：注意开始是从 1 号毯开始，结束在 5 号地毯才能符合题意汽车品牌家族树形图甲、乙、丙三个人传球，从甲开始传球，每次拿球的人都把球传给剩下两个人中的一人，传了次后球在丙的手上，那么一共有多少种可能的传球过程？2.且相邻的两个数字不一样，那么卡莉娅最多试多少次就一定能打开日记本？3. 粗心的卡莉娅忘记了日记本的三位密码，只记得密码是由1、2、7 三个数字中的某些数字构成的，4. 甲、乙比赛乒乓球，五局三胜. 已知甲胜了第 1 局，并最终获胜. 请问一共有多少种不同的比赛过程？5. 满足下面性质的数称为阶梯数：它的百位数字比十位数字小，十位数字比个位数字小，并且相邻两位数字的差不超过 2 . 例如：135 、234 为阶梯数，156 就不是阶梯数，那么共有多少个三位数是阶梯数？☆2种 121233龟兔鼠鼠龟兔212312344墨■墨小小萱萱小 墨萱小墨墨曰311222211212 2 2 1001 22141 第十四讲 树形图可以画成树形图，如下图，共详解 1 次可以给萱萱可以画成树形图，第8 种， 2 的也有 8 种，共 16树根有 1 的共有1、2 4 10 次2、3 三个数作为树可以画出三幅树形分别详例题 答案 例题答例题 答案 详解 例题 答案详解 种.1 2种2 6种3 16 种可以画成树形图，如下图，树根有 也可以给墨莫，如下图，共 6 种5. 例题 5答案：10 种6. 例题 6答案： 5 种详解：可以画成树形图，共有 5 种.4535245 145 3572种12341243甲甲甲乙丙丁 甲乙丁 丁8123 123 BBAACCCBBCAAC练习93答案简答 练习 答案 简答 6种 12 种 2 6种3 次后不在 A 荷叶上，如下图，共可以画成树形图，如下图，树根B 、 C 荷叶上 跳了 5、6、7 树根是 5的共有 4种，6 的也有 4种，7的也有 4 种，共 12可以画成树形图，第 1 次可跳在B丙 练习 1 答案： 2 种 简答：可以画成树 形图，如下图，共510 练习答案：简答：7610 种可以画成树形图，从个位开始枚举如下图，共百＞98581 作业 11答案：342;423简答：可以画成树形图3、4 2、2、3 12 作业 23答案：3简答：可以画成树形图710 种百＞513. 作业3简答：如下图. 首位是 2 或7 开头的密码也有 4 个，所以符合条件的有12 个，最多要试12 次.14. 作业 4答案：615. 作业 5答案：24 个简答：如下图，可分别画出百位是1、2、3、4、5、6、7的树形图，百位为1的有4种，百位为2的有4 种，百位为 3 的有 4 种，百位为 4 的有 4 种，百位为5 的有 4 种，百位为6 的有 3 种，百位为7 的有 1 种，共有24 个阶梯三位数.甲丙乙丙甲丙甲丙乙丙13. 作业 3答案：12简答：如下图．首位是2 或 7 开头的密码也有 4 个，所以符合条件的有 12 个，最多要试 12次．百十个127 117214. 作业 4答案： 6简答：可以画成树形图：1、 2 、 3、 4、 5 、 6、 7 的树形图，百位为 1 的有 4 种，百 位为 2 的有 4 种， 百位为 3 的有 4 种，百位为 4 的有 4 种，百位为 5 的有 4 种，百位为 6 的有 3 种，百位为 7 的有 1 种，共有 24 个阶梯三位数． 甲甲甲乙 乙甲甲乙 甲乙乙 甲15. 作业 5答案：24 个简答：如下图， 可分别画出百位是。

a)树型动规基本模型根—>叶叶－>根：既根的子节点传递有用的信息给根，完后根得出最优解的过程。

给出一棵树，每个结点有一个权，求一棵子树，使得其顶点的权值最大；或者给出一棵树．树边有一个权代表结点间的距离，对每个结点，求出它到其他结点的最远距离。

这两个问题用树型动态规划来做的话都是O(n)的。

例：二叉苹果树问题描述有一棵苹果树，如果树枝有分叉，一定是分2叉（就是说没有只有1个儿子的结点）这棵树共有N个结点（叶子点或者树枝分又点），编号为卜N，树根编号一定是1。

我们用一根树枝两端连接的结点的编号来描述一根树枝的位置。

2 5 现在这颗树枝条太多了，需要剪枝。

但是一些树枝有苹\ / 果。

给定需要保留的树枝数量，求出最多能留3 4 住多少苹果。

\ /1问题分析：f[k，j]表示以结点k为父结点的子树中，保留j个树枝能留住的最多苹果数量，f[k,0]=0;f[k,1]=c[k]; 子结点树枝和为j-1;则状态转移方程为：f[k，j]:=max{f[son[k,1], i]+f[son[k,2], j-I-1]+c[k]} (2≤J≤q+1;0≤i≤J;)，f[1,q+1]为最优解。

vara,b:array[0..100,0..100]of integer;son:array[1..100,1..2]of integer;s,c:array[1..100]of integer;n,q,i,j,si,x,y:integer;procedure maketree(k:integer);{建树并在s数组中储存树的后序遍历}vari,j:integer;beginif k=0 then exit;{表示k的父亲已没有儿子}j:=0;for i:=1 to n doif a[k,i]>=0then begininc(j);son[k,j]:=i;{记录第j个儿子}a[i,k]:=-1;c[i]:=a[k,i];{记录I点的值}if j=2 then break;end;maketree(son[k,1]);maketree(son[k,2]);inc(si);s[si]:=k;{s数组记录数的后序}end;procedure tree(k:integer);vari,j:integer;beginif son[k,1]=0then begin{k没有孩子}for i:=1 to q+1 dob[k,i]:=c[k];endelse beginb[k,1]:=c[k];for j:=2 to q+1 dofor i:=0 to j-1 doif b[k,j]<b[son[k,1],i]+b[son[k,2],j-i-1]+c[k]then b[k,j]:=b[son[k,1],i]+b[son[k,2],j-i-1]+c[k];end;end;beginreadln(n,q);for i:=1 to n dofor j:=1 to n doa[i,j]:=-1;fillchar(son,sizeof(son),0);fillchar(b,sizeof(b),0);for i:=1 to n-1 dobeginreadln(x,y,a[x,y]);a[y,x]:=a[x,y];end;si:=0;maketree(1);for i:=1 to n dotree(s[i]);writeln(b[1,q+1]);end.。

2018福建三明公务员考试行测技巧：被遗忘的植树问题1.两端不植树的问题是指在线路的两个端点不进行植树的问题，可以延伸为植树、插旗杆、路灯等。

例如：在一条长2500米的公路一侧架设电线杆，每隔50米架设一根，若公路两端都不架设，共需电线杆多少根。

此时电线杆就相当于我们植树问题中的树，公路两端不架设说明路的两端不植树，要求的电线杆的根数则是求两端不植树的情况下给定间隔长求树的棵树的问题。

公式：棵树=距离÷间距-1.2.两行植树的问题是指在路的两旁都需要进行植树的问题，可以延伸为植树、插旗杆、路灯等。

例如：在一条长50米的跑道两旁,从头到尾每隔5米插一面彩旗,一共插多少面彩旗?此时彩旗就相当于我们植树问题中的树，跑道两旁需要插旗说明路的两行都要植树，要求彩旗数则是求两行植树的情况下给定间隔长求树的棵树的问题。

公式：路线两端及两行都要植树：棵树=(距离÷间隔+1)×2路线两行植树但是两端不植树：棵树=(距离÷间隔-1)×2【例题1】某单位购买一批树苗计划在一段路两旁植树。

若每隔5米种1棵树，可以覆盖整个路段，但这批树苗剩20棵。

若每隔4米种1棵树且路尾最后两棵树之间的距离为3米，则这批树苗刚好可覆盖整个路段。

这段路长为( )。

A.195米B.205米C.375米D.395米解法二：对比两种植树方案，第二种比第一种每行多用了10棵树，故多了4×10-1=39米，除了这10棵树，两种方案用的树的数量是相同的，因此同样数量的树隔5米和隔4米差的总长应该和多出来的10棵树多的总长相等，两种方案每种间隔差1米，故多出来的39米是39个间隔多出来的总长，因此，路的总长为39×5=195米。

【总结】当题目中出现每隔多少米植一棵树的关键词，可知此题是等间距植树问题，所以总长是树间隔的倍数，若路两端植树，则总长等于(树的数量-1)×间隔，若两端不植树，则总长等于(树的数量+1)×间隔。

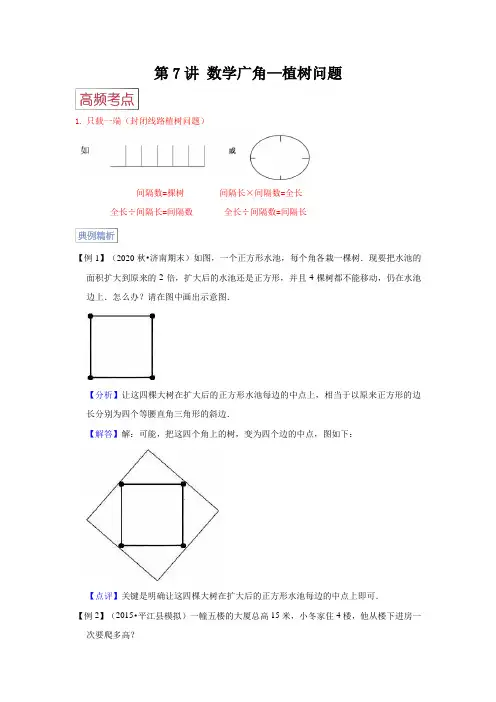
第7讲数学广角—植树问题1.只载一端（封闭线路植树问题）间隔数=棵树间隔长×间隔数=全长全长÷间隔长=间隔数全长÷间隔数=间隔长【例1】（2020秋•济南期末）如图，一个正方形水池，每个角各栽一棵树．现要把水池的面积扩大到原来的2倍，扩大后的水池还是正方形，并且4棵树都不能移动，仍在水池边上．怎么办？请在图中画出示意图．【分析】让这四棵大树在扩大后的正方形水池每边的中点上，相当于以原来正方形的边长分别为四个等腰直角三角形的斜边．【解答】解：可能，把这四个角上的树，变为四个边的中点，图如下：【点评】关键是明确让这四棵大树在扩大后的正方形水池每边的中点上即可．【例2】（2015•平江县模拟）一幢五楼的大厦总高15米，小冬家住4楼，他从楼下进房一次要爬多高？【分析】五层楼总高15米，那么每层的高度是15÷5＝3米，小冬家住4楼，他从楼下进房一次要爬4﹣1＝3个楼间距，然后用3乘每层的高度即可解决问题．【解答】解：15÷5×（4﹣1）＝3×3＝9（米）答：他从楼下进房一次要爬9米高．【点评】本题属于植树问题的实际应用，关键是明确：间隔数＝层数﹣1．【例3】（2014春•杭州期末）为了保护公园里的一棵千年古树，园林局决定为它做一个圆形防护栏．如果护栏有10个间隔，一共需要打多少根木桩？【分析】根据植树的知识知道，在圆形的周围植树，间隔数就是植树的棵数，而本题中的防护栏是个圆形的，护栏有10个间隔，所以即可得出需要打木桩的根数．【解答】解：因为在圆形的防护栏周围打木桩，有几个间隔就必须打几个木桩，所以如果护栏有10个间隔，一共需要打10根木桩；答：一共需要打10根木桩．【点评】此题属于在圆形的物体周围植树的问题，即在圆形的周围植树，间隔数就是植树的棵数．2.两端都载:如图:间隔数＋1=棵树间隔长×间隔数=全长全长÷间隔长=间隔数全长÷间隔长+1=棵数全长÷间隔数=间隔长全长÷（棵树－1）=间隔长【例4】（2015•平江县模拟）在一段路的路边每隔20米栽一棵树，包括这段路两端在内栽10棵树，这段路长多少米？【分析】由于从一端到另一端一共栽了10棵树，共有间隔数为：10﹣1＝9个；又由于间距是20米，根据总距离＝间距×间隔数可以求出这条路的长度，列式为：20×9＝180（米）；据此解答．【解答】解：根据分析可得，20×（10﹣1）＝20×9＝180（米）；答：这段路长180米．【点评】本题考查了植树问题，知识点是：栽树的棵数＝间隔数+1（两端都栽），总距离＝间距×间隔数．【例5】（2015春•长春校级期末）工人叔叔要在马路的一侧安装路灯，从头开始每隔4米安一个，共安装了30个，这条路长米．【分析】因为间隔数＝路灯的盏数﹣1，所以先求出马路边路灯的间隔数，再乘4即可．【解答】解：（30﹣1）×4＝29×4＝116（米）答：这条路长116米．故答案为：116．【点评】本题主要考查了间隔数＝树的棵数﹣1，再根据基本的数量关系解决问题．【例6】（2015春•务川县期中）小朋友们在路的一边植树，先植一棵树，以后每隔3米植一棵，已经植了9棵，问第一棵和第九棵树相距多少米？【分析】此题属于植树问题中的两端都要栽的情况：间隔数＝植树棵数﹣1，据此可得一共有9﹣1＝8个间隔，再乘每个间隔的长度3米，即可得出第一棵和第九棵树相距多少米．【解答】解：（9﹣1）×3，＝8×3，＝24（米）；答：第一棵和第九棵树相距24米．【点评】植树问题中：两端都要栽时，间隔数＝植树棵数﹣1．3.两端都不载如图:间隔数－1=棵树间隔长×间隔数=全长全长÷间隔长=间隔数全长÷间隔数=间隔长全长÷间隔长－1=棵数全长÷（棵树＋1）=间隔长【例7】（2016春•魏县校级月考）某木工把一根长4米的圆柱形木料锯成80厘米的小段，需40分钟；如果改锯成50厘米的小段，需要多少时间？【分析】根据题意，先求出长4米的圆柱形木料锯成80厘米的小段需要锯多少次，再求出每锯一次所需要的时间，即可求出锯成50厘米的小段所需要的时间．【解答】解：4米＝400厘米，400÷80﹣1＝4（次），40÷4＝10（分钟），400÷50﹣1＝7（次），10×7＝70（分钟），答：需要70分钟．【点评】解答此题的关键是，要知道锯木料的次数比锯成的段数少1，再根据题中的数量关系即可解答．【例8】（2015春•永胜县月考）一根钢管，把它锯成7段，需要18分钟，照这样计算，如果锯成16段需要多少分钟？【分析】锯两段只需要锯1次，所以锯成7段，需要锯（7﹣1）次，用18分钟除以这个时间，就是锯一次用的时间；锯16段只需要锯16﹣1＝15次，用锯一次用的时间乘上15就是锯成9段需要的时间．【解答】解：18÷（7﹣1）＝18÷6＝3（分钟）3×（16﹣1）＝3×15＝45（分钟）答：如果锯成16段需要45分钟．【点评】本题关键是要理解锯1次就可以锯成2段，存在这个关系：锯成的段数＝锯的次数+1．【例9】（2013秋•即墨市期末）崂山举行登山大赛，组委会在长达845米的山路中，每隔65米设置一个服务站（起点和终点不设）．共设多少个服务站？【分析】先用全程除以间隔的长度，求出一共有多少段，再用段数减去1就是需要设服务站的数量．【解答】解：845÷65﹣1＝13﹣1＝12（个）答：共设12个服务站．【点评】本题属于植树问题中的两段都不栽的情况：植树的棵数＝间隔数﹣1．一．选择题（共8小题）1．（2021秋•盐都区期末）把一根电缆截成2段需要4分钟，如果截成5段需要（）分钟．A．10B．20C．162．（2020秋•黔西南州期末）一根绳子长15米，剪了三刀剪成（）段．A．3B．4C．53．（2019秋•东海县期中）大上海国际公寓步行街上两边张灯结彩，从这头到那头每隔4米挂一个红灯笼（两端都挂），步行街全长600米，一共挂了多少个红灯笼？（）A．150B．151C．302D．3004．（2021秋•巴马县期末）一根钢筋锯成6段，共需30分钟，平均锯一次需要（）分钟．A．5B．7C．6D．45．（2015秋•利川市月考）圆形滑冰场的一周全长180m．在这个滑冰场的一周每隔12m安装一盏灯，一共要安装（）盏灯．A．14B．15C．166．（2021秋•老城区期末）公园内一条林荫大道全长800米，在它的两侧从头到尾每隔20米放一个垃圾桶，一共需要（）个垃圾桶。

描述Description设一个n个节点的二叉树tree的中序遍历为（l,2,3,…,n），其中数字1,2,3,…,n为节点编号。

每个节点都有一个分数（均为正整数），记第i个节点的分数为di，tree及它的每个子树都有一个加分，任一棵子树subtree（也包含tree本身）的加分计算方法如下：subtree的左子树的加分×subtree的右子树的加分＋subtree的根的分数若某个子树为空，规定其加分为1，叶子的加分就是叶节点本身的分数。

不考虑它的空子树。

试求一棵符合中序遍历为（1,2,3,…,n）且加分最高的二叉树tree。

要求输出；（1）tree的最高加分（2）tree的前序遍历输入格式Input Format第1行：一个整数n（n＜30），为节点个数。

第2行：n个用空格隔开的整数，为每个节点的分数（分数＜100）。

输出格式Output Format第1行：一个整数，为最高加分（结果不会超过4,000,000,000）。

第2行：n个用空格隔开的整数，为该树的前序遍历。

样例输入Sample Input55 7 1 2 10样例输出Sample Output1453 1 24 5时间限制Time Limitation每点1s参考程序：var i,j,k,n,m,t:longint;a:array[0..10000] of longint;f,g:array[0..1000,0..1000] of longint;procedure treedp(l,r:longint);var i,j:longint;beginif l>r then begin f[l,r]:=1;exit;end;if l=r then begin f[l,r]:=a[l];g[l,r]:=l;exit;end;if f[l,r]<>0 then exit;for i:=l to r dobegintreedp(l,i-1);treedp(i+1,r);t:=a[i]+f[l,i-1]*f[i+1,r];if t>f[l,r] then begin f[l,r]:=t;g[l,r]:=i;end;end;end;procedure pre(l,r:longint);beginwrite(g[l,r],' ');if l<=g[l,r]-1 then pre(l,g[l,r]-1); if g[l,r]+1<=r then pre(g[l,r]+1,r); end;procedure print;beginwriteln(f[1,n]);pre(1,n);writeln;end;beginreadln(n);for i:=1 to n dobeginread(a[i]);end;fillchar(f,sizeof(f),0);fillchar(g,sizeof(g),0);treedp(1,n);print;end.。

2018国家公务员考试：关注绿色,行测中的植树问题关注环境，人人有责。

那在行测考试中，就有一类题型体现了我们对于“绿色”的向往——植树问题。

这类问题如何处理呢，中公教育专家在此进行指导。

植树问题是数量关系的一种常见题型。

植树问题通常是指沿着一定的路线植树，这条路线的总长度被树平均分成若干个段，由于路线不同、植树要求不同，路线被分成的段数和植树的棵数之间的关系就不同。

那么，下面我们来看下段数与植树的棵数之间的关系。

一、在线段上的植树问题可以分为以下三种情形：1，直线上，如果两端都植，那么：棵数= 段数+12，直线上，如果只植一端，那么：棵数=段数3，直线上，如果两端都不植，那么，棵数=段数-1二、在封闭线路上植树，那么：棵数=段数知道了段数和植树的棵数之间的关系，那么我们得到棵数、总路长、间距之间的关系：(一)线段上的植树问题依然分为以下三种情形：1.两端都植树：两个端点都植树，植树的棵数=段数+1，结合段数=总路长÷间距，则：棵数=总路长÷间距+1，总路长=(棵数-1)×间距。

2.只有一端植树：只有一个端点植树，植树的棵数=段数，结合段数=总路长÷间距，则：棵数=总路长÷间距，总路长=棵数×间距。

3.两端都不植树：两个端点都不植树，植树的棵数=段数-1，结合段数=总路长÷间距，则：棵数=总路长÷间距-1，总路长=(棵树+1)×间距。

注：以上是单边植树的情况，如果是双边植树，注意结合单边植树的公式进行转化。

(二)封闭植树：结合种树的棵数=段数，则：棵数=总路长÷间距，总路长=棵数×间距。

下面，我们来看下植树问题的题目。

【例1】某单位购买一批树苗计划在一段路两旁植树。

若每隔5米种1棵树，可以覆盖整个路段，但这批树苗剩20棵。

若每隔4米种1棵树且路尾最后两棵树之间的距离为3米，则这批树苗刚好可覆盖整个路段。

2016年青海事业单位考试行测技巧：透彻分析植树问题【导读】在事业单位备考到来之季，中公事业单位考试网为帮助考生更好的备考行测考试，特意准备了2016年行测答题技巧《透彻分析植树问题》，助力考生顺利通过事业单位行测考试。

植树问题是在一定的线路上，根据总路程、间隔长和棵数进行植树的问题。

一、在线段上的植树问题可以分为以下三种情形。

1、如果植树线路的两端都要植树，那么植树的棵数应比要分的段数多1，即：棵数=间隔数+1。

2、如果植树线路只有一端要植树，那么植树的棵数和要分的段数相等，即：棵数=间隔数。

3、如果植树线路的两端都不植树，那么植树的棵数比要分的段数少1，即：棵数=间隔数-1。

4、如果植树路线的两边与两端都植树，那么植树的棵数应比要分的段数多1，再乘二，即：棵树=段数+1再乘二。

二、在封闭线路上植树，棵数与段数相等，即：棵数=间隔数。

三、在正方形线路上植树，如果每个顶点都要植树。

则棵数=(每边的棵数-1)×边数。

1 非封闭线路上的植树问题主要可分为以下三种情形：⑴如果在非封闭线路的两端都要植树，那么：株数=段数+1=全长÷株距+1全长=株距×(株数-1)株距=全长÷(株数-1)⑵如果在非封闭线路的一端要植树，另一端不要植树，那么：株数=段数=全长÷株距全长=株距×株数株距=全长÷株数例题：长方形场地：一个长84米，宽54米的长方形苹果园中，苹果树的株距是2米，行距是3米.这个苹果园共种苹果树多少棵?解法一：①一行能种多少棵?84÷2=42(棵) 。

|②这块地能种苹果树多少行?54÷3=18(行) 。

③这块地共种苹果树多少棵?42×18=756(棵) 。

如果株距、行距的方向互换，结果相同：(84÷3)×(54÷2)=28×27=756(棵) 。

解法二：①这块地的面积是多少平方米呢?84×54=4536(平方米) 。

2020国考行测数量关系：植树问题变形记在行测数量关系考试中，考生经常会在做题是觉得这个问题没学过，但一看答案顿时恍然大悟“啊，这是我之前学过的一类题型呀”。

之所以大家会有这样的反应是因为出题人在基础题型上面蒙了一层神秘的面纱，现在中公教育专家就来揭开植树问题方面的神秘面纱，告诉大家植树问题是如何变形的。

一、上楼梯问题【例1】闺蜜几人出去旅行，小红的房间在宾馆的第10层，从宾馆大堂一层至小红所在的楼层乘电梯需要耗时27秒，闺蜜小华的房间在宾馆的第16层，则电梯从小红的房间所在的楼层至小华房间所在的楼层，需要耗时多久?A.16B.43C.18D.48【中公解析】这道题目看似表述的是在上楼梯，其实本质上就是植树问题，从1层的大堂到小红第10层的房间，电梯走过的距离是9段楼层之间的间隔且每段间隔是相等的，9段距离共耗时27秒,则每段距离耗时27÷9=3秒。

从小红所在的第10层至小华所在的第16层，共有6段距离，则需要耗时6×3=18秒,所以本题选择C项。

二、锯木问题【例2】木材厂的工人把一根圆木锯成9段，需要耗时24分钟，如果把相同的两根圆木分别锯成15段，需要耗时多少分钟?A.42B.84C.45D.90【中公解析】本题看似是锯木头的一类问题，但其本质还是植树问题。

工人把木头切割成9段需要切割8刀，切割8刀共耗时24分钟，则平均切割1刀耗时24÷8=3分钟。

把一根圆木切割成15段应切割14刀，耗时为14×3=42分钟，则把两根圆木分别锯成15段应耗时42×2=84分钟，所以本题选择B项。

三、排队问题【例3】阅兵式上，准备接受检阅的一列坦克车队共有20辆坦克，每辆坦克车长6米，前后每两辆坦克之间的距离为10米，车队每分钟行驶120米，这列坦克车队要通过290米的检阅场地，需要耗时几分钟?A.7B.6C.5D.4【中公解析】本题坦克车队的总长度是由这20辆坦克车的长度和每两辆坦克车之间的距离共同组成的。

行测植树问题答题技巧精讲行测植树问题是一个相对常见的题型，其涉及的知识点和题型变化也比较多。

为了帮助考生更好地掌握这一题型，我们将在这里详细讲解行测植树问题的答题技巧。

一、了解基本概念在行测植树问题中，有一些基本的概念需要了解，比如树的种类、树的年龄、树的间距等。

这些基本概念对于理解题目和确定答案都有重要的作用。

因此，在答题前，一定要先了解清楚这些基本概念。

二、熟悉常见题型行测植树问题的题型比较多，比如直线植树问题、环形植树问题、方阵植树问题等。

每种题型都有其特定的解题方法和思路。

因此，在备考过程中，需要熟悉各种常见题型，掌握其解题方法和思路。

三、掌握基本公式在行测植树问题中，有一些基本的公式需要掌握，比如直线植树问题的公式：棵数=段数+1；环形植树问题的公式：棵数=段数等。

这些公式可以帮助我们快速计算出答案。

当然，前提是我们要理解公式的含义和应用场景。

四、注意审题在答题过程中，审题是非常重要的。

需要认真阅读题目，理解题目的意思和要求，确定题目所属的题型和需要求解的问题。

只有审清题目，才能确保答题的正确性。

五、画图帮助理解对于一些比较复杂的题目，可以通过画图来帮助理解。

比如环形植树问题，可以画出一个环形图来帮助确定棵数和段数的关系。

画图可以更加直观地展示问题的本质，有助于我们找到解题的思路和方法。

六、多练习多总结行测植树问题需要多做练习才能掌握其解题方法和思路。

在练习过程中，要注意总结各种题型的解题方法和思路，形成自己的知识体系。

同时，也要注意积累一些常用的技巧和方法，比如如何快速确定棵数和段数的关系等。

通过不断地练习和总结，可以逐渐提高自己的解题能力和效率。

七、避免常见错误在解答行测植树问题时，有一些常见的错误需要避免。

比如没有认真审题、理解错误题意、计算错误等。

这些错误都可能导致我们得出错误的答案。

因此，在答题过程中，需要保持警惕，认真审题和计算，确保答题的正确性。

总之，行测植树问题虽然涉及的知识点和题型变化比较多，但只要掌握了基本的解题方法和思路，多做练习和总结，就可以逐渐提高自己的解题能力和效率。