北师大版初二数学秋季班(学生版) 第10讲 解二元一次方程组--基础班
- 格式:docx
- 大小:708.34 KB
- 文档页数:13



第10讲 二元一次方程组知识点1 二元一次方程的概念方程220x y +=、23+1035x y +=,它们都含有两个未知数,并且含有未知数的项的次数都是1.像这样的方程,叫做二元一次方程. 二元一次方程需要满足的条件: 1、只含有两个未知数; 2、含未知数项的最高次数是1; 3、整式方程.【典例】1.若方程3(25)28a bb xy x y --+-=是关于x y ,的二元一次方程,则______a b +=.【答案】3【解析】解:由题意可知:250b -=且31a b -=. 解得:7562a b ==,. ∴7511623a b +=+=. 故答案为:113.【方法总结】有关二元一次方程的定义及其相关概念的问题,一般从其定义或概念需要满足的条件入手,通过建立方程模型,从而求出待定系数或相关字母值.【随堂练习】1.(2019春•新化县期末)下列各式中是二元一次方程的是( ) A .240x y --=B .3x -C .0x y z ++=D .20x y -=【解答】解:A 、该方程是二元二次方程的,故本选项错误;B 、3x -不是方程,故本选项错误;C 、该方程中含有3个未知数,属于三元一次方程,故本选项错误;D 、该方程符合二元一次方程的定义,故本选项正确.故选:D .2.(2019春•嘉兴期末)下列属于二元一次方程的是( ) A .20x y +=B .20x y -=C .21x y=+ D .12y x +【解答】解:A 、该方程中含有两个未知数,但是未知数的最高次数是2,不属于二元一次方程,故本选项错误.B 、该方程中符合二元一次方程的定义,故本选项正确.C 、该方程不是整式方程,不属于二元一次方程,故本选项错误.D 、它不是方程,故本选项错误.故选:B .3.(2019春•满城区期末)已知关于x ,y 的方程22146m n m n x y --+++=是二元一次方程,则m ,n 的值为( )A .1m =-,1n =B .1m =,1n =-C .1m =,4n =D .13m =-,43n =【解答】解:方程22146m n m n x y --+++=是二元一次方程, ∴22111m n m n --=⎧⎨++=⎩,解得:11m n =⎧⎨=-⎩,故选:B .4.(2019春•道外区期末)下列方程是二元一次方程的是( ) A .90x +=B .27x a -=C .39ab =D .17y x+=【解答】解:A 、该方程是一元一次方程,故本选项错误;B 、该方程是二元一次方程,故本选项正确;C 、该方程是二元二次方程,故本选项错误;D 、该方程是分式方程,故本选项错误;故选:B .5.(2019春•杜尔伯特县期末)若||2018||3(2019)(4)2019m n m x n y ---++=是关于x ,y 的二元一次方程,则( ) A .2019m =±,4n =± B .2019m =-,4n =± C .2019m =±,4n =-D .2019n =-,4n =【解答】解:||2018||3(2019)(4)2019m n m x n y ---++=是关于x ,y 的二元一次方程, ∴20190||2018140||31m m n n -≠⎧⎪-=⎪⎨+≠⎪⎪-=⎩,解得:2019m =-、4n =, 故选:D .6.(2018秋•万州区期末)若|21|(1)10250m m x y --+=是关于x 的二元一次方程,则m 的值是( ) A .0或1B .0C .1D .任何数【解答】解:依题意得:|21|1m -=,且10m -≠, 解得0m =. 故选:B .7.(2019春•洛宁县期中)下列方程中,是二元一次方程的是( ) A .46x y +=B .690xy +=C .324x y z -=D .2x l y=+ 【解答】解:A 、是二元一次方程,故此选项正确;B 、是二元二次方程,故此选项错误;C 、是三元一次方程,故此选项错误;D 、是分式方程,故此选项错误;故选:A .8.(2019春•道里区期末)若方程(3)24m x y --=是关于的x ,y 二元一次方程,则m 的取值范围是( ) A .0m ≠B .3m ≠C .3m ≠-D .2m ≠【解答】解:方程(3)24m x y --=是关于的x ,y 二元一次方程, 30m ∴-≠,即3m ≠,故选:B .知识点2 二元一次方程的解适合二元一次方程的一对未知数的值叫做这个二元一次方程的一个解. 如83x y ==,是方程231035x y ++=的一个解,记作83x y =⎧⎨=⎩. 【典例】1.已知关于x y 、的二元一次方程34280x y mx m -+++=,当12x y =-⎧⎨=⎩时,_____m =;若无论m 取任何实数,该二元一次方程都有一个固定的解,则这个固定的解为________.【答案】3;212x y =-⎧⎪⎨=⎪⎩ 【解析】解:把12x y =-⎧⎨=⎩代入方程得:38280m m ---++=,解得:3m =;方程整理得:34(2)80x y m x -+++=, 令20x +=,得到2x =- ,把2x =-代入方程得:6480y --+=, 解得:y=,则方程固定的解为212x y =-⎧⎪⎨=⎪⎩.故答案为:3;212 xy=-⎧⎪⎨=⎪⎩【方法总结】1、根据二元一次方程的解,求字母参数的取值,只需把它的解代入方程中,建立关于参数的方程,解方程即可求出参数的值.2、已知方程的解与某个字母参数的取值无关时,只需要对这个方程进行化简,把含字母参数的项进行合并,并令合并后的字母参数的系数为0,即可求得字母参数的值.【随堂练习】1.(2019春•雨花区校级期末)已知12xy=⎧⎨=⎩是方程7x ay+=的一个解,则a的值是()A.3B.1C.3-D.1-【解答】解:12xy=⎧⎨=⎩是方程7x ay+=的一个解,127a∴+=,解得:3a=.故选:A.2.(2019春•海淀区校级期末)若21xy=⎧⎨=-⎩是二元一次方程9y kx=-的一个解,则k的值为()A.3-B.3C.4-D.4【解答】解:21xy=⎧⎨=-⎩是二元一次方程9y kx=-的一个解,129k∴-=-,解得:4k=.故选:D.3.(2019春•通州区期末)已知关于x,y的二元一次方程23x y t-=,其取值如下表,则p 的值为()A .9B .11C .13D .15【解答】解:由表格可得235m n -=. 则2(2)3(2)m n p +--=, 整理得2310m n p -=-. 所以105p -=,解得15p =. 故选:D .4.(2019春•永州期末)下列选项不是方程25x y -=的解的是( ) A .43x y =⎧⎨=⎩B .21x y =⎧⎨=-⎩C .31x y =⎧⎨=-⎩D .31x y =⎧⎨=⎩【解答】解:A 、将4x =,3y =代入25x y -=的左边得:835-=,右边为5,左边=右边,不合题意;B 、将2x =,1y =-代入25x y -=的左边得:4(1)5--=,右边为5,左边=右边,不合题意;C 、将3x =,1y =-代入25x y -=的左边得:617+=,右边为5,左边≠右边,符合题意; D 、将3x =,1y =代入25x y -=的左边得:615-=,右边为5,左边=右边,不合题意;故选:C .5.(2019春•江汉区期末)若01x y =⎧⎨=⎩和11x y =-⎧⎨=-⎩是方程y kx b =+的解,则k ,b 的值分别是()A .2k =,1b =-B .2k =,1b =C .12k =,1b =- D .12k =,1b = 【解答】解:把01x y =⎧⎨=⎩和11x y =-⎧⎨=-⎩代入方程y kx b =+中得:11b k b =⎧⎨-+=-⎩,解得:21k b =⎧⎨=⎩.故选:B .6.(2019春•余姚市期末)下列各组数中,是二元一次方程231x y -=的解的是( ) A .11x y =⎧⎨=⎩B .11x y =-⎧⎨=-⎩C .11x y =-⎧⎨=⎩D .11x y =⎧⎨=-⎩【解答】解:A、把11xy=⎧⎨=⎩代入方程231x y-=得:左边1=-,右边1=,左边≠右边,所以不是方程231x y-=的解,故本选项不符合题意;B、把11xy=-⎧⎨=-⎩代入方程231x y-=得:左边1=,右边1=,左边=右边,所以是方程231x y-=的解,故本选项符合题意;C、把11xy=-⎧⎨=⎩代入方程231x y-=得:左边5=-,右边1=,左边≠右边,所以不是方程231x y-=的解,故本选项不符合题意;D、把11xy=⎧⎨=-⎩代入方程231x y-=得:左边5=,右边1=,左边≠右边,所以不是方程231x y-=的解,故本选项不符合题意;故选:B.7.(2019春•泰山区期中)下列数值是二元一次方程3224x y+=的解的是()A.29xy=-⎧⎨=⎩B.21xy=⎧⎨=⎩C.89xy=⎧⎨=⎩D.46xy=⎧⎨=⎩【解答】解:把46xy=⎧⎨=⎩代入二元一次方程3224x y+=,可得左边=右边.故选:D.8.(2019春•阳谷县期中)已知二元一次方程5(1)70x k y+--=的一个解是13xy=⎧⎨=-⎩,求k的值( ) A .13B .13-C .53D .53-【解答】解:二元一次方程5(1)70x k y +--=的一个解是13x y =⎧⎨=-⎩,513(1)70k ∴⨯---=, 解得:53k =.故选:C .9.(2019春•惠阳区期末)若12x y =⎧⎨=-⎩是关于x 和y 的二元一次方程1ax y +=的解,则a 的值等于( ) A .1-B .3-C .1D .3【解答】解:把12x y =⎧⎨=-⎩代入方程得:21a -=,解得:3a =, 故选:D .10.(2019春•遵义期末)已知1x =,3y =与1x =-,1y =都是方程y mx n =+的解,则m ,n 的值分别为( )A ..2m =,1n =B ..1m =,2n =C .2m =-,1n =D ..1m =,2n =-【解答】解:根据题意得:31m n m n =+⎧⎨=-+⎩,解得:12m n =⎧⎨=⎩,故选:B .11.(2019春•庐江县期末)下列各组数中,是二元一次方程54x y -=的一个解的是( ) A .13x y =⎧⎨=⎩B .31x y =⎧⎨=⎩C .04x y =⎧⎨=⎩D .26x y =⎧⎨=⎩【解答】解:把选项中四个解逐一代入,得到当2x =时,6y =符合方程54x y -=. 故选:D .二.填空题(共1小题)12.(2019春•和田地区期末)已知21x y =⎧⎨=-⎩是方程26x ky +=的解,则k = 2- .【解答】解:21x y =⎧⎨=-⎩是方程26x ky +=的一个解, ∴代入得:46k -=,解得:2k =-, 故答案为:2-.知识点3解二元一次方程组---代入消元法代入消元法:把方程组的一个方程中的某个未知数用含另一个未知数的代数式表示出来,并代入另一个方程,消去一个未知数,从而把解二元一次方程组转化为解一元一次方程,这种解方程组的方法称为代入消元法,简称代入法.【典例】1.用代入法解方程组(1)2313x y x y -=⎧⎨+=⎩; (2)321235x y x y -=⎧⎨+=⎩.【答案】略 【解析】解:(1)2313x y x y -=⎧⎨+=⎩①②,由②得:3y x =-③,将③代入①得:23(3)1x x --=, 整理得:510x =, 解得:2x =,把2x =代入②得:1y =, 故方程组的解为.(2)321235x y x y -=⎧⎨+=⎩①②由①得,2133x y =+③,把③代入②得,212()3533y y ++=, 解得1y =,把1y =代入③式得,1x =,故方程组的解为11x y =⎧⎨=⎩.【方法总结】用代入消元法解二元一次方程组时,尽量选取一个未知数的系数的绝对值是1的方程进行变形;若未知数的系数的绝对值都不是1,则选取系数的绝对值较小的方程变形.【随堂练习】1.(2018春•资中县期中)解方程组【解答】解:(1),把①代入②,5x ﹣3(3x ﹣2)=﹣2, 解得:x=2,将x=2代入①,得:y=3×2﹣2=4, 所以方程组的解为;知识点4 解二元一次方程组---加减消元法把方程组的两个方程(或先做适当变形)相加或相减,消去其中一个未知数,从而把解二元一次方程组转化为解一元一次方程,这种解方程组的方法称为加减消元法,简称加减法.【典例】1.用加减消元法解下列二元一次方程组(1){2x +3(y −2)=6x −y 2=2;(2){7x +4y =2①3x −6y =24②. 【答案】略.【解析】解:(1)方程组整理得:{2x +3y =12①2x −y =4②,①﹣②得:48y =, 解得:2y =,把2y =代入①得:3x =, 则方程组的解为{x =3y =2.(2)①×3+②×2得:2754x = , 解得:2x =,把2x =代入①得:3y =-, 则方程组的解为{x =2y =−3.【方法总结】先将给出的二元一次方程组进行适当变形,再利用加减消元法进行求解,它的使用场景如下: 1.当两个二元一次方程中同一个未知数的系数相等时,把两个方程的两边分别相相减; 2.当两个二元一次方程中同一个未知数的系数相反时,把两个方程的两边分别相加. 3.当两个二元一次方程中同一个未知数的系数均不相等或互为相反数时,可以找其中一个相同未知数系数的最小公倍数,将它们通过变形,把系数变为相同或相反.【随堂练习】1.(2018•宿迁)解方程组:.【解答】解:,①×2﹣②得: ﹣x=﹣6, 解得:x=6, 故6+2y=0, 解得:y=﹣3, 故方程组的解为:.2.(2018•湘西州)解方程组:【解答】解:①+②得:4x=8, 解得:x=2,把x=2代入①得:2+y=3, 解得:y=1,所以原方程组的解为.【补充练习】1.(2019春•来宾期末)方程组3452410x y x y +=⎧⎨-=⎩的解是( )A .31x y =⎧⎨=-⎩B .21x y =⎧⎨=-⎩C .12x y =-⎧⎨=⎩D .21x y =⎧⎨=⎩【解答】解:原方程组的两个方程相加可得515x =,解得3x =,把3x =代入第一个方程可得1y =-. 故选:A .2.(2019春•谢家集区期末)小丽在用“加减消元法”解二元一次方程组524239x y x y -=⎧⎨+=⎩①②时,利用①a ⨯+②b ⨯消去x ,则a 、b 的值可能是( ) A .2a =,5b =B .3a =,2b =C .3a =-,2b =D .2a =,5b =-【解答】解:小丽在用“加减消元法”解二元一次方程组524239x y x y -=⎧⎨+=⎩①②时,利用①a ⨯+②b ⨯消去x ,则a 、b 的值可能是2a =,5b =-, 故选:D .3.(2019春•云梦县期末)方程组4(2)5123(2)3x y x y ++=⎧⎨++=⎩的解是( )A .31x y =⎧⎨=⎩B .31x y =⎧⎨=-⎩C .31x y =-⎧⎨=-⎩D .31x y =-⎧⎨=⎩【解答】解:方程组整理得:457233x y x y +=-⎧⎨+=-⎩①②,②2⨯-①得:1y =, 把1y =代入②得:3x =-, 则方程组的解为31x y =-⎧⎨=⎩.4.(2019•孝感)已知二元一次方程组1249x y x y +=⎧⎨+=⎩,则22222x xy y x y -+-的值是( ) A .5- B .5 C .6- D .6【解答】解:1249x y x y +=⎧⎨+=⎩①②,②-①2⨯得,27y =,解得72x =, 把72x =代入①得,712y +=,解得52y =-, ∴22222752()226()()1x xy y x y x y x y x y x y x y +-+--====-+-+. 故选:D .5.(2019•从化区一模)已知326a b a b -=⎧⎨-=⎩,则a b +等于( )A .1B .3C .1-D .3-【解答】解:326a b a b -=⎧⎨-=⎩①②,②-①得:3a =, 把3a =代入①得:0b =, 则3a b +=, 故选:B .6.(2019春•莒县期中)若|321|0x y --=,则点(,)x y 在第( )象限. A .四B .三C .二D .一【解答】解:|321|0x y --, ∴3212x y x y -=⎧⎨+=⎩,解得:11x y =⎧⎨=⎩,则点(1,1)在第一象限,7.(2019•鞍山一模)若|2|0x y--=,则x,y的值为()A.31xy=⎧⎨=⎩B.13xy=⎧⎨=⎩C.2xy=⎧⎨=⎩D.31xy=⎧⎨=-⎩【解答】解:|2|0x y--=,∴24x yx y-=⎧⎨+=⎩①②,①+②得:26x=,解得:3x=,②-①得:22y=,解得:1y=,则方程组的解为31xy=⎧⎨=⎩,故选:A.8.(2019春•冠县期中)解方程组①3759y xx y=-⎧⎨+=-⎩,②35123156x yx y+=⎧⎨-=-⎩,比较简便的方法是()A.都用代入法B.都用加减法C.①用代入法,②用加减法D.①用加减法,②用代入法【解答】解:①中的第一个方程为2y x=-,用代入法比较简便;②中的x的系数相等,用加减法比较简便;故选:C.9.(2019•贵阳模拟)若关于x,y的二元一次方程组2132x yx y+=⎧⎨-+=⎩的解为x ay b=⎧⎨=⎩,则4a b+的值为()A.17B.197C.1D.3【解答】解:2132x yx y+=⎧⎨-+=⎩①②,把③代入②得,3(12)2x x -+-=,解得17x =, 把17x =代入③得,25177y =-=, ∴1757a b ⎧=⎪⎪⎨⎪=⎪⎩,1544377a b ∴+=+⨯=. 故选:D .10.(2018秋•兰州期末)如果方程组4x y mx y m +=⎧⎨-=⎩的解是二元一次方程35300x y --=的一个解,那么m 的值为( ) A .7B .6C .3D .2【解答】解:4x y m x y m +=⎧⎨-=⎩①②,①+②得:25x m =, 解得: 2.5x m =, ①-②得:23y m =-, 解得: 1.5y m =-,代入35300x y --=得:7.57.5300m m +-=, 解得:2m =, 故选:D .二.解答题(共1小题)11.(2019春•海淀区校级期末)解关于x 、y 的二元一次方程组: (1)136224x y x y ⎧+=-⎪⎨⎪+=⎩(2)258325x y a x y a +=⎧⎨+=⎩【解答】解:(1)136224x y x y ⎧+=-⎪⎨⎪+=⎩①②,把③代入①,得1(42)362y y -+=-,解得4y =-,把4y =-代入③中得12x =. 所以原方程的解为124x y =⎧⎨=-⎩.(2)258325x y a x y a +=⎧⎨+=⎩①②,①3⨯-②2⨯,得1114y a =, 所以1411ay =, ②5⨯-①2⨯,得119x a =, 所以911a x =. 所以原方程的解为9111411a x a y ⎧=⎪⎪⎨⎪=⎪⎩.知识点5 二元一次方程组的解的概念二元一次方程组中两个方程的公共解叫做二元一次方程组的解.【典例】1.已知方程组40ax by ax by -=⎧⎨+=⎩ 的解为21x y =⎧⎨=⎩,则23a b +的值为________.【答案】﹣4 【解析】解:∵方程组40ax by ax by -=⎧⎨+=⎩的解为21x y =⎧⎨=⎩,∴把21x y =⎧⎨=⎩代入方程组中得2420a b a b -=⎧⎨+=⎩,解得12a b =⎧⎨=-⎩,∴23213(2)264a b +=⨯+⨯-=-=-. 故答案为:-4.【方法总结】已知二元一次方程组的解,求参数或某些含参代数式的值,只需把它的解代入方程组中,得到关于参数的新方程组,解这个新方程组,求出参数的值,进而求得含参代数式的值.【随堂练习】1.(2018春•白云区期末)下列方程组中,是二元一次方程组的是( ) A .B .C .D .【解答】解:A 、未知数的次数是2,错误; B 、含有三个未知数,错误; C 、不是整式方程组,错误;D 、符合二元一次方程组的定义,正确; 故选:D .知识点6 同解方程组 【典例】1.(1)已知方程组2524x y ax by +=⎧⎨-=-⎩和方程组3208x y bx ay -=⎧⎨+=⎩的解相同,求2010(2)a b +的值.(2)甲、乙两人共同解方程组51542ax y x by +=⎧⎨-=-⎩①② ,由于甲看错了方程①中的a ,得到方程组的解为31x y =-⎧⎨=-⎩;乙看错了方程②中的b ,得到方程组的解为54x y =⎧⎨=⎩.试计算:201320121()10ab +.【答案】略【解析】解:(1)∵方程组2524x y ax by +=⎧⎨-=-⎩和方程组3208x y bx ay -=⎧⎨+=⎩的解相同,∴方程组2+52320x y x y =⎧⎨-=⎩与上述两方程组有相同的解.解可得62x y =⎧⎨=-⎩.将其代入到48ax by bx ay -=-⎧⎨+=⎩中,化简得624628a b b a +=-⎧⎨-=⎩,解得11a b =-⎧⎨=⎩.∴20102010(2)(1)1a b +=-=.(2)甲看错了方程①中的a ,则31x y =-⎧⎨=-⎩满足方程组②, 把31x y =-⎧⎨=-⎩代入②得:122b -+=-,即10b =;乙看错了方程②中的b ,则54x y =⎧⎨=⎩满足方程组①,把54x y =⎧⎨=⎩代入①得:52015a +=,即1a =-,则201320121()10ab +201320121(1)(10)10110=-+⨯=-+=【方法总结】1.已知两个含参方程组的解相同,只需把它们之中不含参的方程组成新的方程组,解方程组,求得它们共有的解,再将它们分别代入含参的方程中,求得参数的值.2.关于看错字母问题,只需把所得的解代入未看错的方程中,分别求解即可.【随堂练习】1.(2017秋•雁塔区校级期末)已知方程组与有相同的解,则m=____,n=___. 【解答】解:由(1)×2+(2),得10x=20, x=2,代入,得y=0.将x 、y 代入第一个方程组可得,解,得.知识点7 解三元一次方程组1、一般地,由几个一次方程组成,并且含有三个未知数的方程组,叫做三元一次方程组.2、解三元一次方程组的基本思想是消元,即应用代入法或加减法消去一个未知数,从而变三元为二元,然后解这个二元一次方程组,求出两个未知数,最后再求出另一个未知数.【典例1】1.解三元一次方程组.【答案】略【解析】解:①×2﹣②,得57y z -=④①×3-③,得53y z +=⑤④+⑤,得1y =.将1y =代入⑤,得2z =-.将12y z ==,﹣代入①,得7x =.故原方程组的解是.【方法总结】解三元一次方程组的基本方法是代入法和加减法,加减法比较常用,我们一定要根据方程组的特点,选准消元对象,定好消元方案.例如:当三个方程中有一个方程是二元一次方程,则可以先通过对另外两个方程组进行消元,消元时就消去三个元中缺少的那个元,即“缺某元,消某元”.2.若2x ﹣3y+z=0,3x ﹣2y ﹣6z=0,且xyz≠0,求的值.【答案】略 【解析】解:由题意得:,②×3﹣①×2,得:5x=20z ,即x=4z ,将x=4z 代入①,得:8z ﹣3y=﹣z ,解得y=3z , 将x=4z 、y=3z 代入原式,得: 原式===.【方法总结】已知两个一次方程,含有三个未知数(如:x y z ,, ),求关于这三个未知数的代数式的值,只需把其中一个未知数(如:z )当作一个常数,解关于另外两个未知数(如:x y , )的二元一次方程组,将求得的解代入代数式中,即可求得代数式的值.【随堂练习】1.(2019春•武昌区期中)在等式2y ax bx c =++中,当0x =时,2y =;当1x =-时,0y =;当2x =时,12y =,则(a b c ++= ) A .4B .5C .6D .8【解答】解:把0x =时,2y =;1x =-时,0y =;2x =时,12y =分别代入2y ax bx c =++,得201242c a b ca b c =⎧⎪=-+⎨⎪=++⎩, 解得,132a b c =⎧⎪=⎨⎪=⎩,1326a b c ∴++=++=,故选:C .2.(2019春•南江县期末)下列四组数值中,为方程组202132x y z x y z x y z ++=⎧⎪--=⎨⎪--=⎩的解是( )A .012x y z =⎧⎪=⎨⎪=-⎩B .101x y z =⎧⎪=⎨⎪=⎩C .010x y z =⎧⎪=-⎨⎪=⎩D .123x y z =⎧⎪=-⎨⎪=⎩【解答】解:202132x y z x y z x y z ++=⎧⎪--=⎨⎪--=⎩①②②,①+②得:31x y +=④, ①+③得:42x y +=⑤, ⑤-④得:1x =, 将1x =代入④得:2y =-, 将1x =,2y =-代入①得:3z =, 则方程组的解为123x y z =⎧⎪=-⎨⎪=⎩.故选:D .3.(2019春•莘县期中)关于x ,y 的方程组232(1)10x y kx k y -=⎧⎨++=⎩的解互为相反数,则k 的值是( ) A .8B .9C .10D .11【解答】解:由x ,y 互为相反数得x y =-,代入(1)得1y=-,则1x=,把1x=,1y=-,代入(2)得:2110k k--=,则11k=.故选:D.4.(2018•丰润区一模)已知3243x y kx y k+=⎧⎨-=+⎩,如果x与y互为相反数,那么()A.0k=B.34k=-C.32k=-D.34k=【解答】解:已知3243x y kx y k+=⎧⎨-=+⎩,解得9651195kxky+⎧=⎪⎪⎨+⎪=-⎪⎩,x与y互为相反数,∴961190 55k k++-=,即32k=-.故选:C.二.填空题(共4小题)5.(2018秋•九龙坡区校级期末)育德文具厂生产的一种文具套装深受学生喜爱,已知该文具套装一套包含有1个笔袋,2只笔,3个笔记本,巅峰文具超市向该厂订购了一批文具套装,需要厂家在15天内生产完该套装并交货.育德文具厂将员工分为A、B、C三个组,分别生产笔袋、笔、笔记本,他们于某天零点开始工作,每天24小时轮班连续工作(假设每小时工作效率相同),若干天后的零点A组完成任务,再过几天后(不少于一天)的中午12点B组完成低务,再过几天(不少于一天)后的6时C组完成任务.已知A、B、C三个组每天完成的任务数分别是270个、360个、360个,则巅峰文具超市一共订购了1350套文具套装.【解答】解:设A组工作x天,B组工作1()2x m++天,C组工作11()24x m n++++天,(x,m ,n 都是正整数,且1m ,1)n ,则15x m n ++<,根据题意得,13602270211360327024x m x x m n x ⎧⎛⎫++=⨯ ⎪⎪⎪⎝⎭⎨⎛⎫⎪++++=⨯ ⎪⎪⎝⎭⎩①②由①得,21x m =+③, 由②得,5443x m n =++④, ④5-⨯③得,312m n +=, m ,n 是正整数,∴当1m =时,2n =,5x =,8m n x ∴++=,符合题意,当3m =时,5n =,7x =, 15m n x ∴++=,不符合题意,即:A 组工作5天,∴一共加个了27051350⨯=个笔袋,∴巅峰文具超市一共订购了1350套文具套装,故答案为:1350.6.(2019春•大丰区期中)若5a b b c a c +=+=+=,则a b c ++= 152. 【解答】解:根据题意得5a b +=,5b c +=,5a c +=, 三个式子左右两边分别相加得2()15a b c ++=, 则152a b c ++=. 故答案是:152. 7.(2019春•洛江区期末)三元一次方程组598x y y z z x +=⎧⎪+=⎨⎪+=⎩的解是236x y z =⎧⎪=⎨⎪=⎩. 【解答】解:598x y y z z x +=⎧⎪+=⎨⎪+=⎩①②③,①+②+③得:2()22x y z ++=,即11x y z ++=④, 将①代入④得:6z =,将②代入④得:2x =, 将③代入④得:3y =, 则方程组的解为236x y z =⎧⎪=⎨⎪=⎩.故答案为:236x y z =⎧⎪=⎨⎪=⎩8.(2019春•雨花区期末)已知:357a b c==,且3249a b c +-=,则a b c ++的值等于 15- .【解答】解:设357a b ck ===, 则3a k =,5b k =,7c k =, 代入3249a b c +-=, 得910289k k k +-=, 解得:1k =-,3a ∴=-,5b =-,7c =-,于是35715a b c ++=---=-. 故本题答案为:15-. 三.解答题(共1小题)9.(2019春•武昌区期中)解方程组3232443210x y z x y z x y z -+=⎧⎪+-=⎨⎪++=-⎩.【解答】解:3232443210x y z x y z x y z -+=⎧⎪+-=⎨⎪++=-⎩①②③,①+②得:57x y -=④; ②2⨯+③得:852x y +=-⑤, ④5⨯+⑤得:3333x =,即1x =, 把1x =代入④得:2y =-, 把1x =,2y =-代入①得:4z =-,则方程组的解为124x y z =⎧⎪=-⎨⎪=-⎩.综合运用1.关于x y ,的方程组的解是,其中y 的值被盖住了,不过仍能求出p ,则p 的值是____【答案】﹣【解析】解:根据题意,将1x = 代入3x y +=,可得2y =,将12x y ==,代入0x py +=,得:120p +=, 解得:12p =-.2.已知是方程组的解,则3_____m n +=.【答案】7 【解析】解:∵是方程组的解,∴把代入得:,解得:14m n =⎧⎨=⎩ .∴33147m n +=⨯+=, 故答案为:7. 3.已知方程326m n xy --+=是二元一次方程,则_____m n -=.【答案】3【解析】解:由题意得:31m -=,21n -=, 解得:41m n ==,,413m n -=-=,故答案为:3.4.解方程组1312428x y x y ⎧-+=⎪⎨⎪-+=-⎩.【答案】略.【解析】解:方程组化简,得 {−2x +3y =4①y =−8+2x②,把②代入①,得23(82)4x x -+-+=,解得7x =, 把7x =代入②,得8276y =-+⨯=,方程组的解是{x =7y =6.5.用加减消元法解二元一次方程组{3(x −1)=y +55y −6=3(x +4).【答案】略【解析】解:方程组整理得:{3x −y =8①3x −5y =−18②,①﹣②得:4y=26, 解得:132y =, 把132y =代入①得:296x =, 则方程组的解为296132x y ⎧=⎪⎨⎪=⎩.6.已知方程组和有相同的解,求222a ab b +-的值.【答案】略 【解析】解:解方程组得, 把代入第二个方程组得,解得,则22222()(21)1a ab b a b +=-=-=-.7.甲、乙两人共同解方程组由于甲同学看错了方程①中的a ,得到方程组的解为434x y =-⎧⎪⎨=-⎪⎩,乙看错了方程②中的b ,得到方程组的解为59x y =⎧⎨=-⎩.请计算代数式20072008a b 的值. 【答案】略【解析】解:由甲同学看错了方程①中的a 可知,434x y =-⎧⎪⎨=-⎪⎩满足方程组②, 把434x y =-⎧⎪⎨=-⎪⎩代入②得,344()=14b -+⨯-,解得1b =-. 由乙看错了方程②中的b 可知,59x y =⎧⎨=-⎩满足方程组①,把59x y =⎧⎨=-⎩代入①得,55916a ⨯+=,解得1a =-.∴20072008a b=(﹣1)2007×(﹣1)2008=(﹣1)4015=﹣1.8.解方程组:{3x −y +z =10①x +2y −z =6②x +y +2z =17③.【答案】略.【解析】解:①+②得:4x+y=16④, ②×2+③得:3x+5y=29⑤, ④⑤组成方程组{4x +y =163x +5y =29解得{x =3y =4将x=3,y=4代入③得:z=5, 则方程组的解为{x =3y =4z =5.9.已知:4360270x y z x y z --=+-=,,求23657x y zx y z++++的值.【答案】略.【解析】解:由题意得{4x −3y −6z =0①x +2y −7z =0②,①﹣②×4得:11220y z -+=,解得:2y z =,将2y z =代入①得:3x z =, 即{x =3z y =2z, 把{x =3zy =2z 代入23657x y z x y z++++中 原式= 6669=310710z z z z z z ++++.。


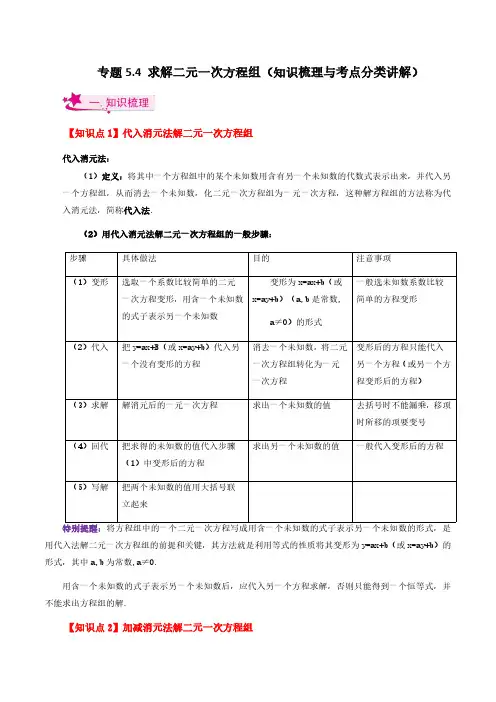
专题5.4求解二元一次方程组(知识梳理与考点分类讲解)【知识点1】代入消元法解二元一次方程组代入消元法:(1)定义:将其中一个方程组中的某个未知数用含有另一个未知数的代数式表示出来,并代入另一个方程组,从而消去一个未知数,化二元一次方程组为一元一次方程,这种解方程组的方法称为代入消元法,简称代入法.(2)用代入消元法解二元一次方程组的一般步骤:步骤具体做法目的注意事项(1)变形选取一个系数比较简单的二元一次方程变形,用含一个未知数的式子表示另一个未知数变形为x=ax+b(或x=ay+b)(a,b 是常数,a≠0)的形式一般选未知数系数比较简单的方程变形(2)代入把y=ax+B(或x=ay+b)代入另一个没有变形的方程消去一个未知数,将二元一次方程组转化为一元一次方程变形后的方程只能代入另一个方程(或另一个方程变形后的方程)(3)求解解消元后的一元一次方程求出一个未知数的值去括号时不能漏乘,移项时所移的项要变号(4)回代把求得的未知数的值代入步骤(1)中变形后的方程求出另一个未知数的值一般代入变形后的方程(5)写解把两个未知数的值用大括号联立起来特别提醒:将方程组中的一个二元一次方程写成用含一个未知数的式子表示另一个未知数的形式,是用代入法解二元一次方程组的前提和关键,其方法就是利用等式的性质将其变形为y=ax+b(或x=ay+b)的形式,其中a,b 为常数,a≠0.用含一个未知数的式子表示另一个未知数后,应代入另一个方程求解,否则只能得到一个恒等式,并不能求出方程组的解.【知识点2】加减消元法解二元一次方程组1.加减消元法的定义通过将两个方程相加(减)消去其中一个未知数,将二元一次方程组转化为一元一次方程来解,这种解二元一次方程组的方法叫做加减消元法,简称加减法.2.用加减消元法解二元一次方程组的一般步骤步骤具体做法目的注意事项(1)变形根据绝对值较小的未知数(同一个未知数)的系数的最小公倍数,给方程的两边都乘适当的数.使某一个未知数在两个方程中的系数相等或互为相反数.给某个方程乘一个数时,方程两边的每一项都要和这个数相乘(2)代入两个方程中同一个未知数的系数互为相反数时,将两个方程相加;同一个未知数的系数相等时,将两个方程相减.消去一个未知数,将二元一次方程组转化为一元一次方程把两个方程相加(减)时,一定要把两个方程两边分别相加(减).(3)求解解消元后的一元一次方程求出一个未知数的值(4)回代把求得的未知数的值代入方程组中某个较简单的方程求出另一个未知数的值回代时选择系数较简单的方程(5)写解把两个未知数的值用大括号联立起来特别提醒:1.两个方程同一未知数的系数的绝对值相等或成倍数关系时,解方程组应考虑用加减消元法.2.如果同一未知数的系数的绝对值既不相等又不成倍数关系,我们应设法将一个未知数的系数的绝对值转化为相等关系.3.用加减法时,一般选择系数比较简单(同一未知数的系数的绝对值相等或成倍数关系)的未知数作为消元对象.【考点目录】【考点1】代入消元法解二元一次方程组;【考点2】加减消元法解二元一次方程组;【考点3】同解方程组;【考点4】整体思想解二元一次方程组;【考点5】求解二元一次方程组——错题复原问题;【考点6】求解二元一次方程组——参数问题;【考点7】构造二元一次方程组求解。



北师大版数学八年级上册2《求解二元一次方程组》教案1一. 教材分析《求解二元一次方程组》是人教版初中数学八年级上册的一章内容。
这一章主要让学生掌握二元一次方程组的解法,以及应用方程组解决实际问题。
此章节在数学知识体系中起着承前启后的作用,为后续学习更复杂的方程组和函数打下基础。
二. 学情分析学生在学习本章内容前,已经掌握了方程和一元一次方程的解法,但对于二元一次方程组,他们可能还缺乏直观的认识和解决方法。
因此,在教学过程中,需要引导学生从实际问题中抽象出二元一次方程组,并通过实例让学生感受方程组的意义和应用。
三. 教学目标1.理解二元一次方程组的含义,掌握二元一次方程组的解法。
2.能够应用二元一次方程组解决实际问题。
3.培养学生的抽象思维能力和解决问题的能力。
四. 教学重难点1.重点:二元一次方程组的解法及应用。
2.难点:如何引导学生从实际问题中抽象出二元一次方程组,以及解二元一次方程组的方法。
五. 教学方法1.采用问题驱动的教学方法,引导学生从实际问题中提出问题,并探索解决问题的方法。
2.使用多媒体教学,通过动画和实例,帮助学生直观地理解二元一次方程组的概念和解法。
3.学生进行小组讨论和合作交流,培养学生的团队协作能力。
六. 教学准备1.多媒体教学设备。
2.教学课件和教学素材。
3.练习题和实际问题。
七. 教学过程1.导入(5分钟)通过一个实际问题,引导学生提出二元一次方程组的问题,激发学生的学习兴趣。
2.呈现(10分钟)介绍二元一次方程组的概念,并通过多媒体展示实例,让学生直观地理解二元一次方程组的意义。
3.操练(10分钟)引导学生通过小组讨论,探索解二元一次方程组的方法。
教师在旁边给予指导,并引导学生总结解法。
4.巩固(10分钟)让学生独立解决一些简单的二元一次方程组问题,检验学生对解法的掌握情况。
5.拓展(10分钟)引导学生思考如何应用二元一次方程组解决实际问题,并让学生举例说明。
6.小结(5分钟)教师引导学生总结本节课所学内容,强调二元一次方程组的概念和解法。

北师大版数学八年级上册2《求解二元一次方程组》说课稿1一. 教材分析《求解二元一次方程组》是人教版初中数学八年级上册第二章《二元一次方程组》的一部分。
这部分内容是在学生已经掌握了二元一次方程、一元一次方程的解法的基础上进行学习的。
通过这部分的学习,使学生能够掌握二元一次方程组的解法,并能够应用到实际问题中。
本节课的主要内容有:二元一次方程组的定义、二元一次方程组的解法(代入法、加减法)、二元一次方程组的应用。
在教材的安排上,首先是引导学生通过实际问题抽象出二元一次方程组,然后通过合作交流,探索二元一次方程组的解法,最后通过应用题,巩固二元一次方程组的解法。
二. 学情分析八年级的学生已经具备了一定的数学基础,对一元一次方程的解法有一定的了解。
但是,对于二元一次方程组,学生还比较陌生,需要通过实例来引导学生理解。
在学生的学习过程中,我发现学生对于数学问题的生活情境比较感兴趣,因此,我在教学过程中,会尽量结合生活实例,激发学生的学习兴趣。
三. 说教学目标1.知识与技能目标:理解二元一次方程组的定义,掌握二元一次方程组的解法(代入法、加减法),能够应用到实际问题中。
2.过程与方法目标:通过合作交流,探索二元一次方程组的解法,提高学生的合作交流能力。
3.情感态度与价值观目标:培养学生对数学的兴趣,增强学生的自信心。
四. 说教学重难点1.教学重点:二元一次方程组的解法(代入法、加减法)。
2.教学难点:如何引导学生理解二元一次方程组的解法,并能够应用到实际问题中。
五. 说教学方法与手段1.教学方法:采用启发式教学法、合作交流法、实例教学法。
2.教学手段:利用多媒体课件,帮助学生直观地理解二元一次方程组的概念和解法。
六. 说教学过程1.导入:通过一个实际问题,引导学生抽象出二元一次方程组,激发学生的学习兴趣。
2.探究:让学生通过合作交流,探索二元一次方程组的解法,教师给予适当的引导和点拨。
3.讲解:教师讲解二元一次方程组的解法(代入法、加减法),并通过实例进行说明。

北师大初二数学8年级上册秋季版(学生版)最新讲义第11讲二元一次方程组的应用知识点1 配套问题在配套问题中,已知a件甲商品和b件乙商品恰好配成一套,即一套中甲乙的数量比是a:b,要使生产出的产品配套,就得满足甲乙的总数量之比也为a:b.【典例】1.机械厂加工车间有85名工人,平均每人每天加工大齿轮16个或小齿轮10个,2个大齿轮和3个小齿轮配成一套,问需分别安排多少名工人加工大、小齿轮,才能使每天加工的大小齿轮刚好配套?【随堂练习】1.(2018•深圳模拟)玩具车间每天能生产甲种玩具零件24个或乙种玩具零件12个,若甲种玩具零件一个与乙种玩具零件2个能组成一个完整的玩具,怎样安排生产才能在60天内组装出最多的玩具设生产甲种玩具零件x天,乙种玩具零件y天,则有()A.B.C.D.2.(2016春•嵊州市校级月考)某车间有28名工人生产螺栓和螺母,每人每小时平均能生产螺栓12个或螺母18个,一个螺栓配两个螺母,应分配____人生产螺栓,____人生产螺母,才能使生产的螺栓和螺母正好配套.知识点2 行程问题一、路程=速度×时间二、设甲、乙两人相距一定距离.1.相遇问题---甲、乙两人相向而行后相遇:甲、乙两人之间的初始距离=甲所走的路程+乙所走的路程.2.追及问题---甲、乙同向而行后相遇:①同时不同地:速度快的所走路程=速度慢的所走路程+甲乙之间的初始距离;②同地不同时:甲行距离=乙行距离或慢者所用时间=快者所用时间+慢者比快者多用用的时间.三、航行问题1.船:顺水速度=静水速度+水速逆水速度=静水速度-水速.2.飞机:顺风速度=静风速度+风速逆风速度=静风速度-风速.3.静水速度=(顺流速度+逆流速度)÷24.水流速度=(顺流速度-逆流速度)÷2【典例】1.甲、乙两人相距42km,若相向而行,则需2小时相遇,若同向而行,乙要14时才能追上甲,则甲、乙二人每小时各走多少千米?2.两地相距280千米,一艘船在其间航行,顺流航行了14小时,逆流航行了20小时,求这艘轮船在静水中的速度和水的流速?【随堂练习】1.(2018春•丹江口市期中)甲、乙两人练习赛跑,如果甲让乙先跑10米,那么甲跑5秒钟就可以追上乙;如果甲让乙先跑2秒钟,那么甲跑4秒钟就能追上乙,求两人每秒钟各跑多少米?2.(2018春•厦门期中)甲,乙两人相距42千米,两人同时出发相向而行,两小时后相遇;同时出发同向而行,甲14小时可追上乙,求甲,乙两人的速度.知识点3 销售问题单价×数量=总价利润=实际售价-成本实际售价=标价(原价)×折扣=100 利润利润率%成本【典例】1.小林在某商店购买商品A ,B 共三次,只有其中一次购买时,商品A ,B 同时打折,其余两次均按标价购买,三次购买商品A 、B 的数量和费用如表所示,(1)在这三次购物中,第_____次购物打了折扣;(2)求出商品A、B的标价;(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?2.有一商场计划用7万元从厂家购进60台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1100元,乙种每台1300元,丙种每台2100元.(1)若商场同时购进其中两种不同型号的电视机共60台,用去7万元,请你研究一下商场的进货方案.(2)若商场销售一台甲种电视机可获利200元,销售一台乙种电视机可获利300元,销售一台丙种电视机可获利400元,在同时购进两种不同型号电视机方案中,为使销售时获利最多,你选择哪种进货方案?【随堂练习】1.(2018•绥阳县模拟)某种高端品牌的家用电器,若按标价打八折销售该电器一件,则可获利润500元,其利润率为20%.现如果按同一标价打九折销售该电器一件,那么获得的纯利润为()A.562.5元B.875元C.550元D.750元。