最新(高等数学)第四章导数的应用
- 格式:doc
- 大小:459.00 KB
- 文档页数:62

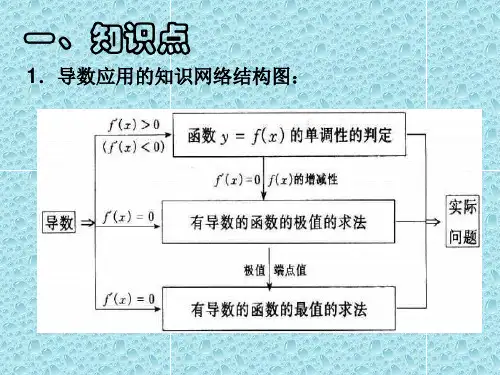
第四章 导数的应用第一节 中值定理一.费马定理1.定义1.极值设函数()x f 在点0x 的某邻域()0U x 内对一切()0x U x ∈有()()0f x f x ≤或(()()0f x f x ≥),则称()x f 在点0x 处取得极大值(或极小值);并称0x 为()x f 的极大值点(或极小值点).注意:极大值、极小值在今后统称为极值;极大值点、极小值点在今后统称为极值点;2.定理1.极值的必要条件(费马定理)设()x f 在点0x 的某邻域()0U x 内有定义,且在0x 处可导,若()0f x 为极值,则必有:()00f x '=.证明:不妨设()0f x 为极大值。
按极大值的定义,则0x ∃的某个邻域,使对一切此邻域内的x 有()()0f x f x ≤--------------(1) 所以,()()()0000lim 0;x x f x f x f x x x --→-'=≥-()()()0000l i m 0;x x f x f x f x x x ++→-'=≤---------(2)又因为()0f x '存在,所以应有()()00f x f x -+''=---------(3) 故,由(2)式及(3)式,必有()00f x '=.1.注意:使()00f x '=的点0x 可能为()x f 的极大值点(或极小值点),也可能不是.比如:20,0.y x x == 二.中值定理1.定理2.罗尔中值定理:若值设函数()x f 满足:(1)()x f 在区间[]b a ,上连续; (2)()x f 在区间()b a ,内可导; (3)()()b f a f =.则,必至少存在一点()b a ,∈ξ,使()0f ξ'=注意:罗尔定理的几何意义是说,在每点处都有非垂直切线的一段曲线上,若两端点处的高度相同,则在曲线上至少存在一条水平切线.(作图说明) 证明:由闭区间上连续函数的性质,()x f 在[]b a ,上有最大值M 及最小值m. (1) 若M=m ,则()M x f ≡,[]b a x ,∈∀.所以,()()0,,.f x x a b '≡∀∈任取()b a ,∈ξ,均满足()0f ξ'=;(2) 若m M ≠,则M 和m 中至少有一个不等于()()b f a f =,因此则M 和m中至少有一个在区间内部某点()b a ,∈ξ处取到.不妨设()ξf 为()x f 的最大值,从而也是极大值。






高等数学中的导数应用导语:高等数学是大学中数学专业的重要基础课程,其中导数是一个关键概念。
导数的应用广泛,涉及到各个领域,如物理学、经济学、工程学等。
本文将从几个方面介绍高等数学中导数的应用,包括极值问题、曲线的切线与法线、微分方程等。
一、极值问题极值问题是导数应用中的经典问题之一。
在实际问题中,我们常常需要求解一个函数的最大值或最小值。
通过求解导数为零的点,我们可以找到函数的极值点。
例如,考虑一个简单的问题:求解函数y=x^2在定义域[0,1]上的最大值。
我们可以通过求解导数dy/dx=2x=0得到极值点x=0。
进一步,我们可以通过求解二阶导数d^2y/dx^2=2来判断这个极值点是最大值还是最小值。
通过这种方法,我们可以解决更加复杂的实际问题,如优化问题、最优控制问题等。
二、曲线的切线与法线导数的另一个重要应用是求解曲线的切线与法线。
在几何学中,我们经常需要确定曲线在某一点的切线和法线。
通过求解导数,我们可以得到曲线在该点的切线斜率,进而确定切线的方程。
例如,考虑函数y=x^3,在点(1,1)处的切线。
我们可以通过求解导数dy/dx=3x^2得到斜率为3的切线。
进一步,我们可以利用切线的斜率和点(1,1)得到切线方程y-1=3(x-1)。
同样的方法也可以用于求解曲线的法线。
三、微分方程微分方程是导数应用的重要领域之一。
微分方程描述了变量之间的关系,通常涉及到导数。
通过求解微分方程,我们可以得到函数的解析解或数值解。
微分方程的应用广泛,如物理学中的运动学问题、生物学中的人口增长模型等。
例如,考虑一个简单的一阶线性微分方程dy/dx=kx,其中k为常数。
通过求解这个微分方程,我们可以得到函数y=kx^2/2+C,其中C为常数。
通过这种方法,我们可以解决更加复杂的微分方程问题,如二阶微分方程、偏微分方程等。
四、导数在实际问题中的应用导数在实际问题中的应用非常广泛。
例如,在物理学中,我们可以利用导数来描述物体的运动状态,如速度、加速度等。


第四章微分中值定理和导数的应用一、考核要求Ⅰ 知道罗尔定理成立的条件和结论,知道拉格朗日中值定理成立的条件和结论。
Ⅱ 能识别各种类型的未定式,并会用洛必达法则求它们的极限。
Ⅲ 会判别函数的单调性,会用单调性求函数的单调区间,并会利用函数的单调性证明简单的不等式。
Ⅳ 会求函数的极值。
Ⅴ 会求出数在闭区间上的最值,并会求简单应用问题的最值。
Ⅵ 会判断曲线的凹凸性,会求曲线的凹凸区间和拐点。
Ⅶ 会求曲线的水平渐近线和垂直渐近线。
二、基本概念、主要定理和公式、典型例题Ⅰ 微分中值定理今后,如果函数f(x)在某一点x0处的导数值=0,就说这一点是驻点,因此罗尔中值定理的结论也可以说f(x)在(a,b)内至少有一个驻点。
从y=f(x)的几何图形(见下图)可以看出,若y=f(x)满足罗尔中值的条件,则它在(a,b)内至少有一点,其切线是水平的,根据导数的几何意义知道,该点的斜率=k=0。
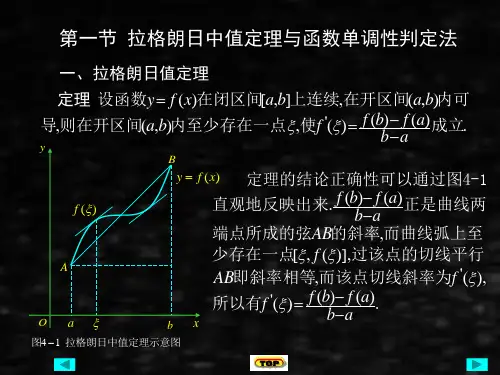
从函数y= f(x)的图形看(见下图),连接y= f(x)在[a,b]上的图形的端点A与B,则线段AB的斜率为:将AB平行移动至某处,当AB的平行线与曲线y=f(x)相切时,若切点为x=c,则根据导数的几何意义知:或写作故从几何图形看,拉格朗日定理是成立的。
典型例题例一:(单选)下列函数在相应区间上满足罗尔中值定理的条件的函数是()① ,[-1,1];② ,[-1,1];③ ,[1, 2];④ ,[-1,1]。
解:①在[-1,1]上处处有意义,没有无意义的点,因为他没有分母,所以在b区间[-1,1]上处处连续满足第一个条件。
又f(-1)=1,f(1)=1,所以在端点上函数值相等,满足第三个条件因此这函数在开间内不是处处可导,只少在0这一点不可导的,因此不满足第二个条件。
② 在x=o处不可导,∴也不满足第二个条件。
③ f(1)=1,f(2)=4,∴在[1,2]上满足第三个条件。
④ ,处处可导且处处连续,f(-1)=1, f(1)=1。
(高等数学)第四章导数的应用第四章导数的应用第一节中值定理一.费马定理1.定义1.极值设函数«Skip Record If...»在点«Skip Record If...»的某邻域«Skip Record If...»内对一切«Skip Record If...»有«Skip Record If...»或(«Skip Record If...»),则称«Skip Record If...»在点«Skip Record If...»处取得极大值(或极小值);并称«Skip Record If...»为«Skip Record If...»的极大值点(或极小值点).注意:极大值、极小值在今后统称为极值;极大值点、极小值点在今后统称为极值点;2.定理1.极值的必要条件(费马定理)设«Skip Record If...»在点«Skip Record If...»的某邻域«Skip Record If...»内有定义,且在«Skip Record If...»处可导,若«Skip Record If...»为极值,则必有:«Skip Record If...».证明:不妨设«Skip Record If...»为极大值。
按极大值的定义,则«Skip Record If...»的某个邻域,使对一切此邻域内的«Skip Record If...»有«Skip Record If...»--------------(1)所以,«Skip Record If...»«Skip Record If...»--------(2)又因为«Skip Record If...»存在,所以应有«Skip Record If...»---------(3)故,由(2)式及(3)式,必有«Skip Record If...».1.注意:使«Skip Record If...»的点«Skip Record If...»可能为«Skip Record If...»的极大值点(或极小值点),也可能不是.比如:«Skip Record If...»二.中值定理1.定理2.罗尔中值定理:若值设函数«Skip Record If...»满足:(1)«Skip Record If...»在区间«Skip Record If...»上连续;(2)«Skip Record If...»在区间«Skip Record If...»内可导;(3)«Skip Record If...».则,必至少存在一点«Skip Record If...»,使«Skip Record If...»注意:罗尔定理的几何意义是说,在每点处都有非垂直切线的一段曲线上,若两端点处的高度相同,则在曲线上至少存在一条水平切线.(作图说明)证明:由闭区间上连续函数的性质,«Skip Record If...»在«Skip Record If...»上有最大值M及最小值m.(1)若M=m,则«Skip Record If...»,«Skip Record If...».所以,«Skip Record If...»任取«Skip Record If...»,均满足«Skip Record If...»;(2)若«Skip Record If...»,则M和m中至少有一个不等于«Skip Record If...»,因此则M和m中至少有一个在区间内部某点«Skip Record If...»处取到.不妨设«Skip Record If...»为«Skip Record If...»的最大值,从而也是极大值。
又因 «Skip Record If...»在区间«Skip Record If...»内可导,则由费马定理知,«Skip Record If...».注意:罗尔定理中的三条件如缺少其中任何一条,则结论可能不再成立.反例1.«Skip Record If...»(不满足条件(1));反例2.«Skip Record If...»,(不满足条件(2));反例3.«Skip Record If...».2.定理3.拉格朗日中值定理:若值设函数«Skip Record If...»满足:(1)«Skip Record If...»在区间«Skip Record If...»上连续;(2)«Skip Record If...»在区间«Skip Record If...»内可导;则,必至少存在一点«Skip Record If...»,使«Skip Record If...»注意:(1)拉氏定理中,如仍有«Skip Record If...»,则结论将变为:必至少存在一点«Skip Record If...»,使«Skip Record If...».可见罗尔定理是拉氏定理的特殊情形;(3)拉氏定理的几何意义:在«Skip Record If...»上曲线«Skip Record If...»上至少存在一点«Skip Record If...»,使该点处的切线平行于弦AB.证明:令«Skip Record If...»,则«Skip Record If...»在«Skip Record If...»上满足罗尔定理的三个条件.所以,由罗尔定理知,«Skip Record If...»,使«Skip Record If...».即,«Skip Record If...»..--------(*)注意:(1)注意到(*)式当«Skip Record If...»时仍然成立;(2)为方便应用,(*)式也常改写为«Skip Record If...»-----(**)(**)式称为拉格朗日中值公式;(3)罗尔定理及拉氏定理仅指明«Skip Record If...»,具体«SkipRecord If...»的位置是什么,定理本身并未明确指出.但在大多数问题中知道这一点已经足够了。
因此我们才称上述两定理为中值定理,这个“中”其实是“内部”的意思,并非“正中间”.中值定理是利用导数的局部性态来研究函数整体性态的重要工具;(4)为了强调中值«Skip Record If...»的位置特征,可记«Skip Record If...»;(5)故拉氏定理又可写为«Skip Record If...»----(4)(6)由拉氏定理,«Skip Record If...»上式称为有限增量公式.例1.验证:«Skip Record If...»在«Skip Record If...»上满足拉氏定理的条件,并求出定理结论中的点«Skip Record If...».解:(一)1.由«Skip Record If...»,知«Skip Record If...»在«Skip Record If...»处连续,从而在«Skip Record If...»上连续;2.按左、右导数的定义不难求出«Skip Record If...»从而«Skip Record If...»在«Skip Record If...»内可导,且«Skip Record If...»因此,«Skip Record If...»在«Skip Record If...»上满足拉氏定理的条件. (二)由拉氏定理的结论:«Skip Record If...»,使«Skip Record If...».不难算得:«Skip Record If...»或«Skip Record If...»。
注意:中值定理中结论只保证中间值«Skip Record If...»的存在性,至于«Skip Record If...»是否唯一,不唯一时有几个,如何求«Skip Record If...»?定理本身并未指出.例2.设«Skip Record If...»在«Skip Record If...»上连续,在«Skip Record If...»内可导,且«Skip Record If...»证明:«Skip Record If...»使«Skip Record If...»证明:(分析寻找合适的辅助函数应用罗尔中值定理,采用倒推的方法分析.命题只须证«Skip Record If...»,使«Skip Record If...»,或者«Skip Record If...».故令«Skip Record If...»«Skip Record If...»。