三年级奥数 第三十五讲 巧求周长(一)

巧求周长奥数题三年级摘要：一、巧求周长奥数题背景介绍1.奥数题的概念和作用2.巧求周长题目的特点二、三年级巧求周长奥数题解析1.题目描述2.解题思路分析3.解题步骤详解三、巧求周长奥数题训练方法1.理解题意，分析题目类型2.掌握解题思路和方法3.多做练习，提高解题速度和准确度四、对学生的启示和建议1.培养数学兴趣和自信心2.养成良好的学习习惯和方法3.注重基础知识的学习和巩固正文：一、巧求周长奥数题背景介绍奥数，即奥林匹克数学竞赛，是一种针对中小学生的数学竞赛。

它旨在选拔和培养具有数学天赋和兴趣的学生，激发他们对数学的热爱和探索精神。

奥数题目涵盖了丰富的数学知识，包括几何、代数、组合、数论等多个领域。

巧求周长题是奥数题中的一种，主要考察学生对周长概念的理解和计算能力。

二、三年级巧求周长奥数题解析题目描述：一个正方形的周长是24 厘米，请问它的面积是多少平方厘米？解题思路分析：解决这道题的关键是让学生理解正方形周长和面积的关系。

正方形的周长等于4 个边长之和，而正方形的面积等于一个边长的平方。

因此，要求正方形的面积，只需要将周长除以4，然后求平方即可。

解题步骤详解：1.计算正方形的边长：周长24 厘米÷ 4 = 6 厘米2.计算正方形的面积：边长6 厘米× 6 厘米= 36 平方厘米所以，这个正方形的面积是36 平方厘米。

三、巧求周长奥数题训练方法1.理解题意，分析题目类型：首先要让学生理解题目的意思，明确需要解决的问题。

然后分析题目类型，找出解题的关键点。

2.掌握解题思路和方法：针对不同类型的题目，要让学生学会运用相应的解题思路和方法。

例如，对于巧求周长题，要让学生掌握正方形、长方形、圆等常见图形的周长计算方法。

3.多做练习，提高解题速度和准确度：通过大量的练习，让学生熟练掌握各种题型的解题方法，提高解题速度和准确度。

四、对学生的启示和建议1.培养数学兴趣和自信心：鼓励学生积极参与数学学习，发现数学的魅力，培养对数学的兴趣和自信心。

巧求周长
巧求周长
1、已知长方形的长和宽可以求出它的周长，那么已知长方形的周长与宽，也可以求出
长方形的长，我们可以进行逆向思维：
❖长方形的长＝(周长－宽×2)÷2。

❖长方形的长＝周长÷2－宽。

2、已知正方形的周长，求它的边长：
❖正方形的边长=周长÷4。

3、如果四边形的周长没有直接告诉，必须依据题目的条件先求出周长，再解答。

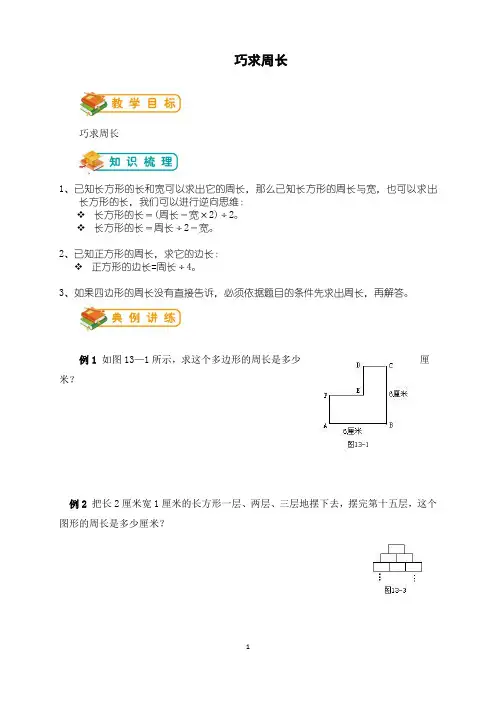
例1如图13—1所示，求这个多边形的周长是多少厘米？
例2把长2厘米宽1厘米的长方形一层、两层、三层地摆下去，摆完第十五层，这个图形的周长是多少厘米？
例3把长2厘米、宽1厘米的长方形摆成如图13—4的形状，求该图形的周长。

例4图13—6共有8条边，分别用a、b、c、d、e、f、g、h表示，要测量它的周长，至少要测量哪几条线段的长度？
例5求图13—8的周长.单位为厘米。

2.比较图13—14中哪个图形的周长长？
3.求图13—15的周长是多少厘米？
4.正方形被分成了五个长方形，每个长方形的周长都是30厘米，求这个正方形的周长是多少厘米（图13—6）？
1.一张长5分米、宽4分米的长方形纸板，从四个角上各裁去一个边长为1分米
的正方形，所剩部分的周长是多少分米？
2.如图13—10所示的多边形，它的
周长是多少厘米？
3.用15个边长2厘米的小正方形摆成如图13—11的形状，求它的周长。

4.求图13—12所示图形（每个小正方形的顶点恰在另一个正方形的中心，且边相
互平行）的周长。

5.用边长为10厘米的五个小正方形拼成如图13—13的形状，这个图形的周长是多少厘米？。

巧求周长我们知道：这两个计算公式看起来十分简单，但用途却十分广泛。

用它们可以解决许多直角多边形(所有的角都是直角的多边形)的周长问题。

这是因为直角多边形总可以分割成若干个正方形或长方形。

例如，下面的图形都可以分割成若干个正方形或长方形，当然分割的方法不是唯一的。

由此，可以演变出许多只涉及正方形、长方形周长计算公式的题目。

例1一个苗圃园(如左下图)，周边和中间有一些路供人行走(图中线段表示“路”)，几个小朋友在里面观赏时发现：从A处出发，在速度一样的情况下，只要是按“向右”、“向上”方向走，几个人分头走不同的路线，总会同时达到B处。

你知道其中的道理吗？分析与解：如右上图所示，将各个交点标上字母。

由A处到B处，按“向右”、“向上”方向走，只有下面六条路线：(1)A→C→D→E→B；(2)A→C→O→E→B；(3)A→C→O→F→B；(4)A→H→G→F→B；(5)A→H→O→E→B；(6)A→H→O→F→B。

因为A→C与H→O，G→F的路程一样长，所以可以把它们都换成A→C；同理，将O→E，F→B都换成C→D；将A→H，C→O都换成D→E；将H→G，O→F都换成E→B。

这样换过之后，就得到六条路线的长度都与第(1)条路线相同，而第(1)条路线的长“AD+DB”就是长方形的“长+宽”，也就是说，每条路线的长度都是“长+宽”。

路程、速度都相同，当然到达B处的时间就相同了。

例2计算下列图形的周长(单位：厘米)。

解：(1)将图中右上缺角处的线段分别向上、向右平行移动到虚线处(见左下图)，这样正好移补成一个正方形，所以它的周长为25×4=100(厘米)。

(2)与(1)类似，可以移补成一个长方形，周长为(10＋15)×2=50(厘米)。

例3求下面两个图形的周长(单位：厘米)。

解：(1)与例2类似，可以移补成一个长(15＋10＋15)厘米、宽(12＋20)厘米的长方形，所以周长为(15＋10＋15)×2＋(12＋20)×2＝144(厘米)。

巧求周长奥数题三年级
【最新版】
目录
1.题目概述
2.巧求周长的方法
3.例题解析
4.练习建议
正文
【1.题目概述】
巧求周长奥数题是针对三年级学生的一道经典数学题目，主要考察学生对周长概念的理解和计算能力。

在这类题目中，通常会给定一些图形，如长方形、正方形、圆形等，要求学生通过观察和分析，找到一种巧妙的方法来求解周长。

【2.巧求周长的方法】
在解决这类题目时，学生需要掌握一定的技巧，例如：长方形的周长公式是（长 + 宽）×2，正方形的周长公式是边长×4，圆形的周长公式是 2πr（其中 r 为半径）。

此外，还可以利用平移、切割等方法，将复杂的图形转化为简单的图形，从而简化计算过程。

【3.例题解析】
例题：一个长方形的长是 8 厘米，宽是 6 厘米，求这个长方形的周长。

解析：根据长方形的周长公式，周长=（长 + 宽）×2=（8+6）×2=28 厘米。

【4.练习建议】
对于这类题目，学生需要多做练习，提高自己的观察和分析能力。

可以从简单的图形入手，逐步增加难度，例如：组合图形、多边形等。

在解题过程中，要注重方法的灵活运用，善于总结和归纳，形成自己的解题技巧。

通过以上分析，我们可以看出，巧求周长奥数题虽然有一定难度，但只要掌握了基本的周长公式和解题技巧，就能够轻松应对。

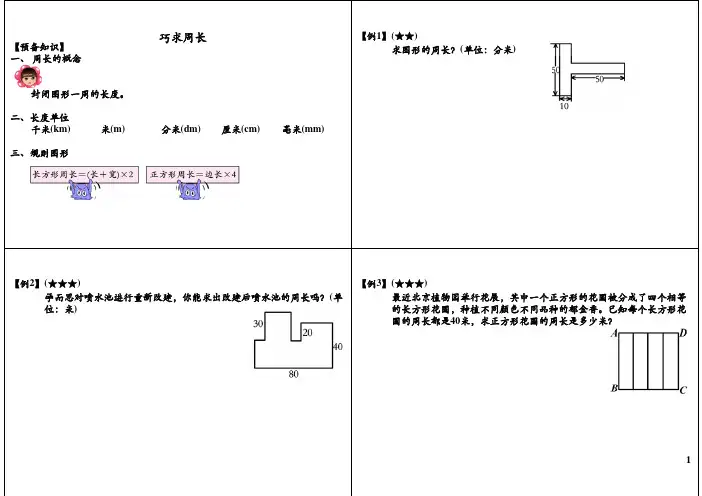
一、周长的概念
封闭图形一周的长度。

【例1】(★★)
求图形的周长？(单位：分米)
学而思对喷水池进行重新改建，你能求出改建后喷水池的周长吗？(单位：米)最近北京植物园举行花展，其中一个正方形的花圃被分成了四个相等的长方形花圃，种植不同颜色不同品种的郁金香。

已知每个长方形花圃的周长都是40米，求正方形花圃的周长是多少米？
下图是由四个一样大的长方形和一个周长是4分米的小正方形拼成的一个边长是11分米的大正方形，每一个长方形的长和宽各是多少？周长是多少？如图，长方形ABCD中有一个正方形EFGH，且AF＝16厘米，HC＝13厘米，长方形ABCD的周长为____厘米。

正方形ABCD边长为4cm，每边被四等分，你们能找出图中所有正方形并求出周长的和吗？。

巧求周长奥数题三年级
摘要：
一、问题引入
二、解题思路
三、具体步骤
四、结论与反思
正文：
一、问题引入
在我们的日常生活中，计算周长是一个常见的数学问题。

今天，我将为大家讲解一个关于巧求周长的奥数题，适合三年级的学生挑战。

希望通过这个题目，大家能够巩固周长的计算方法，提高自己的数学思维能力。

二、解题思路
要解决这道题，我们需要灵活运用周长的计算公式，并掌握一些基本的数学思维方法，如观察、分析、归纳等。

三、具体步骤
假设有一个正方形，边长为a，我们需要求解它的周长。

根据正方形的性质，我们知道正方形的四条边长相等，所以周长C=4a。

现在，假设我们有一个长方形，长为a，宽为b。

我们同样需要求解它的周长。

根据长方形的性质，我们知道长方形的对边相等，所以周长
C=2a+2b。

然而，在现实生活中，我们常常会遇到一些不规则的图形，如一个边长为
a 的正方形和一个边长为
b 的长方形组成的图形。

对于这类图形，我们可以先将它们分割成若干个规则图形，如正方形和长方形，然后分别计算这些规则图形的周长，最后将它们相加得到整个图形的周长。

四、结论与反思
通过以上分析，我们可以得出结论：巧求周长的奥数题三年级主要考察了我们对周长计算公式的掌握程度以及对数学思维方法的运用。

在解题过程中，我们需要注意观察题目的特点，分析图形的性质，归纳总结规律，并灵活运用周长公式。

巧求周长（一）
同学们都知道长方形的周长＝（长＋宽）×2，我们把长方形的周长用C表示，长用a表示，宽用b表示，长方形的周长用字母表示。

正方形的周长＝边长×4，用C表示正方形的周长，a表示
边长，正方形的周长用字母表示。

运用上面两个公式可以求出标准的长方形和正方形的周长。

今天我们要进一步学习运用长方形和正方形周长计算公式巧求周长，培养同学们灵活应用知识的能力。

（一）典型例题
例1. 下图是一块近似长方形的麦地，这块麦地的周长是多少？
例2. 下图是一个楼梯的侧剖图面，已知每步台阶宽3分米，高2分米，问这个楼梯侧面周长是多少米？
例3. 王爷爷用篱笆在一面靠墙的地方围一个长方形的菜园，这些篱笆长30米，如果这个长方形菜园长18米，宽应该是多少？
例4. 用两个长和宽分别是9分米、7分米的长方形，拼成一个大的长方形，拼成后的长方形周长最长是（）分米，最短是（）米。

例5. 街心花园有一块草坪（如下图），在草坪四周从某顶点开始每2米种一棵月季花，一共可以种多少棵月季花？
（二）试一试，独立完成
1. 一个长方形边长6分米，把它平均分成3个小长方形，求每个小长方形的周长和面积各是多少？
2. 下图是一个餐厅室的平面图，准备重新装修。

每一米长的墙壁需用50元壁纸，10元钱的胶。

请你预算一下，装修墙壁约需材料费多少元？
3. 用9个边长2厘米的小正方形摆成下图形状，它的周长是__________厘米。

4. 下图正方形被分割成4个长方形，每个长方形的周长都是20厘米，求这个正方形的周长？。