通用版本六年级数学：找规律 趣味数学(无答案)

六年级找规律奥数题
题目:找出下面每行、每列和每个九宫格中的数字,并将它们组成一个四位数。

一行:357,892
一列:461,983
一个九宫格:289,417,982,357
要求:每个数字必须被4个数字整除,且这些数字不能重复。

解法:
首先观察题目中的数字,可以发现每行、每列和每个九宫格中的数字都是唯一的。

其次,我们可以使用穷举法来寻找符合条件的数字。

从行入手,如果行中的第一个数字是357,则该数字不能被4个数字整除,因此无法继续向下寻找。

同理,从列入手,如果列中的第一个数字是892,则该数字不能被4个数字整除,因此无法继续向下寻找。

因此,我们可以将这个行、列和九宫格中所有数字都排除掉,然后再从下一个行、列和九宫格中开始寻找符合条件的数字。

最后,我们使用计算机程序来解决这个问题,可以大大加快搜索的速度。

具体地,我们可以使用一个数组来表示符合条件的数字,使用一个循环来搜索整个数组。

在搜索过程中,我们需要检查每个数字是否被4个数字整除,如果符合条件,则将其加入数组中。

时间复杂度:O(n^3)
拓展:
这个问题可以推广到更大的数字规模。

例如,如果有n行、m列和n个九宫格,我们需要找到符合条件的n位数。

我们可以使用类似的方法来解决,即使用一个数组来表示符合条件的数字,使用一个循环来搜索整个数组。

在搜索过程中,我们需要检查每个数字是否被4个数字整除,如果符合条件,则将其加入数组中。

如果数字的规模很大,那么搜索的时间复杂度将变得非常高。

因此,我们需要使用更高效的算法来解决这个问题。

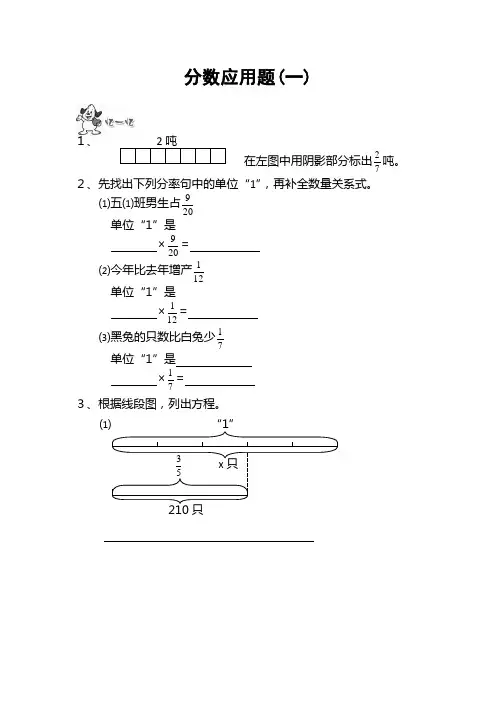
分数应用题(一)１、2吨。

在左图中用阴影部分标出7２、先找出下列分率句中的单位“1”，再补全数量关系式。

9⑴五⑴班男生占20单位“1”是9=×201⑵今年比去年增产12单位“1”是1=×121⑶黑兔的只数比白兔少7单位“1”是1=×7３、根据线段图，列出方程。

⑴“1”3x只5210只⑵ “1”x 吨 61 少5吨１、根据下列句子，画出线段图，写出数量关系式。

（你能写出几个不同的等量关系式吗？试一试） ⑴甲车从A 地到B 地，已行了72。

⑵实际节约用电1007⑶未看页数的52与已看的同样多。

２、一桶油重120千克，第一次用去它的83，第二次用去第一次的32。

⑴83120⨯表示⑵3283120⨯⨯表示⑶3283⨯表示 ３、⑴一堆煤87吨，第一次用去71，第二次又用去71吨，还剩多少吨？⑵一堆煤87吨，第一次用去71吨，第二次用去余下的71，第二次用去多少吨？⑶一堆煤87吨，第一次用去71，第二次又用去第一次的71，第二次用去多少吨？４、修一段公路，已修2000米，剩下的比已修的少41，公路全长多少米？５、小明看一本528页的童话书，他第一天读了这本书的61，第二次读了60页，第三天应从第几页读起？1，相当于长６、两个长方形重叠部分的面积相当于大长方形面积的61。

大长方形面积是120平方厘米，求小长方形小长方形面积的4面积。

1，这时剩下７、一条水渠，第一天挖了40米，第二天挖了余下的3的与挖好的正好相等，这条水渠长多少米？3后，距这条公路的中点还有17千米，８、修一条公路，修了全长的7求公路的全长。

通过本次学习，我的收获有。

第一部分必做题１、(☆)标出下列分率句中的单位“1”，画出线段图，写出等量关系式。

1。

⑴萝卜比白菜多5线段图：关系式①②3。

⑵一段钢材，用去7线段图：关系式①②4吨无烟煤。

２、(☆)学校食堂运来51，还剩多少吨？⑴第一次用去51吨，还剩多少吨？⑵第二次又用去5⑶两次共用去多少吨？1吨？⑷第三次用去多少吨后还剩5⑸第三次用去多少吨后还剩原吨数的51？３、(☆)李师傅要加工3600个机器零件，第一天加工了总数的91，第二天加工了总数的61。

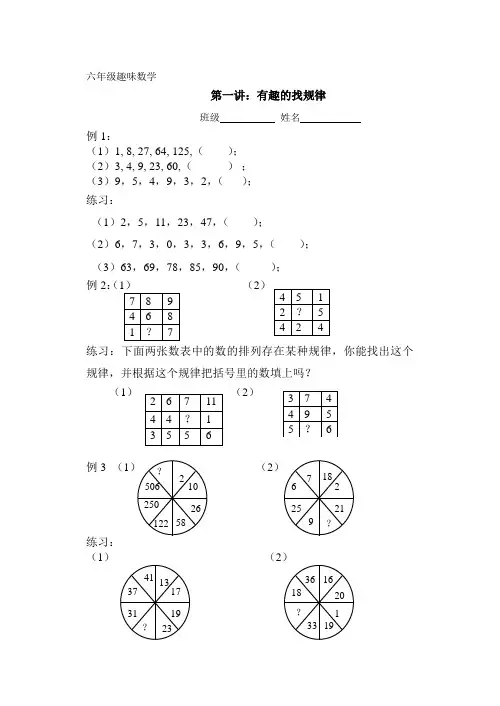
六年级趣味数学第一讲：有趣的找规律班级 姓名例1：（1）1, 8, 27, 64, 125,（ ）；（2）3, 4, 9, 23, 60,（ ） ；（3）9，5，4，9，3，2，（ ）；练习：（1）2，5，11，23，47，（ ）；（2）6，7，3，0，3，3，6，9，5，（ ）；（3）63，69，78，85，90，（ ）；例2：（（2） 练习：下面两张数表中的数的排列存在某种规律，你能找出这个规律，并根据这个规律把括号里的数填上吗？（1）（2）例3 （1（2练习：（1）（2）综合练习：1、找规律填数。

（1）2, 5, 10, 17, 28, （ ）,（ ）（2）94，46，22，10，（ ），（ ）（3）142857、428571、285714、857142、( )2、下图所示的图形中的数字都有各自的规律，先把规律找出来，再把空缺的数字填上：3. 下图所示的图形中的数字都有各自的规律，先把规律找出来，4、下图中，每个圆代表一个数码，每横行的三个圆从左到右看做一个三位数，四行表示的四个三位数是890， 784，361，256。

那么，5．下图的数之间存在着某种关系，请按照这一关系求出数a 和b 。

6 7 11 123 89 2 8 2 5 21 123 7 6 2 14 4 ？六年级趣味数学第二讲：有趣的数字谜班级姓名例1．从1～7中选出六个数字填入下式的□中，能得到的最大结果是多少？□×（□-□）÷□-□×□。

练习：1、从1～9这九个数字中选出八个填入下式的八个○内，使得算式的结果尽可能大：[○÷○×（○+○）]-[○×○+○-○]。

2、在下式的四个□内填入四个不同的一位数，要求左边的数比右边的数小，并且运算结果等于24。

□÷（□÷□÷□）=24。

例2、在下列各图中，分别从1～8中选择六个数字填入□内，使得按顺时针方向计算的各关系式成立：练习：将1～8这八个自然数填入左下图的空格中，使四边形组成的四个等式都成立。

六年级找规律练习题规律是数学中的一个重要概念，通过寻找一系列数字或对象中的规律，我们能够更好地理解数学的本质。

对于六年级的学生来说，找规律是一个相对较难的任务，需要他们运用逻辑思维和分析能力。

本文将介绍一些六年级找规律的练习题，帮助学生提高解题能力。

第一题：1, 4, 9, 16, 25, ?要找到规律，我们可以观察数字之间的差异。

首先，我们可以发现每个数字都是一个平方数，即前一个数乘以自身。

所以下一个数字是36，因为6乘以6等于36。

第二题：8, 11, 14, 17, ?这一题的规律不再是平方数，但我们仍然可以观察到每个数字之间的差异。

在这里，每个数字都增加了3。

所以下一个数字是20，因为17加上3等于20。

第三题：2, 4, 8, 16, ?这个题目相对复杂一些，但我们仍然可以通过观察数字之间的差异来找到规律。

注意到，每个数字都是前一个数字乘以2。

所以下一个数字是32，因为16乘以2等于32。

第四题：1, 10, 100, 1000, ?这个题目看似更加困难，但仍然可以通过观察数字之间的差异来找到规律。

注意到，每个数字都是前一个数字乘以10。

所以下一个数字是10000，因为1000乘以10等于10000。

通过以上练习题，我们可以看到找规律的方法有很多种。

有时可以通过观察数列中的差异，有时可以通过乘法或除法运算等方式来找到规律。

当然，这些只是一些简单的例子，实际上数学中的规律更为复杂多样。

对于六年级的学生来说，培养找规律的能力非常重要，因为这将对他们以后的数学学习产生积极影响。

通过不断练习和思考，他们可以逐渐提高解题能力，更好地理解数学的本质。

总结：六年级找规律练习题是培养学生逻辑思维和分析能力的重要工具。

通过观察数字之间的差异和运算规律，学生可以逐渐提高解题的准确性。

通过不断的练习和思考，他们会变得越来越擅长找规律，从而更好地应对数学学习中的各种挑战。

加油，六年级的小朋友们！。

六年级找规律练习题在数学学科中，找规律是一个非常重要的能力。

六年级是一个适合培养孩子们找规律的年级。

通过练习找规律题，孩子们可以锻炼自己的逻辑思维能力，培养观察和分析问题的能力。

下面是一些六年级找规律练习题，帮助孩子们提高他们的数学能力。

练习题1：数列找规律观察下面的数列，找出规律并补充下一个数字。

1, 3, 5, 7, __找规律：每个数字都增加了2。

补充数字：9练习题2：图形找规律观察下面的图形，找出规律并绘制下一个图形。

▢▣◯找规律：每个图形都在原有基础上增加一个角。

绘制图形：◊练习题3：运算找规律观察下面的运算式，找出规律并计算下一个运算式的结果。

2 + 2 = 43 + 3 = 64 + 4 = 85 + 5 = __找规律：每个运算式中的两个数字相加等于结果。

计算结果：10练习题4：图形排列找规律观察下面的图形排列，找出规律并补充图形。

△△△▲ ▲ ▲△△ __找规律：每一列的图形交替排列。

补充图形：▲练习题5：递增数列找规律观察下面的递增数列，找出规律并补充下一个数字。

2, 4, 8, 16, __找规律：每个数字都是前一个数字乘以2。

补充数字：32练习题6：几何图形找规律观察下面的几何图形，找出规律并绘制下一个图形。

■ ■ ■□ □ □ □■ ■ __找规律：图形排列方式为一个大正方形，里面有一个小正方形。

绘制图形：□ □ □ □■通过以上的找规律练习题，孩子们可以锻炼他们的观察力和逻辑思维能力。

找规律是数学学科中一个非常重要的能力，它不仅帮助我们解决数学问题，还能培养我们的思考和分析问题的能力。

在六年级阶段，提前培养孩子们找规律的能力可以为他们在后续学习数学的过程中打下坚实的基础。

因此，希望孩子们能够积极参与这些找规律练习题，不断提高自己的数学水平。

六年级知识点找规律题在六年级的学习中，我们经常会遇到一些需要找规律的数学题目。

这些题目要求我们观察一系列数字或形状的变化，然后找出其中的规律，以便解决问题。

掌握找规律的方法对于解决数学问题非常重要。

本文将介绍一些常见的找规律题目和解题技巧。

一、数字规律题数字规律题是六年级最常见的找规律类型题目。

下面我们以几个例子来说明：例1：找出下列数列中的规律，并将规律应用到下一个数字上。

1, 4, 9, 16, 25, ?观察这个数列，我们可以发现每个数字都是前一个数字的平方。

根据这个规律，下一个数字应该是36。

例2：找出下列数列中的规律，并将规律应用到下一个数字上。

2, 4, 8, 16, 32, ?观察这个数列，我们可以发现每个数字都是前一个数字乘以2得到的。

根据这个规律，下一个数字应该是64。

通过以上例子，我们可以看出，在数字规律题中，经常需要观察数字之间的关系，如加减乘除、平方、立方等。

只要我们找到了这种关系，就能够应用到下一个数字上，找出正确的答案。

二、形状规律题除了数字规律题，六年级中也会遇到一些形状规律题。

下面我们以几个例子来说明：例1：找出下列形状中的规律，并将规律应用到下一个形状上。

□, ■, △, ○, ?观察这个形状序列，我们可以看出形状在不断交替出现，且每个形状都是前一个形状的三角形补集。

根据这个规律，下一个形状应该是□。

例2：找出下列形状中的规律，并将规律应用到下一个形状上。

△, ■, ○, △, ?观察这个形状序列，我们可以看出形状在不断交替出现，且每个形状都是前一个形状顺时针旋转90度得到的。

根据这个规律，下一个形状应该是■。

在形状规律题中，我们需要关注形状的属性，如形状类型、数量、位置、旋转等。

只要我们找到了这些属性的变化规律，就能够应用到下一个形状上，找出正确的答案。

三、解题技巧在解决找规律题的过程中，有一些常用的技巧可以帮助我们更快地找到规律：1. 观察并列举：在观察数列或形状序列时，可以将每个数字或形状写下来，然后逐个比较它们之间的关系，列举出所有可能的规律。

解救懒羊羊
懒羊羊被灰太狼抓走啦！！！
救救我嘿嘿，这次你再也跑不掉了，我可是布
置了天罗地网
嘿嘿，我在狼堡外面布置了六重关卡，喜羊羊你们休想接近狼堡！
喜羊羊他们赶到狼堡时，发现情况不妙，但是这难不倒他们！
这么多复杂的关卡，灰太狼自己也要回家，这里一定有过关的
线索！
村长来帮忙：
村长发明了透视眼镜，带上它就会找到被灰太狼掩藏起来的记号！
果然，喜羊羊他们很快找到第一个记号。

记号2：
记号3：
记号4：
记号5：
记号6：
喜羊羊终于及时的救出了懒羊羊，灰太狼又失败啦！
小朋友们，因为喜羊羊平时爱动脑，爱思考，他
才会这么快带着大家救出了同伴。

这就是学习的力量哦！！！。

六年级数学找规律题导言找规律是数学中一种重要的思维方法，也是培养学生逻辑思维和创新思维的有效方式。

在六年级数学中，找规律题占据了相当的比例，并且往往是考试中的考点。

本文将介绍六年级数学中常见的找规律题，并给出解题思路和解题步骤。

一、顺序找规律题顺序找规律题是最简单的一类找规律题，题目中给出一组数按照某种规律顺序排列，要求学生找出这种规律，并继续按照规律找出下一个数。

例如：例题1： 8，12，16，20，24，__。

解题思路：观察这组数，我们可以发现，每个数都比前一个数大4。

因此，下一个数是24+4=28。

所以，答案是28。

例题2： 1，4，9，16，25，__。

解题思路：观察这组数，我们可以发现，每个数都是前一个数的平方。

因此，下一个数是25的平方，即25x25=625。

所以，答案是625。

二、运算找规律题运算找规律题是指题目中给出一组数进行某种运算后得到另一组数，要求学生找出这种运算规律，并运用规律求出下一个数。

例如：例题3： 2，4，6，8，10，__。

解题思路：观察这组数，我们可以发现，每个数都是前一个数加上2。

因此，下一个数是10+2=12。

所以，答案是12。

例题4： 3，6，12，24，48，__。

解题思路：观察这组数，我们可以发现，每个数都是前一个数乘以2。

因此，下一个数是48x2=96。

所以，答案是96。

三、图形找规律题图形找规律是数学中较为复杂的一类找规律题，题目中给出一组图形按照某种规律排列，要求学生找出这种规律，并继续按照规律排列图形。

例如：例题5：□□ ■□ ■ □□ ■ □ ■解题思路：观察这组图形，我们可以发现，每一行都是交替出现□和■，并且每一行的个数与行数相等。

因此，下一个图形是：□□ ■□ ■ □□ ■ □ ■□ ■ □ ■ □例题6：■■ ■■ □ ■■ ■ ■ ■解题思路：观察这组图形，我们可以发现，每一行首尾都是■，中间是空位□。

因此，下一个图形是：■■ ■■ □ ■■ ■ ■ ■■ □ □ □ ■四、其他类型找规律题除了以上三种常见的找规律题型外，还有一些其他类型的找规律题。

六年级找规律数学题一、数字规律1. 按规律填数：1，3，6，10，15，（），28。

- 解析：观察这组数字，1到3增加了2，3到6增加了3，6到10增加了4，10到15增加了5。

可以发现相邻两个数的差值在依次递增1。

那么15后面的数应该比15大6，即15 + 6 = 21。

验证一下，21到28增加了7，符合规律。

所以括号里应填21。

2. 数列：2，4，8，16，32，（）。

- 解析：这组数列中，2×2 = 4，4×2 = 8，8×2 = 16，16×2 = 32。

可以得出规律是后一个数是前一个数的2倍。

所以括号里的数应该是32×2 = 64。

二、图形规律1. 用小棒按照如下方式摆三角形：摆1个三角形需要3根小棒；摆2个三角形需要5根小棒；摆3个三角形需要7根小棒……（1）摆10个三角形需要多少根小棒？- 解析：观察可得，摆1个三角形用3根小棒（3 = 2×1+1）；摆2个三角形用5根小棒（5 = 2×2 + 1）；摆3个三角形用7根小棒（7 = 2×3+1）。

可以总结出规律，摆n个三角形需要2n + 1根小棒。

当n = 10时，2×10+1 = 21根小棒。

（2）有21根小棒，可以摆多少个三角形？- 解析：根据前面总结的规律2n+1。

设可以摆n个三角形，则2n + 1 = 21，2n = 20，解得n = 10。

所以21根小棒可以摆10个三角形。

2. 下列图形是由同样大小的小圆圈按照一定规律所组成的，其中第1个图形中一共有6个小圆圈，第2个图形中一共有9个小圆圈，第3个图形中一共有12个小圆圈……（1）第5个图形中有多少个小圆圈？- 解析：观察图形，第1个图形有6 = 3×1+3个小圆圈；第2个图形有9 = 3×2 + 3个小圆圈；第3个图形有12 = 3×3+3个小圆圈。

可以得出规律，第n个图形有3n+3个小圆圈。

六年级找规律奥数题找规律是奥数中常见的题型之一，要求学生通过观察数列或图形中的特点，找到其中的规律，并根据规律解答问题。

下面是几道六年级找规律的奥数题及其解题思路的相关参考内容：1. 题目： 2, 4, 8, 16, 32, ?解题思路：观察这个数列，可以发现每个数字都是前一个数字的2倍。

因此，下一个数字应该是32的2倍，即64。

答案：642. 题目： 3, 7, 15, 31, ?解题思路：观察这个数列，可以发现每个数字都是前一个数字的2倍再加1。

因此，下一个数字应该是31的2倍再加1，即63。

答案：633. 题目： 1, 2, 4, 7, 11, ?解题思路：观察这个数列，可以发现从第二个数字开始，每个数字都是前一个数字加上一个递增的数字。

第一个递增数字是1，第二个递增数字是2，第三个递增数字是3，以此类推。

因此，下一个数字应该是11加上递增数字4，即15。

答案：154. 题目： 1, 4, 9, 16, 25, ?解题思路：观察这个数列，可以发现每个数字都是前一个数字的平方。

因此，下一个数字应该是25的平方，即625。

答案：6255. 题目： 2, 5, 10, 17, ?解题思路：观察这个数列，可以发现每个数字都比前一个数字大2，4，6，8...。

因此，下一个数字应该比17大10，即27。

答案：276. 题目： 1, 4, 9, 16, 25, ?解题思路：观察这个数列，可以发现每个数字都是前一个数字的平方。

因此，下一个数字应该是25的平方，即625。

答案：6257. 题目： 1, 3, 6, 10, ?解题思路：观察这个数列，可以发现每个数字都是前一个数字加上一个递增的数字。

第一个递增数字是2，第二个递增数字是3，第三个递增数字是4...因此，下一个数字应该是10加上递增数字5，即15。

答案：15通过以上的例题可以看出，在解答找规律的问题时，可以通过观察数列或图形中数字的变化，找到其中的规律。

趣味数学——找规律
找规律是常见的数学题型。

目的是让学生发现图形和数字的排列规律，从而理解并掌握找规律的方法，培养学生的观察及推理能力。

例如数列1，2，4，7，11，16，〔〕，〔Y〕。

其中和Y的值分别为多少呢？数列中两
数之间的差成一个等差数列关系，相差为：1，2，3，4，5，6。

因此值为22，Y的值为29。

今天我们用Python解决一道奥数找规律问题：现有一组数列为1，2，5，13，34，〔z〕。

请问z的值为多少呢？
这个数列的规律你发现了吗？第N个数字等于它前一个数字加前面所
有数字的和，例如5=2+2+1，13=5+5+2+1，34=13+13+5+2+1。

那么如何用Python表示出这个数列呢？并求出需要的答案呢？
首先设变量a=1表示第一个数字。

设置两个循环变量i和num用来统
计元素是否到达规定的个数，这种变量也称为计数器，并且定义列表arr
用于存放输出的结果。

控制while循环设置计数器和产生元素的个数，在每次循环结束前加1，在循环过程中，数值不断累加，计数器也加1，第i次循环加上一次
的結果，计算出结果后将计算出的新元素添加到arr列表中，并且把元素
i清零，这样下次循环又是从第一个数字开始累加，依次循环，直到全部
结束为止，每循环一次，打印显示列表值，用于观察〔图1〕。

通过分析，我们可以用Python计算出有规律的数列，并且有序将每
次的列表中的值输出，那么现在增加难度：如果我们想求出该数列中第
100个数的值是多少？前100个数值之和为多少呢？大家赶紧动手编写代
码吧。