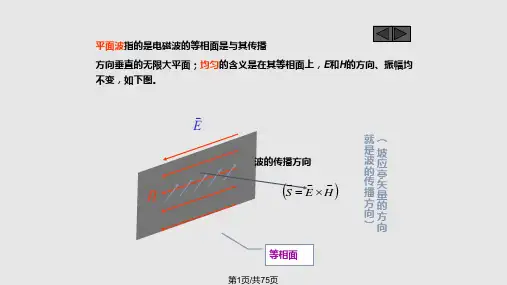
理想介质中均匀平面波演示

E y
k2
E y
,
d2 d
H z x2
k 2H z
式中 k j j —传播常数 ( propagation constant)，
通解 E y E e j x E e j x
H z
H e j x H e j x
1 (E ej x E e j x ) Z0
2 —波数、相位常数 ( phase constant) rad/m ，
特点：Ey 和 Ez 振幅相同，相位差90°。
合成后 E Ey2 Ez2 C 即 Ey2 Ez2 C2
tanα Ez tan( t )
Ey
Ey 超前 Ez 为右旋极化波。 Ey 滞后 Ez 为左旋极化波。
图6.4.2 圆极化的平面波
返回 上页 下页
椭圆极化（Elliptical Polarization)
返回 上页 下页
感 谢 观 看
H z H ze xe j x H ze xe j x
振幅呈指数衰减,电磁波是减幅波。
当 ，称为良导体， ' ，忽略位移电流。 j
k2 j , k j (1 j) 1 (1 j)
2
d
1 2d
返回 上页 下页
良导体中波的传播特性： E , H 为减幅波（集肤效应) ； 波阻抗为复数, E 超前 H 45
图6.2.1 理想介质中正弦均匀 平面波沿 x 方向的传播
返回 上页 下页
例 6.2.1 自由空间中 B 106 cos(6π 108t 2πz)(ex ey ) 试求：a. f ,v,, 及传播方向；b. E 和 S。
解：a. 波沿 z 轴方向传播; 2π rad/m
2π 1 m f 2π 3108 Hz

2014-6-13
9
例1 已知无界理想媒质(ε=9ε0, μ=μ0，σ=0)中正弦均匀平面电磁
波的频率f=108 Hz， 电场强度
jkz j
E ex 4e
试求：
jkz

3
ey 3e
V / m
(1) 电磁波的相速度vp、波长λ、相移常数k和波阻抗η； (2) 电场强度和磁场强度的瞬时值表达式； (3) 与电磁波传播方向垂直的单位面积上通过的平均功率。 10
若电场强度E和磁场强度H只是直角坐标z和时间t的函数：
E E H H 0, 0, 0, 0 x y x y
2014-6-13
1
设电场只有x方向分量，磁场只有y方向的分量，则电场、磁 场及传播方向满足下图：
思考：有电磁场的区域，是否一定有电磁波存在？
2014-6-13
2
j (t kz )
] ex E0 m cos(t kz 0 )

e j (t kz ) ]

cos(t kz 0 )
5
e y H 0 m cos(t kz 0 )
2014-6-13
2014-6-13
理想介质中均匀平面电磁波的电场和磁场空间分布
.


2014-6-13
12
5 2 W /m 坡印延矢量的时间平均值： Sav Re[ S ] ez 16
与电磁波传播方向垂直的单位面积上通过的平均功率：
（3）复坡印廷矢量： 1 S EH* 2 j kz j kz 1 3 1 jkz jkz 3 3 ex 4e e y 3e e ey e ex 2 40 10 5 ez W / m2 16

2
6.1.1 波动方程的解
在无源的理想介质中，由第5章我们知道，时谐电磁场 满足复数形式的波动方程 2Ek2E0
其中 k
对于均匀平面波，假设场量仅与坐标变量z有关，与x、
y无关，即
E E 0 x y
方程化简为
d2E k2E 0 d z2
解得
EE0ejk zE0 'ejk z
3
其中
E
0
其定义为
z 20lg Exm
Ex
z ln E xm
Ex
（dB） （Np）
波的振幅不断衰减的物理原因是由于电导率引起的焦
耳热损耗，有一部分电磁能量转换成了热能 。
26
（2）导电媒质中的相速为 vp
称为相位常数（phase constant），即单位长度上的
相移量。与理想介质中的波数k具有相同的意义。
得 ( j) 2 2 2 2 j 2 ( 1 j )
上式两边虚、实部分别相等，可得
2 1( )2 1
2
2
1( )2＋ 1
2
24
为讨论方便起见，假设电场只有x方向分量，因
而电磁波的解为
E x E xe m j x e z E xe m z e j z j x
H yE xe m jxe zE xe m zejz jx
00
vp / f 是电磁波的波长 ，k称为波数（wave-number）
或相位常数(phase constant)，表示单位长度内的相位变化。
2f 2
k
vp vp
14
x
E
O
z
y H
图6-1 理想介质中均匀平面波的传播
15
（4）均匀平面波传输的平均功率流密度 矢量可由式（6-7）和（6-8）得到

E exEx ey Ey
两个分量可以表示成为
Ex

E e jkz jx xm
Ey

E e jkz jy ym
第六章 平面波
合成场矢量E可以写为
E ex Exme jkz jx ey Eyme jkz jy
瞬时值表达式分别为
Ex Exm cos(t kz x ) Ey Eym cos(t kz y ) E ex Exm cos(t kz x ) ey Eym cos(t kz y )
E2

1 4

E02e2az
第六章 平面波
平均磁能密度：
wav,m

1 4
H
2

1 4
E02
2
f
e2az

1 4

E02
e2
az
1 ( )2
总的平均能量密度：
wav

wav,e

wav,m

1 4

E02e2
z

1 4

E02e2
z
1 ( )2

1 4

E E
Ex2

E
2 y

Em
合成场矢量E与x轴正方向的夹角α为

arctan
Ey Ex

arctan

sin(t cos(t
x x
) )


(t

x
)
圆极化波有左旋和右旋之分，规定如下：
将大拇指指向电磁波的传播方向，其余四指指向电
第六章 平面波
场矢量E矢端的旋转方向，若符合右手螺旋关系，则 称之为右旋圆极化波；

上式中 t 称为时间相位。
kz 称为空间相位。空间相位相 等的点组成的曲面称为波面。
由上式可见，z = 常数的波面 为平面，因此，这种电磁波称为 平面波。 因 Ex(z) 与 x, y 无关，在 z=常数 的波面上，各点场强相等。因
此，这种波面上场强均匀分布的平面波又称为均匀平面波。
整理版课件
10
r r
9
v p 1m f
k 2 rad / m vp
u r 120 1 40
0 整理r 版课件
9
26
(2)
H j E 1(eyejk e zx3 ejk jz 4) (A /m )
E (t)RE ej [t]
e x4co 2 s1(8t0 2 z)e y3c o 2 s 18t0 2 z 3 (V/m )
S av 1 2R [E e H * ]2 1R [E e (e z E *) ]e zE 2 m 2
可见，电磁波能量沿波的传播方向流动。
整理版课件
16
归纳理想介质中的均匀平面波的传播特点：
✓电场、磁场、与传播方向之间互相垂直，是横电磁波 (TEM波)；
✓电场与磁场的振幅不变； ✓波阻抗为实数，电场与磁场同相位； ✓电磁波的相速与频率无关； ✓电场的能量密度等于磁场的能量密度。
40
ey
1 ej
10
kz
ez
5 W/m2
16
坡印延矢量的S 时a间v 平R 均值S ~ e：] [e z156W /m 2
与电磁波传播方向垂直的单位面积上通过的平均功率：
5
PavSSav整d理S版课件16W
28
5.2 平面波的极化
5.2.1 极化的概念
➢前面讨论平面波的传播特性时，认为平面波的场强方向与时 间无关。一般情况下，沿z轴传播的均匀平面波的电场强度 不仅具有 x 分量，还具有 y 分量，根据矢量相加原理，可以 得到总电场；

Exm Eym Em
x y
2
则
Ex Em cos(t x )
E y Em cos(t x ) Em sin(t x ) 2
第六章 平面波
合成场矢量E的大小为
2 E E Ex2 E y Em
合成场矢量E与x轴正方向的夹角α为
合成场矢量E的大小为
2 2 2 2 E E Ex Ey Exm E ym cos(t )
合成场矢量E与x轴正方向的夹角α为
arctan
Ey Ex arctan Eym Exm 常数
第六章 平面波
同理，假设 Ex 和 Ey 两个分量反相，即 φx-φy=π ，则合 成场矢量E的大小为


2 1 ( ) 1 2
导电介质的波阻抗
f 1/ 2 (1 j ) f e j f j
第六章 平面波
相速
vp dz 1 [ dt 1 ]1/ 2 1 ( )2 1 2
第六章 平面波
平面电磁波 : 等相面为平面的电磁波，并且它的等相 面是与电磁波的传播方向相垂直的无限大平面。平面 电磁波简称为平面波，它是矢量波动方程的一个特解。 均匀平面波 : 对于平面波而言，如果其等相面无限大， 而且等相面上各点的场强大小相等、方向相同，即沿 着某个传播方向的平面波的场量除了与时间有关之外， 只与电磁波传播方向的坐标有关，而与其它方向的坐 标无关，即平面波的电场和磁场只沿着波的传播方向 变化，而在等相面内电场和磁场的方向、振幅以及相
arctan
Ey sin(t x ) arctan (t x ) Ex cos(t x )

理想介质中均匀平面波的 场矢量分布图
第六章 平面波
均匀平面波的传播参数： 波长

2 k
波数
k 2

波矢量
k ex kx ey k y ez kz nk
第六章 平面波
周期与频率
f 1 T 2
相速
vp dz 1 dt k
复坡印廷矢量
第六章 平面波
平面电磁波 : 等相面为平面的电磁波，并且它的等相 面是与电磁波的传播方向相垂直的无限大平面。平面 电磁波简称为平面波，它是矢量波动方程的一个特解。 均匀平面波 : 对于平面波而言，如果其等相面无限大， 而且等相面上各点的场强大小相等、方向相同，即沿 着某个传播方向的平面波的场量除了与时间有关之外， 只与电磁波传播方向的坐标有关，而与其它方向的坐 标无关，即平面波的电场和磁场只沿着波的传播方向 变化，而在等相面内电场和磁场的方向、振幅以及相
* E0 1 1 * jkz S E H e x E0e e y e jkz 2 2
E02m ez 2
均匀平面波的波数、相速与 波长之间的关系示意图
第六章 平面波
电磁波的能量密度
电磁能量的时间平均值：
1 wav,e E02m 4 1 wav,m H 02m we 4 1 wav wav,e wav,m E02m 2
第六章 平面波
等效复介电常数
f j (1 j )
复等效波数以及传播常数
复等效波数：
传播常数：
j
k 2 2 f
第六章 平面波
衰减常数α ：描述平面波每单位距离的衰减程度 传播常数β ：每单位距离滞后的相位 且

µ0 = 120π ≈ 377 Ω 在自由空间中 η 0 = ε0
2012-3-19
9
理想介质中均匀平面波的特性： 理想介质中均匀平面波的特性：
以 z 轴方向传播的波为例 1、均匀平面波为横电磁波－－ 、均匀平面波为横电磁波－－TEM波。 －－ 波 (电场与磁场均垂直于传播方向的平面波） 电场与磁场均垂直于传播方向的平面波） 电场与磁场均垂直于传播方向的平面波 2、 Ex 与 Hy 、 Ey与 Hx 可单独存在。 、 可单独存在。 且
k = ω µε ，υ = 由于 µε
所以
2012-3-19
1
ν
νT
λ
υ =λf
8
磁场可以由
r r ∇ × E = − jωµ H 求出
r r Em 经推导得： 经推导得： H ( z , t ) = e y cos (ωt − kz )
η
其中
µ η= = k ε
ωµ
,η叫作波阻抗或本征波阻抗，单位为Ω
2012-3-19
15
解（1 ） v p =
λ=
k=
η=
1
µε
vp f
2π
=
c
εr
=
3 × 10 8 9
= 108
m/s
=1 m= 2π rad/mΩ Nhomakorabeaλ
µ 1 1 = η0 = 120π = 40π ε 9 εr
2012-3-19
16
（2 ）
π r r 1 − jkz + j r 1 − jkz + j π 3 3 H = e y Em e = ey e η 10π
Ex = Em cos k ( z − υ t ) = Em cos (ωt − kz ) 其中ω = kυ =

2
选用直角坐标系，假设均匀平面波沿z方向传播，则
电场强度 E 和磁场强度 H 都不是x和y的函数 E E H H 0 0 x y x y
又： E 0, H 0 Ez H z 0, 0,由Ez，H z的波动方程可得： x y Ez =0，H z 0

17
1 4 4 8 ez ex 10 cos(2 10 t z ) 60 3 6 ey 4 4 8 10 cos(2 10 t z ) 60 3 6 (3) S (t ) E (t ) H (t ) ez 4 8 2 8 10 cos (2 10 t z ) 60 3 6 108 1 T S av S (t )dt ez W / m2 T 0 120 4 4 j z j ey 4 j 3 z j 6 H 104 e 3 6 另解： ex10 e E 60 8 1 10 S av Re[ E H ] ez W / m2 2 120 18
jkr j E E0e (复数形式） E E0 cos(t k r ) (实数形式） 式中：E0 ＝E0 表示电磁波中电场的幅度
8
表示电磁波动的角频率
k 为波矢量 为波的初始相位
E0 的方向表示电磁波中电场的方向
5、场量 E ， 的关系 H jkr jkr E E0e ) j H (E0e B E j B jkr t j H jk (E0e ) k 为表示波传播方向 H k E 的单位矢量。
3
这表明沿z方向传播的均匀平面波的电场强度和磁场 强度都没有沿传播方向的分量，即与传播方向垂直，这

S av ( ： z)

S ( z ) R e ( E H ) a v
设
j j k z e E a Ee a E e e xx 0

j k z 0 x x
j k z j j k z e H a He a H ee 0 y y y y 0
2
令
k
2 2 2
dE z ) 2 x( E z )0 x( 2 dz
2

其中:
为传播常数;
为相位常数.
在此其与波数k相同
j
rad m
实数
方程的解：

() z e E E
x x 0



z
e E


z x 0
E x E x0 e E x0 e
8 x
2 2 rad /m
1
2
即
j (t z) E(z, t) Im[ ax 20 2e ] jz jt Im[ ax 20 2e e ] Im[ ax 20 e
复振幅 jz jt
2

e
]
复有效 j 2 z x 值 E ( z ) a 20 e (V/m) x x 由于电场（x)、磁场、传播方向(z)符 合右手螺旋定则：故磁场为 y 方向。
E 1 1 1 2 w( zt , ) H zt ,) E y ( x 2 2 2
则 故
w ( z , t ) w ( z , t ) e m
对均匀平面波来说, 电场能量密度与磁场能量密 度相等。

y
x
时；即Ey分量的相位比Ex落后/2时；转动角速度
2
y
dα 0
dt
即矢量E以角速度逆时针方向转动，转 动方向和波的传播方向(+z方向)构成右 手螺旋。
---右旋园极化
Ex
x
Ey
E
(b) 右旋圆极化
第26页/共75页
3. 椭圆极化波 一般地： 若Ex和Ey分量的振幅和相位均不相等，则构成椭圆极化。
eˆx 4e
jkz
eˆy 3e
jkz
j
3
V /m
试求：(1) 均匀平面电磁波的相速度vp、波长λ、相位常数k和波阻抗η； (2) 电场强度和磁场强度的瞬时值表达式；
(3) 与电磁波传播方向垂直的单位面积上通过的平均功率。
第14页/共75页
解： (1)
vp
1
vp 1m
f
c 3108 108m / s
合成波电场E矢量的转动角速度：
dα
dt
讨论：
当
y
x
时；即Ey分量的相位比Ex超前/2时；转动角速度
2
y
dα 0
dt
即矢量E以角速度顺时针方向转动，转 动方向和波的传播方向(+z方向)构成左 手螺旋。
---左旋园极化
Ex
x
Ey
E
第25页/共75页
(a) 左旋圆极化
讨论：
dα
dt
当
3
40
e j
kz 3
eˆy
1
10
e
jkz
eˆz
5
16
W
/
m2
Pav
S
Sav

在理想介质中，散射系数通常是一个恒定的值，表 示波在单位路径上受到的散射程度。
吸收系数
吸收系数描述了波在传播过程中能量被介质吸收 的程度。
吸收系数与介质的电导率、磁导率和介电常数等 因素有关。
在理想介质中，吸收系数通常是一个恒定的值， 表示波在单位路径上被吸收的能量。
散射与吸收的物理机制
散射机制
当波遇到介质中的微小粒子时，粒子会将部分波的能量反射回周围空间，形成 散射现象。散射的程度取决于粒子的尺寸、形状和分布情况。
吸收机制
当波在介质中传播时，介质中的分子或原子会与波相互作用，将部分波的能量 转化为热能或其他形式的能量，导致波的能量逐渐减少。吸收的程度取决于介 质的电导率、磁导率和介电常数等因素。
根据不同介质界面，菲涅尔公式有不同的形式， 但都反映了能量守恒和边界条件。
应用范围
适用于理想介质和非理想介质，是研究波传播的重要工具。
04
均匀平面波的散射与吸收
散射系数
01
散射系数描述了波在传播过程中受到介质中微小粒 子散射的程度。
02
散射系数与介质的微观结构、波长以及入射角度等 因素有关。
03
高频电磁波在真空中的传播
高频电磁波
01
高频电磁波是指频率较高的电磁波，如可见光、紫外线和X射线
等。
真空中的传播
02
在真空中，由于没有介质吸收和散射，高频电磁波可以以光速
传播。
电磁场
03
高频电磁波是由变化的电场和磁场相互激发而传播的。
低频声波在液体中的传播
低频声波
低频声波是指频率较低的声波，如次声波。
能量与功率流密度
能量密度
在理想介质中，均匀平面波的能量密度是指单位 时间内通过单位面积的能量。

理想介质中的平面波若介质中的传导电流与位移电流相比完全可以忽略，这样的介质称为理想介质，或称为完全介质、无损耗介质(σ = 0)。

由前面，我们有：220ωμε∇+=E E令22k ωμε=对于给定频率，它是一个常数。

由此得：220k ∇+=E E此方程称为其次亥姆霍兹矢量方程。

由此我们得到三个其次亥姆霍兹标量方程：220x x E k E ∇+= 220y y E k E ∇+=220z z E k E ∇+=现在，我们用分离变量法先求解第一个方程。

令(,,)()()()x x E E x y z X x Y y Z z ==将其带入第一个方程，并除以XYZ ，我们得到：22222221d 1d 1d 0d d d X Y Zk X Y Z x y z+++= 重新整理为：22222221d 1d 1d d d d X Y Z k X Y Z x y z ++=- 上式左边仅是x 和y 的函数，而右边仅是z 的函数，它们相等只能说明它们等于同样一个常数。

我们将此常数写为2z k 。

因此，我们得到：222d 0d z Zk Z z+= 重复此过程，我们还可得到：222d 0d x Xk X x+= 222d 0d y Y k Y y+= 2x k 和2yk 也是常数。

三个分离变量常数k x 、k y 和 k z 并不全是独立的，它们满足： 2222x y z k k k k ++=由于我们仅对行波解感兴趣，对于前行波，场的相位随坐标变量的增加而延迟。

因此，我们得到上面方程前行波解为：x y z ik x f ik yf ik zf X X e Y Y eZ Z e ===下标表示前行（forward-traveling ）即有：i x xf E E e =k x式中E xf = X f Y f Z f 。

同样地有：i y yf E E e =k x i z zf E E e =k x式中E xf 、E yf 和E zf 为积分常数。

P. 17 / 41 .
5) 波阻抗 Zw：横向电场与横向磁场乊比
H j E
H y H y 0e jkz
Ex k Hy
H z H y ex e x j E x y z =0 H y dH y jkH y 0e jkz jkH z dz
P. 10 / 41 .
在线性各向同性均匀媒质中，k
为实数，则通解：
ቤተ መጻሕፍቲ ባይዱ
E x E x 0e jkz E 0e jkz x
E y E y 0e jkz E 0e jkz y
同理
H x H x 0e jkz H 0e jkz x
v
Ei Ei H i H i 0 x y x y (i x , y, z )
y
o
z
§6.1 均匀平面波在理想介质中的传播 作者：杨茂田
P. 3 / 41 .
对无源区（充满线性各向同性均匀理想介质）： H j E , E j H
jkz 令E y 0
E y 0e
je y
( z ) E e j (ey kz ) Ey y0
E x ( z ) e j t E x 0 cos( t kz ex ) E x ( z , t ) Re
1) 若均匀平面电磁波在∞线性各向同性均匀媒质沿－z方向 传播，则场强复矢量如何表示？ 2) 若改为沿 +x 或 +y 方向传播，则场强复矢量又如何表示？
1 H y H x Ez 0 x j y j E y E x Hz 0 x y

第5章
均匀平面波在无界空间 中的传播
5.1 5.2
理想介质中的平面波 电磁波的极化
5.3
5.4
均匀平面波在导电媒质中传播
色散和群速
5.5
均匀平面波在各向异性媒质中的传播
5.1 理想介质中的均匀平面波
均匀平面波：电磁波的场矢量只沿着它的传播方向变化， 在与波传播方向垂直的无限大平面内，电场强度和磁场强度的 方向、振幅和相位都保持不变。
E ex Ex ( z) ey E y ( z) H ex H x ( z) ey H y ( z) 假设E ex Ex (z) Ex E1e jkz E2e jkz
Ex ( z, t ) E1m cos(t kz 1 ) E2m cos(t kz 2 )

f

T
理想介质中的均匀平面波的传播特点
电场、磁场与传播方向之间相互垂直，是横电磁波（TEM 波）。均匀平面波是TEM波，反之不成立。
x
无衰减，电场与磁场的振幅不变。
O
E
波阻抗为实数，电场与磁场同相位。
y
H
电磁波的相速与频率无关，无色散。
理想介质中均匀平面波的 E 和 H
z
电场能量密度等于磁场能量密度。
例5.1.2 频率为9.4GHz的均匀平面波在聚乙烯中传播，设其为无耗 波长、波阻抗和电场强度的幅值。
材料，相对介电常数为εr = 2.26 。若磁场的振幅为7mA/m，求相速、 解：
1
v


c
r
3 108 1.996108 m / s 2.26
2 2 v k f
2
直角坐标系中均匀平面波沿z方向传播，则