磁路定理第三章(磁路设计)

磁路设计的基本概念第一章磁路电机是一种机电能量转换装置，变压器是一种电能传递装置,它们的工作原理都以电磁感应原理为基础，且以电场或磁场作为其耦合场。

在通常情况下，由于磁场在空气中的储能密度比电场大很多，所以绝大多数电机均以磁场作为耦合扬。

磁场的强弱和分布，不仅关系到电机的性能，而且还将决定电机的体积和重量；所以磁场的分析扣计箅，对于认识电机是十分重要的。

由于电机的结构比校复杂，加上铁磁材料的非线性性质，很难用麦克斯韦方程直接解析求解；因此在实际工作中．常把磁场问题简化成磁路问题来处理。

从工程观点来说，准确度已经足够。

本章先说明磁路的基本定律，然后介绍常用铁磁材料及其性能，最后说明磁路的计算方法。

1-1 磁路的基本定律一、磁路的概念磁通所通过的路径称为磁路。

图1—1表示两种常见的磁路，其中图a为变压器的磁路，图b为两极直流电机的磁路。

在电机和变压器里，常把线圈套装在铁心上。

当线圈内通有电流时、在线圈周围的空间(包括铁心内、外)就会形成磁场。

由于铁心的导磁性能比空气要好得多，所以绝大部分磁通将在铁心内通过，并在能量传递或转换过程中起耦合场的作用，这部分磁通称为主磁通。

围绕裁流线圈、部分铁心和铁心周围的空间，还存在少量分散的磁通，这部分磁通称为漏磁通。

主磁通和漏磁通所通过的路径分别构成主磁路和漏磁路，图1—l中示意地表出了这两种磁路。

用以激励磁路中磁通的载流线圈称为励磁线圈(或称励磁绕组)，励磁线圈中的电流称为励磁电流(或激磁电流)。

若励磁电流为直流，磁路中的磁通是恒定的，不随时间而变化，这种磁路称为直流磁路；直流电机的磁路就属于这一类。

若励磁电流为交流(为把交、直流激励区分开，本书中对文流情况以后称为激磁电流)，磁路中的磁通随时间交变变化，这种磁路称为交流磁路；交流铁心线圈、变压器和感应电机的磁路都属于这一类。

二、磁路的基本定律进行磁路分析和计算时，往往要用到以下几条定律。

安培环路定律沿着任何一条闭合回线L，磁场强度H的线积分值恰好等于该闭合回线所包围的总电流值∑i，(代数和)．这就是安培环路定律(图l—2)。

磁路及电感计算作者: 日期:第三章磁路和电感计算不管是一个空心螺管线圈，还是带气隙的磁芯线圈，通电流后磁力线分布在它周围的 整个空间。

对于静止或低频电磁场问题，可以根据电磁理论应用有限元分析软件进行求解， 获得精确的结果，但是不能提供简单的、指导性的和直观的物理概念。

在开关电源中，为 了用较小的磁化电流产生足够大的磁通 (或磁通密度)，或在较小的体积中存储较多的能量,经常采用一定形状规格的软磁材料磁芯作为磁通的通路。

因磁芯的磁导率比周围空气或其 他非磁性物质磁导率大得多，把磁场限制在结构磁系统之内，即磁结构内磁场很强，外面 很弱，磁通的绝大部分经过磁芯而形成一个固定的通路。

在这种情况下，工程上常常忽略 次要因素，只考虑导磁体内磁场或同时考虑较强的外部磁场，使得分析计算简化。

通常引 入磁路的概念，就可以将复杂的场的分析简化为我们熟知的路的计算。

3.1磁路的概念从磁场基本原理知道，磁力线或磁通总是闭合的。

磁通和电路中电流一样，总是在低 磁阻的通路流通，高磁阻通路磁通较少。

所谓磁路指凡是磁通(或磁力线)经过的闭合路径称为磁路。

3.2磁路的欧姆定律以图3.1(a)为例，在一环形磁芯磁导率为卩的磁芯上， 环的截面积A,平均磁路长度为I,绕有N 匝线圈。

在线圈中通入电流I ，在磁芯建立磁通，同时假定环的内径与外径相差很小，环的截面上磁通是均匀的。

根据式 (1.7)，考虑到式(1.1)和(1.3)有磁阻的单位在 SI 制中为安/韦，或1/亨；在CGS 制中为安/麦。

磁导的单位是磁阻单位 的倒数。

同理，在磁阻两端的磁位差称为磁压降Um,即(3.1)(3.2)表3.1磁电模拟对应关系U m= R m = BA X(3.4)引入磁路以后，磁路的计算服从于电路的克希荷夫两个基本定律。

根据磁路克希荷夫第一定律，磁路中任意节点的磁通之和等于零，即(3.5)根据安培环路定律得到磁路克希荷夫第二定律，沿某一方向的任意闭合回路的磁势的 代数和等于磁压降的代数和INR或INHI(3.6a)式(3.5)对应磁场的高斯定理，即穿过任何闭 合曲面的磁通之和为零。

磁路的基本定律磁路的基本定律磁路是指由铁芯和线圈组成的电器元件，在电机、变压器、电磁铁等电气设备中广泛应用。

学习磁路的基本定律对于理解和分析这些设备的工作原理具有重要意义。

一、磁通量1.1 磁通量的定义磁通量是指通过一个闭合曲面内部的总磁场线数，通常用字母Φ表示，单位为韦伯（Wb）。

1.2 磁通量的计算公式根据高斯定理，一个闭合曲面内部的总磁场线数等于该曲面上法向量方向上的磁感应强度积分。

因此，可以用以下公式计算：Φ = ∫B·dS其中，B为磁感应强度（单位为特斯拉），dS为曲面微元（单位为平方米），积分范围为该闭合曲面内部。

二、安培环路定理2.1 安培环路定理的定义安培环路定理是指在一个闭合回路上，沿着任意一条路径积分得到的电流总和相等。

即：∮H·dl = I其中，H为磁场强度（单位为安培/米），dl为路径微元（单位为米），I为该回路内的电流（单位为安培）。

2.2 安培环路定理的应用安培环路定理可以用于分析磁路中的磁通量和磁场强度之间的关系。

例如，在一个闭合回路上，如果有一段铁芯，那么根据安培环路定理，该铁芯内部的磁场强度H应该等于该回路内部电流I所产生的磁通量Φ与铁芯长度l之比。

即：H = Φ / l三、法拉第电磁感应定律3.1 法拉第电磁感应定律的定义法拉第电磁感应定律是指当一个闭合线圈中的磁通量发生变化时，会在线圈中产生感应电动势。

即：ε = -dΦ/dt其中，ε为感应电动势（单位为伏特），Φ为线圈内部的磁通量，t为时间。

3.2 法拉第电磁感应定律的应用法拉第电磁感应定律可以用于分析变压器、发电机等设备中的工作原理。

例如，在一个变压器中，当一侧线圈中的交流电流产生变化时，会在另一侧线圈中产生感应电动势，从而实现电能的传输和变换。

四、磁化曲线4.1 磁化曲线的定义磁化曲线是指在给定条件下，磁通量Φ和磁场强度H之间的关系。

通常用图表或曲线表示。

4.2 磁化曲线的特点磁化曲线的形态取决于铁芯材料的性质和工作状态。

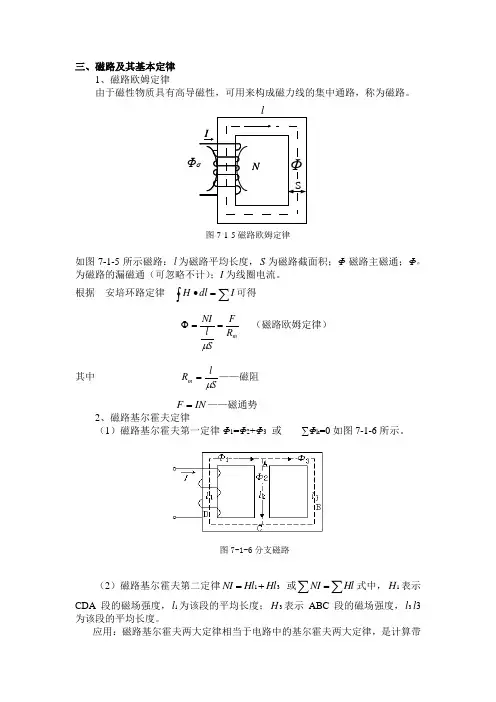
三、磁路及其基本定律1、磁路欧姆定律由于磁性物质具有高导磁性，可用来构成磁力线的集中通路，称为磁路。

Φ图7-1-5磁路欧姆定律如图7-1-5所示磁路：l 为磁路平均长度，S 为磁路截面积；Φ磁路主磁通；Φσ为磁路的漏磁通（可忽略不计）；I 为线圈电流。

根据 安培环路定律⎰∑=∙I dl H 可得m R FSl NI ==Φμ （磁路欧姆定律） 其中 SlR m μ=——磁阻 IN F =——磁通势 2、磁路基尔霍夫定律（1）磁路基尔霍夫第一定律Φ1=Φ2+Φ3 或 ∑Φk =0如图7-1-6所示。

（2）磁路基尔霍夫第二定律13NI Hl Hl =+ 或NI Hl =∑∑式中，1H 表示CDA 段的磁场强度，1l 为该段的平均长度；3H 表示ABC 段的磁场强度，3l l 3为该段的平均长度。

应用：磁路基尔霍夫两大定律相当于电路中的基尔霍夫两大定律，是计算带图7-1-6分支磁路有分支的磁路的重要工具(本书对并联磁路不作要求)。

（3）如表7-1所示为磁路和电路的类比关系：（1）电路中有电流就有功率损耗。

磁路中恒定磁通下没有功率损耗；（2）电流全部在导体中流动，而在磁路中没有绝对的磁绝缘体，除在铁心的磁通外，空气中也有漏磁通；（3）电阻为常数，磁阻为变量；（4）对于线性电路可应用叠加原理，而当磁路饱和时为非线形不能应用叠加原理。

综上所述磁路与电路仅是数学形式上的类似，而本质是不同的。

4、磁路的计算：图7-1-7对图7-1-7所示分段均匀磁路应用基尔霍夫第二定律有 IN H l H l H =++δ02211 或∑=IN Hl将 μBH S B =Φ=,代入，有IN SS l S l =+Φ+Φ0222111μδμμ 或 IN R R R m m m =Φ+Φ+Φ021∑∑=Φ=ΦmmR FFR式中μ不是常数，因此公式并不能用于计算磁路，只可做定性分析用。

在磁路的分析中若已知磁通Φ求所需磁通势IN 则 （1）由11S B Φ=（查H B -曲线）得出111l H H →； （2）由22S B Φ=（查H B -曲线）得出222l H H →； （3）由δμ0000100H B H S S B →=→Φ=Φ=； （4）∑=IN Hl对交流磁路则可按幅值进行分析，即： 已知→Φ=Φ=→ΦS K S B C m C m m m 查H B -曲线∑=→=→→2m m m m II N I l H H C K 为叠片系数。

磁路的基本概念和基本定律在很多电工设备（象变压器、电机、电磁铁等）中，不仅有电路的问题，同时还有磁路的问题，这一章，我们就学习磁的相关知识。

一、磁铁及其性质：人们把物体能够吸引铁、钴等金属及其合金的性质叫做磁性，把具有磁性的物体叫做磁体（磁铁）。

磁体两端磁性最强的区域叫磁极。

任何磁体都具有两个磁极，而且无论把磁体怎样分割总保持有两个异性磁极，也就是说，N极和S极总是成对出现的。

与电荷间的相互作用力相似，磁极间也存在相互的作用力，且同极性相互排斥，异极性相互吸引。

1．1磁场与磁感应线磁铁周围和电流周围都存在磁场。

磁场具有力和能的特征。

磁感应线能形象地描述磁场。

它们是互不交叉的闭合曲线，在磁体外部有N极指向S极，在磁体内部由S极指向N极，磁感应线上某点的切线方向表示该点的磁场方向，其疏密程度表示磁场的强弱。

1．2描述磁场的物理量：磁感应强度B：在磁场中垂直于磁场方向的通电导线所受电磁力F与电流I和导线有效长度L的乘积IL的比值即为该处的磁感应强度，即B＝F/IL，单位：特斯拉。

磁感应强度是表示磁场中某点磁场强弱和方向的物理量，它是一个矢量，它与电流之间的方向关系可用右手螺旋定则来确定。

磁通∮：磁感应强度B和与它垂直方向的某一截面积S的乘积，称为通过该面积的磁通，即∮＝BS，由上式可知，磁感应强度在数值上可以看作与磁场方向相垂直的单位面积所通过的磁通，故又称为磁通密度，单位是伏.秒，通常称为“韦”。

磁通∮是描述磁场在空间分布的物理量。

磁导率u是说明媒体介质导磁性能的物理量。

1．3定则电流与其产生磁场的方向可用安培定则（又称右手螺旋法则）来判断。

安培定则既适用于判断电流产生的磁场方向，也可用于在已知磁场方向时判断电流的方向。

1.直线电流产生的磁场，以右手拇指的指向表示电流方向，弯曲四指的指向即为磁场方向。

2.环形电流产生的磁场：以右手弯曲的四指表示电流方向，拇指所指的方向即为磁场方向。

3．通电导体在磁场内的受力方向，用左手定则来判断。

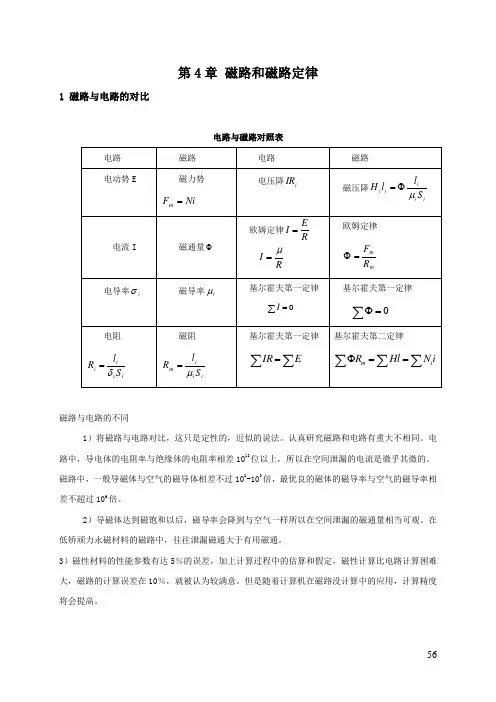
第4章磁路和磁路定律1 磁路与电路的对比电路与磁路对照表磁路与电路的不同1）将磁路与电路对比，这只是定性的，近似的说法。

认真研究磁路和电路有重大不相同。

电路中，导电体的电阻率与绝缘体的电阻率相差1013位以上，所以在空间泄漏的电流是微乎其微的。

磁路中，一般导磁体与空气的磁导体相差不过102-103倍，最优良的磁体的磁导率与空气的磁导率相差不超过106倍。

2）导磁体达到磁饱和以后，磁导率会降到与空气一样所以在空间泄漏的磁通量相当可观。

在低矫顽力永磁材料的磁路中，往往泄漏磁通大于有用磁通。

3）磁性材料的性能参数有达5％的误差，加上计算过程中的估算和假定，磁性计算比电路计算困难大，磁路的计算误差在10％，就被认为较满意。

但是随着计算机在磁路没计算中的应用，计算精度将会提高。

2 磁路的概念观察两种现象：a)在通电螺线管内腔的中部，电流产生的磁力线平行无螺线管的轴线，磁场线渐进螺线管两端时变成的散开的曲线，曲线在螺线管外部空间相接。

如果将一根长铁心插入通电螺线管中，并且让铁心闭合，则泄漏到空间的磁力线很少，由上，我们定义，不管有无铁心，磁力经过的路线，让我们成为磁路。

b)用永磁性作磁源，也产生上述现象。

图1 等效磁路图1 a)给出了永磁体单独存在时的情况。

图b)将永磁体放入软磁体回路的间隙中，磁力线的大部分通过软磁体和永磁体构成的回路。

以上两种也是表示磁回路。

图中磁力线密度表示磁通量的密度。

广义的讲，磁通量所通过的磁介质的路经叫磁路。

磁路是许多以电磁原理作成的机械、器件如电机，电器，磁电式仪表等的主要组成部分之一。

各种磁路传递着磁力线，发挥着应有的机能。

大多数磁路含有磁性材料和工作气隙，完全由磁性材料构成的闭合磁路的情况也有不少。

凡含有空隙的磁路，一部分磁通量作为有用磁场，还有一部分磁通量在空隙的附近泄漏在空间，形成漏磁通。

图2 磁路3磁路欧姆定律软磁圆环，截面积S 平均周长l 磁导率μ线圈匝N 电流为i 则圆环内的磁场H 为 :lNiH =(4-1) H 的方面与环的轴线平行。

1一. 磁荷法磁介质两种观点以及与电介质的对比二. 磁荷法和电流法的等效性三. 磁荷法的应用举例§6.4 磁荷法(简介)上次课回顾二. 静磁场中的唯一性定理三. 分区均匀各向同性介质中的静磁场介质界面与磁感应线重合/垂直§6.3 边值关系和唯一性定理2一. 磁路磁路定理i ri imi S l R 0μμ=磁阻:磁动势:0NI m =ε磁路定理:∑∑==imiB i i i m R l H φε二.磁路与电路对比磁阻的串联：21m m m R R R +=磁阻的并联：21111m m mR R R +=二.带电粒子在电磁场中运动的几个应用1. 磁聚焦和磁透镜2.回旋加速器3.霍尔效应及应用一.带电粒子在电磁场中的运动BE B E rvv v +均匀均匀均匀;;本次课主要内容§6.5 磁路定理§6.6 带电粒子在电磁场中的运动及几个应用无气隙时铁芯中的总磁通量以及该磁通量⎟⎟⎠⎞⎜⎜⎝⎛+S d S l r B 00'μμμφ气隙的磁位降磁介质中的磁位降10例十一. 电磁铁的设计.图示为一U 形电磁铁的磁路图.它的尺寸如下：磁极截面积,长度,磁导率轭铁截面积长度气隙长度在0--0.05 m 范围可调.如果线圈匝数N=5000,电流I 0最大为4A. 问:0.05m 和0.01m 时气隙磁场强度H 值各为多少？2101.0m S =m l 6.01=,60001=r μ,02.022m S =,40.12m l =,7002=r μ3l 2r μ1r μ根据磁路定理：30320221011S l S l S l NI r r B μμμμμφ++=磁极的磁位降轭铁的磁位降气隙的磁位降气隙中：)(330BS HS B ==μφ113322211130/S l S lS l S NI H r r ++=⇒μμ忽略漏磁效应，取21301.0mS S =≈Oe m A H 35109.4/1092.3×=×=时：m l 05.03=时：m l 01.03=Oem A H 46105.2/108.1×=×=结果表明：磁极靠得越近，则磁场越强上面的计算未考虑漏磁问题，计算结果比实际测量值偏大一些。