矢量分析 各种坐标系下梯度算符、拉普拉斯算符形式
- 格式:pdf
- 大小:300.94 KB
- 文档页数:9


第一章 矢量分析(说明:本章为07电本英语讲义的中译本)电磁场是矢量场,矢量分析是学习电磁场性质的基本数学工具之一。
本章中,我们主要介绍矢量场理论基本知识:矢量运算,标量场的梯度,矢量场的散度和旋度,以及对于矢量场运算有重要作用的称为戴尔(或那布拉)算符∇的运算规则。
稍后,将介绍狄拉克δ函数及一些重要的矢量场定理,它对我们今后学习电磁场理论有重要作用。
1-1 矢量运算我们在电磁场中遇到的大多数量可分为两类:标量和矢量。
仅有大小的量称为标量。
具有大小和方向的量称为矢量。
一矢量A 可写成A A =A e其中A 是矢量A 的大小,e A 是与A 同方向上的单位矢量。
矢量的大小称为矢量的模,单位矢量的模为1。
矢量A 方向上的单位矢量可以这样表示:A A=Ae 矢量将用黑斜体字母表示,单位矢量用e 来表示。
作图时,我们用一有长度和方向的箭头表示矢量,如图1-1-1所示。
如果两矢量A 和B 具有同样的大小和方向,它们是相等的。
如果两矢量A 和B 具有同样的物理的或几何的意义,则它们具有同样的量纲,我们可以对矢量进行比较。
如果一个矢量的大小为零,我们称为零矢量或空矢量。
这是唯一一个不能用箭头表示的矢量。
我们也可以定义面积矢量。
如果有一面积为s 的平面,则面积矢量s 的大小为s ,它的方向按右手螺旋规则确定,如图1-1-2所示。
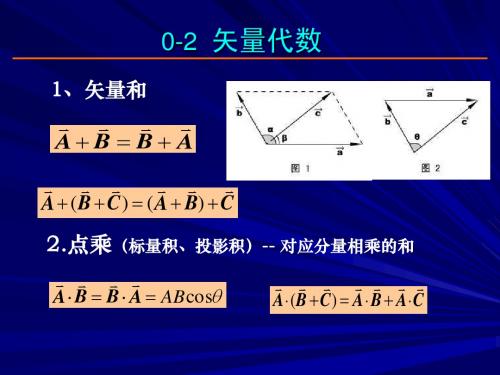
1-1-1 矢量加和减两矢量A 和B 可彼此相加,其结果给出另一矢量C ,C = A + B 。
矢量三角形或矢量四边形给出了两矢量A 和B 相加的规则,如图1-1-3所示。
由此我们可得出:矢量加法服从加法交换律和加法结合律。
交换律: A + B = B + A (1-1-1) 结合律:(A + B ) + C = A + (B + C ) (1-1-2)由C = A + B ,其也意味着一个矢量C 可以由两个矢量A 和B 来表示,即矢量C 可分解为两个分矢量A 和B (分量)。
也可说,一个矢量可以分解为几个分矢量。



有不少问题,由于边界的形状,不宜采用直角坐标系,而应采用球坐标系或柱坐标系等正交曲线坐标系。
在许多数学物理方程中,都用到拉普拉斯算符222222x y z∂∂∂∆=++∂∂∂。
采用正交曲线坐标系的时候,当然需要把拉普拉斯算符用正交曲线坐标表示出来。
“正交曲线坐标系中的拉普拉斯算符”在物理系高等数学教材中是有的。
但为了方便读者这里还是给出简单论述。
1、拉普拉斯算符作用于标量函数以123,,q q q 表示正交曲线坐标,则直角坐标与正交曲线坐标具有下列关系:()()()112233,,,,,,q q x y z q q x y z q q x y z ⎧=⎪=⎨⎪=⎩ ()()()123123123,,,,,,x x q q q y y q q q z z q q q ⎧=⎪=⎨⎪=⎩若两点具有相同的2q 和3q 而1q 相差微量1dq ,则两点间的距离为()()()()22221dz dy dx ds ++=()22221111x y z dq q q q ⎡⎤⎛⎫⎛⎫⎛⎫∂∂∂⎢⎥=++ ⎪ ⎪ ⎪∂∂∂⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,这可改写为111dq H ds =,1H (1)同理,若两点具有相同的3q 和1q 而2q 相差微量2dq ,则两点间的距离为222ds H dq =,2H (2)若两点具有相同的21,q q 而3q 相差微量3dq ,则两点间的距离为331dq H ds =,3H = (3)321,,H H H 叫做度规系数。
这样,标量函数()321,,q q q u 的梯度u ∇在1q 增长方向的分量为()11111q u H s u u ∂∂=∂∂=∇,从而()1111q u H u ∂∂=∇、()2221q u H u ∂∂=∇、()3331uu H q ∂∇=∂ (4) 再看矢量函数()321,,q q q A 。
取一个微小六面体,它由333222111,;,;,dq q q dq q q dq q q +++六个曲面围成(图1)。
向量算子 (nabla )表示向量微分算子。
】拉普拉斯算符梯度(标量化为矢量)散度(矢量化为标量)旋度(矢量化为矢量)数学解释在向量微积分中,标量场的梯度是一个向量场。
标量场中某一点上的梯度指向标量场增长最快的方向,梯度的长度是这个最大的变化率。
同时也可以求出变化不是最快的那个方向上的倒数,梯度点积该方向上的向量即可。
散度是向量分析中的一个向量算子,将向量空间上的一个向量场(矢量场)对应到一个标量场上。
散度描述的是向量场里一个点是汇聚点还是发源 点,形象地说,就是这包含这一点的一个微小体元中 的向量是“向外”居多还是“向内”居多。
旋度是向量分析中的一个向量算子,可以表示三维向量场对 某一点附近的微元造成的旋转程度。
这个向量提供了向量场在 这一点的旋转性质。
旋度向量的方向表示向量场在这一点附近旋转度最大的环量的旋转轴,它和向量旋转的方向满足右手定则。
拉普拉斯算子有许多用途,此外也是椭圆型算子中的 一个重要例子。
在物理中,常用于波方程的数学模型、热传导方程以 及亥姆霍兹方程。
在静电学中,拉普拉斯方程和泊松方程的应用随处可见。
在量子力学中,其代表薛定谔方程式中的动能项。
在数学中,经拉普拉斯算子运算为零的函数称为调和函 数;拉普拉斯算子是霍奇理论的核心,并且是德拉姆 上同调的结果。
物理解释考虑一座高度 点 的ft 。
这一 点的梯度是在该点坡度(或者说斜度)最陡的方向。
梯度的大小告诉我们坡度到底有多陡。
散度是通量的体密度物理上,散度的意义是场的有源性。
某一点或某个区域的散度大于零,表示向量场在这一点或这一区域有新的通量产生,小于零则表示向量场在这一点或区域有通量湮灭。
散度等于零的区域称为无源场或管形场。
就 的环量面密度(或称为环量强度)。
旋度是向量场的一种强度性质,就如同密度、浓度、温度一 样,它对应的广延性质是向量场沿一个闭合曲线的环量。
如果一个向量场中处处的旋度都是零,则称这个场为无旋场或保守场相关概念通环量记法=或三维直角坐标系柱坐标球坐标线性法则乘积法则商法则高斯散度定理:对某一个体积内的散度进行积分, 就应该得到这个体积内的总通量。
矢量分析与场论一、标量场的梯度,∇算符1、场的概念(The Concept of Field )场是用空间位置函数来表征的。
在物理学中,经常要研究某种物理量在空间的分布和变化规律。
如果物理量是标量,并且空间每一点都对应着该物理量的一个确定数值,则称此空间为标量场。
如:电势场、温度场等。
如果物理量是矢量,且空间每一点都存在着它的大小和方向,则称此空间为矢量场。
如:电场、速度场等。
若场中各点物理量不随时间变化,称为稳定场,否则,称为不稳定场。
2、方向导数(Directional Gradient )方向导数是标量函数)(x ϕ在空间一点沿任意方向l相对距离的变化率,它的数值与所取l 的方向有关。
一般来说,在不同的方向上lP l∂∂ϕ的值是不同的,但它并不是矢量。
如图所示,l为场中的任意方向,P 1是这个方向线上给定的一点,P 2为同一线上邻近的一点。
l ∆为p 2和p 1之间的距离,从p 1沿l到p 2的增量为)()(12p p ϕϕϕ-=∆若下列极限lp p l l l ∆-=∆∆→∆→∆)()(lim lim1200ϕϕϕ(1.1) 存在,则该极限值记作)(x ϕ,称之为标量场lP l∂∂ϕ在p 1处沿l的方向导P 1P 2l数。
3.梯度(Gradient )在某点沿某一确定方向取得)(xϕ在该点的最大方向导数。
n nˆgrad ∂∂=∇=ϕϕϕ (1.2) l l n n n l ⋅=⋅∂∂=∂∂=∂∂ϕϕϕθϕgrad ˆcos (1.3)4、∇算符(哈密顿算符)(Hamilton Functor )∇算符既具有微分性质又具有方向性质。
在任意方向l上移动线元距离dl ,ϕ的增量ϕd 称为方向微分,即l d dl ld ⋅∇=∂∂=ϕϕϕ (1.4)显然,任意两点ϕ值差为⎰⋅∇=-B AA B l dϕϕϕ (1.5)二、矢量场的散度、旋度、高斯定理和斯托克斯定理1、通量(Fluid )一个矢量场空间中,在单位时间内,沿着矢量场v 方向通过s d的流量是dN ,而dN 是以ds 为底,以v cos θ为高的斜柱体的体积,即s d v ds v dN⋅==θcos(1.6)称为矢量v 通过面元s d的通量。