下载文档原格式
⾼鸿业微观经济学习题及参考答案微观经济学习题参考答案中国⼈民⼤学出版社⾼鸿业《微观经济学》习题第⼆章需求与供给曲线概述以及有⼆、选择正确答案1.在得出某种商品的个⼈需求曲线时，下列（）外均保持为常数。
A.个⼈收⼊B.其余商品的价格C.个⼈偏好D.所考虑商品的价格2.在得出某棉花种植农户的供给曲线时，下列（）外均保持常数。
A.⼟壤的肥沃程度B.技术⽔平C.棉花的种植⾯积D.棉花的价格3.在某⼀时期内彩⾊电视机的需求曲线向左平移的原因可以是（）。
A.彩⾊电视机的价格上升B.⿊⽩电视机的价格上升C.消费者对彩⾊电视机的预期价格下降D.消费者的收⼊⽔平提⾼4.某⽉内，X商品的替代品的价格上升和互补品的价格上升，分别引起X商品的需求变动量为50单位和80单位，则在它们共同作⽤下该⽉X商品需求数量（）。
A.增加30单位B.减少30单位C.增加130单位D.减少130单位5.如果⼀条线性的需求曲线与⼀条曲线型的需求曲线相切，则在切点处两条需求曲线的需求的价格弹性系数（）。
A.不相同B.相同C．可能相同，也可能不相同 D.根据切点的位置⽽定6.消费者预期某物品未来价格要上升，则对该物品当前需求会（）。
A.减少B.增加C.不变D.上述三种都可能17.当两种商品中⼀种商品的价格发⽣变化时，这两种商品的需求量都同时增加或减少，则这两种商品的需求的交叉价格弹性系数为（）。
A.正B.负18.若X和Y两商品的交叉价格弹性是，则（）。
和Y是替代品和Y是正常商品和Y是劣等品和Y是互补品19.如果某商品富有需求的价格弹性，则该商品价格上升会使该商品的（）。
A.销售收益增加B.销售收益不变C.销售收益下降D.销售收益可能增加也可能下降答案：三、计算1.已知某⼀时期内某商品的需求函数为Q d=50-5P，供给函数为Q s=-10+5P。
（1）求均衡价格P e和均衡数量Q e。
（2）假定供给函数不变，由于消费者收⼊⽔平提⾼，使需求函数变为Q d=60-5P。
微观经济学重点概念1.需求消费者在一定时期内在各种可能的价格水平愿意而且能够购买的该商品的数量。
决定需求的因素一种商品的需求数量是由许多因素共同决定的。
其中的主要因素有：商品的价格、消费者的收入水平、相关商品的价格、消费者的偏好和消费者对该商品的价格预期等。
2.需求函数表示一种商品的需求数量和影响该需求数量的各种因素之间的相互关系的函数。
3.需求函数 需求函数()dQ f P =表示一种商品的需求量和该商品的价格之间存在着一一对应的关系。
4.商品的需求表商品的需求表是表示某种商品的各种价格水平和与各种价格水平相对应的该商品的需求数量之间的关系的数字序列表。
5.需求曲线的特征需求曲线具有一个明显的特征，它是向右下方倾斜的，即它的斜率是负值。
它们都表示水泥股票的需求量和价格之间呈反方向变动的关系。
6.供给生产者在一定时期内在各种价格水平下愿意并且能够提供出售的该种商品的数量。
7.供给函数供给函数表示一种商品的供给量和该商品的价格之间存在着一一对应的关系。
8.供给表商品的供给表表示某种商品的各种价格和与各种价格相对应的该商品的供给数量之间关系的数字序列表。
9.供给曲线的特征供给曲线表现出向右上方倾斜的特征，即供给曲线的斜率为正值。
它们都表示商品的供给量和价格成同方向变动的规律。
10. 均衡均衡的最一般的意义是指经济事物中有关的变量在一定条件的相互作用下所达到的一种相对静止的状态。
11. 均衡价格一种商品的均衡价格是指该种商品的市场需求量和市场供给量相等时的价格。
12. 均衡数量在均衡价格水平下的相等的供求数量被称为均衡数量。
市场上需求量与供给量相等的状态，也被称为市场出清状态。
13. 需求量的变动和需求的变动需求量的变动是指在其它条件不变时由某种商品的价格变动所应起的该商品需求数量的变动。
需求的变动是指在某商品价格不变的条件下，由于其它因素变动所引起的该商品需求数量的变动。
14. 供给量的变动和供给的变动供给量（点动）的变动是指在其它条件不变时由某种商品的价格变动所应起的该商品供给数量的变动。
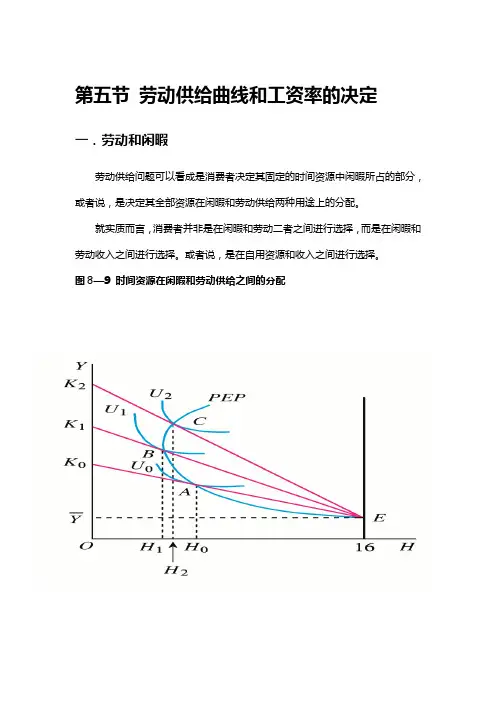
第五节劳动供给曲线和工资率的决定一．劳动和闲暇劳动供给问题可以看成是消费者决定其固定的时间资源中闲暇所占的部分，或者说，是决定其全部资源在闲暇和劳动供给两种用途上的分配。
就实质而言，消费者并非是在闲暇和劳动二者之间进行选择，而是在闲暇和劳动收入之间进行选择。
或者说，是在自用资源和收入之间进行选择。
图8—9 时间资源在闲暇和劳动供给之间的分配二．劳动供给曲线1.单个消费者的劳动供给曲线的得到随着劳动价格不断变化，则消费者的预算线将绕初始状态点顺时针或逆时针旋转，会得到众多的预算线分别与众多的无差异曲线的切点，从而能够确定均衡点所对应的最优闲暇量和相应的劳动供给量，最终得到单个消费者的劳动供给曲线。
图8—10 消费者的劳动供给曲线2.单个消费者的劳动供给曲线的特点单个消费者的劳动供给曲线有一段“向后弯曲”的部分。
当工资较低时，随着工资的上升，消费者为较高的工资吸引将减少闲暇，增加劳动供给量。
在这个阶段，劳动供给曲线向右上方倾斜。
但是，当工资上涨到很高时，消费者的劳动供给量达到最大。
此时如果继续增加工资，劳动供给量非但不会增加，反而会减少，于是劳动供给曲线开始向后弯曲。
三．替代效应和收入效应1.劳动供给是闲暇需求的反面在时间资源总量给定的条件下，劳动供给的增加就是闲暇需求的减少；反之亦然，即二者之间存在反方向变化关系。
2.劳动的价格即工资是闲暇的机会成本增加一单位时间的闲暇，意味着失去本来可以得到的一单位劳动的收入即工资。
于是，亦可以将工资看成是闲暇的价格。
3.对替代效应的分析闲暇的价格即工资上涨，于是，相对于其他商品而言，闲暇这个商品现在变得更加“昂贵”了（其机会成本上升了）。
于是消费者减少对它的“购买”，而转向其他替代商品。
因此，由于替代效应，闲暇需求量与闲暇价格反方向变化。
4.对收入效应的分析闲暇价格即工资的上升意味着实际收入的上升。
因为消费者此时享有同样的闲暇即提供同样的劳动量可以获得更多的收入。
第三章效用论◎ <该章的基本要求与基本知识点>◎ <教学重点与难点>◎ <第一节效用论概述>◎ <第二节无差异曲线>◎ <第三节预算线>◎ <第四节消费者的均衡>◎ <第五节价格变化和收入变化对消费者均衡的影响>◎ <第六节替代效应和收入效应>◎ <第七节从单个消费者的需求曲线到市场需求曲线>◎ <第八节不确定性和风险>◎ <本章小结 >※<该章的基本要求与基本知识点>（1）掌握效用、总效用、边际效用的含义；（2）会用图形描述总效用与边际效用的关系；（3）理解边际效用递减规律的含义；（4）掌握消费者均衡的公式，并会进行推导和证明；（5）了解无差异曲线的含义与特征；（6）了解消费者预算线的含义；（7）会用图形说明如何达到消费者均衡，以及计算消费者均衡；（8）会从消费者的均衡条件推导消费者的需求曲线；（9）掌握什么是替代和收入效应，并会用图形表示正常商品的替代效应和收入效应。
※<教学重点与难点>边际效用递减规律、消费者均衡、收入效应、替代效应※<第一节效用论概述>一、效应的概念效用是指商品满足人的欲望的能力，即消费者在消费商品时所感受到的满足程度。
效用是一种主观心理评价。
二、基数效用和序数效用基数效用论者认为，效用如同长度、重量等概念，可以具体衡量并加总求和。
效用的度量单位是“效用单位”。
基数效用论者用边际效用分析方法来研究消费者行为。
序数效用论者认为，效用如同香、臭、美、丑等概念，其大小无法具体衡量，效用之间的比较只能通过顺序或等级来表示。
序数效用论者用无差异曲线的分析方法来研究消费者行为。
三、基数效用论和边际效用分析方法概述基数效用论者区分了总效用和边际效用。
总效用和边际效用分别用TU 和MU 表示。
假定某消费者对某商品的消费量为Q，则总效用函数为：TU＝TU（Q）相应的边际效用为：或者由上式可知，每一商品数量上的边际效用值是总效用曲线的斜率。
