二次根式的化简与计算的策略与方法
- 格式:docx
- 大小:102.13 KB
- 文档页数:18

二次根式的化简与运算二次根式是指含有根号的代数表达式,通常是一种简化和运算方式,可以将复杂的表达式化简为简单的形式,并进行加减乘除等基本运算。
本文将介绍二次根式化简与运算的基本方法和技巧。
一、二次根式的化简1. 同底数的根式相加减:当根式的底数相同且指数相同时,可以直接对系数进行加减运算,保持根号不变。
例如:√2 + √2 = 2√22. 二次根式的有理化:当二次根式的底数是一个整数,但含有一个或多个根号时,可以通过有理化的方法化简。
例如:√(2/3) = (√2)/(√3) = (√2)/(√3) × (√3)/(√3) = √6/33. 二次根式的合并:当二次根式的底数相同,但系数不同时,可以合并为一个根式,将系数加在一起,并保持底数不变。
例如:3√2 + 2√2 = 5√24. 二次根式的分解:当二次根式的底数是一个整数,且无法进行合并时,可以进行分解,并找出其中可以合并的部分。
例如:√12 = √(4 × 3) = 2√3二、二次根式的运算1. 加减运算:当二次根式的底数和指数都相同时,可以直接对系数进行加减运算,保持底数和指数不变。
例如:2√5 + 3√5 = 5√52. 乘法运算:当二次根式相乘时,可以将根式的系数分别相乘,并保持底数和指数不变。
例如:2√3 × 3√2 = 6√63. 除法运算:当二次根式相除时,可以将根式的系数分别相除,并保持底数和指数不变。
例如:6√8 ÷ 2√2 = 3√24. 乘方运算:当二次根式进行乘方运算时,可以将指数分别应用到系数和根号上,并保持底数不变。
例如:(2√3)^2 = 2^2 × (√3)^2 = 4 × 3 = 12总结:二次根式的化简与运算是一种常见的数学操作,在代数表达式的计算中经常会遇到。
通过适当的化简和运算,可以简化复杂的根式,得到更加简单和规范的表达形式。
熟练掌握二次根式的化简和运算方法,有助于提高数学计算的效率和准确性。

人教版八年级下册数学 第16章 二次根式化简的方法和技巧1、被开放数是小数的二次根式化简例1、化简5.1分析:被开放数是小数时,常把小数化成相应的分数,后进行求解。
解:5.1=26262223232==⨯⨯=。
评注:化简时通常分子、分母同时乘以分数的分母,使分母上数或者式子成为完全平方数或者完全平方式。
2、被开放数是分数的二次根式化简例2、化简1251 分析:因为,125=5×5×5=52×5,所以,只需分子、分母同乘以5就可以了。
解:1251=255555551=⨯⨯⨯⨯。
评注:化简时,通常分子、分母同时乘以分数分母的一个恰当因数或因式,使分母上数或者式子成为完全平方数或者完全平方式。
3、被开放数是非完全平方数的二次根式化简例3、化简48分析:因为,48=16×3=42×3, 所以,根据公式b a ab ⨯=(a≥0,b≥0),就可以把积的是完全平方数或平方式的部分从二次根号下开出来,从而实现化简的目的。
解:48=34343163162=⨯=⨯=⨯。
评注:将被开放数进行因数分解,是化简的基础。
4、被开放数是多项式的二次根式化简例4、化简3)(y x +分析:当指数是奇数时,保持底数不变,设法把指数化成是一个偶数和一个奇数的积。
解:3)(y x +=y x y x y x y x y x y x ++=+⨯+=++)()()()(22。
评注:当多项式从二次根号中开出来的时候,一定要注意添加括号。
否则,就失去意义。
5、被开放数是隐含条件的二次根式化简例5、化简a a1-的结果是: A )a B )a - C )a - D )a --分析:含字母的化简,通常要知道字母的符号。
而字母的符号又常借被开方数的非负性而隐藏。
因此,化简时要从被开方数入手。
解:∵a a 1-有意义∴a1-≥0,∴-a >0 ∴原式=a a a a a a a a a a a a a a a a--=--=--=--=---=-||)())(()()(12故选(C )。

二次根式的计算和化简二次根式是指包含平方根的表达式。
在数学中,我们经常需要进行二次根式的计算和化简。
本文将介绍如何进行二次根式的计算和化简,并提供一些相关的例子和方法。
一、二次根式的计算二次根式的计算主要包括加减乘除四则运算和指数运算。
下面将分别介绍这些运算的方法。
1. 加减运算对于两个二次根式的加减运算,首先要确定根号下的数(即被开方数)是否相同。
如果相同,则可以直接对根号下的数进行加减运算,并保持根号不变。
如果根号下的数不同,则需要进行化简,使根号下的数相同,再进行加减运算。
例如,计算√3+ √5。
由于根号下的数不同,我们可以进行化简。
将√3与√5相加,得到√3 + √5。
这就是最简形式的结果,无法再进行化简。
2. 乘法运算对于两个二次根式的乘法运算,可以直接将根号下的数相乘,并保持根号不变。
例如,计算√3 × √5。
将根号下的数相乘,得到√15。
这就是最简形式的结果。
3. 除法运算对于两个二次根式的除法运算,可以将被除数与除数的根号下的数相除,并保持根号不变。
例如,计算√15 ÷ √3。
将根号下的数相除,得到√5。
这就是最简形式的结果。
4. 指数运算对于二次根式的指数运算,可以将指数应用于根号下的数,并保持根号不变。
例如,计算(√2)²。
将指数应用于根号下的数2,得到2。
因此,(√2)² = 2。
二、二次根式的化简化简二次根式的目的是使根号下的数尽量小。
下面将介绍一些常用的化简方法。
1. 提取公因数如果根号下的数可以被某个数整除,可以将其提取出来,并保持根号不变。
这是一种常见的化简方法。
例如,化简√16。
16可以被4整除,所以可以将16写成4×4,即√(4×4)。
继续化简,得到2×√4。
最后,我们得到2×2 = 4。
因此,√16 = 4。
2. 合并同类项如果有多个二次根式相加或相乘,可以合并同类项,使根号下的数相加或相乘。

二次根式的运算与化简二次根式是指形如√a的数,其中a是一个非负实数。
在数学中,我们经常需要对二次根式进行运算和化简。
本文将介绍二次根式的运算规则和化简方法。
一、二次根式的运算规则1. 加减运算当二次根式的被开方数相同时,可用下面的规则进行加减运算:√a ± √a = 2√a例如:√3 + √3 = 2√3当二次根式的被开方数不同时,无法进行加减运算,需要化简为最简形式:√a ± √b = √a ± √b例如:√2 + √3 无法化简2. 乘法运算二次根式的乘法运算可以按照下列规则进行:√a × √b = √(a × b)例如:√2 × √3 = √6乘法运算的一种特殊情况是平方运算:(√a)² = a例如:(√2)² = 23. 除法运算二次根式的除法运算可以按照下列规则进行:√a ÷ √b = √(a ÷ b)例如:√6 ÷ √2 = √3除法运算的一种特殊情况是倒数运算:1/√a = √a/ a例如:1/√2 = √2/2二、二次根式的化简方法1. 提取因子法当二次根式中有相同的因子时,可以使用提取因子的方法进行化简。
例如:√8 = √(4 × 2) = 2√22. 有理化分母法当二次根式的分母为二次根式时,可以使用有理化分母的方法进行化简。
例如:1/√2 = √2/2 (有理化分母为2)3. 合并同类项法当二次根式中出现相同的根数时,可以使用合并同类项的方法进行化简。
例如:√2 + √2 = 2√24. 化简最简形式当无法再进行其他化简方法时,二次根式已经达到最简形式。
例如:√7 无法化简以上是对二次根式的运算和化简方法的介绍。
掌握了这些方法,我们可以在解决数学问题时更加灵活地利用二次根式进行运算和化简,简化计算过程。
希望本文能对你有所帮助。

二次根式的化简与运算二次根式是数学中的重要概念之一,可以表示为形如√a的数。
在数学运算中,化简和运算是常见且基础的操作。
本文将介绍二次根式的化简和运算的方法和技巧。
一、二次根式的化简化简二次根式是指将一个二次根式表示为一个更简单的形式。
下面是常见的化简方法:1. 提取因子:当二次根式中存在可以开平方的因子时,可以进行提取因子的操作。
例如,√8可以化简为2√2,√18可以化简为3√2。
2. 合并同类项:二次根式中如果含有相同根号下的数,可以合并它们。
例如,√3+√5可以合并为√3+5,2√6-3√6可以合并为-√6。
3. 有理化分母:当二次根式的分母是一个二次根式时,需要进行有理化分母的处理。
有理化分母的方法是乘以一个合适的形式,使得分母变为一个有理数。
例如,对于√(2/3),可以通过乘以√3/√3的形式,得到√(6/9),即(√6)/3。
以上是化简二次根式的常见方法,通过运用这些方法,可以将复杂的二次根式化简为简单的形式,更便于计算和理解。
二、二次根式的运算在进行二次根式的运算时,常见的操作包括加法、减法、乘法和除法。
下面是二次根式运算的规则和示例:1. 加法和减法:当二次根式中的根号下的数相同,可以直接进行加法或减法。
例如,√2+2√2等于3√2,3√5-√5等于2√5。
2. 乘法:二次根式的乘法遵循根号下的数相乘,系数相乘的原则。
例如,√3*2√5等于2√15。
3. 除法:二次根式的除法遵循根号下的数相除,系数相除的原则。
例如,(3√2)/(2√3)等于(3/2)√(2/3)。
通过运用这些规则,可以进行二次根式的运算,得到最简形式的结果。
综上所述,二次根式的化简和运算是数学中的基础操作,掌握了这些方法和技巧,可以更好地理解和解决与二次根式相关的问题。
通过大量练习和实践,相信大家能够在二次根式的化简和运算中游刃有余,提高数学能力和解题水平。

二次根式解题的高效技巧与方法在数学学习过程中,我们常常会遇到解决二次根式的问题。
因此,了解二次根式解题的高效技巧和方法对于提高数学解题能力至关重要。
本文将重点介绍一些二次根式解题的实用技巧和方法,帮助你更高效地解决这类问题。
一、化简根式当我们遇到复杂的二次根式时,通常可以通过化简根式来简化问题,使其更易于处理。
以下是一些常用的化简根式的方法:1. 提取公因数:当根式内的各个项存在公因数时,可以通过提取公因数来化简根式。
例如,√8可以化简为2√2,因为8可以分解为2的平方乘以2。
2. 有理化分母:当根式的分母为根式时,可以通过有理化分母的方法来化简根式。
例如,将分母为√3的根式有理化分母,可以乘以√3/√3得到分母为3的根式。
3. 分解因式:对于一些含有多个项的根式,可以尝试将其分解为更简单的因式相乘形式。
通过分解因式,可以简化根式并更方便地进行计算。
二、使用二次根式的性质二次根式具有一些特殊的性质,灵活运用这些性质能够简化解题过程。
以下是一些常用的二次根式性质:1. 平方定理:(a+b)²=a²+2ab+b²。
当解题中遇到根式的平方形式时,可以利用平方定理将其展开,从而简化计算。
2. 合并同类项:类似于代数中合并同类项的做法,二次根式也能够进行合并同类项的操作。
比如,√2+√3和2√2-3√3就是合并同类项的例子。
3. 乘法公式:二次根式的乘法公式为√a * √b = √(ab)。
在解题过程中,可以利用乘法公式将不同的二次根式相乘,从而简化问题。
三、配方法解二次根式方程解二次根式方程是二次根式解题的常见形式之一。
使用配方法是解二次根式方程的常用技巧。
以下是配方法的基本步骤:1. 将二次根式方程变形为(a + b)的平方的形式,其中a和b为一次根式。
2. 利用平方定理展开得到二次根式方程的标准形式,即a² + b² +2ab = 原方程的右侧。
3. 通过比较系数,推导出a和b的值。

二次根式的化简与运算方法二次根式是指含有根号的算式,可以看作是根数和字母的组合。
化简二次根式是对根式进行简化,使得根号下的数变得更简洁。
而运算二次根式则是对含有二次根式的算式进行加减乘除等数学运算。
一、二次根式的化简方法二次根式的化简涉及到有理化的概念,有理化即通过变形将根式转换成有理数的操作。
下面将分别介绍三种常见的二次根式的化简方法。
1. 同底同指并简化当二次根式的根号下的数相同,指数相同时,可以进行合并并简化。
例如:√8 + √8 = 2√22√3 + 3√3 = 5√32. 有理化分母对于分母含有根号的二次根式,可以通过有理化的方法将其转化为有理数。
例如:1/√2 = √2/21/√3 = √3/33. 用有理数乘以二次根式可以使用有理数乘以二次根式进行化简。
例如:2√5 × 3√5 = 6√25 = 30二、二次根式的运算方法二次根式的运算涉及到加减乘除等数学运算,下面将分别介绍这几种运算方法。
1. 加减运算二次根式的加减运算需要先找到根号下的数相同的根式,然后根据正负号进行合并。
例如:√5 + √8 = √5 + 2√2 (不能合并)2√3 + 3√3 = 5√32. 乘法运算二次根式的乘法运算可以直接相乘。
例如:√5 × √2 = √103√3 × 2√3 = 6√9 = 6×3 = 183. 除法运算二次根式的除法运算可以通过有理化的方法转化为乘法。
例如:(√10) / (√5) = (√10) / (√5) × (√5) / (√5) = (√50) / 5 = 10/5 = 24. 指数运算对于含有二次根式的指数运算,可以将根式拆解成两个因数相同的根式。
例如:(√2) ^ 3 = (√2) × (√2) × (√2) = (√8) = 2√2结论二次根式的化简与运算方法在数学的学习中经常会用到,掌握了这些方法能够帮助我们更好地解决问题。

二次根式化简与计算的方法和技巧根式(或称为根号)是数学中一个重要的概念,在许多数学问题中都会涉及到根式的计算与化简。
在本文中,我将介绍一些二次根式化简与计算的方法和技巧。
一、根式的化简方法1.合并同类项:对于具有相同根号的根式,可以将它们合并为一个根式,并进行运算。
例如,√3+√2+√3=2√3+√22.有理化分母:当根式的分母为根号时,可以通过有理化分母将其转化为有理数。
有理化分母的方法有两种:一是乘以分子分母的共轭复数;二是进行分式的乘法和除法。
例如,√2/(√2+1)可以有理化分母得到(√2/(√2+1))*((√2-1)/(√2-1))=(√2-1)。
3.化简复数根式:对于具有复数根号的根式,可以使用以下性质进行化简:(1)√(-a)=i√a(其中i为虚数单位)(2) √(ab) = √a * √b(其中a和b为非负实数)4.有理数展开:对于一些特殊的根式,可以将其展开为有理数的形式。
例如,√5可以展开为√5=√(4+1)=√(2^2+1)=2√(1/4+1/2)=2√(3/4)=2√3/2=√3二、根式的计算技巧1.四则运算:根式可以进行加法、减法、乘法和除法等四则运算。
在进行四则运算时,需要进行化简和合并同类项的操作。
2.分解因式:对于一些具有完全平方数的根式,可以通过分解因式的方法进行计算。
例如,√12=√(4*3)=2√33.二次根式的乘除法:当进行二次根式的乘法或除法时,可以根据根式的性质进行相应的计算。
例如,√3*√5=√(3*5)=√15;√3/√2=(√3/√2)*(√2/√2)=√(3*2)/√2=√6/√2=√34.化简复杂根式:对于一些形式较为复杂的根式,可以使用分解因式、合并同类项、有理化分母等方法进行化简。
例如,√(6+√8)=√[(√2)^2+√8]=√[2+2√2]=√2*√(1+√2)。
5.平方差公式:当进行根式的乘法和除法时,可以利用平方差公式进行计算。

二次根式的化简与运算二次根式是指含有根号下的二次方程的数或算式。
化简与运算二次根式的主要目的是简化表达式,使其更加简洁和易于计算。
本文将介绍二次根式的化简方法和常见的运算规则,帮助读者更好地理解和应用二次根式。
一、二次根式的化简二次根式的化简是指将复杂的二次根式表达式简化为较为简单的形式。
下面列举了常见的化简方法和示例:1. 合并同类项当二次根式中的根号内的数值部分相同时,可以合并为一项。
例如:√9+√9 = 2√9(√9=3)2. 分解因式当二次根式中的数值部分可以分解为两个因式乘积时,可以进行因式分解后再进行化简。
例如:√12 = √(4×3) = √4×√3 = 2√33. 有理化分母当二次根式的分母有根号时,可以通过有理化分母的方法化简。
例如:1/√5 = (1/√5)×(√5/√5)= √5/5以上是常见的二次根式化简方法,通过运用这些方法,可以将复杂的二次根式表达式简化为简单的形式,便于计算和理解。
二、二次根式的运算二次根式的运算包括加减乘除四种基本运算。
下面将分别介绍这四种运算的规则和示例:1. 加法与减法若两个二次根式的根号内的数值部分相同,则可以直接相加或相减数值部分,并保持根号不变。
例如:√2 + √2 = 2√2 (根号内数值部分相同)√3 - √2 (根号内数值部分不同,无法直接化简)2. 乘法两个二次根式相乘时,可以将根号内的数值相乘,并将根号外的部分相乘。
例如:√2 × √3 = √(2×3) = √63. 除法两个二次根式相除时,可以将根号内的数值相除,并将根号外的部分相除。
例如:√6 ÷ √2 = √(6÷2) = √3通过上述运算方法,可以很方便地对二次根式进行加法、减法、乘法和除法的运算。
综上所述,二次根式的化简和运算是数学中重要的基础概念和技巧。
在学习和应用过程中,我们需要掌握化简方法和运算规则,灵活运用,以便更好地解决相关问题。

二次根式的化简及计算根式是一种特殊的数学表达式,其中包含了平方根、立方根等形式的根。
二次根式是指根式中包含有二次根号的表达式。
为了化简和计算二次根式,我们需要了解一些基本的化简规则和计算方法。
化简规则:1.同一根号之间,无法进行合并。
例如,√2+√3无法进一步化简。
2.同一根号下的项可以进行合并。
例如,√3+√3=2√33.分数根式中,可以将分子或分母中的二次根式进行有理化(去掉分母中的二次根号)。
有理化的方法是将分子和分母均乘以分母的共轭。
例如,√2/√3可以有理化为(√2/√3)×(√3/√3)=√6/34.分子中是二次根式时,可以将其化简为分数形式。
例如,√8可以化简为2√2计算方法:1.相同根号下的项可以进行加减运算。
例如,√2+√3=√2+√32.根号下可以进行乘法或除法运算。
例如,√2×√3=√6,√6/√2=√33.可以将二次根式化简为分数形式,然后进行计算。
例如,(√2+√3)/(√3+√2)=(√2+√3)/(√(2×3)+√(3×3))=(√2+√3)/(√6 +√9)=(√2+√3)/√6+(√2+√3)/√9=(√2+√3)/(√2×√3)+(√2+√3) /√3=(√2+√3)/√2+(√2+√3)=(√2+√3)/(√2)+(√2+√3)=√2+(√2+√3)=2√2+√3下面我们通过一些例子来进一步说明二次根式的化简和计算:例1:化简√18解:首先我们注意到18可以写成9×2,而9的平方根是3,所以√18=√(9×2)=√9×√2=3√2例2:计算√10×√40。
解:首先我们将40分解成4×10,然后可以写成√10×√(4×10)=√10×(√4×√10)=√10×2√10=2√10×√10=2√(10×10)=2√100=20。
二次根式的化简与运算规则在初等代数中,我们经常会遇到各种根式的化简与运算问题。
其中,二次根式(即包含平方根的式子)是一种常见形式。
在本文中,我们将介绍二次根式的化简方法和相应的运算规则。
一、二次根式的化简当我们遇到一个二次根式,想要化简它时,可以遵循以下方法:1. 化简平方根的因数如果二次根式中的平方根有因数,我们可以将其化简为一个不含平方根的数。
例如,√12可以化简为2√3。
2. 合并同类项如果二次根式中的多个平方根具有相同的根指数,并且它们的系数可以合并,我们可以将它们合并为一个平方根。
例如,3√2 + 2√2可以合并为5√2。
3. 分解平方根的积当二次根式中有平方根的积时,我们可以使用分解平方根的积的方法进行化简。
例如,√8可以分解为√4 * √2,即2√2。
4. 使用有理化方法当二次根式中存在分母为平方根的情况时,我们可以使用有理化方法进行化简。
例如,1/√3可以有理化为√3/3。
总之,在化简二次根式时,我们可以运用因式分解、合并同类项和有理化等方法,以将其化简为更简洁的形式。
二、二次根式的运算规则在对二次根式进行运算时,有以下几个基本的运算规则:1. 二次根式的加减运算当我们对二次根式进行加减运算时,需要保证相同根指数的平方根项相同。
例如,√5 + 2√3 - √5可以化简为2√3。
2. 二次根式的乘法运算当我们对二次根式进行乘法运算时,可以将它们的系数和根指数相乘,并将相同根指数的平方根项合并。
例如,2√3 * 3√2可以化简为6√6。
3. 二次根式的除法运算当我们对二次根式进行除法运算时,可以将分子和分母的系数和根指数相除,并将相同根指数的平方根项合并。
例如,(4√6)/(2√3)可以化简为2√2。
需要注意的是,在进行二次根式的运算时,可能会遇到需要化简的情况。
因此,在运用运算规则时,我们需要结合化简方法进行综合运算。
总结:二次根式的化简与运算是初等代数中的重要内容。
通过本文的介绍,我们了解了二次根式的化简方法,包括化简平方根的因数、合并同类项、分解平方根的积和有理化方法等。
二次根式的化简与运算二次根式是数学中常见的一类表达式,它可以通过化简和运算来得到简化形式。
在本文中,我们将探讨二次根式的化简和运算方法,以帮助读者更好地理解和应用这一概念。
一、二次根式的化简方法二次根式通常以√a的形式出现,其中a是非负实数。
下面我们介绍几种常见的二次根式化简方法。
1. 提取因子法当二次根式内部存在可以被完全开方的因子时,我们可以使用提取因子法进行化简。
例如,对于√12,我们可以提取出其中的公因子4,得到2√3。
2. 合并同类项法如果多个二次根式具有相同的根号内部表达式,我们可以通过合并同类项来简化它们。
例如,对于√2 + √8,我们可以合并为√2 + 2√2,然后化简为3√2。
3. 有理化分母法当二次根式的分母为根号时,我们需要对其进行有理化分母。
具体做法是将根号内部的表达式乘上一个合适的因式,使得分母变为有理数。
例如,对于1/√3,我们可以乘以√3/√3,得到√3/3。
二、二次根式的运算方法除了化简,我们还可以进行二次根式的运算,包括加减乘除。
下面我们将分别介绍这些运算的方法。
1. 加减运算对于两个二次根式的加减运算,我们首先要合并同类项,即将具有相同根号内部表达式的项合并在一起。
然后,根据需要进行化简,得到最简形式。
例如,对于√2 + 2√2,我们可以合并为3√2。
2. 乘法运算二次根式的乘法运算可以通过将两个二次根式相乘,然后化简得到最简形式。
例如,(2√3)(3√3) = 6√9 = 6×3 = 18。
3. 除法运算二次根式的除法运算可以通过将一个二次根式除以另一个二次根式,然后化简得到最简形式。
例如,(4√2)/(2√2) = 4/2 = 2。
三、例题演练为了更好地理解和掌握二次根式的化简与运算,我们来解决一些例题。
1. 化简√27并写成最简形式。
解:我们可以应用提取因子法,将27分解为3×3×3。
然后,提取其中的完全平方数因子,得到√(3×3×3) = 3√3。
二次根式的化简与计算的策略与方法二次根式是初中数学教学的难点内容,读者在掌握二次根式有关的概念与性质后,进行二次根式的化简与运算时,一般遵循以下做法:①先将式中的二次根式适当化简②二次根式的乘法可以参照多项式乘法进行,运算中要运用公式,③对于二次根式的除法,通常是先写成分式的形式,然后通过分母有理化进行运算.④二次根式的加减法与多项式的加减法类似,即在化简的基础上去括号与合并同类项.⑤运算结果一般要化成最简二次根式.化简二次根式的常用技巧与方法二次根式的化简是二次根式教学的一个重要内容,对于二次根式的化简,除了掌握基本概念和运算法则外,还要掌握一些特殊的方法和技巧,会收到事半功倍的效果,下面通过具体的实例进行分类解析.1.公式法例1计算①;②解①原式②原式解后评注以上解法运用了“完全平方公式”和“平方差公式”,从而使计算较为简便.2.观察特征法例2计算:方法导引若直接运用根式的性质去计算,须要进行两次分母有理化,计算相当麻烦,观察原式中的分子与分母,可以发现,分母中的各项都乘以,即得分子,于是可以简解如下:解原式.例3 把下列各式的分母有理化.1;2方法导引①式分母中有两个因式,将它有理化要乘以两个有理化因式那样分子将有三个因式相等,计算将很繁,观察分母中的两个因式如果相加即得分子,这就启示我们可以用如下解法:解①原式方法导引②式可以直接有理化分母,再化简.但是,不难发现②式分子中的系数若为“1”,那么原式的值就等于“1”了因此,②可以解答如下:解②原式3.运用配方法例4化简解原式解后评注注意这时是算术根,开方后必须是非负数,显然不能等于“”4.平方法例5化简解∵∴.解后评注对于这类共轭根式与的有关问题,一般用平方法都可以进行化简5.恒等变形公式法例6化简方法导引若直接展开,计算较繁,如利用公式,则使运算简化.解原式6.常值换元法例7化简解令,则:原式7.裂项法例8化简解原式各项分母有理化得原式例9化简方法导引这个分数如果直接有理化分母将十分繁锁,但我们不难发现每一个分数的分子等于分母的两个因数之和,于是则有如下简解:解原式8.构造对偶式法例10化简解构造对偶式,于是没,则,,原式9.由里向外,逐层化简解∵而∴原式解后评注对多重根式的化简问题,应采用由里向外,由局部到整体,逐层化简的方法处理.10.由右到左,逐项化简例11化简方法导引原式从右到左是层层递进的关系,因此从右向左进行化简.解原式.解后评注平方差公式和整体思想是解答本题的关键,由平方差公式将多重根号逐层脱去,逐项化简,其环节紧凑,一环扣一环,如果不具有熟练的技能是难以达到化简之目的的.返回二次根式大小比较的常用方法二次根式的化简具有极强的技巧性,而在不求近似值的情况下比较两个无理数即二次根式的大小同样具有很强的技巧性,对初中生来说是一个难点,但掌握一些常见的方法对它的学习有很大的帮助和促进作用.1.根式变形法例1比较与的大小解将两个二次根式作变形得,∵,∴即解后评注本解法依据是:当,时,①,则;②若,则2.平方法例2比较与的大小解,∵,∴解后评注本法的依据是:当,时,如果,则,如果,则.3.分母有理化法通过运用分母有理化,利用分子的大小来判断其倒数的大小.例3比较与的大小解∵又∵∴4.分子有理化法在比较两个无理数的差的大小时,我们通常要将其进行分子有理化,利用分母的大小来判断其倒数的大小.例4比较与的大小解∵又∵∴.而5.等式的基本性质法例5比较与的大小解法1∵又∴即解后评注本解法利用了下面两个性质:①都加上同一个数后,两数的大小关系不变.②非负底数和它们的二次幂的大小关系一致.解法2将它们分别乘以这两个数的有理化因式的积,得又∵∴解后评注本解法的依据是:都乘以同一个正数后,两数的大小关系不变.6.利用媒介值传递法例6比较与的大小解∵∴又∵∴∴解后评注适当选择介于两个无理数之间的媒介法,利用数值的传递性进行比较.7.作差比较法在对两数进行大小比较时,经常运用如下性质:①;②例7比较与的大小解∵∴8.求商比较法与求差比较法相对应的还有一种比较的方法,即作商比较法,它运用的是如下性质,当,时,则:①;②例8比较与的大小.解∵∴∴解后评注得上所述,含有根式的无理数大小的比较往往可采用多种方法,来求解.有时还需各种方法配合使用,其中根式变形法,平方法是最基本的,对于具体的问题要作具体分析,以求用最佳的方法解出正确的结果.二次根式的化简与计算的策略与方法二次根式是初中数学教学的难点内容,读者在掌握二次根式有关的概念与性质后,进行二次根式的化简与运算时,一般遵循以下做法:①先将式中的二次根式适当化简②二次根式的乘法可以参照多项式乘法进行,运算中要运用公式,③对于二次根式的除法,通常是先写成分式的形式,然后通过分母有理化进行运算.④二次根式的加减法与多项式的加减法类似,即在化简的基础上去括号与合并同类项.⑤运算结果一般要化成最简二次根式.化简二次根式的常用技巧与方法二次根式的化简是二次根式教学的一个重要内容,对于二次根式的化简,除了掌握基本概念和运算法则外,还要掌握一些特殊的方法和技巧,会收到事半功倍的效果,下面通过具体的实例进行分类解析.1.公式法例1计算①;②解①原式②原式解后评注以上解法运用了“完全平方公式”和“平方差公式”,从而使计算较为简便.2.观察特征法例2计算:方法导引若直接运用根式的性质去计算,须要进行两次分母有理化,计算相当麻烦,观察原式中的分子与分母,可以发现,分母中的各项都乘以,即得分子,于是可以简解如下:解原式.例3 把下列各式的分母有理化.1;2方法导引①式分母中有两个因式,将它有理化要乘以两个有理化因式那样分子将有三个因式相等,计算将很繁,观察分母中的两个因式如果相加即得分子,这就启示我们可以用如下解法:解①原式方法导引②式可以直接有理化分母,再化简.但是,不难发现②式分子中的系数若为“1”,那么原式的值就等于“1”了因此,②可以解答如下:解②原式3.运用配方法例4化简解原式解后评注注意这时是算术根,开方后必须是非负数,显然不能等于“”4.平方法例5化简解∵∴.解后评注对于这类共轭根式与的有关问题,一般用平方法都可以进行化简5.恒等变形公式法例6化简方法导引若直接展开,计算较繁,如利用公式,则使运算简化.解原式6.常值换元法例7化简解令,则:原式7.裂项法例8化简解原式各项分母有理化得原式例9化简方法导引这个分数如果直接有理化分母将十分繁锁,但我们不难发现每一个分数的分子等于分母的两个因数之和,于是则有如下简解:解原式8.构造对偶式法例10化简解构造对偶式,于是没,则,,原式9.由里向外,逐层化简解∵而∴原式解后评注对多重根式的化简问题,应采用由里向外,由局部到整体,逐层化简的方法处理.10.由右到左,逐项化简例11化简方法导引原式从右到左是层层递进的关系,因此从右向左进行化简.解原式.解后评注平方差公式和整体思想是解答本题的关键,由平方差公式将多重根号逐层脱去,逐项化简,其环节紧凑,一环扣一环,如果不具有熟练的技能是难以达到化简之目的的.返回二次根式大小比较的常用方法二次根式的化简具有极强的技巧性,而在不求近似值的情况下比较两个无理数即二次根式的大小同样具有很强的技巧性,对初中生来说是一个难点,但掌握一些常见的方法对它的学习有很大的帮助和促进作用.1.根式变形法例1比较与的大小解将两个二次根式作变形得,∵,∴即解后评注本解法依据是:当,时,①,则;②若,则2.平方法例2比较与的大小解,∵,∴解后评注本法的依据是:当,时,如果,则,如果,则.3.分母有理化法通过运用分母有理化,利用分子的大小来判断其倒数的大小.例3比较与的大小解∵又∵∴4.分子有理化法在比较两个无理数的差的大小时,我们通常要将其进行分子有理化,利用分母的大小来判断其倒数的大小.例4比较与的大小解∵又∵∴.而5.等式的基本性质法例5比较与的大小解法1∵又∴即解后评注本解法利用了下面两个性质:①都加上同一个数后,两数的大小关系不变.②非负底数和它们的二次幂的大小关系一致.解法2将它们分别乘以这两个数的有理化因式的积,得又∵∴解后评注本解法的依据是:都乘以同一个正数后,两数的大小关系不变.6.利用媒介值传递法例6比较与的大小解∵∴又∵∴∴解后评注适当选择介于两个无理数之间的媒介法,利用数值的传递性进行比较.7.作差比较法在对两数进行大小比较时,经常运用如下性质:①;②例7比较与的大小解∵∴8.求商比较法与求差比较法相对应的还有一种比较的方法,即作商比较法,它运用的是如下性质,当,时,则:①;②例8比较与的大小.解∵∴∴解后评注得上所述,含有根式的无理数大小的比较往往可采用多种方法,来求解.有时还需各种方法配合使用,其中根式变形法,平方法是最基本的,对于具体的问题要作具体分析,以求用最佳的方法解出正确的结果.二次根式大小比较的常用方法二次根式的化简具有极强的技巧性,而在不求近似值的情况下比较两个无理数即二次根式的大小同样具有很强的技巧性,对初中生来说是一个难点,但掌握一些常见的方法对它的学习有很大的帮助和促进作用.1.根式变形法例1比较与的大小解将两个二次根式作变形得,∵,∴即解后评注本解法依据是:当,时,①,则;②若,则2.平方法例2比较与的大小解,∵,∴解后评注本法的依据是:当,时,如果,则,如果,则.3.分母有理化法通过运用分母有理化,利用分子的大小来判断其倒数的大小.例3比较与的大小解∵又∵∴4.分子有理化法在比较两个无理数的差的大小时,我们通常要将其进行分子有理化,利用分母的大小来判断其倒数的大小.例4比较与的大小解∵又∵∴.而5.等式的基本性质法例5比较与的大小解法1∵又∴即解后评注本解法利用了下面两个性质:①都加上同一个数后,两数的大小关系不变.②非负底数和它们的二次幂的大小关系一致.解法2将它们分别乘以这两个数的有理化因式的积,得又∵∴解后评注本解法的依据是:都乘以同一个正数后,两数的大小关系不变.6.利用媒介值传递法例6比较与的大小解∵∴又∵∴∴解后评注适当选择介于两个无理数之间的媒介法,利用数值的传递性进行比较.7.作差比较法在对两数进行大小比较时,经常运用如下性质:①;②例7比较与的大小解∵∴8.求商比较法与求差比较法相对应的还有一种比较的方法,即作商比较法,它运用的是如下性质,当,时,则:①;②例8比较与的大小.解∵∴∴解后评注得上所述,含有根式的无理数大小的比较往往可采用多种方法,来求解.有时还需各种方法配合使用,其中根式变形法,平方法是最基本的,对于具体的问题要作具体分析,以求用最佳的方法解出正确的结果.。
二次根式化简的方法与技巧二次根式是初中数学教学的难点内容,读者在掌握二次根式有关的概念与性质后,进行二次根式的化简与运算时,一般遵循以下做法:①先将式中的二次根式适当化简②二次根式的乘法可以参照多项式乘法进行,运算中要运用公式③对于二次根式的除法,通常是先写成分式的形式,然后通过分母有理化进行运算.④二次根式的加减法与多项式的加减法类似,即在化简的基础上去括号与合并同类项.⑤运算结果一般要化成最简二次根式.化简二次根式的常用技巧与方法所谓转化:解数学题的常用策略。
常言道:“兵无常势,水无常形。
”我们在解千变万化的数学题时,常常思维受阻,怎么办?运用转化策略,换个角度思考,往往可以打破僵局,迅速找到解题的途径。
二次根式的化简是二次根式教学的一个重要内容,对于二次根式的化简,除了掌握基本概念和运算法则外,还要掌握一些特殊的方法和技巧,会收到事半功倍的效果,约分、合并是化简二次根式的两个重要手段,因此我们在化简二次根式时应想办法把题目转化为可以约分和和可以合并的同类根式。
现举例说明一些常见二次根式的转化策略。
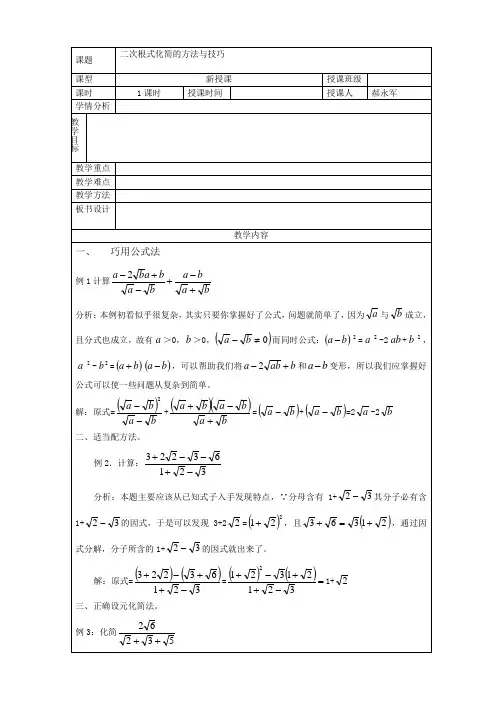
一、巧用公式法例1.计算分析:本例初看似乎很复杂,其实只要你掌握好了公式,问题就简单了,因为与成立,且分式也成立,故有而同时公式:可以帮助我们将和变形,所以我们应掌握好公式可以使一些问题从复杂到简单。
解:原式a2( a b)( a b) ba b a b( a b) ( a b)2 a 2 b二、适当配方法。
例 2.计算:分析:本题主要应该从已知式子入手发现特点,∵分母含有其分子必有含的因式,于是可以发现,且,通过因式分解,分子所含的的因式就出来了。
解:原式3 2 2 3 61 2 3(1 2 ) 2 3 (1 2 )1 2 31 2三、正确设元化简法。
例 3:化简分析:本例主要说明让数字根式转化成字母的代替数字化简法,通过化简替代,使其变为简单的运算,再运用有理数四则运算法则的化简分式的方法化简,例如:,正好与分子吻合。
二次根式化简求值的十种技巧下面是二次根式化简求值的十种技巧:技巧一:分解因式当二次根式的被开方数可以进行因式分解时,可以将其分解为两个或多个较简单的二次根式。
例如,√12可以分解为√4×√3,即2√3技巧二:有理化分母当二次根式的分母中含有二次根式时,可以采用有理化分母的方法进行化简。
有理化分母的方法是将分母有理化,即将分母中的二次根式进行去除。
例如,化简√(3/√2)时,可以将分母有理化为√(3×√2)。
技巧三:配方当二次根式中含有如(√x±√y)²或(√x±a)(√x±b)类型的项时,可以采用配方的方法进行化简。
例如,化简√(x+2√2+2)时,可以采用配方的方法,将其化简为(√(√2)+1)²。
技巧四:合并同类项当二次根式中含有相同的根号并且系数不同的项时,可以将其合并为一个项。
例如,化简√(2+√3)-√(2-√3)时,可以将两个相同根号下的项合并为一个项。
技巧五:有理数与二次根式相乘当二次根式与有理数相乘时,可以将二次根式中的根号与有理数相乘得到一个更简单的二次根式。
例如,化简2√8时,可以将其化简为2√(4×2),即4√2技巧六:有理数与二次根式相除当一个有理数与一个二次根式相除时,可以将有理数分子和二次根式的分母相除,并将其结果乘以二次根式的分子。
例如,化简2/√(3+√5)时,可以将其化简为2(√(3+√5))/((3+√5))。
技巧七:分子和分母进行有理化当一个二次根式作为一个分数的分子或分母时,可以将分子和分母同时进行有理化。
例如,化简√(5/√3)时,可以将其化简为(√5×√3)/√(3×√3),即(√15)/√3技巧八:提取公因式当一个二次根式中含有公因式时,可以将其提取出来,并进行分解或合并。
例如,化简√(6x+9)时,可以将其提取公因式3,并进行分解为3√(2x+3)。
二次根式的化简与分解技巧二次根式是数学中的一种特殊形式,通常表示为√a的形式,其中a 为非负实数。
在数学运算中,我们经常会遇到需要对二次根式进行化简或分解的情况。
本文将介绍一些常用的化简和分解技巧,帮助读者更好地应对这类问题。
一、二次根式的化简技巧1. 合并相同根号下的项当二次根式中有多个相同根号下的项时,可以将它们合并成一个。
例如:√3 + 2√3 = 3√32. 提取出最大平方因子当二次根式中存在一个或多个项可以写成完全平方数的形式时,可以将这些项分解成平方因子的乘积,并将其提取出来。
例如:√12 = √(4 × 3) = 2√33. 有理化分母当二次根式的分母为二次根式时,可以通过有理化分母的方法将其转化为有理数。
例如:1/√2 = (1/√2) × (√2/√2) = √2/2二、二次根式的分解技巧1. 平方差公式利用平方差公式,可以将二次根式分解成两个二次根式的差。
例如:√5 - √3 = (√5 - √3) × (√5 + √3) = 5 - 3 = 22. 公因式提取当二次根式中存在一个或多个因子相同的项时,可以将这些项提取出来,从而进行分解。
例如:√12 + √8 = 2√3 + 2√2 = 2(√3 + √2)3. 化简法对于复杂的二次根式,可以通过化简的方法将其转化为更简单的形式,进而进行分解。
例如:√(3+2√2) = √(√2)^2 + 2√2 = (√2 + 1)√2结语:二次根式的化简与分解技巧在数学中起到了重要的作用。
希望本文所介绍的内容能够帮助读者更好地理解和应用这些技巧,从而提高解题的能力。
在实际运用中,读者可以根据具体的题目要求和情况,灵活运用这些技巧,化繁为简,快速解决问题。
二次根式的化简与计算的策略与方法二次根式是初中数学教学的难点内容,读者在掌握二次根式有关的概念与性质后,进行二次根式的化简与运算时,一般遵循以下做法:①先将式中的二次根式适当化简②二次根式的乘法可以参照多项式乘法进行,运算中要运用公式(,)③对于二次根式的除法,通常是先写成分式的形式,然后通过分母有理化进行运算.④二次根式的加减法与多项式的加减法类似,即在化简的基础上去括号与合并同类项.⑤运算结果一般要化成最简二次根式.化简二次根式的常用技巧与方法二次根式的化简是二次根式教学的一个重要内容,对于二次根式的化简,除了掌握基本概念和运算法则外,还要掌握一些特殊的方法和技巧,会收到事半功倍的效果,下面通过具体的实例进行分类解析.1.公式法【例1】计算①;②【解】①原式②原式【解后评注】以上解法运用了“完全平方公式”和“平方差公式”,从而使计算较为简便.2.观察特征法【例2】计算:【方法导引】若直接运用根式的性质去计算,须要进行两次分母有理化,计算相当麻烦,观察原式中的分子与分母,可以发现,分母中的各项都乘以,即得分子,于是可以简解如下:【解】原式.【例3】把下列各式的分母有理化.(1);(2)()【方法导引】①式分母中有两个因式,将它有理化要乘以两个有理化因式那样分子将有三个因式相等,计算将很繁,观察分母中的两个因式如果相加即得分子,这就启示我们可以用如下解法:【解】①原式【方法导引】②式可以直接有理化分母,再化简.但是,不难发现②式分子中的系数若为“1”,那么原式的值就等于“1”了!因此,②可以解答如下:【解】②原式3.运用配方法【例4】化简【解】原式【解后评注】注意这时是算术根,开方后必须是非负数,显然不能等于“”4.平方法【例5】化简【解】∵∴.【解后评注】对于这类共轭根式与的有关问题,一般用平方法都可以进行化简5.恒等变形公式法【例6】化简【方法导引】若直接展开,计算较繁,如利用公式,则使运算简化.【解】原式6.常值换元法【例7】化简【解】令,则:原式7.裂项法【例8】化简【解】原式各项分母有理化得原式【例9】化简【方法导引】这个分数如果直接有理化分母将十分繁锁,但我们不难发现每一个分数的分子等于分母的两个因数之和,于是则有如下简解:【解】原式8.构造对偶式法【例10】化简【解】构造对偶式,于是没,则,,原式9.由里向外,逐层化简【解】∵而∴原式【解后评注】对多重根式的化简问题,应采用由里向外,由局部到整体,逐层化简的方法处理.10.由右到左,逐项化简【例11】化简【方法导引】原式从右到左是层层递进的关系,因此从右向左进行化简.【解】原式.【解后评注】平方差公式和整体思想是解答本题的关键,由平方差公式将多重根号逐层脱去,逐项化简,其环节紧凑,一环扣一环,如果不具有熟练的技能是难以达到化简之目的的.返回二次根式大小比较的常用方法二次根式的化简具有极强的技巧性,而在不求近似值的情况下比较两个无理数(即二次根式)的大小同样具有很强的技巧性,对初中生来说是一个难点,但掌握一些常见的方法对它的学习有很大的帮助和促进作用.1.根式变形法【例1】比较与的大小【解】将两个二次根式作变形得,∵,∴即【解后评注】本解法依据是:当,时,①,则;②若,则2.平方法【例2】比较与的大小【解】,∵,∴【解后评注】本法的依据是:当,时,如果,则,如果,则.3.分母有理化法通过运用分母有理化,利用分子的大小来判断其倒数的大小.【例3】比较与的大小【解】∵又∵∴4.分子有理化法在比较两个无理数的差的大小时,我们通常要将其进行分子有理化,利用分母的大小来判断其倒数的大小.【例4】比较与的大小【解】∵又∵∴.而5.等式的基本性质法【例5】比较与的大小【解法1】∵又∴即【解后评注】本解法利用了下面两个性质:①都加上同一个数后,两数的大小关系不变.②非负底数和它们的二次幂的大小关系一致.【解法2】将它们分别乘以这两个数的有理化因式的积,得又∵∴【解后评注】本解法的依据是:都乘以同一个正数后,两数的大小关系不变.6.利用媒介值传递法【例6】比较与的大小【解】∵∴又∵∴∴【解后评注】适当选择介于两个无理数之间的媒介法,利用数值的传递性进行比较.7.作差比较法在对两数进行大小比较时,经常运用如下性质:①;②【例7】比较与的大小【解】∵∴8.求商比较法与求差比较法相对应的还有一种比较的方法,即作商比较法,它运用的是如下性质,当,时,则:①;②【例8】比较与的大小.【解】∵∴∴【解后评注】得上所述,含有根式的无理数大小的比较往往可采用多种方法,来求解.有时还需各种方法配合使用,其中根式变形法,平方法是最基本的,对于具体的问题要作具体分析,以求用最佳的方法解出正确的结果.二次根式的化简与计算的策略与方法二次根式是初中数学教学的难点内容,读者在掌握二次根式有关的概念与性质后,进行二次根式的化简与运算时,一般遵循以下做法:①先将式中的二次根式适当化简②二次根式的乘法可以参照多项式乘法进行,运算中要运用公式(,)③对于二次根式的除法,通常是先写成分式的形式,然后通过分母有理化进行运算.④二次根式的加减法与多项式的加减法类似,即在化简的基础上去括号与合并同类项.⑤运算结果一般要化成最简二次根式.化简二次根式的常用技巧与方法二次根式的化简是二次根式教学的一个重要内容,对于二次根式的化简,除了掌握基本概念和运算法则外,还要掌握一些特殊的方法和技巧,会收到事半功倍的效果,下面通过具体的实例进行分类解析.1.公式法【例1】计算①;②【解】①原式②原式【解后评注】以上解法运用了“完全平方公式”和“平方差公式”,从而使计算较为简便.2.观察特征法【例2】计算:【方法导引】若直接运用根式的性质去计算,须要进行两次分母有理化,计算相当麻烦,观察原式中的分子与分母,可以发现,分母中的各项都乘以,即得分子,于是可以简解如下:【解】原式.【例3】把下列各式的分母有理化.(1);(2)()【方法导引】①式分母中有两个因式,将它有理化要乘以两个有理化因式那样分子将有三个因式相等,计算将很繁,观察分母中的两个因式如果相加即得分子,这就启示我们可以用如下解法:【解】①原式【方法导引】②式可以直接有理化分母,再化简.但是,不难发现②式分子中的系数若为“1”,那么原式的值就等于“1”了!因此,②可以解答如下:【解】②原式3.运用配方法【例4】化简【解】原式【解后评注】注意这时是算术根,开方后必须是非负数,显然不能等于“”4.平方法【例5】化简【解】∵∴.【解后评注】对于这类共轭根式与的有关问题,一般用平方法都可以进行化简5.恒等变形公式法【例6】化简【方法导引】若直接展开,计算较繁,如利用公式,则使运算简化.【解】原式6.常值换元法【例7】化简【解】令,则:原式7.裂项法【例8】化简【解】原式各项分母有理化得原式【例9】化简【方法导引】这个分数如果直接有理化分母将十分繁锁,但我们不难发现每一个分数的分子等于分母的两个因数之和,于是则有如下简解:【解】原式8.构造对偶式法【例10】化简【解】构造对偶式,于是没,则,,原式9.由里向外,逐层化简【解】∵而∴原式【解后评注】对多重根式的化简问题,应采用由里向外,由局部到整体,逐层化简的方法处理.10.由右到左,逐项化简【例11】化简【方法导引】原式从右到左是层层递进的关系,因此从右向左进行化简.【解】原式.【解后评注】平方差公式和整体思想是解答本题的关键,由平方差公式将多重根号逐层脱去,逐项化简,其环节紧凑,一环扣一环,如果不具有熟练的技能是难以达到化简之目的的.返回二次根式大小比较的常用方法二次根式的化简具有极强的技巧性,而在不求近似值的情况下比较两个无理数(即二次根式)的大小同样具有很强的技巧性,对初中生来说是一个难点,但掌握一些常见的方法对它的学习有很大的帮助和促进作用.1.根式变形法【例1】比较与的大小【解】将两个二次根式作变形得,∵,∴即【解后评注】本解法依据是:当,时,①,则;②若,则2.平方法【例2】比较与的大小【解】,∵,∴【解后评注】本法的依据是:当,时,如果,则,如果,则.3.分母有理化法通过运用分母有理化,利用分子的大小来判断其倒数的大小.【例3】比较与的大小【解】∵又∵∴4.分子有理化法在比较两个无理数的差的大小时,我们通常要将其进行分子有理化,利用分母的大小来判断其倒数的大小.【例4】比较与的大小【解】∵又∵∴.而5.等式的基本性质法【例5】比较与的大小【解法1】∵又∴即【解后评注】本解法利用了下面两个性质:①都加上同一个数后,两数的大小关系不变.②非负底数和它们的二次幂的大小关系一致.【解法2】将它们分别乘以这两个数的有理化因式的积,得又∵∴【解后评注】本解法的依据是:都乘以同一个正数后,两数的大小关系不变.6.利用媒介值传递法【例6】比较与的大小【解】∵∴又∵∴∴【解后评注】适当选择介于两个无理数之间的媒介法,利用数值的传递性进行比较.7.作差比较法在对两数进行大小比较时,经常运用如下性质:①;②【例7】比较与的大小【解】∵∴8.求商比较法与求差比较法相对应的还有一种比较的方法,即作商比较法,它运用的是如下性质,当,时,则:①;②【例8】比较与的大小.【解】∵∴∴【解后评注】得上所述,含有根式的无理数大小的比较往往可采用多种方法,来求解.有时还需各种方法配合使用,其中根式变形法,平方法是最基本的,对于具体的问题要作具体分析,以求用最佳的方法解出正确的结果.二次根式大小比较的常用方法二次根式的化简具有极强的技巧性,而在不求近似值的情况下比较两个无理数(即二次根式)的大小同样具有很强的技巧性,对初中生来说是一个难点,但掌握一些常见的方法对它的学习有很大的帮助和促进作用.1.根式变形法【例1】比较与的大小【解】将两个二次根式作变形得,∵,∴即【解后评注】本解法依据是:当,时,①,则;②若,则2.平方法【例2】比较与的大小【解】,∵,∴【解后评注】本法的依据是:当,时,如果,则,如果,则.3.分母有理化法通过运用分母有理化,利用分子的大小来判断其倒数的大小.【例3】比较与的大小【解】∵又∵∴4.分子有理化法在比较两个无理数的差的大小时,我们通常要将其进行分子有理化,利用分母的大小来判断其倒数的大小.【例4】比较与的大小【解】∵又∵∴.而5.等式的基本性质法【例5】比较与的大小【解法1】∵又∴即【解后评注】本解法利用了下面两个性质:①都加上同一个数后,两数的大小关系不变.②非负底数和它们的二次幂的大小关系一致.【解法2】将它们分别乘以这两个数的有理化因式的积,得又∵∴【解后评注】本解法的依据是:都乘以同一个正数后,两数的大小关系不变.6.利用媒介值传递法【例6】比较与的大小【解】∵∴又∵∴∴【解后评注】适当选择介于两个无理数之间的媒介法,利用数值的传递性进行比较.7.作差比较法在对两数进行大小比较时,经常运用如下性质:①;②【例7】比较与的大小【解】∵∴8.求商比较法与求差比较法相对应的还有一种比较的方法,即作商比较法,它运用的是如下性质,当,时,则:①;②【例8】比较与的大小.【解】∵∴∴【解后评注】得上所述,含有根式的无理数大小的比较往往可采用多种方法,来求解.有时还需各种方法配合使用,其中根式变形法,平方法是最基本的,对于具体的问题要作具体分析,以求用最佳的方法解出正确的结果.。