化工原理-第1章

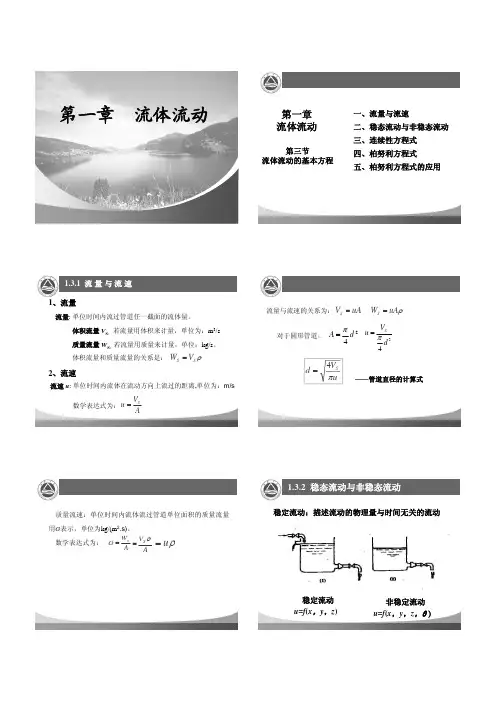
第一章流体流动第一章流体流动第三节流体流动的基本方程一、流量与流速二、稳态流动与非稳态流动三、连续性方程式四、柏努利方程式五、柏努利方程式的应用1.3.1 流量与流速1、流量流量: 单位时间内流过管道任一截面的流体量。

体积流量V S:若流量用体积来计量，单位为：m 3/s 质量流量W S:若流量用质量来计量，单位：kg/s 。

体积流量和质量流量的关系是：ρS S V W =2、流速流速u : 单位时间内流体在流动方向上流过的距离,单位为：m/s数学表达式为：AV u S =流量与流速的关系为：uAV S=ρuA W S =对于圆形管道，24dA π=24d V u S π=uV d S π4=——管道直径的计算式质量流速：单位时间内流体流过管道单位面积的质量流量用G 表示，单位为kg/(m 2.s)。

数学表达式为：A W G s =AV S ρ=ρu = 1.3.2 稳态流动与非稳态流动稳定流动：描述流动的物理量与时间无关的流动稳定流动u =f (x ，y ，z )非稳定流动u =f (x ，y ，z ，θ )1.3.2 稳态流动与非稳态流动流动系统稳态流动流动系统中流体的流速、压强、密度等有关物理量仅随位置而改变，而不随时间而改变非稳态流动上述物理量不仅随位置而且随时间变化的流动。

1.3.3 连续性方程在稳定流动系统中，对直径不同的管段做物料衡算衡算范围：取管内壁截面1-1’与截面2-2’间的管段。

衡算基准：1s对于连续稳定系统：21SSWW=ρuAWs=222111ρρAuAu=如果把这一关系推广到管路系统的任一截面，有：常数=====ρρρuAAuAuWS L222111若流体为不可压缩流体常数======uAAuAuWV SS L2211ρ——一维稳定流动的连续性方程对于圆形管道，22221144duduππ=21221⎟⎟⎠⎞⎜⎜⎝⎛=∴dduu表明：当体积流量VS一定时，管内流体的流速与管道直径的平方成反比。

化⼯原理第⼀章主要内容第⼀章流体流动流体：⽓体和液体统称流体。

流体的特点：具有流动性；其形状随容器形状⽽变化；受外⼒作⽤时内部产⽣相对运动。

质点：⼤量分⼦构成的集团。

第⼀节流体静⽌的基本⽅程静⽌流体的规律：流体在重⼒作⽤下内部压⼒的变化规律。

⼀、流体的密度ρ1. 定义：单位体积的流体所具有的质量，kg/m 3。

2. 影响ρ的主要因素液体：ρ=f(t)，不可压缩流体⽓体：ρ=f(t ，p)，可压缩流体3.⽓体密度的计算4.混合物的密度5.与密度相关的⼏个物理量⽐容υ⽐重(相对密度) d ⼆、压⼒p 的表⽰⽅法定义：垂直作⽤于流体单位⾯积上的⼒ 1atm=760mmHg=1.013×105Pa=1.033kgf/cm 2 =10.33mH2O 1at=735.6mmHg=9.807×105Pa =1kgf/cm 2 =10mH20 表压 = 绝对压⼒ - ⼤⽓压⼒真空度 = ⼤⽓压⼒ - 绝对压⼒三、流体静⼒学⽅程特点：各向相等性；内法线⽅向性；在重⼒场中，同⼀⽔平⾯上各点的静压⼒相等，但其值随着点的位置⾼低变化。

1、⽅程的推导 2、⽅程的讨论液体内部压强 P 随 P 0 和 h ⽽改变的； P ∝h ，静⽌的连通的同⼀种液体内同⼀⽔平⾯上各点的压强相等；当P 0改变时，液体内部的压⼒也随之发⽣相同的改变；⽅程成⽴条件为静⽌的、单⼀的、连续的不可压缩流体；h=(P-P 0)/ρg ，液柱⾼可表⽰压差，需指明何种液体。

3、静⼒学⽅程的应⽤ (1)压⼒与压差的测量 U 型管压差计微差压差计（2）液位的测定（3）液封⾼度的计算 m Vρ=(),f t p ρ=4.220M =ρ000T p p T ρρ=PM RT ρ=12121n m n a a a ρρρρ=+++1122......m n nρρ?ρ?ρ?=+++mm PM RTρ=1/νρ=41/,gh p p ρ+=0()12A C P P gR ρρ-=-() gz21A B A gR P P ρρρ+-=-第⼆节流体流动的基本⽅程⼀、基本概念（⼀）流量与流速1.流量：单位时间流过管道任⼀截⾯的流体量。

化工原理第一章总结化工原理是化学工程专业的重要基础课程，它为学生打下了坚实的理论基础，为日后的学习和工作奠定了基础。

在第一章中，我们主要学习了化工原理的基本概念、化学反应平衡和热力学基础等内容。

本文将对第一章的内容进行总结，希望能够帮助大家更好地理解和掌握这一部分知识。

首先，我们学习了化工原理的基本概念。

化工原理是研究化学工程中的基本原理和基本规律的学科，它包括物质的结构与性质、化学反应的基本原理、热力学基础等内容。

通过学习化工原理，我们可以更好地理解化学工程中的各种现象和过程，为日后的学习和工作打下坚实的基础。

其次，我们学习了化学反应平衡的相关知识。

化学反应平衡是化工原理中的重要内容，它描述了化学反应达到平衡时反应物和生成物的浓度之间的关系。

在学习中，我们了解了平衡常数的概念和计算方法，以及通过平衡常数来判断反应的方向和进行反应条件的优化等内容。

这些知识对于化学工程中的反应过程和工艺设计有着重要的指导作用。

最后，我们学习了热力学基础的相关内容。

热力学是研究能量转化和能量传递规律的学科，它在化工原理中占据着重要的地位。

在学习中，我们了解了热力学基本概念、热力学第一定律和第二定律等内容。

通过学习这些知识，我们可以更好地理解化学工程中的能量转化和传递过程，为工程实践提供理论支持。

综上所述，化工原理第一章主要介绍了化工原理的基本概念、化学反应平衡和热力学基础等内容。

通过学习，我们不仅对化工原理有了更深入的了解，也为日后的学习和工作打下了坚实的基础。

希望大家能够认真对待这门课程，努力学习，取得优异的成绩。

同时，也希望大家能够将所学知识应用到实际工程中，为化工行业的发展做出自己的贡献。

第一章流体流动1、密度定义: 单位体积流体所具有的质量称为密度.公式: ρ= m / V式中：ρ----流体的密度，kg/m3 ，m ----流体的质量，kg，V ----流体的体积，m3。

在研究流体流动时，若压力与温度变化不大时，则可认为液体的密度为常数。

密度为常数的流体称为不可压缩流体。

严格说来，真实流体都是可压缩流体，不可压缩流体只是在研究流体流动时，对于密度变化较小的真实流体的一种简化。

本章中如不加说明均指不可压缩流体。

2、气体密度一般来说气体是可压缩的，称为可压缩流体。

但是，在压力和温度变化率很小的情况下，也可将气体当作不可压缩流体来处理。

当气体的压力不太高，温度又不太低时，可近似按理想气体状态方程来计算密度。

即ρ= m /V＝nM / V = p M / RTp -------- 气体的绝对压强，kPa或kN/m2；n -------- 物质的量，mol ；M --------气体的摩尔质量，kg/mol；T -------- 气体的绝对温度，K；R ------气体常数，8.314 kJ/(kmol · K)。

3、混合物密度A. 液体混合物各组分的浓度常用质量分率来表示。

若混合前后各组分体积不变，则1kg混合液的体积等于各组分单独存在时的体积之和。

混合液体的平均密度ρm为：1/ρm =∑（xmi / ρi ）式中ρi------ 液体混合物中各纯组分的密度，kg/m3 ；xmi------ 液体混合物中各组分的质量分率。

B. 气体混合物各组分的浓度常用体积分率来表示。

若混合前后各组分的质量不变，则1m3混合气体的质量等于各组分单独存在时的质量之和。

混合气体的平均密度ρm为：ρm = ∑（xvi ρi ）式中ρi-------- 气体混合物中各纯组分的密度，kg/m3 ；xvi------ 气体混合物中各组分的体积分率。

二、流体的静压强1、静压强流体垂直作用于单位面积上的力，称为压强，或称为静压强。

化工原理第一章流体流动第一章 流体流动一、流体流动的数学描述在化工生产中，经常遇到流体通过管道流动这一最基本的流体流动现象。

当流体在管内作稳定流动时，遵循两个基本衡算关系式，即质量衡算方程式和机械能衡算方程式。

质量衡算方程式在稳定的流动系统中，对某一划定体积而言，进入该体积的流体的质量流量等于流出该体积的质量流量。

如图1—1所示，若取截面1—1′、2—2′及两截面间管壁所围成的体积为划定体积，则ρρρuA A u A u ==222111 (1-1a)对不可压缩、均质流体(密度ρ＝常数)的圆管内流动，上式简化为2221211ud d u d u == (1-1b)机械能衡算方程式在没有外加功的情况下，流动系统中的流体总是从机械能较高处流向机械能较低处，两处机械能之差为流体克服流动阻力做功而消耗的机械能，以下简称为阻力损失。

如图1—1所示，截面1—1′与2—2′间单位质量流体的机械能衡算式为f 21w Et Et += (1-2)式中 221111u p gz Et ++=ρ，截面1—1′处单位质量流体的机械能，J ／kg ；222222u p gz Et ++=ρ，截面2—2′处单位质量流体的机械能，J ／kg ；∑⎥⎦⎤⎢⎣⎡∑+∑=⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛∑+=2)(222f u d l l u d l w e λζλ，单位质量流体在划定体积内流动时的总阻力损失，J ／kg 。

其中，λ为雷诺数Re 和相对粗糙度ε / d 的函数，即⎪⎪⎭⎫ ⎝⎛=d du εμρφλ,。

上述方程式中，若将Et 1、Et 2、w f 、λ视为中间变量，则有z 1、z 2、p 1、p 2、u 1、u 2、d 1、d 2、d 、u 、l 、∑ζ(或∑l e )、ε、ρ、μ等15个变量，而独立方程仅有式(1-1)(含两个独立方程)、式(1-2)三个。

因此，当被输送流体的物性(ρ，μ)已知时，为使方程组有唯一解，还需确定另外的10个变量，其余3个变量才能确定。