讲义-2 原理
- 格式:pdf
- 大小:2.37 MB
- 文档页数:64

对于两个不同的分数,有分母相同,分子相同以及分子、分母都不相同三种情况,其中前两种情况判别大小的方法是:分母相同的两个分数,分子大的那个分数比较大;分子相同的两个分数,分母大的那个分数比较小。
第三种情况,即分子、分母都不同的两个分数,通常是采用通分的方法,使它们的分母相同,化为第一种情况,再比较大小。
由于要比较的分数千差万别,所以通分的方法不一定是最简捷的。
下面我们介绍另外几种方法。
1.“通分子”。
当两个已知分数的分母的最小公倍数比较大,而分子的最小公倍数比较小时,可以把它们化成同分子的分数,再比较大小,这种方法比通分的方法简便。
如果我们把课本里的通分称为“通分母”,那么这里讲的方法可以称为“通分子”。
2.根据倒数比较大小。
3.若两个真分数的分母与分子的差相等、则分母(子)大的分数较大;若两个假分数的分子与分母的差相等,则分母(子)小的分数较大。
分数混合运算式,要注意分数小数之间的互化,已达到简算的目的,同时考虑运算律的应用。
分数比较大小典型例题知识梳理【例1】★比较777773777778 和888884888889的大小。
【解析】这两个分数的分子与分母各不相同,不能直接比较大小,使用通分的方法又太麻烦。
由于这里的两个分数都接近1,所以我们可先用1分别减去以上分数,再比较所得差的大小,然后再判断原来分数的大小。
因为1-777773777778 =5777778 ,1-888884888889 =58888895777778 >5888889所以777773777778 <888884888889。
【小试牛刀】比较77777757777777 和66666616666663的大小。
【解析】77777757777777 >66666616666663【例2】★比较1111111 和111111111哪个分数大? 【解析】可以先用1分别除以这两个分数,再比较所得商的大小,最后判断原分数的大小。



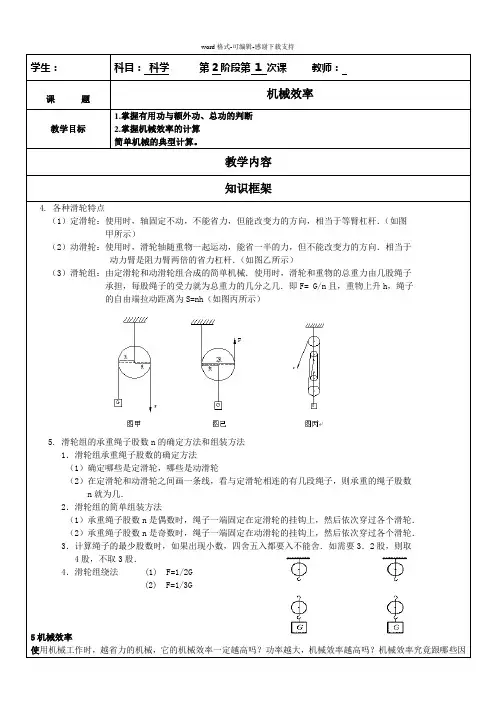
学生:科目:科学第2阶段第1 次课教师:课题机械效率教学目标1.掌握有用功与额外功、总功的判断2.掌握机械效率的计算简单机械的典型计算。
教学内容知识框架4. 各种滑轮特点(1)定滑轮:使用时,轴固定不动,不能省力,但能改变力的方向,相当于等臂杠杆.(如图甲所示)(2)动滑轮:使用时,滑轮轴随重物一起运动,能省一半的力,但不能改变力的方向.相当于动力臂是阻力臂两倍的省力杠杆.(如图乙所示)(3)滑轮组:由定滑轮和动滑轮组合成的简单机械.使用时,滑轮和重物的总重力由几股绳子承担,每股绳子的受力就为总重力的几分之几.即F= G/n且,重物上升h,绳子的自由端拉动距离为S=nh(如图丙所示)5. 滑轮组的承重绳子股数n的确定方法和组装方法1.滑轮组承重绳子股数的确定方法(1)确定哪些是定滑轮,哪些是动滑轮(2)在定滑轮和动滑轮之间画一条线,看与定滑轮相连的有几段绳子,则承重的绳子股数 n就为几.2.滑轮组的简单组装方法(1)承重绳子股数n是偶数时,绳子一端固定在定滑轮的挂钩上,然后依次穿过各个滑轮.(2)承重绳子股数n是奇数时,绳子一端固定在动滑轮的挂钩上,然后依次穿过各个滑轮. 3.计算绳子的最少股数时,如果出现小数,四舍五入都要入不能舍.如需要3.2股,则取4股,不取3股.4.滑轮组绕法 (1) F=1/2G(2) F=1/3G5机械效率使用机械工作时,越省力的机械,它的机械效率一定越高吗?功率越大,机械效率越高吗?机械效率究竟跟哪些因素有关?学完本节内容,你一定能回答这些问题.问:如何正确认识有用功、额外功和总功的含义及它们之间的关系? 问:机械效率总小于1吗?答:使用不同的机械做功,需要做的额外功各不相同,我们希望额外功在总功中所占的比例越小越好,或者说有用功在总功中所占比例越大越好.但由于额外功总是存在的,故有用功总是小于总功,所以,机械效率1%100<⨯=总有用W W η.问:如何比较机械效率的高低?答:机械效率由有用功和总功两个因素共同决定,比较机械效率高低时不能只考虑其中一个因素. 当总功一定时,机械做的有用功越多或额外功越少,机械效率就越高; 当有用功一定时,机械所做的总功越少或额外功越少,机械效率就越高;当额外功一定时,机械所做的总功越多或有用功越多,有用功在总功中所占的比例就越大,机械效率就越高. 问:关于机械效率,应注意哪些问题? 答:应注意以下几点:(1)机械效率η总小于1,因为W 有总小于W 总.(2)机械效率的高低取决于有用功和总功两个因素,不能理解成:“有用功多,机械效率高”;或“总功大,机械效率低”.(3)机械效率的高低与是否省力及大小无关.(4)机械效率不是固定不变的.机械效率反映的是机械在一次做功的过程中有用功跟总功的比值,同一机械在不同次做功的过程中,提起物重不同,机械效率往往会不同. (5)几种常见机械做功时机械效率的计算:G 表示物体的重力,F 表示作用在绳子自由端的拉力,h 表示物体上升的高度,s 表示对应物移动的距离 装 置 图滑轮组竖直提升重物杠杆提升重物滑轮组水平移动重物斜面提升重物W 有用 Gh G hfs 物GhW 总FsF SFs 绳Fsη Gh GFs nF=G h/ F Sfs f Fs nF=物绳GhFs(3).滑轮组公式:对于滑轮或滑轮组的拉力(F )或机械效率(η),一般分为三种状态: 滑轮组竖滑轮状态不记因素机械效率备注机 械 效 率 总功、额外功和有用功机械效率的定义及公式 探究斜面和滑轮组的机械效率芳芳的实验记较小提升速度 绳端拉 力(N ) 钩码重 (N ) 机械效率 较大提升速度 探究结10 4.2 79.4% 4.210物理量控制因素79.4%探究结果79.4%绳端拉 力(N ) 钩码重(N ) 机械 效率 大致相同的 提升速度 兰兰的实验记录10 4.2 156.0物理量 控制因素 直提升重物理想状态 即不计滑轮的重(G 动)、绳重(G 绳)、摩擦力(f )100% F= G 物/n S = n h 半理想状态 只计G 动,不计G 绳、f η= W 有/W 总 =G 物/(G 物+G 动) F= (G 物+G 动) /nS = n h实际状态计G 动、G 绳、fη= W 有/W 总 =G 物/n F S = n h 滑轮组水平重物\\η= W 有/W 总 =f/ n FS = n h题型一:对有用功、额外功、总功的认识,并能利用公式%100⨯=总有W W η进行简单的计算典型例题例1 一个工人用如图14-27所示的滑轮组提起2000N 的货物,所用的拉力是800N ,绳子自由端被拉下4m ,下列说法中正确的是 ( )A .总功是3200J ,机械效率是40%B .有用功是8000J ,机械效率是40%C .有用功是3200J ,机械效率是62.5%D .总功是3200J ,机械效率是62.5%例2 某人用如图14-28所示的滑轮组(不计摩擦力)提升某一重物,所用拉力F 为200N ,若滑轮组的机械效率为80%。

社会学讲义2第四章社会与社会运行●第一节社会●第二节社会运行第一节社会●一、什么是社会●1、“社会”的词源考察:本意为集会、聚会。
●中国古书中的“社会”●“社”就是一块地方的主人。
“会”就是集会。
两个字合起来就表示在一定的地方,于民间节日举行的演艺集会或祭神的庆祝活动。
后来发展为第二个意思,是指志趣相同者结合的团体。
●社会学中的“社会”●英文society的译语,来自于拉丁语socius一词。
●明治年间日本学者翻译society时借鉴中国文献中的“社会”一词,近代中国学者又沿用了这种译法。
●社会指的是由有一定联系、相互依存的人们组成的超乎个人的、有机的整体,它是人们的社会生活的体系。
●2、唯实论与唯名论●唯实论:社会是真实存在的实体,独立于个体之外且对个体构成实实在在的限制。
●代表人物:乔治·齐美尔,涂尔干。
●唯名论:只有个体才是客观存在的,社会只是一个概念,是人们的主观想像或抽象.●代表人物:吉丁斯,塔尔德。
●3.马克思主义论“社会”●社会是人们交往的产物,是各种社会关系的总和。
社会是人与人的关系以及人与自然的关系的统一。
●人的社会区别于动物社会的特征是劳动。
●人类社会是自然界长期发展的产物,人类社会是与自然界有重大区别的特殊领域。
●实践是社会的存在方式,社会在本质上是实践的。
●二、社会的特点●(1)社会是由人群组成的。
●(2)社会以人与人的交往为纽带。
●(3)社会是有文化、有组织的系统。
●(4)社会以人们的物质生产活动为基础。
●(5)社会系统具有心理的、精神的联系。
●(6)社会系统是一个具有主动性、创造性和改造能力的活的机体。
●三、社会的功能●(1)整合的功能。
●(2)交流的功能。
●(3)导向的功能。
●(4)继承和发展的功能。
●四、社会的类型●1.按生计方式来分(伦斯基)◆狩猎和采集社会◆游牧社会◆园耕社会◆农业社会◆工业社会●2、按社会关联的方式来分●滕尼斯(Tönnies):●礼俗社会(Gemeischaft)●法理社会(Gessellschaf)●涂尔干(Durkheim):●机械团结(mechanical solidarity)●有机团结(organic solidarity)●费孝通:团体格局与差序格局●差序格局: 是一个“一根根私人联系所构成的网络”。


1.4.2 微积分基本定理已知函数f (x )=2x +1,F (x )=x 2+x , 问题1:f (x ) 和F ′(x )有何关系? 提示:F ′(x )=f (x ).问题2:利用定积分的几何意义求⎠⎛02(2x +1)d x 的值. 提示:⎠⎛02(2x +1)d x =6. 问题3:求F (2)-F (0)的值. 提示:F (2)-F (0)=4+2=6.问题4:⎠⎛02(2x +1)d x 与F (2)-F (0)有什么关系? 提示:⎠⎛02f (x )d x =F (2)-F (0).1.微积分基本定理如果F ′(x )=f (x ),且f (x )在[a ,b ]上可积,则⎠⎛a bf (x )d x =F (b )-F (a ),其中F (x )叫做f (x )的一个原函数,由于[F (x )+c ]′=f (x ),F (x )+c也是f (x )的原函数,其中c 为常数.2.微积分基本定理的表示形式一般地,原函数在[a ,b ]上的改变量F (b )-F (a )简记作F (x )|b a ,因此,微积分基本定理可以写成形式:⎠⎛a bf (x )d x =F (x )|ba =F (b )-F (a ).1.微积分基本定理表明,计算定积分⎠⎛a bf (x )d x 的关键是找到满足F ′(x )=f (x )的函数F (x ),通常,我们可以运用基本初等函数的求导公式和导数的四则运算法则从反方向上求出F (x ).2.微积分基本定理揭示了导数与定积分之间的内在联系,最重要的是它也提供了计算定积分的一种有效方法.3.定积分的性质(1)⎠⎛a bkf (x )d x =k ⎠⎛a bf (x )d x (k 为常数);(2)⎠⎛a b [f 1(x )±f 2(x )]d x =⎠⎛a b f 1(x )d x ±⎠⎛a bf 2(x )d x ;[对应学生用书P28](3)⎠⎛a bf (x )d x =⎠⎛a cf (x )d x +⎠⎛c bf (x )d x (其中a <c <b ).[例1] 求下列定积分:(1)⎠⎛12(x 2+2x +3)d x ; (2)⎠⎛-π0 (cos x -e x )d x ;(3)⎠⎛2πsin 2x 2d x .[思路点拨] (1)(2)先求被积函数的原函数F (x ),然后利用微积分基本定理求解;(3)则需先对被积函数变形,再计算.[精解详析] (1)⎠⎛12(x 2+2x +3)d x =⎠⎛12x 2d x +⎠⎛122x d x +⎠⎛123d x=x 33|21+x 2|21+3x |21=253. (2)⎠⎛-π0(cos x -e x )d x =⎠⎛-π0cos x d x -⎠⎛-π0e x d x=sin x |0-π-e x |0-π=1e π-1.(3)sin 2x 2=1-cos x 2,而⎝⎛⎭⎫12x -12sin x ′=12-12cos x , ∴⎠⎛02πsin 2x 2d x =⎠⎛02π⎝⎛⎭⎫12-12cos x d x =⎝⎛⎭⎫12x -12sin x 02π=π4-12=π-24. [一点通]由微积分基本定理求定积分的步骤当被积函数为两个函数的乘积时,一般要转化为和的形式,便于求得函数F (x ),再计算定积分,具体步骤如下.[对应学生用书P28]第一步:求被积函数f (x )的一个函数F (x ); 第二步:计算函数的增量F (b )-F (a ).1.⎠⎛241x d x 等于( )A .-2ln 2B .2ln 2C .-ln 2D .ln 2解析:⎠⎛241x d x =(ln x )|42=ln 4-ln 2=ln 2. 答案:D2.计算下列定积分:(1)⎠⎛01(x 3-2x )d x ;(2)⎠⎛02π(x +cos x )d x ;(3)⎠⎛121x (x +1)d x .解:(1)⎠⎛01(x 3-2x )d x =⎝⎛⎭⎫14x 4-x 2|10=-34. (2)⎠⎛02π(x +cos x )d x =⎝⎛⎭⎫12x 2+sin x 02π=π28+1. (3)f (x )=1x (x +1)=1x -1x +1,取F (x )=ln x -ln (x +1)=ln xx +1, 则F ′(x )=1x -1x +1,所以⎠⎛121x (x +1)d x =⎠⎛12⎝⎛⎭⎫1x -1x +1d x =lnx x +1|21=ln 43.3.计算定积分⎠⎛03|x 2-1|d x .解:⎠⎛03|x 2-1|d x =⎠⎛01(1-x 2)d x +⎠⎛13(x 2-1)d x=⎝⎛⎭⎫x -13x 3|10+⎝⎛⎭⎫13x 3-x |31=223.4.已知f (x )=⎩⎨⎧4x -2π,x ∈⎣⎡⎦⎤0,π2,cos x ,x ∈⎝⎛⎦⎤π2,π.求定积分⎠⎛0πf (x )d x .解:⎠⎛0πf (x )d x =⎠⎛02πf (x )d x +⎠⎛2ππf (x )d x , 又(2x 2-2πx )′=4x -2π,(sin x )′=cos x ,所以⎠⎛02π(4x -2π)d x +⎠⎛2ππcos x d x =(2x 2-2πx )2π+sin x2ππ=π22-π2-0+0-1=-π22-1. ∴⎠⎛0πf (x )d x =-π22-1.[例2] 求抛物线y 2=2x 和直线y =-x +4所围成的图形的面积. [思路点拨] 结合图形,先求出两曲线的交点坐标.思路一:选x 为积分变量,将所求面积转化为两个积分的和求解; 思路二:选y 作积分变量,将所求面积转化为一个积分的计算求解.[精解详析] 先求抛物线和直线的交点,解方程组⎩⎪⎨⎪⎧y 2=2x ,y =-x +4,求出交点坐标为A (2,2)和B (8,-4).法一:选x 为积分变量,变化区间为[0,8],将图形分割成两部分(如图1),则面积为 S =S 1+S 2=2⎠⎛022x d x +⎠⎛28(2x -x +4)d x =423x 32|20+⎝ ⎛⎭⎪⎫223x 32-12x 2+4x |82 =18.图1 图2法二:选y 作积分变量,则y 的变化区间为[-4,2],如图2所求的面积为 S =⎠⎛-42⎝⎛⎭⎫4-y -y 22d y =⎝⎛⎭⎫4y -12y 2-16y 3|2-4 =18.[一点通] 利用定积分求由两条曲线围成的平面图形的面积的解题步骤: (1)画出图形.(2)确定图形范围,通过方程组求出交点的横坐标,确定积分上限和积分下限. (3)确定被积函数及积分变量,确定时可以综合考察下列因素:①被积函数的原函数易求;②较少的分割区域;③积分上限和积分下限比较简单. (4)写出平面图形的面积的定积分表达式.(5)运用微积分基本定理计算定积分,求出平面图形的面积.5.求曲线y =e x ,y =e -x 及直线x =1所围成的图形的面积.解:如图,由⎩⎪⎨⎪⎧y =e x,y =e -x ,解得交点为(0,1), 所求面积为S =⎠⎛01(e x -e -x )d x =(e x+e -x )|10=e +1e-2. 6.计算曲线y =x 2-2x +3与直线y =x +3所围成图形的面积.解:由⎩⎪⎨⎪⎧y =x +3,y =x 2-2x +3,解得x =0或x =3.如图.从而所求图形的面积S =⎠⎛03(x +3)d x -⎠⎛03(x 2-2x +3)d x =⎠⎛03[(x +3)-(x 2-2x +3)]d x=⎠⎛03(-x 2+3x )d x =⎝⎛⎭⎫-13x 3+32x 2⎪⎪⎪30=92.[例3] (12分)已知f (x )是二次函数,其图像过点(1,0),且f ′(0)=2,⎠0f (x )d x =0,求f (x )的解析式.[精解详析] 设f (x )=ax 2+bx +c (a ≠0), ∴a +b +c =0.①(2分) ∵f ′(x )=2ax +b , ∴f ′(0)=b =2.②(4分)∵⎠⎛01f (x )d x =⎠⎛01(ax 2+bx +c )d x=⎝⎛⎭⎫13ax 3+12bx 2+cx |10 =13a +12b +c =0.③(6分) 由①②③得⎩⎪⎨⎪⎧a =-32,b =2,c =-12,(10分)∴f (x )=-32x 2+2x -12.(12分)[一点通]含有参数的定积分问题的处理办法(1)含有参数的定积分可以与方程、函数或不等式综合起来考查,先利用微积分基本定理计算定积分是解决此类综合问题的前提.(2)计算含有参数的定积分,必须分清积分变量与被积函数f (x )、积分上限与积分下限、积分区间与函数F (x )等概念.7.(湖南高考)若⎠⎛0Tx 2d x =9,则常数T 的值为________.解析:∵⎠⎛0Tx 2d x =13T 3=9,T >0,∴T =3. 答案:38.设f (x )是一次函数,且⎠⎛01f (x )d x =5,⎠⎛01xf (x )d x =176,则f (x )的解析式为________. 解析:设f (x )=kx +b ,⎠⎛01f (x )d x =⎝⎛⎭⎫k 2x 2+bx |10=⎝⎛⎭⎫k 2+b -0=k 2+b , ⎠⎛01xf (x )d x =⎠⎛01(kx 2+bx )d x =⎝⎛⎭⎫k 3x 3+b 2x 2|10 =k 3+b 2. ∴⎩⎨⎧k2+b =5,k 3+b 2=176,∴⎩⎪⎨⎪⎧k =4,b =3.∴f (x )=4x +3.答案:f (x )=4x +39.已知f (x )=⎠⎛-a x(12t +4a )d t ,F (a )=⎠⎛01[f (x )+3a 2]d x ,求函数F (a )的最小值.解:∵f (x )=⎠⎛-a x(12t +4a )d t =(6t 2+4at )|x-a =6x 2+4ax -(6a 2-4a 2) =6x 2+4ax -2a 2,∴F (a )=⎠⎛01[f (x )+3a 2]d x =⎠⎛01(6x 2+4ax +a 2)d x=(2x 3+2ax 2+a 2x )|1=a 2+2a +2=(a +1)2+1≥1, ∴当a =-1时,F (a )最小值=1.1.求定积分的一些常用技巧: (1)对被积函数,要先化简,再求积分.(2)求被积函数是分段函数的定积分,依据定积分“对区间的可加性”,分段积分再求和.(3)对于含有绝对值符号的被积函数,要去掉绝对值符号后才能积分.2.在利用定积分求平面图形的面积时,要注意f (x )≥0的条件.当恒有f (x )<0时,定积分⎠⎛a bf (x )d x 为负值,从而曲边梯形的面积为⎠⎛a bf (x )d x 的相反数.1.(陕西高考)定积分⎠⎛01(2x +e x )d x 的值为( )A .e +2B .e +1C .eD .e -1解析:⎠⎛01(2x +e x )d x =(x 2+e x )10=(1+e)-(0+e 0)=e ,因此选C.答案:C2.设f (x )=⎩⎪⎨⎪⎧x 2,x ≥0,2x ,x <0,则⎠⎛-11f (x )d x 的值是( )A.⎠⎛-11x 2d x B.⎠⎛-112xd x C.⎠⎛-10x 2d x +⎠⎛012x d x D.⎠⎛-102x d x +⎠⎛01x 2d x 解析:⎠⎛-11f (x )d x =⎠⎛-102x d x +⎠⎛01x 2d x .答案:D3.(山东高考)直线y =4x 与曲线y =x 3在第一象限内围成的封闭图形的面积为( ) A .2 2 B .4 2 C .2D .4解析:由4x =x 3,解得x =0或x =2或x =-2(舍去),根据定积分的几何意义可知,直线y =4x 与曲线y =x 3在第一象限内围成的封闭图形的面积为⎠⎛02(4x -x 3)d x =⎝⎛⎭⎫2x 2-14x 4|20=4.[对应课时跟踪训练(十一)]答案:D4.若⎠⎛1a⎝⎛⎭⎫2x +1x dx =3+ln 2,则a 的值是( ) A .6 B .4 C .3D .2解析:⎠⎛1a⎝⎛⎭⎫2x +1x d x =(x 2+ln x )|a1=(a 2+ln a )-(1+ln 1)=(a 2-1)+ln a =3+ln 2.∴⎩⎪⎨⎪⎧a 2-1=3,a >1,a =2,∴a =2.答案:D5.(江西高考)计算定积分⎠⎛-11(x 2+sin x )d x =________.解析:⎠⎛-11(x 2+sin x )d x =⎝⎛⎭⎫x 33-cos x |1-1=23. 答案:236.由y =x 2,y =14x 2及x =1围成的图形的面积S =________.解析:图形如图所示:S =⎠⎛01x 2d x -⎠⎛0114x 2d x =⎠⎛0134x 2d x =14x 3|10=14. 答案:147.计算下列定积分:(1)⎠⎛-2-1(2+x 2)2d x ;(2)3ππ⎰cos ⎝⎛⎭⎫x -π6d x ;(3)⎠⎛-4 0|x +3|d x .解:(1)因为(2+x 2)2=4+4x 2+x 4, 又⎝⎛⎭⎫4x +43x 3+15x 5′=4+4x 2+x 4, 所以⎠⎛-2-1(2+x 2)2d x =⎠⎛-2-1(4+4x 2+x 4)d x=⎝⎛⎭⎫4x +43x 3+15x 5|-1-2 =⎝⎛⎭⎫-4-43-15-⎝⎛⎭⎫-8-323-325 =29315. (2)因为cos ⎝⎛⎭⎫x -π6=32cos x +12sin x , 所以3ππ⎰cos ⎝⎛⎭⎫x -π6d x =3ππ⎰⎝⎛⎭⎫32cos x +12sin x d x =323ππ⎰cos x d x +123ππ⎰sin x d x =32sin x 3ππ-12cos x 3ππ=-32sin π3-12⎝⎛⎭⎫cos π-cos π3 =-34+12+14=0.(3)因为f (x )=|x +3|=⎩⎪⎨⎪⎧-x -3,x <-3,x +3,x ≥-3,所以⎠⎛-40|x +3|d x =⎠⎜⎛-4-3(-x -3)d x +⎠⎛-30(x +3) d x=⎝⎛⎭⎫-12x 2-3x --34+⎝⎛⎭⎫12x 2+3x |0-3=5.8.在曲线y =x 2(x ≥0)上的某点A 处作一切线使之与曲线以及x 轴所围图形的面积为112.求切点A 的坐标以及切线方程.解:由题意可设切点A 的坐标为(x 0,x 20),则切线方程为y =2x 0x -x 20,可得切线与x 轴的交点坐标为⎝⎛⎭⎫x 02,0.画出草图,可得曲线y =x 2,直线y =2x 0x -x 20与x 轴所围图形如图所示.故S =S 1+S 2 =020x ⎰x 2d x +[02x x ⎰x 2d x -02x x ⎰ (2x 0x -x 20)d x ]高中数学课程11 =13x 3020x +13x 3002x x -(x 0x 2-x 20x ) 002x x=x 3012=112, 解得x 0=1,所以切点坐标为A (1,1), 所求切线方程为y =2x -1.。
ProtelDXP2004讲义(二)电路原理图设计基础一、电路原理图的设计知识进行电子电路设计时,首先要有一个设计方案,而将电路设计方案表达出来的最好方法就是画出清晰、正确的电路原理图。
同时,利用电路原理图还可以进行各种仿真分析。
1.电路原理图的设计过程根据设计需要选择出元器件,并把所选用的元器件和相互之间的连接关系明确地列出,直观地表达出设计概念。
2.电路原理图的基本组成就是电子元器件符号和连接导线,电子元器件符号包含了该元器件的功能,连接导线则包含了元器件的电气连接信息。
电路原理图设计的质量好坏直接影响到PCB印刷电路板的设计质量。
3.电路原理图绘制的原则(1)应该保证整个电路原理图的连线正确,信号流向清晰,便于阅读分析和修改。
(2)应该做到元器件的整体布局合理、美观、实用。
4.绘制电路原理图的步骤(1)启动DXP原理图编辑器,新建电路原理图文件。
(2)设置原理图的相关参数,如图纸的大小、版面及环境参数等(3)加载元件库,在图纸上放置需要的各种元器件。
(4)编辑元器件的属性,并对元器件进行合理的布局调整。
(5)使用导线或网络标签对所有的元器件进行电气意义上的连接。
(6)对电路原理图进行整体的编辑、调整。
(7)保存文档,打二、原理图编辑环境1.创建新原理图文件DXP系统采用了以项目为中心的设计环境,在一个项目中,文件与文件之间互有联系,当项目被编辑后,项目中的电路原理图文件或PCB印刷电路板文件的任何改变都会被同步更新。
所以,在创建新的原理图文件时,应首先创建一个新的PCB项目,然后将所创建的新的原理图文件添加到该项目中。
创建方法:(1)首先选择合适的保存路径,建立一个属于该项目的文件夹,用于专门存放和管理该项目所有的相关设计文件。
例如:在“D:\”下面建立一个文件夹“XXX”。
(2)创建一个新的PCB项目。
执行菜单命令【文件】→【创建】→【项目】→【PCB项目】,在【Projects】面板上,系统自动创建了一个默认名为“PCB-Project1.PrjPCB”的项目,执行项目命令菜单中的【另存项目为】命令,将其存为自己喜欢或者与设计项目有关的名字。
机械原理讲义第一章绪论机器特征:一、多个构件人为组合而成二、构件间具有确定的相对运动三、能减轻或代替人类的劳动或者实现能量的转换同时具备三个特征的即为机器,具备前两个特征的为机构;机构可以是一个零件也可以是多个零件的刚性组合。
第二章机构的结构分析基本要求:1、掌握机构运动简图的绘制方法。
2、掌握运动链成为机构的条件.3、熟练掌握机构自由度的计算方法。
4、掌握机构的组成原理和结构分析的方法。
重点:1、机构具有确定运动的条件.2、机机构运动简图及其绘制。
3、机构自由度的计算.难点:1、机构运动简图的绘制。
2、正确判别机构中的虚约束。
本章口诀诗:活杆三乘有自由,两低一高减中求;认准局复虚约束,简式易记考无忧。
本章作业:2-8(要求用五个方案改进)、2-10、2-12、2-142-15(a)、2-16(b)、2-17、2-19§2-1 平面机构运动简图一、机构及其组成1、机构的两大类型:平面机构、空间机构2、机构的两组成要素:①构件②运动副3、构件类型:①活动构件②固定构件(又称机架)二、运动副及其分类1、活动构件的自由度与约束自由度:作为独立运动单元可能的独立运动数约束:对物体运动自由度的限制2、运动副及其分类定义:构件间的可动联接。
类型:高副、低副。
三、平面机构运动简图1、定义及意义定义:用简单的线条和规定符号分别代表构件和运动副、用以表示各构件之间相对位置和相互运动关系的图形。
意义:方便进行运动学和动力学分析,便于技术出差时很快画出你所感兴趣的机器或机构的结构与运动特点。
2、绘制步骤从原动件开始、顺藤摸瓜(构件为藤,运动副为瓜)依次用线条和符号表示之(按尺寸比例)。
总结:低副产生两个约束即限制两个自由度。
高副,限制沿公法线方向的移动,但可沿切向移动和绕接触点转动。
§2-2 平面机构自由度计算一、平面机构具有确定运动的条件1、平面机构自由度公式的推导N个构件,1个机架,n=N-1为活动件数低副包括移动副和转动副自由度计算公式: F=3n—2Pl—Ph2、机构具有确定运动的条件:机构的原动件数等于机构的自由度数;F≥1二、自由度计算时的注意事项:1、认准复合铰链、局部自由度和虚约束1)复合铰链:多构件在同一处用回转副联接时,真正的回转副个数等于构件数—1。
数字电子技术实验讲义万用表及实验箱使用一、万用表使用重点讲解:1、电压和电阻测量2、“HOLD”数据保持按钮3、自动关闭功能4、用完后关闭电源二、示波器的使用由学生阅读示波器使用手册完成1、校准和选择探头(P)2、观察输入信号并调出稳定波形3、精确测量输入信号的幅度、周期和频率三、实验箱的构成1、电源开关2、电源输出:要求测量数据3、数据开关:可输出高低电平。
要求测量数据。
4、逻辑开关:可输出单次脉冲。
要求测量数据。
5、元件区:介绍集成块引脚识别、判断集成块是否插好。
6、电平指示:7、数码显示8、拨码开关:9、导线:要求判断通断四、使用注意事项1、导线插拨方法2、接线和更改线路一定要关闭电源3、注意观察电源指示灯,如接通电源时指示灯变暗,说明接线有短路,应关闭电源实验课的目的是培养学生的电子电路实验研究能力,培养学生理论联系实际的能力。
使学生能根据实验结果,利用所学理论,通过分析找出内在联系。
从而对电路参数进行调整,使之符合性能要求。
在实验中培养1.正确使用常用电子仪器。
2.3.4.5.6.7.能独立写出严谨的、有理论分析的、实事求是的、文理通顺、字迹端正的实验报为了顺利完成实验任务,确保人身、设备安全,培养严谨、踏实、实事求是的科学作风和爱护国家财产的优秀品质,特制1.1.1 认真阅读实验指导书,分析、掌握实验电路的工作原理,并进行必要的估算。
1.21.31.42.使用仪器、设备前必须了解其性能、操作方法及注意事项,在使用时应严格遵守。
3.实验时接线要认真,相互仔细检查,确信无误才能接通电源。
初学或没有把握时应经指导教师审查同意后才能接通电源。
4.实验时应注意观察,若发现有破坏性异常现象(例如有元件冒烟、发烫或有异味),应立即关断电源,保持现场,报告指导教师。
找出原因、排除故障并经指导教师同意才能再继续实验。
如果发生事故(例如元件或设备损坏)应主动填写实验事故报告单,服从实验室和指导教师对事故的处理决定(包括经济赔偿)5.6.实验过程中应仔细观察实验现象,认真记录实验结果(数据、波形及其现象)。