计算机图形学实验报告-二维裁剪

专业班级：学号：姓名：一、试验名称:二维裁剪二、试验目的：在二维观察中，需要在观察坐标系下对窗口进行裁剪，即只保留窗口内的那部分图形，去掉窗口外的图形。

二维裁剪是用计算机生成图形最基本的技能，通过本实验使学生掌握如何用计算机进行二维裁剪并熟悉开发环境。

三、实验原理：算法源代码：void CMyView::OnDraw(CDC* pDC){CMyDoc* pDoc = GetDocument();ASSERT_VALID(pDoc);// TODO: add draw code for native data herePoint FrameLT,FrameRB;Point P[5];FrameLT.x=150;FrameLT.y=150;FrameRB.x=320;FrameRB.y=320;pDC->Rectangle((int)FrameLT.x,(int)FrameLT.y,(int)FrameRB.x,(int)FrameRB. y);for(int i = 0; i < 5; i++){P[i].x = (float)(260 + 150*cos(72*i*PI/180) +0.5);P[i].y = (float)(260 + 150*sin(72*i*PI/180) +0.5);}专业班级：学号：姓名：pDC->MoveTo((int)P[0].x,(int)P[0].y);pDC->LineTo((int)P[2].x,(int)P[2].y);pDC->LineTo((int)P[4].x,(int)P[4].y);pDC->LineTo((int)P[1].x,(int)P[1].y);pDC->LineTo((int)P[3].x,(int)P[3].y);pDC->LineTo((int)P[0].x,(int)P[0].y);}void CMyView::Code(Point FrameLT,Point FrameRB,Point P,unsigned char *Flag){unsigned char flag=0;if(P.x<FrameLT.x) flag+=1;if(P.x>FrameRB.x) flag+=2;if(P.y>FrameRB.y) flag+=4;if(P.y<FrameLT.y) flag+=8;(*Flag)=flag;}void CMyView::Clipping(Point FrameLT,Point FrameRB,Point LineSP,Point LineEP){CClientDC dc(this);unsigned char flagSP,flagEP,flagAND,flagOR;double k=(LineEP.y-LineSP.y)/(LineEP.x-LineSP.x);Code(FrameLT,FrameRB,LineSP,&flagSP);Code(FrameLT,FrameRB,LineEP,&flagEP);专业班级：学号：姓名：flagAND=flagSP & flagEP;if(flagAND!=0)return;while(flagSP!=0||flagEP!=0){flagOR=flagSP|flagEP;if((flagOR&0x01)==1){if((flagSP&0x01)==1){LineSP.y=(float)(LineSP.y+k*(FrameLT.x-LineSP.x)); LineSP.x=FrameLT.x;Code(FrameLT,FrameRB,LineSP,&flagSP);}else{LineEP.y=(float)(LineEP.y+k*(FrameLT.x-LineEP.x)); LineEP.x=FrameLT.x;Code(FrameLT,FrameRB,LineEP,&flagEP);}}if((flagOR&0x02)==2){if((flagSP&0x02)==2){LineSP.y=(float)(LineSP.y+k*(FrameRB.x-LineSP.x)); LineSP.x=FrameRB.x;专业班级：学号：姓名：Code(FrameLT,FrameRB,LineSP,&flagSP);}else{LineEP.y=(float)(LineEP.y+k*(FrameRB.x-LineEP.x)); LineEP.x=FrameRB.x;Code(FrameLT,FrameRB,LineEP,&flagEP);}}if((flagOR&0x04)==4){if((flagSP&0x04)==4){LineSP.x=(float)(LineSP.x+(FrameRB.y-LineSP.y)/k); LineSP.y=FrameRB.y;Code(FrameLT,FrameRB,LineSP,&flagSP);}else{LineEP.x=(float)(LineEP.x+(FrameRB.y-LineEP.y)/k); LineEP.y=FrameRB.y;Code(FrameLT,FrameRB,LineEP,&flagEP);}}if((flagOR&0x08)==8){专业班级：学号：姓名：if((flagSP&0x08)==8){LineSP.x=(float)(LineSP.x+(FrameLT.y-LineSP.y)/k); LineSP.y=FrameLT.y;Code(FrameLT,FrameRB,LineSP,&flagSP);}else{LineEP.x=(float)(LineEP.x+(FrameLT.y-LineEP.y)/k); LineEP.y=FrameLT.y;Code(FrameLT,FrameRB,LineEP,&flagEP);}flagAND=flagSP&flagEP;if(flagAND!=0)return;}dc.MoveTo((int)LineSP.x,(int)LineSP.y);dc.LineTo((int)LineEP.x,(int)LineEP.y);}}void CMyView::OnCut() //裁剪{// TODO: Add your command handler code hereCClientDC dc(this);CPen pen(PS_SOLID,1,RGB(255,255,255));CPen *pOldpen = dc.SelectObject(&pen);专业班级：学号：姓名：CBrush*pBrush=CBrush::FromHandle((HBRUSH)GetStockObject(NULL_BRUSH));dc.SelectObject(pBrush);Point FrameLT,FrameRB;Point P[5];FrameLT.x=150;FrameLT.y=150;FrameRB.x=320;FrameRB.y=320;dc.Rectangle((int)FrameLT.x,(int)FrameLT.y,(int)FrameRB.x,(int)FrameR B.y);for(int i = 0; i < 5; i++){P[i].x = (float)(260 + 150*cos(72*i*PI/180) +0.5);P[i].y = (float)(260 + 150*sin(72*i*PI/180) +0.5);}dc.MoveTo((int)P[0].x,(int)P[0].y);dc.LineTo((int)P[2].x,(int)P[2].y);dc.LineTo((int)P[4].x,(int)P[4].y);dc.LineTo((int)P[1].x,(int)P[1].y);dc.LineTo((int)P[3].x,(int)P[3].y);dc.LineTo((int)P[0].x,(int)P[0].y);dc.SelectObject(pOldpen);专业班级：学号：姓名：dc.Rectangle((int)FrameLT.x,(int)FrameLT.y,(int)FrameRB.x,(int)FrameR B.y);Clipping(FrameLT,FrameRB,P[0],P[2]);Clipping(FrameLT,FrameRB,P[2],P[4]);Clipping(FrameLT,FrameRB,P[4],P[1]);Clipping(FrameLT,FrameRB,P[1],P[3]);Clipping(FrameLT,FrameRB,P[3],P[0]);}四、实验总结：裁剪处理的主要步骤是:①图元关于窗口内外关系的判别；②图元与窗口的求交。

计算机图形学中的二维裁剪算法研究计算机图形学研究的是如何在计算机上制图，根据研究对象的不同又分为二维图形学和三维图形学。

二维图形学研究的范畴是点，线，面。

本文就是介绍计算机图形学中的众多基本算法之一的二维剪裁算法。

在二维剪裁算法中，椭圆形窗口线剪裁算法又是应用最为广泛的算法之一，所以将是本文重点论述的对象。

标签：计算机图形学；二维剪裁算法；椭圆形窗口线剪裁算法计算机图形学中的基本算法对于计算机图形学应用于实践有着重要的作用，而且算法需要时时更新才能够发挥出计算机图形学在实践中的作用。

本文对计算机二维剪裁算法进行介绍，并对其中的椭圆窗口线剪裁算法进行着重的研究分析，探讨如何使该算法更加的稳定高效，方便易行。

算法可以指导人们的工作与生活，所以笔者在本文通过坐标分析设计出一个算法以供读者参考。

1 二维剪裁算法的基本介绍剪裁算法是计算机图形学中的基础算法之一。

剪裁在日常生活和工作中的应用十分广泛，最典型的一个应用就是对整体场景中的局部目的物进行剪裁。

剪裁的过程其实就是将场景中的目的物标记圈出来，一般为矩形窗口框圈出。

矩形窗口框为闪动的虚线框，可以根据剪裁的目的物大小随意变换矩形框的大小。

此外具体说来，剪裁算法还有其他的形式。

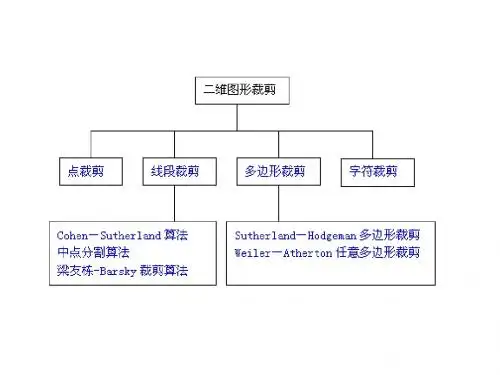
如：点剪裁，线段剪裁，多边形剪裁，曲线及文字剪裁等。

现在笔者再详细介绍二维剪裁算法。

二维剪裁算法分为两种，一种是对线段的剪裁，一种是对多边形的剪裁。

因为线段和多边形往往是二维平面中的图形，故而使用二维剪裁算法对其进行剪裁。

目前对该领域的研究已经取得了很丰硕的成果，已经有很多成熟也高效实用的二维剪裁算法。

详细地来说，这些经典的算法有Cyrus—berk二维剪裁算法，Cohen—Sutherland二维多边形剪裁算法等等。

2 椭圆形窗口线剪裁算法的简介在计算机图形学中，椭圆形窗口线剪裁算法是十分重要的一种基础算法。

该算法之所以十分重要，笔者总结为两点原因：首先椭圆形是几何图形中最基础的图形之一，其次在我们的日常生活和工作当中有很多地方的剪裁工作是更适合椭圆形的（我们生活与工作之中，很少有标准的圆形目的物去剪裁，更多情况下是不规则的图像剪裁，而椭圆形可以更好的，更多的剪裁出合适的目的物）。

计算机图形学实验报告2015-2016学年第一学期班级计自1302 学号姓名一．实验内容与实验步骤1.实验内容实现一个二维或三维裁剪算法，或实现一个Bezier曲线或Bezier曲面算法，并能够实现曲线曲面的形状修改。

2.主要思路每一裁剪窗口边界将二维空间划分成内部和外部的两个半空间。

一旦给所有的的线段端点建立了区域码，就可以快速判断哪条线段完全在裁剪窗口之内，哪条线段完全在窗口之外。

3.部分源代#include"stdafx.h"#include<GL/glut.h>#include<math.h>#include<GL/gl.h>#include<stdio.h>#include<stdlib.h>int flag;void setPixel(GLintx,GLint y){glBegin(GL_POINTS);glVertex2i(x, y);glEnd();}/* Bresenham line-drawing procedure for |m| < 1.0. */void lineBres (float x0, float y0, float xEnd, float yEnd){int dx =fabs(xEnd - x0), dy =fabs(yEnd - y0);int p = 2 * dy - dx;int twoDy = 2 * dy, twoDyMinusDx = 2 * (dy - dx);int x, y;/* Determine which endpoint to use as start position. */if (x0 >xEnd) {x = xEnd;y = yEnd;xEnd = x0;}else {x = x0;y = y0;}setPixel (x, y);while (x <xEnd) {x++;if (p < 0)p += twoDy;else {y++;p += twoDyMinusDx;}setPixel (x, y);}}class wcPt2D {public:GLfloat x, y;};inline GLint round (const GLfloat a) { return GLint (a + 0.5); }/* Define a four-bit code for each of the outside regions of a * rectangular clipping window.*/const GLintwinLeftBitCode = 0x1;const GLintwinRightBitCode = 0x2;const GLintwinBottomBitCode = 0x4;const GLintwinTopBitCode = 0x8;inline GLint inside (GLint code) { return GLint (!code); } inline GLint reject (GLint code1, GLint code2){ return GLint (code1 & code2); }inline GLint accept (GLint code1, GLint code2){ return GLint (!(code1 | code2)); }GLubyte encode (wcPt2D pt, wcPt2D winMin, wcPt2D winMax){GLubyte code = 0x00;if (pt.x<winMin.x)code = code | winLeftBitCode;if (pt.x>winMax.x)code = code | winRightBitCode;if (pt.y<winMin.y)code = code | winBottomBitCode;if (pt.y>winMax.y)code = code | winTopBitCode;return (code);}void swapPts (wcPt2D * p1, wcPt2D * p2){wcPt2Dtmp;tmp = *p1; *p1 = *p2; *p2 = tmp;}void swapCodes (GLubyte * c1, GLubyte * c2){GLubytetmp;tmp = *c1; *c1 = *c2; *c2 = tmp;}void lineClipCohSuth (wcPt2D winMin, wcPt2D winMax, wcPt2D p1, wcPt2D p2) {GLubyte code1, code2;GLint done = false, plotLine = false;GLfloat m;while (!done) {code1 = encode (p1, winMin, winMax);code2 = encode (p2, winMin, winMax);if (accept (code1, code2)) {done = true;plotLine = true;}elseif (reject (code1, code2))done = true;else {/* Label the endpoint outside the display window as p1. */if (inside (code1)) {swapPts (&p1, &p2);swapCodes (&code1, &code2);}/* Use slope m to find line-clipEdge intersection. */if (p2.x != p1.x)m = (p2.y - p1.y) / (p2.x - p1.x);if (code1 &winLeftBitCode) {p1.y += (winMin.x - p1.x) * m;p1.x = winMin.x;}elseif (code1 &winRightBitCode) {p1.y += (winMax.x - p1.x) * m;p1.x = winMax.x;}elseif (code1 &winBottomBitCode) {/* Need to update p1.x for nonvertical lines only. */if (p2.x != p1.x)p1.x += (winMin.y - p1.y) / m;p1.y = winMin.y;}elseif (code1 &winTopBitCode) {if (p2.x != p1.x)p1.x += (winMax.y - p1.y) / m;p1.y = winMax.y;}}}if (plotLine)lineBres (round (p1.x), round (p1.y), round (p2.x), round (p2.y)); void myDisplay(){wcPt2DwinMin , winMax , p1 , p2;winMin.x=100; winMin.y=200;winMax.x=400; winMax.y=400;p1.x=50; p1.y=50;p2.x=450; p2.y=450;glClear(GL_COLOR_BUFFER_BIT);glColor3f (1.0f, 0.0f, 0.0f);glRectf(winMin.x ,winMin.y ,winMax.x,winMax.y);glColor3f (1.0f, 1.0f, 1.0f);if (flag){lineClipCohSuth (winMin, winMax,p1,p2);}else{glBegin(GL_LINES);glVertex2i(p1.x,p1.y);glVertex2i(p2.x,p2.y);glEnd();}glFlush();}void Init(){glClearColor(0.0, 0.0, 0.0, 0.0);glMatrixMode (GL_PROJECTION);gluOrtho2D (0.0, 640.0, 0.0, 480.0);}void Reshape(int w, int h){glViewport(0, 0, (GLsizei) w, (GLsizei) h);glMatrixMode(GL_PROJECTION);glLoadIdentity();gluOrtho2D(0.0, (GLdouble) w, 0.0, (GLdouble) h);}void keyboard(unsignedchar key, int x, int y) {if (key=='c' || key=='C') flag=true;if (key=='r' || key=='R') flag=false;glutPostRedisplay();}int main(int argc, char *argv[]){glutInit(&argc, argv);glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE);glutInitWindowPosition(100, 100);glutInitWindowSize(640, 480);glutCreateWindow("Cohen-Sutherland直线裁减算法，C 键裁减，R键复原"); Init();glutDisplayFunc(myDisplay);glutReshapeFunc(Reshape);glutKeyboardFunc(keyboard);glutMainLoop();return 0;}二．实验结果三．实验总结这次实验我的收获主要有两个方面：一是编程水平的提高，还有一个是对计算机图形学理论知识的巩固。