3' 4'
d' b' 0
D d
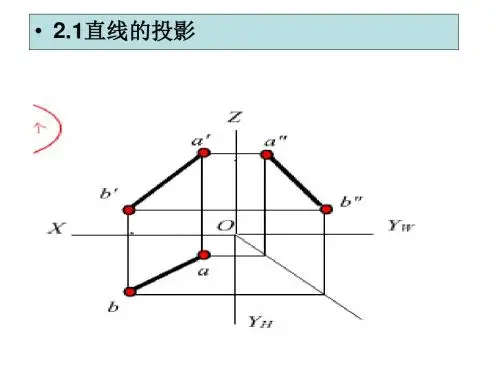
X
2 b a H 1 3(4)
b d
判别方法: 判别方法: 若空间两直线交叉,则其三面投影无共有点, 若空间两直线交叉,则其三面投影无共有点, 至少有一对投影不平行。如图所示, 至少有一对投影不平行。如图所示,三面投影 的相交处是重影点。 的相交处是重影点。
应当强调指出的是: 应当强调指出的是 判断两直线是平行、 判断两直线是平行、相 交或交叉,必须对其三面 交或交叉 必须对其三面 投影进行综合分析否则 容易造成误判,如图所示 容易造成误判 如图所示 的两直线,其 的两直线 其V 、H投影 投影 是平行的,但 投影却显 是平行的 但W投影却显 示出两直线是交叉两直 线. 求出侧面投影可知: 求出侧面投影可知:
a′ ′ c9 9 c
●
投影特性:
d′ ′
1′(2′ ) 3′ ′ ′ ′ 4′ ′
●
为什么? 为什么? 两直线相交吗? 两直线相交吗?
b′ ′
●
●
2
●
b d
a
1 3(4 )
●
Ⅰ、Ⅱ是V面的重影点, 面的重影点, 面的重影点。 Ⅲ、Ⅳ是H面的重影点。 面的重影点
同名投影可能相交, ★ 同名投影可能相交, 交点” 但 “交点”不符合空间 一个点的投影规律。 一个点的投影规律。 交点” ★ “交点”是两直线上 重影点的投影, 的一 对重影点的投影, 用其可帮助判断两直线 的空间位置。 的空间位置。
2.定比性:由初等几何知识可以证明,C点分直线 2.定比性 由初等几何知识可以证明,C点分直线 定比性: AB及其投影成定比. AB及其投影成定比 及其投影成定比. :AC:CB=ac’ :c’ :cb=a’’c c’’b 即:AC:CB=ac’ :c’b’=ac :cb=a’’c’’ : c’’b’’