华师大版初中数学七年级下册机会的均等与不等(二)

数学初一下华东师大版11.2机会的均等与不等教案教学目的1.学会判断游戏的公平与不公平，并学会简单的推理。

2.让学生体会随机事件发生与不发生的机会不总是对半的，进展学生简单的逻辑思维能力。

2.通过体会感受数学思考过程的条理性和数学结论的确定性。

教学重点体验不确定事件发生的可能性有大有小。

教学难点随机观念的形成。

教学过程【一】创设情境假如小明邀请你玩一个抛掷两枚硬币的游戏，游戏规那么如此：抛出两个正面----你赢1分；抛出其他结果----小明赢1分；谁先到10分，谁就得胜。

你会和小明玩那个游戏吗？那个游戏规那么对你和小明公平吗？【二】探究归纳1.一个公平的游戏应该是游戏双方各有50%赢的机会，而上面小明建议玩的那个游戏，由前面我们学过的知识可知，他赢的机会为75%，游戏规那么明显不公平，你所以可不能情愿和他玩啦。

2.下面再给出三个游戏，你认为它们公平吗？游戏1由两个人玩的“抢30”游戏，也许你往常曾经玩过。

那个游戏的规那么是如此的：第一个人先说“1”或“1。

2”，第二个人要接着往下说一个或两个数，然后又轮到第一个人，再接着往下说一个或两个数，如此两人反复轮流，每次每人说一个或两个数都能够，然而不能够连说三个数，谁先抢到30，谁就得胜。

和你的同伴玩一玩那个“抢30”游戏，只是，在游戏开始前，建议你们双方先考虑一下有没有克敌制胜的策略。

游戏开始后，双方报数要快，不同意拖拉。

游戏后小结这是一个偏向第2个报数人的游戏，你发明了吗？在分析获胜策略的时候，我们能够如此来理解：要抢到30，先要抢到27；要抢到27；先要抢到24；要抢到24，先要抢到21，……要抢到6，先要抢到3；要抢到3，只有让对方先开始，显然那个游戏不公平。

游戏2这是一个抛掷两个筹码的游戏。

预备两个筹码，一个两面都画上╳；另一个一面画上╳，另一面画上○。

甲、乙各持一个筹码，抛掷手中的筹码。

游戏规那么：掷出一对╳，甲得1分；掷出一个╳一个○，乙得1分。

§ 10.4机会的均等与不等第一课时：确定与不确定教学内容：§ 10.4机会的均等与不等（1、确定与不确定）教学目标：1、理解确定事件和不确定事件，并理解确定事件与不确定事件的区 别与联系。

能正确判断一些事件属哪类事件，能自己举出例子。

2、 通过对实际生活经验出发，引导学生辨别“必然事件”、“不可 能 事件”、“随机事件”，并弄清它们的区别与联系。

3、 体验思考的快乐，激发学生的学习兴趣。

教学重点：对确定事件与不确定事件的区别与联系， 对事件确定与不确定做出判 断。

教学难点：对确定事件与不确定事件的理解。

教学准备：投影仪，投影片教学方法：讨论式教学过程：一、新课导入我们已经知道，世界上的有些事情即使我们还没有尝试， 我们也能够预先判 断它们必然会发生或者必然不会发生•请把你的判断填入下表提问：请判断上边事件，哪些一定会发生，哪些一定不会发生？为什么？二、新课板书课题：§ 10.4机会的均等与不等 1、确定与不确定问：①④这样的事件称为必然事件，请归纳什么叫必然事件？ 生：无需通过实验就能够预先确定它们在每一次实验中都一定会发生的事件为 必 然事件。

问：②③⑤中一定不会发生称为不可能事件，请归纳什么叫不可能事件？ 生：称那些在每一次实验中都一定不会发生的事件为不可能事件。

师:这两种事件在实验中是否发生都是我们能够预先确定的， 统称为确定的事件。

板书必然事件，不可能事件，确定事件的定义问：必然事件、不可能事件、确定事件这三者之间的关系是怎样的?师：请把刚才表格中填的“会、不会”改为必然事件与不可能事件，要尽量的用 数学术语来回答。

生: 确定事件 :必然事件'不可能事件师：但是，世界上还有大量的事情在还没有尝试之前，我们是无法预先确定它们会不会发生的，例如，如下图所示物体的有关事件：随机转动（1）用力旋转画有红、黄、蓝、绿四色转盘上的指针，指针会停在红色上；师：我们学校门口原来有一种游戏，去拔动转盘上的指针，用力旋转，停的位置是一个什么动物，用糖奖给参与者，是否每次都停在我们想要的位置呢？生：不一定。

2019-2020学年七年级数学下册 10.4 机会的均等与不等2教案 华东师大版教学目标1．经历猜测、试验、分析试验结果等活动。

2．进一步体验不确定事件发生的可能性有大有小。

重点、难点重点：体验不确定事件发生的可能性有大有小。

难点；随机观念的形成。

教学过程一、问题的提出上节课时作业设计中第一大题的第2小题的实验你发现了哪些问题?1．每次摸球的时候，有没有将球摇匀。

2．有没有制定摸球时不要偷看。

3．最后有没有把盒子里的球倒出来检验一下红、黄两个颜色的球是否一样。

如果不一样，机会就不一样。

以上三点都会造成不公平。

鉴于以上的情况，所以彩券的播奖时，选票的计算时，都需要请公证处公证。

请大家阅读120 “搅匀对保证公平很重要”一文，这对学习本节是有启发的。

二、现在我们看下面游戏如果张小春邀请你玩一个抛掷两枚硬币的游戏。

其游戏规则是这样的抛出两个正面——你赢1分，抛出其他结果——张小明赢1分；谁先到10分，谁就胜。

试问你会跟张小明玩这个游戏吗?这个游戏对你、对张小明公平吗?从上面试验发现：得到两个正面的成功率只有0.25，也就是说只有14的机会，而得不到两个正面的成功率就有0.75即就有34的机会， 所以你就不会与张小明玩这个游戏。

要想这个游戏玩得公平，你准备如何修改游戏规则才会使大家机会均等。

所谓机会均等就是游戏双方各有50％赢的机会。

三、由两个人玩“抡30”游戏，这个游戏规则是这样的第一个人先说“1”或“1、2”，第2个人接着往下说一个或二个数，然后又轮到第一个人再接着往下说一个或二个数，这样两人反复轮流，每次每人说一个或两个都可以，但不可不说或连说三个或三个以上的数，谁先抢到30，谁就得胜。

我们先想一下这个游戏公平吗?表面上看似乎这个游戏很公平，如果你能认真地考虑就感到不公平了，为什么? 游戏开始后，双方报数要快，不允许拖拉。

大家通过认真思索就不难发现，要抢到30，必要抢到27，要抢到 27，必要抢到24，要抢到24，必要抢到21，要抢到21，必要抢到18，要抢到18，必要抢到15……先要抢到3。

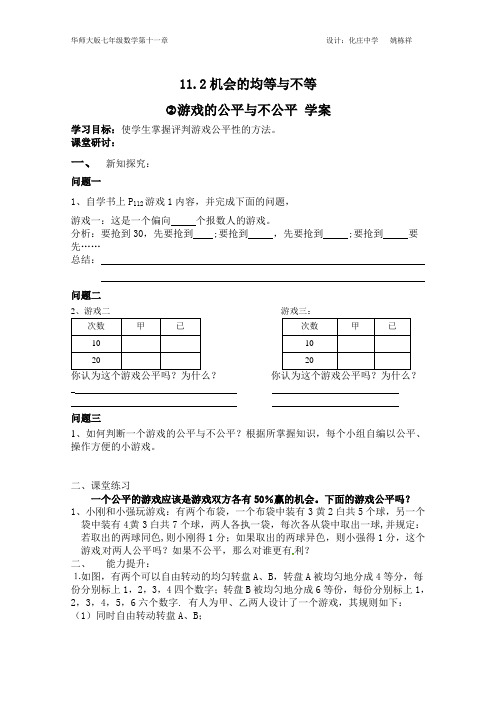
11.2机会的均等与不等游戏的公平与不公平学案学习目标：使学生掌握评判游戏公平性的方法。

课堂研讨：一、新知探究：问题一1、自学书上P112游戏1内容，并完成下面的问题，游戏一：这是一个偏向个报数人的游戏。

分析：要抢到30，先要抢到 ;要抢到，先要抢到 ;要抢到要先……总结：问题二2、游戏二游戏三：次数甲已次数甲已10 1020 20你认为这个游戏公平吗？为什么？你认为这个游戏公平吗？为什么？问题三1、如何判断一个游戏的公平与不公平？根据所掌握知识，每个小组自编以公平、操作方便的小游戏。

二、课堂练习一个公平的游戏应该是游戏双方各有50％赢的机会。

下面的游戏公平吗？1、小刚和小强玩游戏：有两个布袋，一个布袋中装有3黄2白共5个球，另一个袋中装有4黄3白共7个球，两人各执一袋，每次各从袋中取出一球,并规定：若取出的两球同色,则小刚得1分；如果取出的两球异色，则小强得1分，这个游戏对两人公平吗？如果不公平，那么对谁更有利？二、能力提升：⒈如图，有两个可以自由转动的均匀转盘A、B，转盘A被均匀地分成4等分，每份分别标上1，2，3，4四个数字；转盘B被均匀地分成6等份，每份分别标上1，2，3，4，5，6六个数字. 有人为甲、乙两人设计了一个游戏，其规则如下：（1）同时自由转动转盘A、B；（2）转盘停止后，指针各指向一个数字（如果指针恰好指在分格线上，那么重转一次，直到指针指向某一数字为止），用所指的两个数字作成积. 如果得到的积是偶数，那么甲胜；如果得到的积是奇数，则乙胜（如果转盘A 指针指向3，转盘B 指针指向5，3×5=15，按规则乙胜）。

你认为这样的规则是否公平？请说明理由；如果不公平，请你设计一个公平的规则，并说明理由。

⒉小莉的爸爸买了今年七月份去上海看世博会的一张门票，她和哥哥两人都很想去观看，可门票只有一张，读九年级的哥哥想了一个办法，拿了八张扑克牌，将数字为1，2，3，5的四张牌给小莉，将数字为4，6，7，8的四张牌留给自己，并按如下游戏规则进行：小莉和哥哥从各自的四张牌中随机抽出一张，然后将抽出的两张扑克牌数字相加，如果和为偶数，则小莉去；如果和为奇数，则哥哥去． （1）请用数状图或列表的方法，求小莉去上海看世博会的概率；（2）哥哥设计的游戏规则公平吗？若公平，请说明理由；若不公平，请你设计一种公平的游戏规则。

§10.4机会的均等与不等第二课时：成功与失败教学内容：§10.4机会的均等与不等(2、成功与失败)教学目标：1、知识与技能目标：理解随机事件在每一次试验中是否发生是不可预言的。

但在大次数的反复试验中，随机事件发生的频率（成功率）会逐渐稳定在某一数值上。

在大量的随机事件中存在着必然的规律，通过实验设法预测随机事件每次实验中发生的可能性；知道大量重复试验时，频率可作为事件发生概率的估计值。

2、过程与方法目标：通过抛掷硬币实验，引导学生理解大次数的反复试验中，随机事件发生的频率（成功率）会逐渐稳定在某一数值上，这个数值称为频率。

3、情感与态度目标：让学生获得一些研究问题的方法和经验，发展思维能力，体验思考的快乐，激发学生的学习兴趣。

教学重点：继续加深理解随机事件在每一次试验中是否发生是不可预言的；理解实验成功率随实验次数增加而逐渐趋于稳定。

教学难点：（1）结果的随机性，即在相同的条件下做重复试验时，如果试验的结果不止一个，那么在试验前无法预料哪一种结果将发生。

（2）频率的稳定性，即大量重复试验时，任意结果（事件）A的出现的频率尽管是随机的，却“稳定”在某一个常数附近，试验的次数越多，频率与这一常数的偏差大的可能性越小，这一常数就成为该事件的概率。

（3）纠正学生的错误观点：既然随机事件在一次实验中可能发生也可能不发生，所以它发生和不发生的机会各占一半，都为50%。

这是一种较为常见的概念错误。

教学准备：多媒体课件、硬币若干教学方法：活动、讨论、归纳总结教学过程：一、新课导入在一次实验中，不确定事件是否会发生是无法预料的，如果发生了，我们就说它在这次实验中成功了；反之，我们就说它在这次实验中失败了。

今天这节课我们要讨论的就是事件的成功与失败的规律。

（师板书：§10.4机会的均等与不等2、成功与失败）二、新课1．大家肯定玩过抛掷硬币的游戏，现在各位同学与你的同伴合作，做一做抛掷两枚硬币的游戏，每人各抛10次，一位同学抛的时候，另一位同学帮着记录实验结果。

第2节机会的均等与不等要点精讲1、确定与不确定（1）必然事件：无需通过实验就能预先确定它们在每一次实验中都会发生的事件叫必然事件。

如：①从一个只装有红球的盒子里摸出一个红球；②人总有一天会死去。

都是必然事件。

（2）不可能事件：在每一次实验中都一定不会发生的事件叫不可能事件。

如：①人可以不喝水；②投一枚骰子（点数为1—6）投出7点。

都是不可能事件。

必然事件与不可能事件称为确定事件，即：（3）不确定事件：无法预先确定在一次实验中会不会发生的事件叫不确定事件，或随机事件。

如：①用手抓一把小米，数一下刚好有 5000粒；②到街上买一注“足彩”号就中了大奖；③开车在交通繁忙的主干道上闯红灯竟然没有出现交通事故。

（4）确定事件的发生率为100%，不可能事件的发生率为0，而随机事件的发生率大于0，小于100%.2、成功与失败在一次实验中，不确定事件是否会发生，我们无法预料.如果发生了，则说它在这次实验中成功了.反之，则说它在这次实验中失败了.叫成功率，一般用百分数（或小数）表示.叫失败率，一般也用百分数（或小数）表示.事件发生的次数和发生率（）也叫频率，随机事件的发生率虽然是不可预言的，但是大量实验后的事件发生的频率就比较稳定了（实验次数过少，偶然性很大，频率值波动就大）.3、游戏的公平与不公平——机会的均等与不均等.当一个游戏的规则使双方赢的机会相同时，这个游戏就是公平的游戏，如果使一方的赢的机会超过另一方时，这个游戏就是不公平的 .如：小明和小华为了争当班级足球队的守门员，设计了一个抛掷两枚硬币的游戏.规定是这样的：抛出两个正面——小明得1分；抛出一反一正——小华得1分.谁先积满10分谁就去当守门员.你觉得这个游戏规则公平吗？谁获胜当守门员的可能性更大？对于两枚硬币，抛掷出“一反一正”的机会一般是50%，大于抛掷出“两个正面”的机会25%，因为机会不均等，亦既游戏规则不公平，当然是小华获胜当守门员的可能性大. 如将规则改为：抛出两个正面——小明得2分；抛出一反一正——小华得1分.则这个游戏是公平的。