【精准解析】湖南省长沙市长郡中学2020届高三下学期二月网络教学质量监测卷理综物理试题

绝密★启用前2020届湘赣皖·长郡十五校高三联考 第二次考试理科综合能力测试由 联合命题时量：150分钟 总分：300分注意事项：1．本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2．回答第Ⅰ卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动用橡皮擦干净后，再选涂其他答案标号。

写在本试卷上无效。

3．回答第Ⅱ卷时，将答案写在答题卡上。

写在本试卷上无效。

4．考试结束后．将本试卷和答题卡一并交回。

可能用到的相对原子质量：H~1 T~3 C~12 N~14 O~16 Na~23 P~31 Fe~56 Cu~64 Ce~140 第I 卷(选择题，共126分)一、选择题：本题共13小题，每小题6分，共78分。

每小题给出的四个选项中，只有一项是符合题目要求的。

1．下列有关细胞结构和功能的叙述正确的是A ．细胞之间的信息交流不一定都要通过细胞膜上的糖蛋白来实现B ．当细胞内外存在浓度差时，细胞就会发生质壁分离或质壁分离复原C ．盐析和高温都能使蛋白质分子的空间结构变得伸展、松散，易被蛋白酶水解D ．吞噬细胞中的溶酶体能合成和储存大量的水解酶，可以水解衰老的细胞器和病原体2．中耕松土是农作物栽培过程中经常使用的一项措施，结合所学的生物学知识进行分析判断，下列说法不合理的是A ．松土可促进根的细胞呼吸，促进农作物对矿质离子的主动吸收B ．现代农业生产应当提倡免耕法，大力推广比较环保的无土栽培技术C ．松土易造成水土流失，可能成为沙尘暴的一种诱发因素D ．松土可促进土壤中微生物对腐殖质的分解，加速物质和能量的循环利用3．我国科学家研究发现水稻细胞核中的Ghd7基因编码的蛋白质不仅参与了开花的调节，而且对水稻的生长、发育和产量都有重要影响。

根据此项研究结果可以得出的结论是A ．Chd7基因的表达是边转录边翻译形成多肽，多肽还要轻内质网和高尔基体的加工B ．基因可以通过控制酶的合成来控制代谢，从而控制生物的有关性状C ．该项研究表明生物的性状与基因的关系并不是简单的一一对应关系D ．水稻植物的开花只受细胞核中Ghd7基因的控制长郡中学；街阳八中；永州市四中；岳阳县一中；湘潭县一中；湘西州民中；九江市一中；石门一中；澧县一中；益阳市一中；桃源县一中；株洲市二中；麓山国际；南昌二中；合肥八中4．下图是某家族中某种人类遗传病的系谱图，据图分析判断，下列说法正确的是A．该遗传病是伴X染色体隐性遗传病，男性患者的后代中，女性一定是携带者B．若Ⅳ—1号个体是携带者的几率为1/4，则该遗传病可能为红绿色盲病C．若该遗传病为白化病，则Ⅲ—3号个体的致病基因不可能来自Ⅰ—1号个体D．若Ⅲ—3号个体的性染色体组成为XYY，则可能是Ⅱ—1号个体在减数第一次分裂时出现了异常5．马拉松长跑是赛程超过40 km、历时2 h以上的极限运动，在运动过程中，运动员会呼吸加快，大量流汗，每小时至少要消耗300 g糖类，但运动员体内血糖的含量仍然稳定在0.9g/L左右。

湖南省长郡中学2020届高三月考试题（二）物理试卷一、单项选择题：本题共6小题，每小题4分，共24分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、吴菊萍徒手勇救小妞妞，被誉为“最美妈妈”。

若两岁的妞妞质量约为12kg，从十楼坠落，下落高度为28.8m，吴菊萍的手臂与妞妞的接触时间约为0.1s，已知重力加速度g=10m/s2，则她受到的冲击力约为A．3000N B．2880N C．1440N D．3220N2、下列说法符合物理学史实的是（）A．亚里士多德最早指出力不是维持物体运动的原因B．库仑在前人研究的基础上，通过扭秤实验研究得出了库仑定律C．卡文迪许提出了万有引力定律，并通过实验测出了万有引力常量D．哥白尼提出了日心说并发现了行星沿椭圆轨道运行的规律3、下列现象中属于分子斥力的宏观表现的是A．镜子破碎后再对接无法接起B．液体体积很难压缩C．打气筒打气，若干次后难再打进D．橡皮筋拉伸后放开会自动缩回4、放置于固定斜面上的物块，在平行于斜面向上的拉力F作用下，沿斜面向上做直线运动。

拉力F和物块速度v随时间t变化的图象如图，则不正确的是：（）A．第1s内物块受到的合外力为0.5NB．物块的质量为11kgC．第1s内拉力F的功率逐渐增大D．前3s内物块机械能一直增大5、如图所示，是一个质点在时间内的v-t图象，在这段时间内，质点沿正方向运动的平均速度大小为v1沿负方向运动的平均速度大小为v2则下列判断正确的是( )A．v1>v2B．v1<v2C．v1=v2D．以上三种情况均有可能6、2019年诺贝尔物理学奖授予了三位天文学家，以表彰他们对于人类对宇宙演化方面的了解所作的贡献。

其中两位学者的贡献是首次发现地外行星，其主要原理是恒星和其行星在引力作用下构成一个“双星系统”，恒星在周期性运动时，可通过观察其光谱的周期性变化知道其运动周期，从而证实其附近存在行星。

若观测到的某恒星运动周期为T，并测得该恒星与行星的距离为L，已知万有引力常量为G，则由这些物理量可以求得（）A．行星的质量B．恒星的质量C．恒星与行星的质量之和D．恒星与行星圆周运动的半径之比二、多项选择题：本题共4小题，每小题5分，共20分。

长郡中学2020届高三适应性考试（二）数学（理科）试卷本试题卷共8页，共23题（含选考题）.全卷满分150分.考试建议用时120分钟.注意事项：1.答题前，考生可能需要输入信息.请务必正确输入所需的信息，如姓名、考生号等.2.选择题的作答：请直接在选择题页面内作答并提交.写在试题卷、草稿纸等非答题区域均无效.3.非选择题的作答：用签字笔直接答在答题卡，上对应的答题区域内或空白纸张上，按规定上传.4.选考题的作答：先把所选题目的题号在答题卡，上指定的位置用笔涂黑，或者在空白纸张上注明所写题目，然后开始作答.一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有-项是符合题目要求的.1.已知集合{|}A x Z x a =∈≥，集合{4}xB x =∈Z |2≤，若A B I 只有4个子集，则a 的取值范围是（ ）A .(2,1]--B .[2,1]--C .[0,1]D .(0,1]2.已知复数1(1)3z i i +=-，复数22(1)z i i =-，给出下列命题： ①12z z >；②12||||z z >；③复数1z 与其共轭复数在复平面内的点关于实轴对称；④复数2z 的虚部为0. 其中真命题的个数为（ ）A .1B .2C .3D .43.已知某一组散点数据对应的线性回归方程为ˆˆ0.76yx a =-+，数据中心点为(5,1)，则7.5x =的预报值是（ ）A .0.9B .0.9-C .1D .1-4.斐波那契数列（Fibonacci sequence ）又称黄金分割数列，因数学家列昂纳多•斐波那契（ Leonardoda Fibonacci ）以兔子繁殖为例子而引入，故又称为“兔子数列”.在数学上，斐波纳契数列被以下递推的方法定义：数列{}n a 满足：121a a ==，21 n n n a a a ++=+，现从数列的前2024项中随机抽取1项，能被3整除的概率是（ ）A .14B .13C .23D .125.已知5(1)x的展开式的常数项为a ，则1181(21)a x dx --=⎰（ ）A .5B .6C .7D .96.已知0a b >>，1ab =，设2a b x =，2log ()y a b =+，1z a b=+，则log 2x x ，log 2y y ，log 2z z 的大小关系为（ ）A .log 2log 2log 2x y z x y z >>B .log 2log 2log 2y z x y z x >>C .log 2log 2log 2x z y x z y >>D .log 2log 2log 2y x z y x z >>7.某几何体的三视图如图所示，则该几何体中，最长的棱的长度为（ ）A .B .C .3 D8.将函数()cos f x x =的图象先向右平移56π个单位长度，在把所得函数图象的横坐标变为原来的1ω(0)ω>倍，纵坐标不变，得到函数()g x 的图象，若函数()g x 3(,)22ππ上没有零点，则ω的取值范围是（ ）A .228(0,][,]939UB .2(0,]9C . 28(0,][,1]99UD .(0,1] 9.已知12,F F 分别为椭圆221168x y +=的左、右焦点，M 是椭圆上一点，过点2F 作12F MF ∠的角平分线的垂线，垂足为N ，若||2ON =（O 为坐标原点），则||OM =（ ）A B C D .10.已知三棱柱111ABC A B C -四边形11A ACC 与11B BCC 均为正方形，,M N 分别是11A B ，11A C 的中点，11112C M A B =，则异面直线BM 与AN 所成角的余弦值为（ ）A .310 B.10 C .710D.10 11.函数2()(3)x f x x e =-，关于x 的方程2()()10f x mf x -+=恰有四个不同实数根，则实数m 的取值范围为（ ）A .(0,2)B .(2,)+∞C .336(0,)6e e +D .336(,)6e e ++∞ 12.已知函数()ln(f x x =满足对于任意11[,2]2x ∈，存在21[,2]2x ∈，使得22112ln (2)()x f x x a f x ++≤成立，则实数a 的取值范围为（ ） A .ln 2[8,)2-+∞ B .ln 25[8,2ln 2]24--- C .ln 2(,8]2-∞- D .5(,2ln 2]4-∞-- 二、填空题：本大题共4小题，每小题5分，共20分.13.已知向量(1,sin 1)AC α=-u u u r ，(3,1)BA =u u u r ，(2,cos )BD α=u u u r ，若,,B C D 三点共线，则tan(2019)πα-= .14.已知实数,x y 满足约束条件212(2)y x y y x ≤⎧⎪+≥⎨⎪≥-⎩，若(0)z x ty t =+>的最大值为11，则实数t = .15.若存在m ，使得()f x m ≥对任意x D ∈恒成立，则函数()f x 在D 上有下界，其中m 为函数()f x 的一个下界；若存在M ，使得()f x M ≤对任意x D ∈恒成立，则函数()f x 在D 上有上界，其中M 为函数()f x 的一个上界.如果一个函数既有上界又有下界，那么称该函数有界.下列四个结论：①1不是函数()()10f x x x x=+>的一个下界；②函数()ln f x x x =有下界，无上界； ③函数()2x e f x x =号有上界，无下界；④函数2sin ()1x f x x =+有界. 其中所有正确结论的编号为 .16.圆锥Ω的底面半径为2，其侧面展开图是圆心角为180︒的扇形.圆锥的内接正四棱柱（底面为正方形的直棱柱） ABCD A B C D -''''的上底面的顶点', ',', 'A B C D 均在圆锥Ω的侧面上，棱柱下底面在圆锥Ω的底面上，则此正四棱柱体积的最大值为 .。

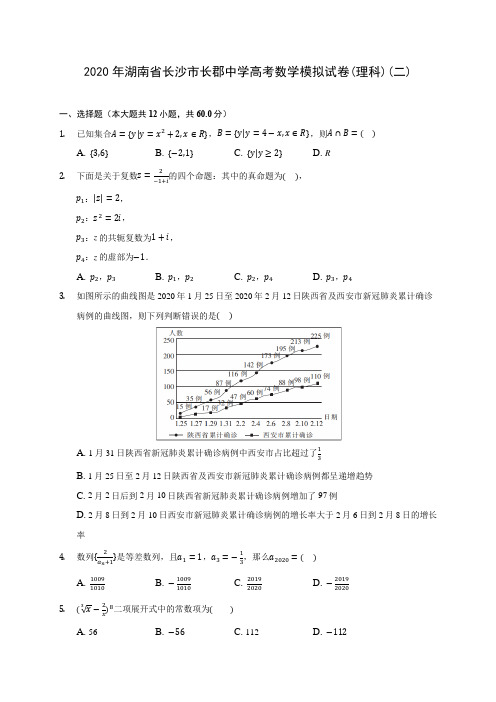
2020年湖南省长沙市长郡中学高考数学模拟试卷(理科)(二)一、选择题（本大题共12小题，共60.0分）1. 已知集合A ={y|y =x 2+2,x ∈R}，B ={y|y =4−x,x ∈R}，则A ∩B =( )A. {3,6}B. {−2,1}C. {y|y ≥2}D. R2. 下面是关于复数z =2−1+i 的四个命题：其中的真命题为( )，p 1：|z|=2， p 2：z 2=2i ，p 3：z 的共轭复数为1+i ， p 4：z 的虚部为−1．A. p 2，p 3B. p 1，p 2C. p 2，p 4D. p 3，p 43. 如图所示的曲线图是2020年1月25日至2020年2月12日陕西省及西安市新冠肺炎累计确诊病例的曲线图，则下列判断错误的是( )A. 1月31日陕西省新冠肺炎累计确诊病例中西安市占比超过了13B. 1月25日至2月12日陕西省及西安市新冠肺炎累计确诊病例都呈递增趋势C. 2月2日后到2月10日陕西省新冠肺炎累计确诊病例增加了97例D. 2月8日到2月10日西安市新冠肺炎累计确诊病例的增长率大于2月6日到2月8日的增长率 4. 数列{2an+1}是等差数列，且a 1=1，a 3=−13，那么a 2020=( ) A. 10091010B. −10091010C. 20192020D. −201920205. (√x 3−2x )8二项展开式中的常数项为( )A. 56B. −56C. 112D. −1126. 已知a =(12)0.3,b =log 120.3,c =a b，则a ，b ，c 的大小关系是( )A. a <b <cB. c <a <bC. a <c <bD. b <c <a7. 已知，则sin2α=( )A. 12B. √32C. −12D. −√328. 2019年4月25日−27日，北京召开第二届“一带一路”国际高峰论坛，组委会要从6个国内媒体团和3个国外媒体团中选出3个媒体团进行提问，要求这三个媒体团中既有国内媒体团又有国外媒体团，且国内媒体团不能连续提问，则不同的提问方式的种数为( )A. 198B. 268C. 306D. 3789. 在不等式组{x +y −2⩾0,x −y −2⩽0,y ⩽2,，所确定的三角形域内随机取一点，则该点到此三角形的三个顶点的距离均大于1的概率是( )A. π8B. 4−π2C. 1−π8D. 1−π410. 已知圆x 2+y 2=r 2(r >0)与抛物线y 2=2x 交于A,B 两点，与抛物线的准线交于C,D 两点，若四边形ABCD 是矩形，则r 等于( )A. √22B. √2C. √52D. √511. 已知长方体ABCD −A 1B 1C 1D 1中，AB =AD =2，AA 1=4，M 是BB 1的中点，点P 在长方体内部或表面上，且平面AB 1D 1，则动点P 的轨迹所形成的区域面积是( )A. 6B. 4√2C. 4√6D. 912. 已知圆C 1：x 2+2cx +y 2=0，圆C 2：x 2−2cx +y 2=0，椭圆C ：x 2a +y 2b=1(a >b >0)，若圆C 1，C 2都在椭圆内，则椭圆离心率的取值范围是( )A. [12,1)B. (0,12]C. [√22,1) D. (0,√22] 二、填空题（本大题共4小题，共20.0分）13. 设函数f(x)在(0,+∞)内可导，且f(e x )=x +e x ，则f′(1)=________． 14. 已知|a ⃗ |=1，b ⃗ =(1,√3)，(b ⃗ −a ⃗ )⊥a ⃗ ，则向量a ⃗ 与向量b ⃗ 的夹角为______．15. 甲罐中有5个红球，2个白球和3个黑球，乙罐中有4个红球，3个白球和3个黑球.先从甲罐中随机取出1个球放入乙罐，分别以A 1，A 2和A 3表示事件从甲罐取出的球是红球，白球和黑球;再从乙罐中随机取出1个球，以B表示事件从乙罐取出的球是红球.则下列结论中正确的是(写出所有正确结论的编号)． ①P(B)=25; ②P(B|A1)=511; ③事件B与事件A1相互独立; ④A1，A2，A3是两两互斥的事件．16.已知数列{a n}满足a1=0，a n+1=a n+n，则a2013=______ ．三、解答题（本大题共7小题，共82.0分）17.在△ABC中，内角A，B，C的所对边分别为a，b，c.已知a2+b2+5abcosC=0，sin2C=72sinAsinB．(Ⅰ)求角C的大小；(Ⅱ)若a=1，求△ABC面积．18.如图，四棱锥P−ABCD中，底面ABCD是平行四边形，∠BAD=60°，∠PAD=45°，点E在线段AB上，PE⊥AD且AB=3，AD=PE=AE=2．(1)求证：平面PAD⊥平面ABCD．(2)求直线PA与平面PDE所成角的正弦值．19.设椭圆x2a +y2b=1(a>b>0)的左焦点为F，右顶点为A，离心率为12，已知A是抛物线y2=2px(p>0)的焦点，F到抛物线的准线l的距离为12．(Ⅰ)求椭圆的方程和抛物线的方程；(Ⅱ)设l上两点P，Q关于x轴对称，直线AP与椭圆相交于点B(B异于点A)，直线BQ与x轴相交于点D.若△APD的面积为√62，求直线AP的方程．20.已知函数f(x)=m(x2−1)x−2lnx．(1)讨论函数f(x)的单调性；(2)若m=12，证明f(x)有且只有三个零点．21. [某商场以分期付款方式销售某种商品，根据以往资料統计，顾客购买该商品选择分期付款的期数ξ的分布列为其中0<a <1，0<b <1(1)求购买该商品的3位顾客中，恰有2位选择分2期付款的概率；(2)商场销售一件该商品，若顾客选择分2期付款，则商场获得的利润为200元；若顾客选择分3期付款，则商场获得的利润为250元；若顾客选择分4期付款，则商场获得的利润为300元．商场销售两件该商品所获得的利润记为X(单位：元) ①求X 的分布列；②若P(X ≤500)≥0.8，求X 的数学期望EX 的最大值．22. 在直角坐标系xOy 中，直线l 的参数方程为{x =−1−√22ty =2+√22t，(t 为参数)，以坐标原点为极点x 轴的正半轴为极轴建立极坐标系，已知曲线C 的极坐标方程为ρcos 2θ=sinθ． (1)求直线l 的普通方程及曲线C 的直角坐标方程；(2)若直线l 与曲线C 交于A ，B 两点，P(−1,2)，求|PA|⋅|PB|．23.已知函数f(x)=|x+1|．(I)求不等式f(x)<|2x+1|−1的解集M；(Ⅱ)设a，b∈M，证明：f(ab)>f(a)−f(−b)．-------- 答案与解析 --------1.答案：C解析：根据集合的基本运算即可．本题主要考查集合的基本运算，比较基础．解：A={y|y=x2+2,x∈R}={y|y≥2}，B={y|y=4−x,x∈R}=R，则A∩B={y|y≥2}，故选：C2.答案：C解析：解：∵z=2−1+i =2(−1−i)(−1+i)(−1−i)=−1−i，∴p1：|z|=√2，p2：z2=2i，p3：z的共轭复数为−1+i，p4：z的虚部为−1，故选：C．由z=2−1+i =2(−1−i)(−1+i)(−1−i)=−1−i，知p1：|z|=√2，p2：z2=2i，p3：z的共轭复数为−1+i，p4：z的虚部为−1，由此能求出结果．本题考查复数的基本概念，是基础题．解题时要认真审题，仔细解答．3.答案：D解析：解析：本题主要考查学生的数据分析能力和图形阅读理解能力，属于基础题．根据图表中包含的信息对照选项分析即可判断真假．解：对于A，1月31日陕西省新冠肺炎累计确诊病例共有87例，其中西安32例．所以西安所占比例为3287>13，故A 正确，对于B ，由曲线图可知.1月25日至2月12日陕西省及西安市新冠肺炎累计确诊病例都呈递增趋势，故B 正确，对于C ，2月2日后到2月10日陕西省新冠肺炎累计确诊病例增加了213−116−97例，故C 正确， 对于D ，2月8日到2月10日西安新冠肺炎累计确诊病例增加了98−8888=544，2月6日到2月8日西安新冠肺炎累计确诊病例增加了88−7474=737，显然737>544，故D 错误．故选：D ．4.答案：B解析：解：设等差数列{2a n+1}的公差为d ，且a 1=1，a 3=−13，∴2a 1+1=1，2a 3+1=3，∴3=1+2d ，解得d =1． ∴2a n +1=1+n −1=n ，∴a n =2n−1．那么a 2020=22020−1=−10091010． 故选：B ． 设等差数列{2an+1}的公差为d ，且a 1=1，a 3=−13，可得2a 1+1=1，2a 3+1=3，3=1+2d ，解得d.可得通项公式，进而得出结论．本题考查了等差数列的通项公式，考查了推理能力与计算能力，属于基础题．5.答案：C解析：本题主要考查二项式定理的应用，二项展开式的通项公式，求展开式中某项的系数，二项式系数的性质，属于基础题．在二项展开式的通项公式中，令x 的幂指数等于0，求出r 的值，即可求得常数项． 解：(√x 3−2x )8二项展开式的通项公式为T r+1=C 8r⋅x8−r3⋅(−2)r ⋅x −r =(−2)r ⋅C 8r⋅x8−4r3，令8−4r 3=0，求得r =2，可得展开式的常数项为4C 82=112，故选C ．6.答案：B解析：解：b =log 120.3>log 1212=1>a =(12)0.3，c =a b <a ．∴c <a <b ． 故选：B ．利用指数函数与对数函数的单调性即可得出．本题考查了指数函数与对数函数的单调性，考查了推理能力与计算能力，属于基础题．7.答案：A解析：本题考查二倍角公式以及诱导公式，属于基础题． 由，得，再运用二倍角公式以及诱导公式计算，即可得到答案．解：由，得，=−[1−2sin 2(π4+α)]=−(1−2×34)=12． 故选A ．8.答案：A解析：由排列组合及计数问题分类讨论：①若选两个国内媒体一个国外媒体，②若选两个外国媒体一个国内媒体，可得解．本题考查了排列组合及计数问题，属中档题．。

2020长郡中学高中毕业班二月份网络教学质量监测卷理科综合物理部分说明: 1.全卷满分300分,考试时间150分钟。

2.全卷分为试题卷和答题卡,答案要求写在答题卡上,不得在试题卷上作答,否则不给分。

第Ⅰ卷(选择题共126分)可能用到的相对原子质量：H 1 C 12 N 14 O 16 S 32 Cl 35.5 K 39 Ti 48 Fe 56 I 127 Ag-108二、选择题:本大题共8小题,每小题6分。

在每小题给出的四个选项中,第14-17题只有一项符合题目要求,第18-21题有多项符合题目要求。

全部选对的得6分,选对但不全的得3分,有选错的得0分。

14.如图所示，A 、B 两物体的质量分别为A m 、B m ，且A B m m ，整个系统处于静止状态，滑轮的质量和一切摩擦均不计，如果绳一端由Q 点缓慢地向左移到P 点，整个系统重新平衡后，绳的拉力F 和两滑轮间绳与水平方向的夹角θ变化情况是( )A ．F 变大，θ角变大B ．F 变小，θ角变小C ．F 不变，θ角变小D ．F 不变，θ角不变D15.如图所示，AB 杆以恒定角速度ω绕A 点转动，并带动套在光滑水平杆OC 上的质量为M 的小环运动，运动开始时，AB 杆在竖直位置，则小环M 的速度将( )A．逐渐增大B．先减小后增大C．先增大后减小D．逐渐减小16.一滑块在水平地面上沿直线滑行，t＝0时速率为1 m/s.从此刻开始在与速度平行的方向上对其施加一水平作用力F，力F和滑块的速度v随时间的变化规律分别如图甲、乙所示，则(两图取同一正方向，重力加速度g＝10 m/s2)( )A．滑块的质量为0.5 kgB．滑块与水平地面间的动摩擦因数为0.5C．第1 s内摩擦力对滑块做功为－1 JD．第2 s内力F的平均功率为1.5 W17.为估算池中睡莲叶面承受雨滴撞击产生的平均压强，小明在雨天将一圆柱形水杯置于露台，测得1小时内杯中水位上升了45 mm.查询得知，当时雨滴竖直下落速度约为12 m/s，据此估算该压强约为(设雨滴撞击睡莲后无反弹，不计雨滴重力，雨水的密度为1×103 kg/m3)( )A．0.15 Pa B．0.54 PaC．1.5 Pa D．5.4 Pa18.如图所示，光滑绝缘的水平面上有一带电荷量为－q 的点电荷，在距水平面高h 处的空间内存在一场源点电荷＋Q ，两电荷连线与水平面间的夹角θ＝30°，现给－q 一水平初速度，使其恰好能在水平面上做匀速圆周运动(恰好不受支持力)，已知重力加速度为g ，静电力常量为k ，则( )A ．点电荷－q 做匀速圆周运动的向心力为3kQq4h 2B ．点电荷－q 做匀速圆周运动的向心力为3kQq8h 2C ．点电荷－q 做匀速圆周运动的线速度为3ghD ．点电荷－q 做匀速圆周运动的线速度为3gh219.如图甲所示，两水平金属板间距为d ，板间电场强度的变化规律如图乙所示．t ＝0时刻，质量为m 的带电微粒以初速度v 0沿中线射入两板间，0～T3时间内微粒匀速运动，T 时刻微粒恰好经金属板边缘飞出．微粒运动过程中未与金属板接触．重力加速度的大小为g .关于微粒在0～T 时间内运动的描述，正确的是( )A ．末速度大小为2v 0B ．末速度沿水平方向C ．重力势能减少了12mgdD ．克服电场力做功为mgd20.如图所示为一种质谱仪的示意图，由加速电场、静电分析器和磁分析器组成．若静电分析器通道中心线的半径为R ，通道内均匀辐射电场，在中心线处的电场强度大小为E ，磁分析器有范围足够大的有界匀强磁场，磁感应强度大小为B 、方向垂直于纸面向外．一质量为m 、电荷量为q 的粒子从静止开始经加速电场加速后沿中心线通过静电分析器，由P 点垂直边界进入磁分析器，最终打到胶片上的Q 点．不计粒子重力．下列说法正确的是( )A ．极板M 比极板N 的电势高B ．加速电场的电压U ＝ERC ．直径PQ ＝2B qmERD ．若一群粒子从静止开始经过题述过程都落在胶片上的同一点，则该群粒子具有相同的比荷21.如图所示，矩形线框abcd 处于磁感应强度为B 的匀强磁场中，磁场方向与线框平面垂直，线框ab 长为2L ，bc 长为L ，MN 为垂直于ab 并可在ab 和cd 上自由滑动的金属杆，且杆与ab 和cd 接触良好，abcd 和MN 上单位长度的电阻皆为r .让MN 从ad 处开始以速度v 向右匀速滑动，设MN 与ad 之间的距离为x (0≤x ≤2L )，则在整个过程中( )A.当x ＝0时，MN 中电流最小B.当x ＝L 时，MN 中电流最小C.MN 中电流的最小值为2Bv5rD.MN 中电流的最大值为6Bv11r三、非选择题:包括必考题和选考题两部分。

物理试题共4页。

满分110分.时间90分钟。

注意事项：1.答题前，务必将自己的姓名、准考证号填写在答题卡规定的位置上。

2.答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案标号。

3.答非选择题时，必须使用0.5毫米黑色签字笔，将答案书写在答题卡规定的位置上。

4.所有题目必须在答题卡上作答，在试题卷上答题无效。

一、选择题(本题共12小题，总48分，每小题4分，其中1-8题为单项选择题，9-12题为多项选择题，选对不选全得2分，错选得0分)1.根据热力学定律和分子动理论，可知下列说法正确的是（）A.不管科技如何进步，绝对零度都不能达到B.为了增加物体的内能，必须给物体传递热量C.空气压缩到一定程度很难再压缩是因为分子间存在斥力的作用D.可以利用高科技手段，将散失到环境中的内能重新收集起来加以利用而不引起其他变化2.物理学家做了一个有趣的实验：在光屏处放上照相用的底片.若减弱光的强度，使光子只能一个一个地通过狭缝.实验结果表明，如果曝光时间不太长，底片只能出现一些不规则的点子；如果曝光时间足够长，底片上就会出现规则的干涉条纹，对这个实验结果有下列认识，其中正确的是（）A.曝光时间不长时，底片上只能出现不规则的点子，表现出光的波动性B.单个光子通过双缝后的落点可以预测C.只有大量光子的行为才能表现出光的粒子性D.干涉条纹中明亮的部分是光子到达机会较多的地方3.一定质量的理想气体的状态变化过程如题3图所示，MN为一条直线，则气体从状态M到状态N的过程中（）A.温度保持不变B.气体需要吸收热量C.外界对气体做功D.气体的密度在不断增大4.如题4图所示是A、B两物体从同一地点出发运动的x-t图象，图象A是一条直线，图象B 是抛物线，则下列说法正确的是（）A.物体B做曲线运动B.物体B初速度是10m/sC.物体A 所匀加速直线运动D.t =8s 时，两物体相遇 5.下列说法正确的是（ ）A.比结合能越大的原子核，核子平均质量越大B.10个235U 原子核经过一个半衰期后一定还剩下5个235U 原子核没发生衰变C.用频率一定的光照射某金属发生光电效应时，入射光强度越大，单位时间逸出的光电子数目越多D.汤姆孙首先发现了电子，从而说明原子核内有复杂的结构6.一群处于基态的氢原子吸收某种单色光子后，向外辐射了1ν、2ν、3ν三种频率的光子，且321ννν>>，则（ ） A.23:27:32νν=B.被氢原子吸收的光子能量为123()h ννν++C.用光子能量为12()h νν+的单色光照射处于基态的氢原子，可以使氢原子电离D.1ν、2ν、3ν三种频率的光子对应的波长分别为1λ、2λ、3λ，则有123λλλ=+ 7.在地面上方，将小球以4kg •m/s 的动量水平抛出，落地的动量大小是5kg•m/s ，不计空气阻力，g 取10m/s 2，则（ ） A.这过程中小球动量改变量为1kg•m/s B.这过程中小球重力做功为0.5JC.小球落地时速度方向和竖直方向的夹角是37°D.小球落地时重力瞬时功率为30W8.如题8图所示，某新修的笔直公路示意图，公路上每隔400m 设有一个红绿灯路口，各路口同时开启绿灯或同时关闭绿灯开启红灯，红绿灯转换时间不计，每一次绿灯持续时间为20s ，红灯持续时间为5s 。

湖南长郡中学、雅礼中学等四校联考2020年2月高考数学（理）试卷一、单选题 1．已知集合{}220A x xx =∈-++≥N ，则满足条件A B A ⋃=的集合B 的个数为( )A ．3B ．4C ．7D ．82．已知i 为虚数单位，,a b ∈R ，复数12ii a bi i+-=+-，则a bi -=（ ） A ．1255i - B ．1255i + C ．2155i -D ．21i 55+ 3．已知()1,2A ，()2,3B ，()1,C m -，若BA BC BA BC +=-u u u r u u u r u u u r u u u r ，则2AC =u u u r ( )A ．6B ．25C ．16D ．204．已知数列{}n a 满足211nn n aa a -+=（2n ≥），24804sin 2a a xdx π⋅=⎰，且40a >，则6tan 3a π⎛⎫⋅= ⎪⎝⎭( )A ．33-B ．33C ．3-D ．35．将函数()2sin 1f x x π=-的图象向左平移ϕ（102ϕ<<）个单位长度后得到函数()g x 的图象，若使()()4f a g b -=成立的a 、b 有min34a b -=，则下列直线中可以是函数()y g x =图象的对称轴的是( )A ．14x =- B ．12x=C ．34x = D ．54x =6．《海岛算经》中有这样一个问题，大意为：某粮行用芦席围成一个粮仓装满米，该粮仓的三视图如图所示（单位：尺，1尺0.33≈米），已知1斛米的体积约为1.62立方尺，圆周率约为3，则估算出该粮仓存放的米约为( )A ．43斛B ．45斛C ．47斛D ．49斛7．已知点G 在ABC ∆内，且满足2340GA GB GC++=u u u v u u u vu u u v v，现在ABC ∆内随机取一点，此点取自,,GAB GAC GBC ∆∆∆的概率分别记为123,,P P P ，则（ ） A ．123P P P ==B ．321P P P >>C ．123P P P >>D ．213P P P >>8．已知双曲线C ：22221x y a b-=（0a >，0b >）的右焦点为(),0F c ，点A 、B 分别在直线2a x c=-和双曲线C 的右支上，若四边形OABF （其中O 为坐标原点）为菱形且其面积为315，则a =( )A ．3B ．5C ．2D ．69．当x 为实数时，()trunc x 表示不超过x 的最大整数，如()trunc 3.13=.已知函数()()trunc f x x =（其中x ∈R ），函数()g x 满足()()6g x g x =-、()()11g x g x +=-，且[]0,3x ∈时，()22g x x x =-，则方程()()f x g x =的所有根的个数为( )A ．3B ．4C ．5D ．610．对四位数abcd （19a ≤≤，0b ≤、c ，9d ≤），若a b >、b c <、c d >，称abcd 为“吉祥数”，则“吉祥数”的个数为( ) A ．1695 B ．1696 C ．1697D ．169811．ABC ∆中，所有内角都不是钝角，有以下命题：①sin 2sin 2A B A B =⇔=；①sin 2sin 2A B A B >⇔<；①cos2cos2A B A B >⇔<；①sin cos A B ≥.其中正确命题的个数是( ) A ．1B ．2C ．3D ．412．如图所示，将3333⨯方格纸中每个小方格染三种颜色之一，使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同，称他们的公共边为“分割边”，则分割边条数的最小值为( )A ．33B ．56C ．64D ．78二、填空题13．若212nx x ⎛⎫- ⎪⎝⎭的展开式中第1r +项为常数项，则r n =______. 14．我国古代数学家祖暅提出原理：“幂势既同，则积不容异”.其中“幂”是截面积，“势”是几何体的高.原理的意思是：夹在两个平行平面间的两个几何体，被任一平行于这两个平行平面的平面所截，若所截的两个截面的面积恒相等，则这两个几何体的体积相等.如图(1)，函数()[)()(]2sin ,2,0211,0,2xx f x x x π⎧∈-⎪=⎨⎪--∈⎩的图象与x 轴围成一个封闭区域A （阴影部分），将区域A （阴影部分）沿z 轴的正方向上移6个单位，得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示，其底面积与区域A （阴影部分）的面积相等，则此柱体的体积为______.15．已知变量x 、y 满足约束条件0280260y x y x y ≥⎧⎪+-≤⎨⎪+-≥⎩，在实数x 、y 中插入7个实数，使这9个数构成等差数列{}n a 的前9项，则1a x =、9a y =，则数列{}n a 的前13项和的最大值为______.16．若有且仅有一个正方形，其中心位于原点，且其四个顶点在曲线3y x ax =+上，则实数a =______.三、解答题17．如图，多面体11ABC DB C -是正三棱柱（底面是正三角形的直棱柱）111ABC A B C -沿平面11DB C 切除一部分所得，其中平面ABC 为原正三棱柱的底面，12BC CC ==，点D 为1AA 的中点.(1)求证：1BC ⊥平面1B CD ；(2)求二面角1C BD C --的平面角的余弦值.18．已知椭圆C ：22221x y a b+=（0a b >>）的两焦点与短轴两端点围成面积为12的正方形.(1)求椭圆C 的标准方程；(2)我们称圆心在椭圆上运动，半径为222a b +的圆是椭圆的“卫星圆”.过原点O 作椭圆C 的“卫星圆”的两条切线，分别交椭圆C 于A 、B 两点，若直线OA 、OB 的斜率为1k 、2k ，当12210k k +=时，求此时“卫星圆”的个数.19．已知首项为1a 的数列{}n a 各项均为正数，且()()211224n n n n n n a a a a a +++-=，n *∈N .(1)若数列{}n b 的通项n b 满足2n n b a =，且11a =，求数列{}n b 的前n 项和为nT；(2)若数列{}n c 的通项n c 满足()4nn nb c S =，前n 项和为n Q ，当数列{}n c 是等差数列时，对任意的n *∈N ，均存在m *∈N ，使得24211816n a Q a n cm -=成立，求满足条件的所有整数1a 构成的集合.20．高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型，在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块，小木块之间留有适当的空隙作为通道，前面挡有一块玻璃，让一个小球从高尔顿板上方的通道口落下，小球在下落的过程中与层层小木块碰撞，且等可能向左或向右滚下，最后掉入高尔顿板下方的某一球槽内.如图所示的小木块中，上面7层为高尔顿板，最下面一层为改造的高尔顿板，小球从通道口落下，第一次与第2层中间的小木块碰撞，以12的概率向左或向右滚下，依次经过6次与小木块碰撞，最后掉入编号为1，2…，7的球槽内.例如小球要掉入3号球槽，则在前5次碰撞中有2次向右3次向左滚到第6层的第3个空隙处，再以12的概率向左滚下，或在前5次碰撞中有1次向右4次向左滚到第6层的第2个空隙处，再以12的概率向右滚下.(1)若进行一次高尔顿板试验，求小球落入第7层第6个空隙处的概率；(2)小明同学在研究了高尔顿板后，利用该图中的高尔顿板来到社团文化节上进行盈利性“抽奖”活动，8元可以玩一次高尔顿板游戏，小球掉入X 号球槽得到的奖金为ξ元，其中205X ξ=-.（i ）求X 的分布列：（ii ）高尔顿板游戏火爆进行，很多同学参加了游戏，你觉得小明同学能盈利吗？21．已知函数2()()af x x ax a R x=+-∈.（1）当1a =且1x >-时，求函数()f x 的单调区间； （2）当21e a e ≥+时，若函数2()()ln g x f x x x =--的两个极值点分别为1x 、2x ，证明12240()()1g x g x e <-<+.22．在直角坐标系xOy 中，曲线1C 的参数方程为2cos 62sin x y αα⎧=⎪⎨=+⎪⎩（α为参数），以坐标原点为极点，x 轴正半轴为极轴建立极坐标系，曲线2C 的极坐标方程为21019sin ρθ=+.(1)求曲线1C 的普通方程和2C 的直角坐标方程； (2)若M ，N 分别为曲线1C 和曲线2C 上的动点，求MN 的最大值.23．已知函数()2725f x x x =-+-.(1)解不等式()6f x ≥；(2)设函数()f x 的最小值为m ，已知正实数a ，b ，且221max ,a b k a b a b ⎧⎫+=⎨⎬++⎩⎭，证明：21k m ≥.解析湖南长郡中学、雅礼中学等四校联考2020年2月高考数学（理）试卷一、单选题 1．已知集合{}220A x xx =∈-++≥N ，则满足条件A B A ⋃=的集合B 的个数为( )A ．3B ．4C ．7D ．8【答案】D【解析】可以求出集合{}0,1,2A =，由A B A ⋃=可得B A ⊆，从而求集合A 的子集个数即可. 解：{}{}2200,1,2A x xx =∈-++≥=N ，∵A B A ⋃=，∵B A ⊆，∵集合A 的子集个数为328=个.故选：D.【点睛】本题考查并集的运算及理解，是基础题. 2．已知i 为虚数单位，,a b ∈R ，复数12ii a bi i+-=+-，则a bi -=（ ） A ．1255i - B ．1255i + C ．2155i - D ．21i 55+ 【答案】B【解析】由复数的除法运算，可得(1)(2)12(2)(2)55i i i i i i a b i=+++-=--+，即可求解a b i -，得到答案． 由题意，复数12ii a bi i+-=+-，得(1)(2)1312(2)(2)555i i a b i=i i i i i i ++++-=-=--+， 所以1255a b i=i -+，故选B ． 【点睛】本题主要考查了复数的运算，其中解答中熟记复数的基本运算法则，准确化简是解答的关键，着重考查了推理与运算能力，属于基础题．3．已知()1,2A ，()2,3B ，()1,C m -，若BA BC BA BC +=-u u u r u u u r u u u r u u u r ，则2AC =u u u r ( )A ．6B ．25C ．16D ．20【答案】D【解析】代入坐标可求出(4,4),(2,2)BA BC m BA BC m +=---=-u u u r u u u r u u u r u u u r，利用模的坐标运算列方程可得6m =，进而可求出AC u u u r 的坐标，则2AC u u u r 可求.【详解】解：(1,1),(3,3)BA BC m =--=--u u u r u u u r ，(2,2)CA m =-u u u r， (4,4),(2,2)BA BC m BA BC CA m ∴+=---==-u u u r u u u r u u u r u u u r u u u r， 又BA BC BA BC +=-u u u r u u u r u u u r u u u r，2216(4)4(2)m m ∴+-=+-，解得6m =，(2,4)AC ∴=-u u u r ，241620AC ∴=+=u u u r.故选：D.【点睛】考查根据点的坐标求向量的坐标的方法，向量坐标的加法运算，向量减法的几何意义，以及根据向量坐标求向量长度的方法，是基础题. 4．已知数列{}n a 满足211nn n aa a -+=（2n ≥），24804sin 2a a xdx π⋅=⎰，且40a >，则6tan 3a π⎛⎫⋅= ⎪⎝⎭( )A ．33-B ．33C ．3-D ．3【答案】C【解析】由211n n n a a a -+=（2n ≥），可知数列{}n a 是等比数列，利用微积分基本定理可求得20sin21xdx π=⎰，从而可求得24864a a a ⋅== ，而由40a >可知62a =，从而可求得答案.【详解】解：由211n n n a a a -+=（2n ≥），知数列{}n a 是等比数列，又20111sin 2cos 2122220xdx x ππ=-=+=⎰，所以24864a a a ⋅==，又40a >，所以60a >，所以62a =，所以则62tan tan 333a ππ⎛⎫⋅==- ⎪⎝⎭. 故选：C. 【点睛】本题考查数列递推式的应用，考查微积分基本定理及等比数列的性质，求得62a =是关键，考查运算求解能力，属于中档题. 5．将函数()2sin 1f x x π=-的图象向左平移ϕ（102ϕ<<）个单位长度后得到函数()g x 的图象，若使()()4f a g b -=成立的a 、b 有min34a b -=，则下列直线中可以是函数()y g x =图象的对称轴的是( )A ．14x =- B ．12x =C ．34x = D ．54x =【答案】D【解析】根据三角函数平移关系求出()gx 的解析式，结合()()4f a g b -=成立的,a b 有min 34a b -=，求出,a b 的关系，结合最小值建立方程求出ϕ的值即可. 【详解】 解：将函数()2sin 1f x x π=-的图象向左平移ϕ（102ϕ<<）个单位长度后得到函数()g x 的图象，即()2sin ()1g x x πϕ=+-， 若()()4f a g b -=成立，即|2sin 2sin (+)|=4a b ππϕ-， 即|sin sin ()|2a b ππϕ-+=，则sin a π与sin ()b πϕ+一个取最大值1，一个取最小值−1， 不妨设sin 1,sin ()1a b ππϕ=+=-， 则2,,()2,22a k k Zb n n Z πππππϕπ=+∈+=-∈，得112,222a kb n ϕ=+=--， 则2()1a b k n ϕ-=-++，∵min34a b -=， ∵当0k n -=时，3||11,2a b ϕ⎛⎫-=+∈ ⎪⎝⎭， 当1k n -=-时，1|||1|,12a b ϕ⎛⎫-=-∈ ⎪⎝⎭，3|1|4ϕ∴-=，则314ϕ-=或314ϕ-=-，即14ϕ=或74ϕ=（舍），即1()2sin 12sin 144g x x x πππ⎛⎫⎛⎫=+-=+- ⎪ ⎪⎝⎭⎝⎭，由,42x k k Z ππππ+=+∈，得1,4x k k Z =+∈， 当1k=时，对称轴方程为54x =.【点睛】本题考查三角函数的图象平移，以及三角函数的图象和性质，结合三角函数的最值性建立方程关系求出,a b 的大小，结合最小值求出ϕ的值是解决本题的关键.考查分析问题解决问题的能力，有一定难度.6．《海岛算经》中有这样一个问题，大意为：某粮行用芦席围成一个粮仓装满米，该粮仓的三视图如图所示（单位：尺，1尺0.33≈米），已知1斛米的体积约为1.62立方尺，圆周率约为3，则估算出该粮仓存放的米约为( )A ．43斛B ．45斛C ．47斛D ．49斛【答案】D【解析】首先判断该几何体的形状，然后根据其体积计算公式计算即可. 【详解】解：观察发现该几何体为圆台和圆柱的结合体， 其体积为：2221179262211333ππππ⨯⨯+⨯⨯⨯-⨯⨯⨯=（尺）， 则该粮仓存放的米约为793 1.62493⨯÷≈（斛）. 故选：D. 【点睛】考查了由三视图判断几何体的知识，解题的关键是首先判断几何体的形状，难度不大.7．已知点G 在ABC ∆内，且满足2340GA GB GC ++=u u u v u u u vu u u v v，现在ABC ∆内随机取一点，此点取自,,GAB GAC GBC ∆∆∆的概率分别记为123,,P P P ，则（ ）A ．123P P P ==B ．321P P P >>C ．123P P P >>D ．213P P P >>【答案】C【解析】分别延长GA 到GA '，GB 到GB '，GC 到GC '，使得2GA GA '=，3GB GB '=，4GC GC '=，则有0GA GB GC '''++=u u u r u u u r u u u u r，得到点G 为A B C '''∆的重心，所以GA B GA C GB C S S S ''''''∆∆∆==，进而求得16GAB GA B S S ''∆∆=，18GAC GAC S S '∆∆=，112GBC GB C S S '∆∆=，得出面积之间的关系，即可求解．由题意，分别延长GA 到GA '，GB 到GB '，GC 到GC '，使得2GA GA '=，3GB GB '=，4GC GC '=，则有0GA GB GC '''++=u u u r u u u r u u u u r， 所以点G 为A B C '''∆的重心，所以GA B GA C GB C S S S ''''''∆∆∆==， 又16GABGA B S S ''∆∆=，18GAC GAC S S '∆∆=，112GBC GB C S S '∆∆=， 从而得到::GAB GAC GBC S S S ∆∆∆=111::4:3:26812=， 则123:P :4:3:2P P =，即123P P>>P .故选C. 【点睛】本题主要考查了平面向量的应用，以及几何概型思想的应用，其中解答中根据响亮的运算求得点G 的位置，得出面积之间的关系是解答的关键，着重考查了推理与运算能力，属于中档试题．8．已知双曲线C ：22221x y a b-=（0a >，0b >）的右焦点为(),0F c ，点A 、B 分别在直线2a x c=-和双曲线C 的右支上，若四边形OABF （其中O 为坐标原点）为菱形且其面积为315，则a =( )A ．3B ．5C ．2D ．6【答案】A【解析】设点2,a A t c ⎛⎫-⎪⎝⎭，0t >，因为OF AB c ==，则2,a B c t c ⎛⎫-+ ⎪⎝⎭，根据点B 在双曲线上可得一个关于,,a b c 方程，根据面积又可得一个关于,,a b c 的方程，在加上222c a b -=，列方程求解即可. 【详解】 解：如图：设点2,a A t c ⎛⎫-⎪⎝⎭，0t >，因为OF AB c ==，则2,a B c t c ⎛⎫-+ ⎪⎝⎭， 又OB AF ⊥，则221tta ac c c c⋅=--+--，化简得2222(1)a t b c=+，222,1a a B c b c c ⎛⎫∴-++ ⎪ ⎪⎝⎭2222222(1)1a a c b c c a b ∴-⎛⎫-+ +⎝⎭=⎪∵ ， 又221315122a cbc ⨯⨯+=∵， 222c a b -=∵，∵由∵∵∵得3,3,23a b c ===.故选：A. 【点睛】本题考查双曲线的性质的应用，考查学生计算能力，根据条件列方程是本题的关键，是中档题. 9．当x 为实数时，()trunc x 表示不超过x 的最大整数，如()trunc 3.13=.已知函数()()trunc f x x =（其中x ∈R ），函数()g x 满足()()6g x g x =-、()()11g x g x +=-，且[]0,3x ∈时，()22g x x x =-，则方程()()f x g x =的所有根的个数为( )A ．3B ．4C ．5D ．6【答案】D【解析】由()()6g x g x =-，()()11g x g x +=-，得函数()g x 的图象关于直线1x =及直线3x =对称，又由()()()(2)624g x g x g x g x ⎡⎤=-=--=+⎣⎦可得()g x 的周期，通过作图观察的方法可得结果. 【详解】解：由()()6g x g x =-，()()11g x g x +=-，得函数()gx 的图象关于直线1x =及直线3x =对称，()()()(2)624g x g x g x g x ⎡⎤∴=-=--=+⎣⎦，则()gx 为周期函数，且最小正周期为4. 对于()f x ，当[0,1)x ∈时，()0f x =当[1,2)x ∈时，()1f x =；当[2,3)x ∈时，()2f x =； 当[3,4)x ∈时，()3f x =； 当[4,5)x ∈时，()4f x =； …；当[1,0)x ∈-时，()1f x =； 当[2,1)x ∈--时，()2f x =； 当[3,2)x ∈--时，()3f x =； 当[4,3)x ∈--时，()4f x =； 当[5,4)x ∈--时，()5f x =；…综合已知条件可在同一直角坐标系内画出函数()f x 及()g x 的图象，由图可知，函数()y f x =与函数()y g x =共有6个交点，即方程()()f x g x =的根的个数为6.故选：D. 【点睛】此题考查了函数的图象和性质，由数形结合求解，画出函数的图像很关键，是中档题. 10．对四位数abcd （19a ≤≤，0b ≤、c ，9d ≤），若a b >、b c <、c d >，称abcd 为“吉祥数”，则“吉祥数”的个数为( ) A ．1695 B ．1696 C ．1697 D ．1698【答案】A【解析】由数的特点，先确定,b d 位置上的数，再安排,a c 位置上的数，列举出来算出个数即可. 【详解】解：由数的特点，先确定,b d 位置上的数，再安排,a c 位置上的数，列表如下： 其中第一列是d 取的数，第一行是b 取的数，中间是满足吉祥数的,a c 组合的数量， 如：0,0b d ==，,a c 组合有99⨯种可能，则吉祥数的个数为：9(987654321)8(887654321)⨯+++++++++⨯++++++++7(777654321)1(111111111)+⨯+++++++++⋯+⨯++++++++945844742639217191695=⨯+⨯+⨯+⨯+⋯+⨯+⨯=，故选：A. 【点睛】本题考查列表分类求数量，关键是要在列举中发现规律，进而方便计算出结果，是中档题. 11．ABC ∆中，所有内角都不是钝角，有以下命题：①sin 2sin 2A B A B =⇔=；①sin 2sin 2A B A B >⇔<；①cos2cos2A B A B >⇔<；①sin cos A B ≥.其中正确命题的个数是( ) A ．1 B ．2C ．3D ．4【答案】C【解析】利用三角公式变形和三角函数的性质逐一判断. 【详解】解：∵sin 2sin 2A B =，则22A B =或22A B π+＝，则A B =或A B π+＝２，故错误；∵()()()()sin 2sin 2sin sin A B A B A B A B A B =++-+--⎡⎤⎡⎤⎣⎦⎣⎦－－()()()2cos sin 0sin 00A B A B A B A B A B =+->⇔-<⇔-<⇔<，故正确；∵()()()()cos 2cos 2cos cos A B A B A B A B A B -=++--+--⎡⎤⎡⎤⎣⎦⎣⎦()()()2sin sin 0sin 00A B A B A B A B A B =-+->⇔-<⇔-<⇔<，故正确；∵sin cos sin sin +222A B A B A B A B πππ⎛⎫≥⇔≥-⇔≥-⇔≥ ⎪⎝⎭，故正确.故选：C. 【点睛】本题考查三角形中角的关系的判断，考查应用公式变形的熟练程度，是中档题.12．如图所示，将3333⨯方格纸中每个小方格染三种颜色之一，使得每种颜色的小方格的个数相等.若相邻两个小方格的颜色不同，称他们的公共边为“分割边”，则分割边条数的最小值为( )A ．33B ．56C ．64D ．78【答案】B【解析】记分隔边的条数为L ，首先将方格按照按图分三个区域，分别染成三种颜色，粗线上均为分隔边，将方格的行从上至下依次记为1233,,,A A A L ，列从左至右依次记为1233,,B B B L ，行j c 中方格出现的颜色数记为()i n A ，列i B 中方格出现的颜色个数记为()i n B ，三种颜色分别记为123,,c c c ，对于一种颜色j c ，设()j n c 为含有j c 色方格的行数与列数之和，定义当i A 行含有jc 色方格时，(),1ijA c δ=，否则(),0ijA c δ=，类似的定义(),ijB c δ，计算得到()()()3311()i i j i j n A n B n c ==+=∑∑３，再证明()39(1,2,3)jn c j ≥=，再证明对任意133i ≤≤均有()()2,2i i nA nB ≥≥，最后求出分隔边条数的最小值.【详解】记分隔边的条数为L ，首先将方格按照按图分三个区域，分别染成三种颜色，粗线上均为分隔边，此时共有56条分隔边，即56L =， 其次证明：56L ≥，将将方格的行从上至下依次记为1233,,,A A A L ，列从左至右依次记为1233,,B B B L ，行i A 中方格出现的颜色数记为()i n A ，列i B 中方格出现的颜色个数记为()i n B ，三种颜色分别记为123,,c c c ，对于一种颜色j c ，设()j n c 为含有j c 色方格的行数与列数之和，定义当i A 行含有jc 色方格时，(),1ijA c δ=，否则(),0ijA c δ=，类似的定义(),ijB c δ，所以()()()()()()()3333331111,,iiiji j j i i i j n A n B A c B c n c δδ====⎫+=+=⎪⎭∑∑∑∑，由于染j c 色的格有21333633⨯=个，设含有j c 色方格的行有a 个，列有b 个，则j c 色的方格一定再这个a 行和b 列的交叉方格中，从而363ab ≥， 所以()()223633839(1,2,3)j j nc a b ab n c j =+≥≥>⇒≥=∵，由于在行i A 中有()i n A 种颜色的方格，于是至少有()1i n A -条分隔边， 类似的，在列i B 中有()i n B 种颜色的方格，于是至少有()1i n B -条分隔边， 则()()()()()()()3333113311166iiiii i i L n A n B n A n B ===≥-+-=+-∑∑∑∵()3166j j n c ==-∑∵下面分两种情形讨论，(1)有一行或一列所有方格同色，不妨设有一行均为1c 色，则方格的33列均含有1c 的方格，又1c 色的方格有363个,故至少有11行有1c 色方格，于是()1113344n c ≥+=∵由∵∵∵得()()()123664439396656L n c n c n c ≥++-≥++-=，(2)没有一行也没有一列的所有方格同色, 则对任意133i ≤≤均有()()2,2i i n A n B ≥≥，从而，由式∵知：()()()33166334666656i i i L n A n B =≥+-≥⨯-=>∑，综上，分隔边条数的最小值为56. 故选：B. 【点睛】本题主要考查染色问题，考查计数原理，考查分析推理能力，是一道难度极大的题目. 二、填空题13．若212nx x ⎛⎫- ⎪⎝⎭的展开式中第1r +项为常数项，则r n =______. 【答案】23【解析】由题意利用二项展开式的通项公式，求得320r n -=，从而得到rn的值. 【详解】解：212nx x ⎛⎫- ⎪⎝⎭的展开式中第1r +项为 .321(1)2n r r r r n n C x ⋅--⎛⎫⋅- ⎪⎝⎭，再根据它为常数项，可得320r n -=，求得23r n =，故答案为：23.【点睛】本题主要考查二项式定理的应用，二项展开式的通项公式，二项式系数的性质，属于基础题. 14．我国古代数学家祖暅提出原理：“幂势既同，则积不容异”.其中“幂”是截面积，“势”是几何体的高.原理的意思是：夹在两个平行平面间的两个几何体，被任一平行于这两个平行平面的平面所截，若所截的两个截面的面积恒相等，则这两个几何体的体积相等.如图(1)，函数()[)()(]2sin ,2,0211,0,2xx f x x x π⎧∈-⎪=⎨⎪--∈⎩的图象与x 轴围成一个封闭区域A （阴影部分），将区域A （阴影部分）沿z 轴的正方向上移6个单位，得到一几何体.现有一个与之等高的底面为椭圆的柱体如图(2)所示，其底面积与区域A （阴影部分）的面积相等，则此柱体的体积为______.【答案】243ππ+【解析】阴影区域在(0,2]上为半个圆，所以柱体的底面积为半圆的面积减去函数()f x 在[2,0)-上的积分，有了底面积，又知道高为6，即可得到柱体的体积.【详解】解：由题意得，阴影区域在(0,2]上为半个圆， 底面积12SS =圆0022124sin cos |2222x x dx ππππππ---=+=+⎰，所以该柱体的 体积为424632ππππ⎛⎫+⨯=+ ⎪⎝⎭. 故答案为：243ππ+.【点睛】本题考查定积分在求曲边梯形面积上的应用，考查计算能力.15．已知变量x 、y 满足约束条件0280260y x y x y ≥⎧⎪+-≤⎨⎪+-≥⎩，在实数x 、y 中插入7个实数，使这9个数构成等差数列{}n a 的前9项，则1a x =、9a y =，则数列{}n a 的前13项和的最大值为______.【答案】2216【解析】画出约束条件表示的平面区域，结合图形计算该等差数列{}n a 的公差d ，写出数列{}n a 的前13项和13S ，求出它的最大值.【详解】解：画出约束条件0280260y x y x y ≥⎧⎪+-≤⎨⎪+-≥⎩表示的平面区域，如图所示；解方程组280260x y x y +-=⎧⎨+-=⎩，得410,33A ⎛⎫⎪⎝⎭；记这个等差数列为{}n a ，其公差为d ，则1()918y x dy x -==--， 所以数列{}n a 的前13项和为()()1131371136()131313613(3)284a a y x S a a d x x y +-⎡⎤===+=+=+⎢⎥⎣⎦， 作出直线:30l x y +=，由图形可知，当直线l 过点A 时，3z x y =+取得最大值，所以13S 的最大值为134********⎛⎫⨯+= ⎪⎝⎭.故答案为：2216. 【点睛】本题考查了二元一次不等式组表示平面区域应用问题，也考查了等差数列应用问题，是中档题. 16．若有且仅有一个正方形，其中心位于原点，且其四个顶点在曲线3y x ax =+上，则实数a =______.【答案】22-【解析】设正方形ABCD 对角线AC 所在的直线方程为y kx =，则其斜率唯一确定，转化为二元方程只有唯一实数根，利用根的判别式求解即可. 【详解】解：设正方形ABCD 对角线AC 所在的直线方程为,0y kx k =≠， 则对角线BD 所在的直线方程为1=-y x k. 由3y kx y x ax=⎧⎨=+⎩，解得2x k a =-， 所以()()()22222211x y k k A x k a O =+=+=+-，同理，222211111k a a k kO k B k ⎡⎤+⎛⎫⎛⎫⎛⎫=+-⋅--=-⋅+⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦， 又因为22AO BO =，所以3210a k k a k -++=，即22110k a k k k ⎛⎫+--= ⎪⎝⎭，即21120k a k k k ⎛⎫⎛⎫---+= ⎪ ⎪⎝⎭⎝⎭. 令1k t k-=得220t at -+=，因为正方形ABCD 唯一确定，则对角线AC 与BD 唯一确定，于是1k k-值唯一确定，所以关于t 的方程220t at -+=有且只有一个实数根，又1k t R k-=∈.所以280a ∆=-=，即22a =±， 因为20x k a =->，所以a k <；又10a k -->，所以1a k <-，故0a <. 因此22a =-；反过来22a =-时，12,2t k k=--=-，于是26126,22k k -+--=-=；或26126,22k k ---+=-=. 于是正方形ABCD 唯一确定. 故答案为：22-.【点睛】本小题主要考查函数的解析式的求法以及二次函数的性质，考查综合利用数学知识分析问题、解决问题的能力.三、解答题17．如图，多面体11ABC DB C -是正三棱柱（底面是正三角形的直棱柱）111ABC A B C -沿平面11DB C 切除一部分所得，其中平面ABC 为原正三棱柱的底面，12BC CC ==，点D 为1AA 的中点.(1)求证：1BC ⊥平面1B CD ；(2)求二面角1C BD C --的平面角的余弦值. 【答案】(1)证明见解析；(2)64.【解析】（1）设1BC 与1B C 交于点E ，连接DC 、DE ，由题意可得四边形11BB C C 是正方形，且AC AD ⊥，再由点D 为1AA 的中点，1AA 平行且等于1CC ，求得CD ，同理求得1DB ，得1DB CD =，可得1B C DE ⊥，由线面垂直的判定可得；（2）取BC 的中点O ，连接AO ，可得AO ∵BC ，由正棱柱的性质可得AO ∵平面11BCC B ，以O为坐标原点，向量OB uuu r 、OE uuu r 、OA u u u r分别为x 、y ，z 轴建立空间直角坐标系，分别求出平面CBD 与平面1BC D 的一个法向量，由两法向量所成角的余弦值可得二面角1C BD C --的平面角的余弦值. 【详解】(1)设1BC 与1B C 交于点E ，连接DC 、DE .∵多面体11ABC DB C -是正三棱柱沿平面11DB C 切除部分所得，12BC CC ==， ∵四边形11BB C C 是正方形，且ACAD ⊥.∵点D 为1AA 的中点，1AA 平行且等于1CC ， ∵225CD CA AD =+=.同理()22115DB BB AD AB =-+=，∵1DB CD =.∵E 为1B C 的中点，∵1B CDE ⊥.又∵11B C BC ⊥，1BC DE E =I ，∵1B C⊥平面1BC D ；(2)取BC 的中点O ，连接AO . ∵ABC V 为正三角形，AO BC ∴⊥.由正棱柱的性质可得，平面ABC ⊥平面11BCC B ， 且平面ABC I 平面11BCC B BC =， ∵AO ⊥平面11BCC B .以点O 为原点，向量OB uuu r 、OE uuu r 、OA u u u r分别为x 、y ，z 轴正方向建立如图所示空间直角坐标系Oxyz . 则()1,0,0B ，()11,2,0B ，()1,0,0C -，()0,1,3D ，()1,1,3CD ∴=u u u r ，()1,1,3BD =-u u u r ，()12,2,0B C =--u u u r.设平面CBD 的一个法向量为(),,n x y z =r，则3030n BD x y z n CD x y z ⎧⋅=-++=⎪⎨⋅=++=⎪⎩u u u v v u u u v v ， 令1z =，得0x =，3y =-，即()0,3,1n =-r.由（1）可知，平面1BC D 的一个法向量为()12,2,0B C =--u u u r.()()()10232106cos ,41344n B C ⨯-+-⨯-+⨯∴==+⨯+r u u u r ，又∵二面角1C BD C --的平面角为锐角， ∵二面角1C BDC --的平面角的余弦值为64.【点睛】本题考查直线与平面垂直的判定，考查空间想象能力与思维能力，训练了利用空间向量求解二面角的大小，是中档题.18．已知椭圆C ：22221x y a b+=（0a b >>）的两焦点与短轴两端点围成面积为12的正方形.(1)求椭圆C 的标准方程；(2)我们称圆心在椭圆上运动，半径为222a b +的圆是椭圆的“卫星圆”.过原点O 作椭圆C 的“卫星圆”的两条切线，分别交椭圆C 于A 、B 两点，若直线OA 、OB 的斜率为1k 、2k ，当12210k k +=时，求此时“卫星圆”的个数.【答案】(1)221126x y +=；(2)8个.【解析】(1)由条件可得212b cbc =⎧⎨=⎩，解出来即可；(2) 设“卫星圆”的圆心为()00,x y ，由定义可得“卫星圆”的标准方程为()()22009x x y y -+-=，求其圆心到直线OA ，直线OB 的距离，整理可转化为1k 、2k 是方程()22200009290x k x y k y --+-=的两个不相等的实数根，则00122029x y k k x +=-，再加上12210k k +=，22001126x y +=，解方程即可.【详解】(1)∵椭圆C 的两焦点与短轴两端点围成面积为12的正方形， ∵由椭圆的定义和正方形的性质，可得212b cbc =⎧⎨=⎩，解得6b c ==.又22212a b c =+=∵椭圆C 的标准方程为221126x y +=.(2)设“卫星圆”的圆心为()00,x y .由“卫星圆”的定义，可得“卫星圆”的半径为2232a b+=.∵“卫星圆”的标准方程为()()22009x x y y -+-=.∵直线OA ：1y k x =与“卫星圆”相切，则由点到直线的距离公式可1002131k x y k-=+，化简得()222100109290xk x y k y --+-=.同理可得()222200209290xk x y k y --+-=.∵1k 、2k 是方程()2220009290xk x y k y --+-=的两个不相等的实数根，∵2090x -≠，由>0∆，得22009x y +>，将22001126x y +=代入得206x >，00122029x y k k x +=-. 又∵“卫星圆”的圆心()00,x y 在椭圆C 上，∵代入椭圆方程221126x y +=中，可得22001126x y +=.解得22062x y =-，()()()()220022242000012222222000462424240999x x x y x x k k x x x ⎛⎫- ⎪-⎝⎭∴+====---. 当2010x =时，201y =；当20547x =时，20157y =， ∵满足条件的点()00,x y 共8个，∵这样“卫星圆”存在8个. 【点睛】本题考查椭圆方程的求解，考查直线和椭圆的位置关系，注意韦达定理的应用，考查计算能力与分析能力，是一道中档题. 19．已知首项为1a 的数列{}n a 各项均为正数，且()()211224n n n n n n a a a a a +++-=，n *∈N .(1)若数列{}n b 的通项n b 满足2n n b a =，且11a =，求数列{}n b 的前n 项和为nT；(2)若数列{}n c 的通项n c 满足()4nn nb c S =，前n 项和为n Q ，当数列{}n c 是等差数列时，对任意的n *∈N ，均存在m *∈N ，使得24211816n a Q a n cm -=成立，求满足条件的所有整数1a 构成的集合.【答案】(1)()31419n nn T -+=；(2)112,,,m m a a n m n n ***⎧⎫⎪⎪=∈∈∈⎨⎬⎪⎪⎩⎭N N N . 【解析】(1)由条件可变形为121n n a a n n +=+，可得数列n a n ⎧⎫⎨⎬⎩⎭是以1a 为首项，以2为公比的等比数列，进而可得112n n a a n -=，则214n n n b a n -==⋅，再利用错位相减法求和即可；(2)根据(1)求出2114a c S =，222216a c S =，233364a c S=，由数列{}n c 是等差数列，列方程可得1S =或3S =，分1S =和3S =讨论，通过条件对任意的n *∈N ，均存在m *∈N ，使得24211816n m a Q a n c -=成立，可得1a .【详解】 (1)∵数列{}n a 各项均为正数，且()()211224n n n n n n a a a a a +++-=，()22141n n n a na +∴+=，即121n n n a na ++=，即121n n a an n+=+. ∵数列n a n ⎧⎫⎨⎬⎩⎭是以1a 为首项，以2为公比的等比数列， 112n na a n-∴=⋅， ∵数列{}n a 的通项公式为112n n a a n -=.∵11a =，∵214n n n b a n -==⋅，∵01211424344n n T n -=⨯+⨯+⨯++⨯L ，12341424344n n T n =⨯+⨯+⨯++⨯L ，两式相减，得0121344444n nn T n --=++++-⋅L 14414n nn -=-⋅-1443n n n -=-⋅-，()31419n nn T -+∴=， ∵数列{}n b 的前n 项和()31419n nn T -+=； (2)∵数列{}n c 的通项()4nn nb c S =，∵由(1)得，()24nn na c S =，∵2114a c S =，222216a c S =，233364a c S=.又数列{}n c 是等差数列，∵22232123216464a a a S S S=+. 22211121648416a a a S S∴=+，即2430S S -+=. 解得1S =或3S =.又()21144n n nna c S -⋅=，∵当1S =时，214n na c =，{}n c 为等差数列，2211442n a na n Q ⎛⎫+ ⎪⎝⎭=()22118n a na +=对任意的n *∈N ，均存在m *∈N ，使得24211816n m a Q a n c -=成立，()2221124211181684n a na ma a a n +∴⋅-=⋅，214na m ∴=，12m a n∴=. 又1a 为正整数，∵满足条件的所有整数1a 的值构成的集合为112,,,m m a a n m n n ***⎧⎫⎪⎪=∈∈∈⎨⎬⎪⎪⎩⎭N N N . 当3S =时，2143n n na c =⨯，()21111243n n n n a c c ++--=⨯Q 不是常数， ∵数列{}n c 不是等差数列，舍去.综上，满足条件的所有整数1a 的值构成的集合为112,,,m m a a n m n n ***⎧⎫⎪⎪=∈∈∈⎨⎬⎪⎪⎩⎭N N N . 【点睛】本题考查由递推式求通项公式，考查错位相减法求和，考查数列中的存在性，任意性的问题，考查计算能力，是一道难度较大的题目.20．高尔顿板是英国生物统计学家高尔顿设计用来研究随机现象的模型，在一块木板上钉着若干排相互平行但相互错开的圆柱形小木块，小木块之间留有适当的空隙作为通道，前面挡有一块玻璃，让一个小球从高尔顿板上方的通道口落下，小球在下落的过程中与层层小木块碰撞，且等可能向左或向右滚下，最后掉入高尔顿板下方的某一球槽内.如图所示的小木块中，上面7层为高尔顿板，最下面一层为改造的高尔顿板，小球从通道口落下，第一次与第2层中间的小木块碰撞，以12的概率向左或向右滚下，依次经过6次与小木块碰撞，最后掉入编号为1，2…，7的球槽内.例如小球要掉入3号球槽，则在前5次碰撞中有2次向右3次向左滚到第6层的第3个空隙处，再以12的概率向左滚下，或在前5次碰撞中有1次向右4次向左滚到第6层的第2个空隙处，再以12的概率向右滚下.(1)若进行一次高尔顿板试验，求小球落入第7层第6个空隙处的概率；(2)小明同学在研究了高尔顿板后，利用该图中的高尔顿板来到社团文化节上进行盈利性“抽奖”活动，8元可以玩一次高尔顿板游戏，小球掉入X 号球槽得到的奖金为ξ元，其中205X ξ=-.（i ）求X 的分布列：（ii ）高尔顿板游戏火爆进行，很多同学参加了游戏，你觉得小明同学能盈利吗？ 【答案】(1)332；(2)（i ）分布列见解析；（ii ）能盈利. 【解析】（1）记小球落入第7层第6个空隙处的事件为M ，小球落入第7层第6个空隙处，需要在6次碰撞中有1次向左5次向右，由此能求出这个小球掉入第7层第6个空隙处的概率； （2）X 的取值为1，2，3，4，5，6，7，由此能求出X 的分布列，进而可求出ξ的分布列和E ξ，从而能求出小明同学能盈利. 【详解】(1)记小球落入第7层第6个空隙处的事件为M ，小球落入第7层第6个空隙处，需要在6次碰撞中有1次向左5次向右，则()5161132232P M C ⎛⎫⎛⎫== ⎪⎪⎝⎭⎝⎭； (2)（i ）由已知X 的取值可为1，2，3，4，5，6，7.()()0606111722641P X P X C ⎛⎫⎛⎫==== ⎪⎝⎭=⎪⎝⎭；()()1516116326226432P X P X C ⎛⎫⎛⎫====== ⎪⎪⎝⎭⎝⎭； ()()24261115352264P X P X C ⎛⎫⎛⎫===== ⎪ ⎪⎝⎭⎝⎭； ()3336112054226416P X C ⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭， ∵X 的分布列为 X1234567P 116 332 1564 516 1564 332 116（ii ）205Xξ=-Qξ∴的可能取值为0，5，10，15，()()50416P P X ξ====， ()()()1553532P P X P X ξ===+==， ()()()3102616P P X P X ξ===+==， ()()()1151732P P X P X ξ===+==， ∵()515317505101581632163216E ξ=⨯+⨯+⨯+⨯=<. ∵小明同学能盈利. 【点睛】本题考查概率的求法，考查离散型随机变量的分布列和数学期望的求法，解题时要认真审题，注意排列组合知识的合理运用. 21．已知函数2()()af x x ax a R x=+-∈.（1）当1a =且1x >-时，求函数()f x 的单调区间； （2）当21e a e ≥+时，若函数2()()ln g x f x x x =--的两个极值点分别为1x 、2x ，证明12240()()1g x g x e <-<+. 【答案】（1）()f x 的单调递增区间为()(1,0),0,-+∞，；无单调递减区间；（2）证明见解析.【解析】(1)求得3222121()21x x f x x x x++'=++=，分类讨论，即可求解()f x 的单调区间，得到答案；(2)根据12,x x 是函数()g x '的两个零点，设12,x x 是方程20ax x a -+=的两个实数解，再根据二次函数的性质函数()g x 在1x 处取得极大值,在2x 处取得极小值，进而得到1211x a x =+，代入得()()22112121112ln 12x g x g x x x ⎛⎫--=- ⎪+⎝⎭，令21x t =，则211t e <<，得到11()2ln 12t g t t t -⎛⎫=-⎪+⎝⎭，设11()2ln 12x h x x x -⎛⎫=-⎪+⎝⎭，利用导数求得函数的单调性与最值，即可求解． 【详解】(1)由题意，当1a =时，21()f x x x x =+-，3222121()21x x f x x x x'++∴=++=， ∵当0x>时，()0f x '>恒成立，所以函数()f x 在区间(0,)+∞上单调递增； ∵当10x -<<时，记32()21x x x ϕ=++，则21()6263x x x x x ϕ'⎛⎫=+=+⎪⎝⎭， 所以当1,03x ⎛⎫∈- ⎪⎝⎭时，()0x ϕ'<，∵()x ϕ单调递减，且()(0)1x ϕϕ>=；当11,3x ⎛⎫∈-- ⎪⎝⎭时，()0x ϕ'>，()x ϕ单调递增，且(1)0ϕ-=，所以当(1,0)x ∈-时，()0x ϕ>，函数()f x 单调递增.综上所述，函数()f x 的单调递增区间为(1,0)-，(0,)+∞；无单调递减区间. (2)由2()()ln ln (R,0)ag x f x x x ax x a x x=--=--∈>， 2221()a ax x ag x a x x x'-+∴=+-=， 12,x x Q 是函数()g x '的两个零点，12,x x ∴是方程20ax x a -+=的两个实数解，由0>∆，且21e a e >+，得2112e a e <<+，则有121x x =， 不妨设12x x <，1201x x ∴<<<。

长郡中学高三停课不停学第二次阶段性检测理科综合能力测试二、选择题：本题共8小题，每小题6分。

在每小题给出的四个选项中，第14~18题只有一项符合题目要求，第19~21题有多项符合题目要求。

全部选对的得6分，选对但不全的得3分，有选错的得0分。

14. 与下列图片相关的物理知识说法正确的是A.甲图，汤姆生通过α粒子散射实验，提出了原子核的概念，建立了原子核式结构模型B.乙图，氢原子的能级结构图，一个处于n=4能级的氢原子向低能级跃迁时，能辐射6 种不同频率的光子C.丙图，“光电效应”实验揭示了光的粒子性，爱因斯坦为此提出了光子说，建立了光电效应方程D.丁图，重核裂变产生的中子能使核裂变反应连续的进行，称为链式反应，其中一种核裂变反应方程为235141921 9256360 U Ba2Kr n →++15. 如图所示，曲线I是一颗绕地球做圆周运动的卫星轨道的示意图，其半径为R，曲线Ⅱ是一颗绕地球做椭圆运动的卫星轨道的示意图，O点为地球球心，AB为椭圆的长轴，两轨道和地心都在同一平面内，已知在两轨道上运动的卫星的周期相等，万有引力常量为G，地球质量为M，下列说法错误的是A.椭圆轨道的半长轴长度为RB.卫星在I轨道的速率为υ0，卫星在Ⅱ轨道B点的速率为υB，则υ0>υBC.卫星在I轨道的加速度大小为a0，卫星在Ⅱ轨道A点加速度大小为a A，则a0<a AD.若OA=0.5R，则卫星在B点的速率υB 23 GM R16.水刀切割具有精度高、无热变形、无毛刺、无需二次加工以及节约材料等特点，得到广泛应用。

某水刀切割机床如图所示，若横截面直径为d 的水流以速度v垂直射到要切割的钢板上，碰到钢板后水的速度减为零，已知水的密度为ρ，则钢板受到水的冲力大小为A．πρd2v B．πρd2v2C．14πρd2v2D．14πρd2v17.如图所示，木箱通过轻绳Ob悬挂在天花板下，木箱内有一竖直轻弹簧，弹簧上方有一物块P，竖直轻绳Pc上端与木箱相连，下端与物块P相连，系统处于静止状态。