单排双级行星轮运动特性方程式的推演
- 格式:doc
- 大小:104.50 KB
- 文档页数:3






单排单行星齿轮机构一般运动规律方程式1. 引言1.1 概述在现代机械领域中,齿轮传动作为一种常见的传动方式,被广泛应用于各种机械装置和设备中。
单排单行星齿轮机构作为其中的一类特殊结构,在其简洁紧凑的设计和高效率的工作原理下取得了广泛关注。
本文将深入研究单排单行星齿轮机构的运动规律方程式,以揭示其运转过程中的内部性质与特点。
1.2 文章结构本文共分为五个主要部分。
引言部分(第1节)简要介绍了撰写这篇长文的背景,并对文章所涉及内容进行了预览。
接下来是单排单行星齿轮机构的介绍(第2节),包括其定义和组成部分、工作原理以及应用领域。
之后是关键部分,即单排单行星齿轮机构的运动规律方程式(第3节),包括转速比计算公式推导、输入输出转矩计算方法以及齿轮传动效率分析与优化。
第4节将通过实例分析与研究结果展示来验证前面提到的方程式和方法的可行性,并介绍运动规律的仿真验证与实际应用案例。
最后,文章将在结论与进一步研究建议部分(第5节)总结研究结果并提出未来扩展研究的建议。
1.3 目的本文的目的在于通过深入研究单排单行星齿轮机构的运动规律方程式,揭示其内部传动特性和工作原理。
通过对转速比计算公式推导、输入输出转矩计算方法以及齿轮传动效率分析与优化等方面进行详细探讨,旨在为工程师提供一个全面且系统的了解和应用指南。
同时,本文还将通过实例分析与研究结果展示验证所提出的方程式和方法,并展示其在实际应用中的有效性和可行性。
最后,本文将总结当前研究结果,并提出进一步扩展研究方向的建议,以促进该领域未来更深入而宏观的发展。
2. 单排单行星齿轮机构的介绍2.1 定义和组成部分单排单行星齿轮机构是一种常见的传动装置,由一个太阳齿轮、多个行星齿轮和一个内六角环齿轮组成。
其中,太阳齿轮位于中心,行星齿轮与太阳齿轮相互啮合,并通过内六角环齿轮将力传递到外部。
2.2 工作原理在单排单行星齿轮机构中,太阳齿轮为输入端,通过其旋转驱动行星齿轮运动。


高中物理专题6.1行星的运动讲基础版含解析新人教版必修26、1 行星的运动※知识点一、两种对立的学说内容局限性地心说地球是宇宙的中心,而且是静止不动的,太阳、月亮以及其他行星都绕地球运动都把天体的运动看得很神圣,认为天体的运动必然是最完美、最和谐的匀速圆周运动,但计算所得的数据和丹麦天文学家第谷的观测数据不符日心说太阳是宇宙的中心,而且是静止不动的,地球和其他行星都绕太阳运动※知识点二、开普勒行星运动定律定律内容公式或图示开普勒第一定律所有行星绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上开普勒第二定律从太阳到行星的连线在相等的时间内扫过相等的面积开普勒第三定律所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等公式:,k是一个与行星无关的常量★1、开普勒第一定律说明了不同行星绕太阳运行时的椭圆轨道是不同的。
2、开普勒第二定律说明了行星在近日点的速率大于在远日点的速率。
3、开普勒第三定律(1)表达式=k,其中a是椭圆轨道的半长轴,T为公转周期,k是与太阳质量有关而与行星无关的常量。
(2)行星的椭圆轨道都很接近圆。
在近似的计算中,可以认为行星以太阳为圆心做匀速圆周运动。
若用r代表轨道半径,T代表周期,开普勒第三定律可以写成=k。
(3)开普勒定律不仅适用于行星,也适用于卫星,此时k是由行星的质量决定的。
★1、适用范围天体的运动可近似看成匀速圆周运动,开普勒第三定律既适用于做匀速圆周运动的天体,也适用于做椭圆运动的天体。
2、用途(1)知道了行星到太阳的距离,就可以由开普勒第三定律计算或比较行星绕太阳运行的周期。
反之,知道了行星的周期,也可以计算或比较其到太阳的距离。
(2)知道了彗星的周期,就可以由开普勒第三定律计算彗星轨道的半长轴长度,反之,知道了彗星的半长轴也可以求出彗星的周期。
3、k值:表达式=k中的常数k,只与中心天体的质量有关,如研究行星绕太阳运动时,常数k只与太阳的质量有关,研究卫星绕地球运动时,常数k只与地球的质量有关。


再谈行星齿轮机构的运动规律专家会诊————一——编者按:本刊2006年第10期刊登了————一——————————~————,曹利民老师的《丰田A761/A760自动变速器动力传递路线分析》一文后,收到了一些读者的来电或来信,指出文中给出了单级行星齿轮机构和双级行星齿轮机构的运动规律,但其中对双级行星齿轮的运动规律(见表1)与某知名专家编写的教材中给出的运动规律(见表2)有所不同,不知哪个是正确的.也有的读者说,自己已经动手转动双级行星齿轮机构,实际的运动规律与曹利民老师给出的结论一致,但不知这一结论的理论依据是什么.本刊将这些读者反馈转交给了曹利民老师,这是他给出的答复.表1双级行星齿轮机构的运动规律(本刊)表2双级行星齿轮机构的运i由规律(其他教材)■谨.|l彰J1l-l≥J1一一叠一啊目■I=_i一1太阳齿轮行星齿轮架内齿圈1一增速反向1减速同向仑行星架齿圈减速同向2行星齿轮架太阳齿轮内齿圈1一1宅齿圈行星架增速同向3行星齿轮架内齿圈太阳齿轮减速同向一14内齿圈行星齿轮架太阳齿轮1一!增速同向行星架太阳轮不确定l'x.1-J5太阳齿轮内齿圈行星齿轮架减速同向1太阳轮行星架不确定厦l口J6内齿圈太阳齿轮行星齿轮架增速同向程齿圈太阳轮增速同向7任两原件连成一体1直接传动襄太阳轮齿圈减速同向即无任一元件锁定又无任二元件连成一体三元件不传递动力自由转动再谈行星齿轮栅构的运动规律读者朋友,大家好:你们的反馈转交给我后,有些已给了回复,有些还没有回复,因人数较多,在这里一并回复.我们已熟悉了定轴轮系中齿轮啮合的运动规律,◆图2614T45E60汽车维修技师◆图262(待续)比如齿轮的外啮合改变旋转方向;齿轮的内啮合不改变旋转方向;多级齿轮啮合的传动比只与最初级和最末端齿轮的齿数有关系,与中间轮的多少及轮的齿数没有关系等等.在行星齿轮机构中,如果行星架固定,还可以按定轴轮系齿轮啮合的运动规律和传动比计算方法来推断;如果行星架不固定,则行星齿轮在自转的同时,还随着行星架的转动而公转,这使得定轴轮系的运动规律及传动比的计算方法有所不同.行星齿轮机构的运动规律分析的基础是定轴轮系,双级行星齿轮机构运动规律的分析基础是单级行星齿轮机构,下面先看一下单级行星齿轮机构的运动规律.最简单的行星齿轮机构由一个太阳轮,一个内齿圈和一个行星架组成,我们称之为一个单排单级行星排,如图1所示.由于行星齿轮机构具有两个自由度,为了获得固定的传动比,需将太阳轮,齿圈或行星架三者之一制动(转速为o)或约束(以某一固定的转速旋转),以获得我们所需的传动比如果将三者中的任何两/t-连接为一体,则整个行星齿轮机构以同一速度旋转.1.太阳轮2.行星轮3.内齿lI4.行星架!虽皇壁堡垦堂整塑行星齿轮机构的运动规律包括旋转方向和传动比两个重要指标,目前,在自动变速器的资料中,有关传动比的计算公式有以下几个:(nl—nH)/(n3一nH)=--Z3/Zl式(1)式中:n.一太阳轮转速n一行星架转速n一内齿圈转速Z.一太阳轮齿数Z一内齿圈齿数nl+o【n2一(1+o【)n3—0式(2)式中:n,一太阳轮转速n,一内齿圈转速n一行星架转速o【:内齿圈齿数/太阳轮齿数一Z,/Z.Z2一Z.+Z3式(3)式中:Z.一太阳轮齿数Z,一行星架假想齿数Z一内齿圈齿数下面对这3个公式的原理及推导过程作以介绍.上面提到的定轴轮系齿轮传动比计算公式为i一(一1)(所有的从动齿轮数乘积)/(所有的主动齿轮数乘积)一(一1)mZ/Z.,它对行星齿轮机构是不适用的.因为在行星齿轮机构中,星轮在自转的同时,还随着行星架的转动而公转,这使得定轴轮系传动比的计算方法不再适用.我们可以用"相对速度法"或"转化机构法"对行星齿轮机构的传动比进行分析,这一方法的理论依据是"一个机构整体的绝对运动并不影响其内部各构件间的相对运动",这就好像手表表针的相对运动并不随着人的行走而变化一样,这一理论是一位名叫Willes的科学家于1841年提出的.假定给整个行星轮系加上一个绕中心点旋转的运动(一),这个运动的角速度与行星架转动的角速度(co)相同,但方向相反,这时行星架静止不动,使星轮的几何轴线固定,我们就得到了一个定轴轮系,这样就能用定轴轮系的方法进行计算了. 用转速n代替角速度co,不同构件转化前和转化后的转速见表3.表3不同构件转化前和转化后的转速■■■■■…-_______.■■■■一?l____一1太阳轮n.=n1一nH2内齿圈n3:n3一nH3行星架nH:H=0利用定轴轮系传动比计算公式有:iHl3一nH1/n3一(n1一nH)/(n3--rlH)一(一1)Z2Z3/Z.Z2~Z3/z.式(4)如果把13(一Z,/Z.代入式(2)中,可得到式(1)或式(4).由此可见,这3个公式其实是同一个公式的不同表达方式.但需注意:这些公式只适用于单级的行星齿轮机构.在式(4)中,假设固定内齿圈,使n:0,代入式(4)得式(5):nl/nH一(Zl+Z3)/Zl式(5)又:I'lH—nl/nH=ZH/Zl式(6)联解式(5),(6)可得出:ZH—Zl+Z3即"行星架的假想齿数是太阳轮齿数和内齿圈齿数之和".注意,这一结论只适用于单级行星齿轮机构,在双级行星齿轮系就不适用了.下面对单极行星齿轮机构运动状态进行分析.1.太阳轮固定(n.一0),行星架驱动,内齿圈输出:将n10代入式(4),有i=nH/n3一z3/(z.+z),传动比小于1,即为同向增速运动.2.太阳轮固定(n,一0),内齿圈驱动,行星架输出:将rl10代入式(4),有i=n3/nH:(Z.+Z3)/Z3,传汽车维修技师61■■■I诊会家专动比大于l,即为同向减速运动.3.齿圈固定(1q一0),行星架驱动,太阳轮输出:将n一0代入式(4),有i=nH/nl=zl/(zl+z3),传动比小于l,即为同向增速运动.4.齿圈固定(1q一0),太阳轮驱动,行星架输出:将n,一0代入式(4),有i=nl/nH一(zl+z3)/Zl,传动比大于l,即为同向减速运动.5.行星架固定(n一0),齿圈驱动,太阳轮输出:将n一0代入式(4),有i=n/n,=--Z,/Z,传动比小于l,且为负值,即为反向增速运动.6.行星架固定(n一0),太阳轮驱动,齿圈输出:将n一0代入式(4),有i=n./n=--Z/Z.,传动比大于l,且为负值,即为反向减速运动.根据以上分析,可得出单级行星齿轮机构的运动规律,见表4.表4单捧单级行墨齿轮机构的运动规律太阳轮行星架齿圈增速同向太阳轮齿■行星架减速同向齿圈行星架太阳轮增速同向齿一太阳轮行星架减速同向行星架齿圈太阳轮增速反向行星架太阳轮齿■髓反向双级行星齿轮机构示意图见图2,它与单排单级行星齿轮机构相比,多了一只啮合齿轮.◆图2双级行墨同样,根据转换法,对于多级啮合行星齿轮系,我们通过单排单级行星齿轮机构传动比的计算公式,可以推出如下公式:iHCK—nHG/nHK一(nG—nH)/(nK~nH)一(一1)m (从G到K所有的从动齿轮数乘积)/(从G到K所有的主动齿轮数乘积),(式中in为从G到K啮合齿轮的62汽车维修技师..对数)式(7)对于双级行星齿轮机构,m=2,从式(7)我们可以得出双级行星齿轮机构的运动方程式为:iHI3一nH1/nH3一(nl—nH)/(n3一nH)一(一1)z2Z3/ z,z,:z/z.式(8)上式也可以这样理解:因双级结构多了一级外啮合,故与单级相比传动比方向相反,式(4)中将原来的"一"号变为"+"号.在式(8)中,假设固定内齿圈.使n一0,代入式(8)得式(9):nl/n}{一(z3一z1)/Zl式(9)又:I'lH—nl/nH—zH/Zl式(10)IN解式(9),(10)可得出:ZH—Z3一Zl即双级行星齿轮机构中,行星架的假想齿数是内齿圈齿数减去太阳轮齿数.可见,双级行星齿轮机构的速比计算公式和行星架的假想齿数与单排单级行星齿轮机构是不同的.下面对双级行星齿轮机构运动状态进行分析:对于单排双级行星齿轮机构,有z>z,(z一Z.)<z,但(z一z.)与z.的大小比较不确定,所以在下面的旋转规律分析中,有些条件不具备的情况没有列出增速还是减速.1.太阳轮固定(n,一0),行星架驱动,内齿圈输出:将nl一0代入式(8),有i=nH/n3一z3/(z3一z1),传动比大于l且为正,即为同向减速运动.2.太阳轮固定(n,一0),内齿圈驱动,行星架输出:将nl一0代入式(8),有i=n,/n}{一(z3一z1)/Z3,传动比小于l且为正,即为同向增速运动.3.齿圈固定(n一0),行星架驱动,太阳轮输出:将n3—0代入式(8),有i=nH/nl=--Zl/(z3一z1),传动比为负,但是大于还是小于l不确定,故为反向运动. 4.齿圈固定(n一0),太阳轮驱动,行星架输出:将n3—0代入式(8),有i=nl/nH一一(z3一z1)/Zl,传动比为负,但是否大于或小于l不确定,故为反向运动. 5.行星架固定(n一0),齿圈驱动,太阳轮输出:将nH一0代入式(8),有i=n3/nl—z1/Z3,传动比小于l,且为正值,即为同向增速运动.6.行星架固定(n一0),太阳轮驱动,齿圈输出:将nH一0代入式(8),有i=nl/n3一z3/zl,传动比大于l,且为正值,即为同向减速运动.根据以上分析,将双级行星齿轮机构的运动规律列于表l,对于双级行星齿轮机构,有Z>z.,(z一Z.)<z,但(z一z.)与Z.的大小比较不确定,所以在表1的旋转规律中,有些条件不具备的情况没-N~ll出增速还是减速.以上结论经过笔者在修理实践和教学过程中多次验证.田W渗¨会凉专■■■■■。
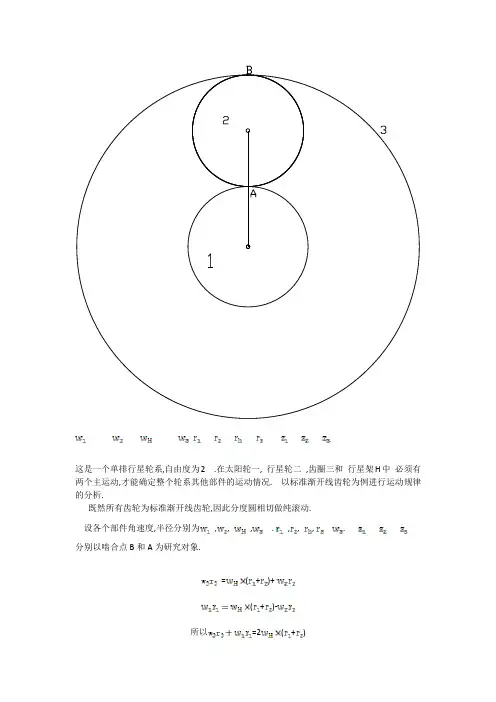
这是一个单排行星轮系,自由度为2 .在太阳轮一, 行星轮二,齿圈三和行星架H中必须有两个主运动,才能确定整个轮系其他部件的运动情况. 以标准渐开线齿轮为例进行运动规律的分析.
既然所有齿轮为标准渐开线齿轮,因此分度圆相切做纯滚动.
设各个部件角速度,半径分别为,, ,.,, ,.
分别以啮合点B和A为研究对象.
=(+)+
(+)-
所以=2(+)
如上图,显然: =(-)/2
所以: = 2(+(-)/2) = (+)
所以=(+)
标准渐开线齿轮r=mz 模数m都相等.所以
=(+)
这里,为太阳轮齿数,为齿圈齿数。
不管齿圈以及三个齿轮中哪两个是主动输入的运动。
两个啮合点上两部件速度相等是一定的。
因此不管单排还是多排行星轮系。
同一排的行星轮系中这几个部件的角速度必然符合此规律。
单排双级行星齿轮机构运动规律1. 引言嘿,朋友们,今天咱们聊聊一个听起来挺高大上的话题——单排双级行星齿轮机构。
哎,别一听这名字就觉得头大,咱们慢慢说,绝对让你听得明明白白。
说实话,这东西就像个“齿轮大家族”,在机械界里可有着举足轻重的地位呢!咱们不妨把它比作一个大家庭,里面的成员各司其职,团结协作,没它可真不行。
2. 什么是单排双级行星齿轮机构?2.1 基本构造首先,咱得了解一下这玩意的基本构造。
单排双级行星齿轮机构通常包括一个中心的“太阳齿轮”,周围围着几个“小行星齿轮”,它们就像小孩子围着爸爸转圈圈一样,真是萌萌哒!而这些小行星齿轮又通过一个“环齿轮”把整个结构给包裹起来,形成一个紧密的小圈子。
这样的设计让它在转动的时候,动力传递既顺畅又稳定,就像是开车时的顺风耳,声音嘹亮、稳当!2.2 工作原理说到它的工作原理,就更有趣了。
这种机构的妙处在于,它能同时实现多个传动比。
通俗点说,就是在不同的“档位”下,轻松调节转速和扭矩。
你想啊,开车时你有一档、二档,甚至是倒档,这个机构就是在给你一种“随心所欲”的体验。
无论是低速高扭矩,还是高速低扭矩,它都能应对自如,真是个“全能选手”。
3. 单排双级行星齿轮的运动规律3.1 运动特性那么,这个单排双级行星齿轮机构的运动规律又是怎样的呢?它在转动过程中,各个齿轮之间的相对运动关系可谓是微妙无比。
比如说,当太阳齿轮转动时,小行星齿轮也会跟着转动,嘿,没错,就是“一个带着一个走”。
这就像是传球游戏,你传我,我传你,转动的节奏感恰到好处,让整个机构在相互配合中,达成一种完美的和谐。
3.2 力学分析从力学的角度来看,这个机构的运动规律就更有意思了。
由于小行星齿轮在环齿轮和太阳齿轮之间不断地“转圈”,它们的受力情况也千变万化。
这种力的传递就像是“风吹草动”,一丝微小的变化都能影响整个机构的运行效率。
因此,在设计时,工程师们得仔细计算每一个参数,确保它在各种工况下都能稳定工作,就像是在调试一台高端音响,得听出每个音符的细微变化,才能把美妙的旋律演绎得淋漓尽致。
1
单排双级行星轮运动特性方程式的推演
李书江
1单排双级行星轮系的结构,如图所示。
下图为受力图,其中R 1、R 2、R 3、R 4分别为太阳轮、齿圈及两个行星轮的节度圆半径;F 1、F 2、F 3、F 4、F 5分别是太阳轮、齿圈、两行星轮及行星架相互之间的作用力;A 是太阳轮、齿圈和行星架的运动中心;B 、C 分别为两个行星轮的自转中心。
2单排双级行星轮系运动特性方程式的推导
2.1分析行星轮B 的平衡
(1)根据行星轮力矩平衡条件,有:
3133R F R F ⨯=⨯,即,F 1=F 3
(2)根据行星轮力的平衡条件,有:
0431=++F F F
故,在⊥AB 方向的分力有:
2 F 41=F 1+F 3cos a ,即,F 41=F 1(1+cos a )
2.2分析行星轮C 的平衡
(1)根据行星轮力矩平衡条件,有:
43342R F R F ⨯=⨯,即,F 2=F 33
由于,F 1=F 3,F 33=F 3(作用力与反作用力) 故,
F 2= F 1 ,F 33= F 1
(2)根据行星轮力的平衡条件,有: 03352=++F F F
故,在⊥AC 方向的分力有:
F 51=F 2+F 33cos b ,即,F 51= F 1(1+cos b )
2.3 求解三元件转矩
令三元件中太阳轮、齿圈及行星架的转矩分别为M 1、M 2、M 3,则:
M 1=F 1×R 1 ;
M 2 = -F 2×R 2= -F 1×R 2 ;
M 3= F 51(R 2-R 4) -F 41(R 1+R 3)
= F 1(1+cos b )(R 2-R 4)-F 1(1+cos a )(R 1+R 3)
2.4有关尺寸关系
(1)由图.2不难看出,
∠b=∠c ;∠a=∠d=180°-∠f
(2)在三角形△ABC 中,根据余弦定理得:
)
)(()()()(cos cos 4243231242243R R R R R R R R R R c b -++--++== ))(()()()(cos )180cos(cos 31432
43231242R R R R R R R R R R f
f a o +++-+--=-=-=
2.5功率守恒
根据能量守恒定律,太阳轮、行星架及齿圈三元件的输入和输出功率相等,即三者功率代数和为零,即:
M 1×n 1+M 2×n 2+M 3×n 3=0
式中n 1、n 2、n 3分别为太阳轮、齿圈、行星架
转动角速度。
将2.2.3的M 1、M 2、M 3以及2.2.4中的cosa 、cosb 代入上式,整理得:
n 1×R 1+ n 3×(R 2﹣R 1) = n 2×R 2-------(1)
3单排双级行星轮系运动特性应用式
3.1齿轮传递关系
由齿轮传递原理可知,模数相同的齿轮才能配对使用。
因此,单排行星轮系相啮合各齿轮的模数均相同。
若太阳轮和齿圈的齿数分别为Z 1、Z 2,那么:
2 R 1 = m ×Z 1 2 R 2 = m ×Z 2
3.2运动特性方程应用式
将3.1中的两式代入(1),得出单排双级行星轮系运动特性应用式:
n 1 Z 1+ n 3( Z 2 -Z 1)= n 2 Z 2
3。