当前位置：文档之家 › 第6章 控制系统的频域分析与设计65 奈氏图分析PPT课件

第6章 控制系统的频域分析与设计65 奈氏图分析PPT课件

  • 格式：ppt
  • 大小：637.50 KB
  • 文档页数：30

下载文档原格式

  / 30

合集下载

控制工程基础课件第六章 频率特性分析

控制工程基础课件第六章 频率特性分析


G
j
arctan
1
n 2
n2
当=0时，G j 1，G j 0；
当=n时，G j 2，G j 90； 当=时，G j ，G j 180。
二阶微分环节的极坐标图也于阻尼比有关，对应不同的 ξ值，形成一簇坐标曲线，不论ξ值如何，当ω=0时，极 坐标曲线从(1,0)点开始，在ω=∞时指向无穷远处。
第6章 频率特性分析
本章介绍线性系统的频域分析方法。该方法是通 过控制系统对正弦函数的稳态响应来分析系统性能的。
频率特性不仅能反映系统的稳态性能，也可用来 研究系统的稳定性和动态性能。
6.2 频率响应与频率特性
一、频率特性的概念
1、频率响应：是系统对正弦输入的稳态响应。
2、频率特性：给线性系统输入某一频率的正弦波，
1 1 jT
G j 1 U jV
1 jT
1
1 T 22
j T 1 T 22
A e j
实频特性为U 虚频特性为V
1； 1+T 2 2
T。 1+T 2 2
幅频特性为A 1 ；
1 T 22
相频特性为 G j arctanT
特殊点：
当=0时，G j 1，G j 0； 当=1/T时，G j 1 ,G j 45；
取拉氏变换为： Xi s
A
s2
2
电路的输出为： X0 s G s Xi s 上式取拉氏反变换并整理得
1A Ts 1 s2 2
x0 t
AT 1 T2
e t/T
2
A sin t arctan T
1 T2 2
x0 t
AT 1 T2
e t/T
2
A sin t arctan T
自动控制原理课件：线性系统的频域分析

自动控制原理课件：线性系统的频域分析

曲线顺时针方向移动一周时，在 平面上的映射曲线按逆时针方向
包围坐标原点 − 周。
m
F (s)
K1 ( s z j )
j 1
n

i 1
( s pi )
24
• 02
基本概念
m
1 G ( s) H ( s) F ( s)
K1 ( s z j )
j 1
在 平面上的映射曲线 F 1 G ( j ) H ( j )将按逆时针方向
围绕坐标原点旋转 = − 周。
如果在s平面上，s沿着奈奎斯特回线顺时针方向移动一周时，
在 平面上的映射曲线围绕坐标原点按逆时针方向旋转 =
周，则系统为稳定的。
26
根据
( 1, j 0)
L( ) 20 lg K 20 lg 1 12 2 20 lg 1 22 2
( ) arctg 1 arctg 2
τ2
20dB / dec 1
2

L3 ( )
L2 ( )
40dB / dec
( )
0
L( )

90
A( ) 1, ( )
L ( ) 20 lg A( ) 0
L( )
jQ( )
L( ) 0
0
( )
1
0
1
P( )
1

0


30

60
16
5.3
系统开环频率特性图
设开环系统由n个典型环节串联组成
G(s ) G 1(s )G 2(s ) G n(s )
这意味着 的映射曲线 F 围绕原点运动的情况，相当于
自动控制理论 线性系统的频域分析法

自动控制理论 线性系统的频域分析法

A() P2 () Q2 ()
() tg 1 Q() P( )
线性系统的频域分析法>>线性系统的频域特性
频率特性与传递函数的关系为：
G( j ) G(s) |s j
由于这种简单关系的存在，频率响应法和利用传递函数的时域 法在数学上是等价的。
[结论]：当传递函数中的复变量s用 j代替时，传递函数就转变
第六章 线性系统的频域分析法
1 线性系统的频率特性及图示 2 开环系统的典型环节 3 频率域稳定判据 4 稳定裕度 5 闭环系统的频域特性
线性系统的频域分析法>>线性系统的频域特性
6.1 频率特性的基本概念
考察一个系统的好坏，通常用阶跃输入下系统的阶跃响应 来分析系统的动态性能和稳态性能。
有时也用正弦波输入时系统的响应来分析，但这种响应并 不是单看某一个频率正弦波输入时的瞬态响应，而是考察频率 由低到高无数个正弦波输入下所对应的每个输出的稳态响应。 因此，这种响应也叫频率响应。
N (s)
Rm
(s p1)(s p2 )...(s pn ) (s p1)(s p2 )...(s pn ) (s j )(s j )
k1 k2 ... kn kc1 kc2
s p1 s p2
s pn s j s j
拉氏反变换为：
c(t) k1e p1t k2e p2t ... kne pnt kc1e jt kc2e jt
频率响应法的优点之二在于它可以用图来表示，这在控制 系统的分析和设计中有非常重要的作用。
由实验方法求频率特性
正弦信号 发生器
实验装置 （系统或元件）
双踪 示波器
图 求频率特性的实验方法
系统的幅频特性： | G( j) | Y
系统的频域分析方法ppt课件

系统的频域分析方法ppt课件


此法与§1.8的算子电路法相似，利用频域电路简化运算。
动态元件时域与频域电压电流关系表示为
vL t
L
d dt
iL
t


VL


jL IL
vC
t


1 C
t
iC பைடு நூலகம் d
VC
1 jC
IC

上两式中 jL 为频域的感抗值，是电感的频域表示； 1 为频域的容抗值，是电容的频域表示；两个等式

jC
将(1)式代入(2)式
15
Y j
1/ jC
F j
R jL 1/ jC
得系统频响函数
H j
Y j F j

R

1/ jC jL 1/
jC


j2
LC
1
jRC
1
16
2、系统的频域分析 由卷积定理我们可以得到频域分析法的基本方框图表示，
如图2-29所示。
f t
F j
h t
H j
yzs t f t ht
Y j F jH j
例 2-16
已知系统函数
H j
j 3
j 1 j 2
，激励
f t e3tut 。求响应。
17
例 2-16
已知系统函数
H j
j 3
j 1 j 2
，激励
f t e3tut 。求响应。
解
yt Y j F jH j
Y

j


j

1
1
控制系统频域分析

控制系统频域分析


c •
K g 0 系统不稳定
在Bode图上可测取相角裕度和幅值裕度
L() dB
1
kg
20 lg h
20 lg
| Gk ( jg ) |
0dB
c
kg rad / s
20 lg | Gk ( jg ) |
F( )
00
-1800
g
rad / s
MATLAB中用来求系统幅值裕度和相位裕度的函数为 margin( )，它的调用格式有以下几种：
1
| Gk ( jg ) |
例：已知系统开环传递函数为：
Gk
s
ss
5
10.1s
1
试绘制系统Bode图并求系统相角裕量和幅值裕量。
num=[5]; den=conv (conv ([1 0],[1 1]), [0.1 1]); sys=tf (num, den); margin (sys) [Gm,Pm,Wg,Wc]=margin (sys)
系统的频域性能指标为：
Gm =2.2000；Pm =13.5709；Wg =3.1623；Wc = 2.1020
即：系统的剪切频率ωc=2.1020rad/s；相位裕度 =13.5709°，
相位穿越频率ωg=3.1623rad/s； 幅值裕量kg=20*log10(2.2)=6.8485dB。
一、极坐标图（Nyquist图） 当ω：0→∞变化时，G(jω)的端点在复平面上的运动轨迹。
注意：极坐标图中ω是隐含变量。在作图时要注明ω= 0， 和ω→∞的位置及运动轨迹的方向。
MATLAB中用来绘制连续系统极坐标图的指令为 nyquist( )，其调用格式为：
nyquist (sys)——sys为由tf、zpk建立起来的控制系统数 学模型。此时绘制出来的极坐标图的默认角频率w是从 -∞~ +∞。这点与自动控制原理略有不同。
控制系统的频域分析29页PPT

控制系统的频域分析29页PPT

42、只有在人群中间，才能认识自 己。——德国
43、重复别人所说的话，只需要教育； 而要挑战别人所说的话，则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是：在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联

控制系统的频域分析
51、山气日夕佳，飞鸟相与还。 52、木欣欣以向荣，泉涓涓而始流。
53、富贵非吾愿，帝乡不可期。 54、雄发指危冠，猛气冲长缨。 55、土地平旷，屋舍俨然，有良田美 池桑竹 之属， 阡陌交 通，鸡 犬相闻 。
41、学问是异常珍贵的东西，从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
控制系统频域课件-奈氏判据

控制系统频域课件-奈氏判据

第4章
控制系统频域分析法
1
第4章 频域分析法
基本要求
4－1 频率特性 4－2 典型环节的频率特性 4－3 系统的开环频率特性 4－4 频率稳定判据 4－5 系统闭环频率特性与阶跃响应的关系 4－6 开环频率特性与系统阶跃响应的关系
2
系统的开环频率特性-Nyquist图

一、开环幅相特性曲线 设系统开环传递函数由若干典型环节串联
对数图上 ( ) 180 时的 L ( g )
K g ( dB ) 0 系统稳定（对最小相位系统）
180 G ( j c ) H ( j c )
25
相稳定裕度和模稳定裕度
26
一般要求
pm 4 0

h 2
2 0 lo g h 6 d B
6
（3）当
G s K s Ts 1

时，
开环传递函数有 积分环节时，频 率趋于零时，幅 值趋于无穷大。
含有积分环节时的开环 幅相特性曲线
7
2.系统开环幅相的特点
①
当频率 ω → 0 时，其开环幅相特性完 全由比例环节和积分环节决定。 当频率ω→∞ 时，若n>m，G(j ω)|=0 相角为(m-n)π/2。 若G(s) 中分子含有s因子环节，其G(jω) 曲线随 ω变化时发生弯曲。 G(jω) 曲线与负实轴的交点，是一个关 键点。 8
幅相曲线（a)及对应的对数频率特性曲线(b)
17
系统闭环稳定的条件是：
在开环对数幅频 2 0 lg G ( j ) 0 的频段内，对应的开 环对数相频特性曲线对 线的正、负穿越次数之 差为 P / 2 。即
N N P / 2
控制系统的频域分析与设计65奈氏图分析

控制系统的频域分析与设计65奈氏图分析

的次数N等于位于右半平面上开环极点数P。则闭 环系统稳定，否则闭环系统不稳定。 约束条件：在原点和虚轴上无零极点。奈氏轨迹不 能穿过零极点。 讨论：当奈氏曲线通过,j0点，则表示闭环系统 临界稳定，也归为不稳定。
第9页/共79页
应用奈氏稳定性判据一的步骤：
绘G( j)H ( j) 的奈氏图，可先绘 :一段，
=0
-1
=-
=+
第11页/共79页
三. 奈氏稳定性判据二
若增补奈氏曲线 G( j)H ( j)当:逆时针
包围, j0点的次数N等于位于右半平面上开环极点 数P。则闭环系统稳定，否则闭环系统不稳定。
所谓增补就是使奈氏轨迹绕开位于原点和虚轴上 的开环零极点。
增补奈氏轨迹：
第12页/共79页
增补奈氏轨迹映射出的奈氏轨迹分析：
解：作奈氏曲线考虑增补
当:顺时针 包围,j0点2次， N=2 P=0 Z=2 不稳定
=- =
• (-1,j0)
=
第16页/共79页
GH平面
例：G(s)H (s) (s 0.2)(s 0.3) s2 (s 0.1)(s 1)(s 2)
试判定闭环系统稳定性
解：作增补奈氏曲线
N=0，不包围, j0点
PiII，i P 1， ，n ZiII，i Z 1， ，m
对于任一点s有F平面映射
Z
m
K
(s
Z
I i
)
(sΒιβλιοθήκη ZII i)
F(s)
i 1 P
iZ 1 n
(s PiI ) (s PiII )
i 1
i P 1
第4页/共79页
Z
m
F(s)
(s
第六章 控制系统的频率特性

第六章 控制系统的频率特性

第六章 控制系统的频率特性采用频率特性法原因： （1） （2） （3）第一节 频率特性的基本概念一．概念 1．频率响应：指控制系统对正弦输入信号的稳态正弦输出响应。

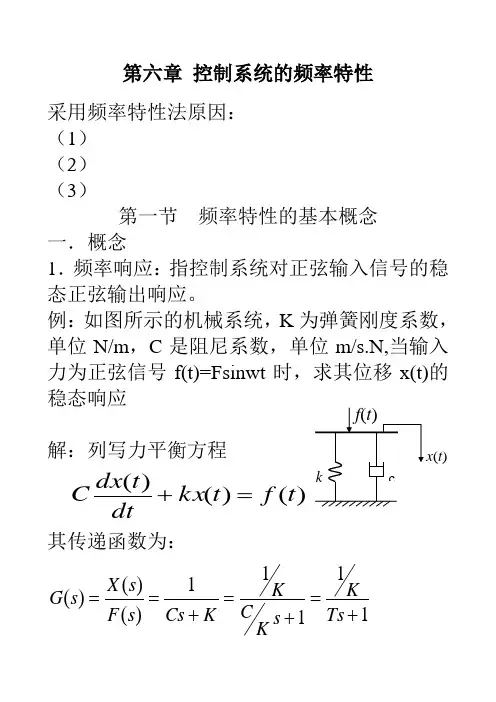
例：如图所示的机械系统，K 为弹簧刚度系数，单位N/m ，C 是阻尼系数，单位m/s.N,当输入力为正弦信号f(t)=Fsinwt 时，求其位移x(t)的稳态响应解：列写力平衡方程)()()(t f t kx dtt dx C =+其传递函数为：11111)()()(+=+=+==Ts K s KC K K Cs s F s X s Gx (t )tF t f ωsin )(=22)(ωω+=s F s F输出位移)()()(s F s G s X =2232122111ωωω++++=+⋅+=s K s K Ts k s F s KCKTt e T KF T T arctg t T K Ft x -++-+=22221)sin(1)(ωωωωω上式中第一项为稳态分量，第二项为瞬态分量，当时间t 趋向于无穷大时为零。

系统稳态输出为：)](sin[)](sin[)()sin(1)(22ωϕωωϕωωωωω+=+⋅=-+=t X t F A T arctg t T K Ft x其幅值为：2)(11)()(ωωωT K F X A FA X +===相位为：T arctg ωωϕ-=)(从上式的推导可以看出，频率响应是时间响应的一种特例。

正弦输入引起的稳态输出是频率相同的正弦信号，输入输出幅值成比例)(ωA ，相位)(ωϕ都是频率ω的函数，而且与系统的参数c,k 有关。

二 频率特性及其求解方法 1．频率特性：指线性系统或环节在正弦函数作用下，稳态输出与输入幅值比)(ωA 和相位差)(ωϕ随输入频率的变化关系。

用)(ωj G 表示。

)()]([)(Im Im )()()(ωϕωωϕωωωj tj t j eA eF eX t f t x j G ===+2)(11)()(ωωωT K F X j G A +===T arctg j G ωωωϕ-=∠=)()()(ωj G 称为系统的频率特性，其模)(ωA 称为系统的幅频特性，相位差)(ωϕ称为相频特性2．频率特性求解 （1）根据已知系统的微分方程或传递函数，输入用正弦函数代入，求其稳态解，取输出和输入的复数比（2）根据传递函数来求取 （3）通过实验测得令传递函数中的ωj s =则得到频率表达式)(ωj G ，又由于)(ωj G 是一个复变函数，可在复平面上用复数表示，分解为实部和虚部，即：)()()()()(w j e w A w jV w U jw G ϕ=+=)(cos )()(w w A w U ϕ= )(sin )()(w w A w V ϕ=)()()(22w V w U w A += )()()(w U w V arctg w =ϕ例：某闭环系统传递函数为237)(+=s s G ，当输入为)4532sin(71 +t 时，试求系统稳态输出。

控制系统频域设计示范教学课件

控制系统频域设计示范教学课件


06
控制系统频域设计实验指导
实验目的与要求
掌握频域分析方法在控制 系统设计中的应用。
培养学生对控制系统的理 解和设计能力。
学会利用频域法分析系统 的稳定性、快速性和准确 性。
实验设备与器材
计算机（配备MATLAB软 件）
控制系统实验箱
信号发生器
示波器
数据采集卡
实验步骤与操作
进行频域分析，计算系统 的频率响应。
频域设计与时域设计的关系
01
时域设计和频域设计是控制系统设计的两种基本方法，它们分别从不同的角度 描述系统的性能。
02
时域设计关注系统在时间域中的动态行为，而频域设计关注系统在频率域中的 性能表现。
03
在实际设计中，时域设计和频域设计常常是相互补充的。时域设计方法可以提 供关于系统动态特性的直观理解，而频域设计方法可以提供关于系统稳定性和 性能的全面描述。
分析方法
通过判断系统的极点和零点位置，以及它们的实部和 虚部来判断系统的稳定性。
重要性
稳定性是控制系统设计的首要考虑因素，不稳定的系 统无法正常工作。
性能指标分析
01 定义
性能指标是用来评估控制系统性能好坏的一系列 参数。
02 分析方法
通过频率响应函数计算出系统的相角裕度、幅值 裕度和穿越频率等性能指标，以评估系统的动态 性能和稳态性能。
02 通过调整系统参数，如增益和极点位置，可以改 善系统的性能。
闭环系统的频域设计
闭环系统的频域设计主要关注闭环系统的频率响 应，以实现特定的性能指标。
设计过程中，需要分析闭环系统的极点和零点分 布，以及它们对系统性能的影响。
通过调整闭环系统的极点和零点位置，可以优化 系统的性能，如提高稳定性和减小超调量。
控制系统的奈氏图分析自动控制原理理论篇第65节

控制系统的奈氏图分析自动控制原理理论篇第65节

, j0点转的圈数为N，（顺时针转取负值，逆时 针转取正值）当Z=P-N为零时，系统稳定；否则闭
环系统不稳定。
约束条件：在原点和虚轴上无零极点。奈氏轨迹不 能穿过零极点。
讨论：当奈氏曲线通过,j0点，则表示闭环系统 临界稳定，也归为不稳定。
例：G(s)H (s)
K (Tas 1)
N P Z,or Z P N
若N为正，则表示闭曲线C‘逆时针包围原点 的周数。 若N为负，则表示闭曲线C‘顺时针包围原点 的周数。 若N为零，则表示闭曲线C‘不包围原点转圈。 在N P Z 式中 Z——s平面上被封闭曲线C包围的Fs的零点 数 P——s平面上被封闭曲线C包围的Fs的极点 数 N ——F平面中封闭曲线C’包围原点的次数
G(s) 2 s 1
为例，求S平面上的点s0=1+j在G平面上的
映射。
解：
G(s) s1 j

1
2 j 1

0.8 0.4
j
b）线的映射
G(s) 2 ,求s -2j,0, j,2j在G(s)平面上的映射点. s 1
可看出将虚轴映射成圆.
2）映射定理 奈氏判据的理论基础是复变函数的映射定理。 定理：设F（S）：复变量S的单值解析函数， S平面 F（S）平面，它在S平面某一闭曲线C的内 部共有P个极点和Z个零点，且闭曲线C不通过F（S） 的任一极点和零点。当S顺时针方向沿闭曲线变化一 周时，函数F（S）所取值一随之连续变化而在F平面 上描出一个闭曲线C‘，曲线C‘称为C的映射。 在上述情形下闭曲线C‘包围原点的周数N为
一型系统的奈氏曲线
二型系统的奈氏曲线
（-M：900 -90） （-M：1800 -180）
=0-

控制系统的频域分析

第五章 控制系统的频域分析一、频域特性的概念线性定常系统在正弦输入信号的作用下，其输出的稳态分量是与输入信号相同频率的正弦函数。

输出稳态分量与输入正弦信号的复数比称为频率特性。

用数学式表示为：)()()(ωωωj X j Y j G = 系统的频率特性)(ωj G 是系统传递函数)(s G 的特殊形式，它们之间的关系是ωωj s s G j G ==)()(二、频率特性的表示方法直角坐标式： )()()(ωωωjI R j G += ，见图1.5-1式中：称之为实频特性-)(ωR称之为虚频特性-)(ωI极坐标式： )()()(ωφωωj e A j G = 式中：称之为幅频特性-=)()(ωωj G A称之为相频特性-∠=)()(ωωφj G 直角坐标和级坐标表示方法之间的关系是)()()()()()()(sin )()()(cos )()(122ωωωφωωωωφωωωφωωR I tg I R A A I A R -=+=== 图形如图1.5-1所示。

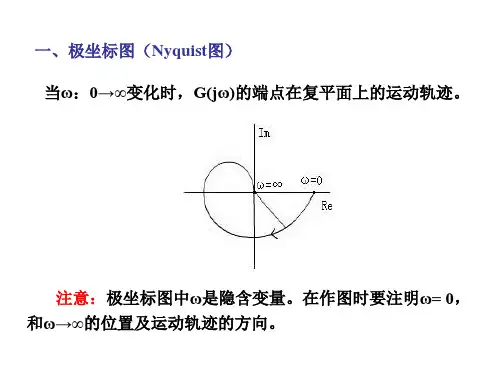
I 图1.5-1三、幅相频率特性曲线（又称乃氏图，乃氏曲线）以角频率ω为参变量，对某一频率ω，有相应的幅频特性)(ωA 和相频特性)(ωφ与之对应，当ω从∞→0变化时，频率特性构成的向量在复平面上描绘出的曲线称为幅相频率特性曲线。

又称为乃氏图、乃氏曲线。

四、对数频率特性（又称频率特性的对数坐标图，伯德图）对数频率特性图（伯德图）有两张图，一张为对数幅频特性曲线图，另一张是对数相频特性曲线图。

前者以频率ω为横坐标，并采用对数分度，将)(lg 20ωj G 的函数值作为纵坐标，并以分贝（dB ）为单位均匀分度。

后者的横坐标也以频率ω为横坐标（也用对数分度），纵坐标则为相角)(ωφ，单位为度)(︒，均匀分度。

两张图合起来称为伯德图。

五、奈奎斯特稳定性判据（又称奈氏判据）1. 对于开环稳定的系统，闭环系统稳定的充分必要条件是开环系统的奈氏曲线)()(ωωj H j G 不包围()0,1j -点。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

P i I ， I i P 1 ， ， n Z i I ， I i Z 1 ， ， m
对于任一点s有F平面映射
Z
m
K (sZiI ) (sZiII)
F(s)
i1 P
iZ1 n
(sPiI ) (sPiII)
i1
iP1
Z
m
F(s) (sZiI) (sZiII)
i1
iZ1
：上半虚轴映射为 ：下半虚轴映射为
右半圈映射为,，因为当 nm
F (s) 1 G (s)H (s) 1 s
回忆幅角原理 N=PZ，F的零点即闭环极点。
若要稳定，闭环极点应不在s右半平面。若以奈氏轨 迹为封闭曲线C，则它所包围的s右半平面零点数Z=0， 才有系统稳定，据幅角原理有Z=PN=0 （N为奈氏曲线 包围坐标原点的次数， P为奈氏轨迹包围的开环极点数）
P
n
(sPiI) (sPiII)
当变点s沿Ci1顺时针移动一i圈P1，则有
Z
m
F (s)
(
s
Z
I i
)
(s
Z
II i
)
i 1
iZ 1
P
n
(s PiI ) (s PiII )
i 1
i P1
Z (360 ) 0 P(360 ) 0
(360 )(Z P) 这表明F(s)端点沿C‘逆时针
若考虑G(j)H(j)平面，则相当于F( j)曲线左
移一个单位的奈氏图，即开环幅相频率特性，原F平面 原点对应于GH平面, j0点
G (j )H (j ) F (j ) 1
若要系统稳定，则Z=PN=0，N为GH 映射曲线绕 ,j0点次数
二. 奈氏稳定性判据一
若奈氏曲线 G(j)H(j)逆时针包围, j0点
-1
统计： N Ni Ni
例：G (s)H (s)s2((ss 0 0 .1 .2 ))s(s ( 1)0.s3 ( )2)
可见增补奈氏轨迹映射为半径的圆曲线变 点相角变化从M90 M90 如 M=1，
-M：90090
M=2时， -M：180 0 180
一型系统的奈氏曲线
二型系统的奈氏曲线
（-M：900 -90） （-M：1800 -180）
=-
=
= =
= GH平面
=- GH平面
例：设开环传函 G(s)H(s) 10 s(s1)s(2)
试用奈氏判据判定系统稳定性
解：作奈氏曲线考虑增补
当:顺时针 包围,j0点2次， N=2 P=0 Z=2 不稳定
=- =
• (-1,j0)
= GH平面
例：G (s)H (s)s2((ss 0 0 .1 .2 ))s(s ( 1)0.s3 ( )2)
试判定闭环系统稳定性
解：作增补奈氏曲线
N=0，不包围, j0点
环传函极点，若要闭环稳定，则Fs的全部零
点必须位于s左半平面。
2. 幅角原理 奈氏判据的理论基础是复变函数的幅角原理。应
用幅角原理可导出奈氏判据的重要公式：
NPZ
式中 Z——s平面上被封闭曲线C包围的Fs的零点数 P——s平面上被封闭曲线C包围的Fs的极点数 N ——F平面中封闭曲线C’包围原点的次数
例：G (s)H (s) K (T as1) (T 1s1)T (2s1)T (3s1)
解：作奈氏轨迹如下图示:
N=1， P=1 有Z=NP=0 故系统稳定
-1
=-
=0
=+
三. 奈氏稳定性判据二
若增补奈氏曲线 G(j)H(j)当:逆时针
包围, j0点的次数N等于位于右半平面上开环极点数 P。则闭环系统稳定，否则闭环系统不稳定。
的次数N等于位于右半平面上开环极点数P。则闭 环系统稳定，否则闭环系统不稳定。
约束条件：在原点和虚轴上无零极点。奈氏轨迹不 能穿过零极点。
讨论：当奈氏曲线通过,j0点，则表示闭环系统 临界稳定，也归为不稳定。
应用奈氏稳定性判据一的步骤：
绘G(j)H(j) 的奈氏图，可先绘 :一段，
再以实轴对称的方法添上:的一段； 计算奈氏曲线包围,j0点的次数N 由给定的Gss确定右半平面上开环极点数 P 计算 PN ，若 PN =0 则闭环稳定
2
1. 特征函数的零点和极点
特征函数—— F (s) 1 G (s)H (s)
对应的闭环系统
C(s) G(s) R(s) 1G(s)H(s)
F(s)0 即为闭环系统的特征方程。 n
若 GH B(s) A(s)
则 F(s)1B A((ss))Kni1(s(spzi)i)
推论： Fs的极点是开环传函极点；iF1s的零点是闭
360 (P Z ) 包围原点的次数为P-Z=N。
3. 奈氏轨迹及其映射
若选取适当的封闭曲将s平面右半平面包围起来，
则变点s顺时针方向沿虚轴和半径为的右半圈绕一周
形成的封闭曲线称为Nyquist轨迹 ，简称奈氏轨迹。
j
jI()
=±
•
=0 R()
S平面的奈氏轨迹
F(j)平面的奈氏曲线
奈氏轨迹在平面的映射也为一个封闭曲线， 称为 奈氏曲线, 例如
第五节 控制系统的奈氏图分析
一.奈氏判据的基本原理
奈氏判据——频域分析中最重要的稳定性判据。叙述 见后两节。 先讨论三个重要概念：
1. 特征函数的零点和极点 2. 幅角原理 3. 奈氏轨迹及其映射
第一部分
整体概述
THE FIRST PART OF THE OVERALL OVERVIEW, PLEASE SUMMARIZE THE CONTENT
j
C
s
(s+ZiII)
-ZiII -PiII
(s+ZiI)
-PiI -ZiI
s平面
jIm C’
F(s)
Re
F平面
证：设封闭曲线C不通过s平面上任一零极点，且包围
Z个零点P个极点，记为
P i I ， i 1 ， 2 ， ， P Z i I ， i 1 ， 2 ， ， Z
未被包围的零极点记为
=
P=0，Z=N-P=0
闭环稳定
=-
= • (-1,j0)
GH平面
补充：实用奈氏判据
若开环系统有q个 极点位于s右半平面，则当 :0时，穿越[段的次数N q ，则闭环稳
2 定，否则不稳定。（化数包围圈数为穿越次数）
穿越次数的计算按下定义：
半穿越
正穿越 负穿越
记法：
Ni
1 2
Ni
1 2
Ni 1 Ni 1
所谓增补就是使奈氏轨迹绕开位于原点和虚轴上 的开环零极点。
增补奈氏轨迹：
增补奈氏轨迹映射出的奈氏轨迹分析：
m
K(is 1)
G(s)H(s)
i1 nM
sM (Tis 1)
i1
当 se j (: 9 0 0 9)0
m
K (01)
G(s)H(s)MejM i 1nM(01)MK ejM ejM i1