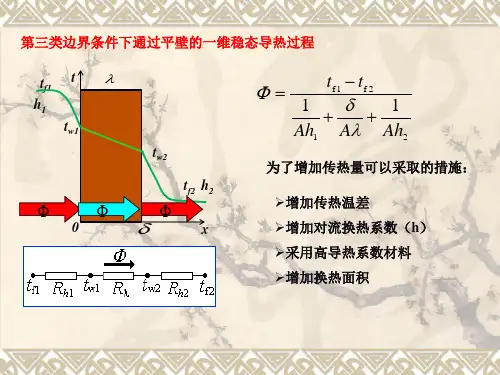
边界条件(B.C.): (1) y y0 , ux 0; (2) y y0 , dux dy 0 速度分布为
1 p 2 2 ux ( y y0 ) 2 μ x
抛物线形
当 y 0 时速度最大 1 p 2 umax y0 2 μ x
y 2 ux umax [1 ( ) ] y0
(1)非线性偏微分方程; (2)质点上的力平衡,仅能用于规则的层流求解。
动量传递变化方程的分析
变化方程组求解的分类:
(1)对于非常简单的层流,变化方程源自简化后, 其形式非常简单,可直接积分求解—解析解; (2)对于某些简单层流,可根据流动问题的物理 特征进行化简。简化后,积分求解—物理近似解; (3)对于复杂层流,可采用数值法求解;将变化 方程离散化,然后求差分解; (4)对于湍流,可先进行适当转换,再根据问题 的特点,结合实验,求半理论解。
动量传递变化方程的分析
动量传递变化方程组:
ρ ( ρu) + 0 θ
当流体不可压缩时,ρ=常数
Du 1 2 ρ ρf B p μ u μ( u) Dθ 3
u 0
Du ρ ρf B p μ 2 u Dθ
动量传递变化方程的分析
ux u y uz 0 x y z
2 u y 2 u y 2u y 1 p ux uy uz Y ν( 2 2 2 ) x y z θ ρ y x y z p ρY ρg y u y u y u y u y
一、变化方程的简化
2u x p μ( 2 ) x y p ρY ρg y p 0 z
( a) (b) (c)
(b)对 y 积分得
p( x, y) ρgy k ( x)