工程制图
基本体三视图
一. 基本概念
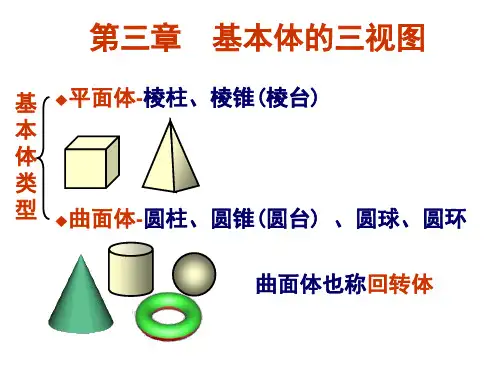
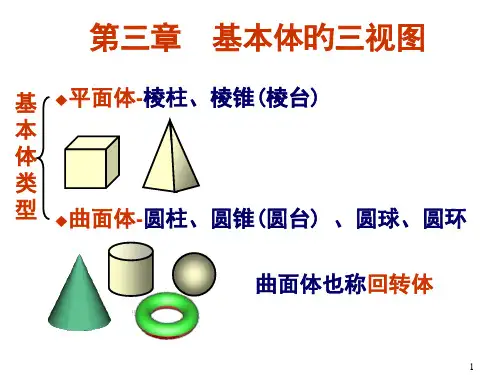
单一的几何体称为基本体. 单一的几何体称为基本体.如:棱 棱锥,圆柱,圆锥, 环等. 柱,棱锥,圆柱,圆锥,球,环等. 它们是构成形体的基本单元, 它们是构成形体的基本单元,在几何 造型中又称为基本体素. 造型中又称为基本体素. 基本体素
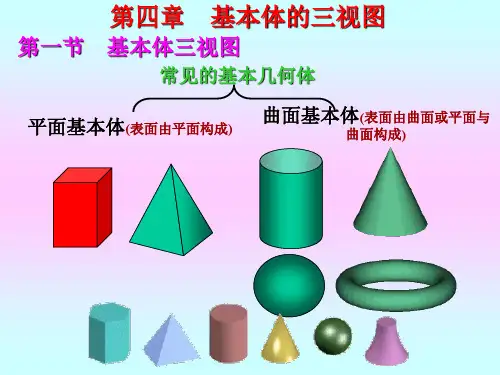
基本体的分类
常见的基本几何体 平面基本体 曲面基本体
S N M A B K C m' a' a m n b s k b' k' m" (k") c' a"(c") b" c s' n' s" n"
N∈ SB ∈ 注意分析点, 注意分析点,直线 K∈ SBC ∈ 所在表面的可见性 如何在平面上取点? 如何在平面上取点?
分析 M∈ SA 连线 ∈曲面体(回转体) 曲体(回转体) 圆柱体O
V
M
W
m'
( m" )
O
H
m
AC位于圆柱体表面 已知a 位于圆柱体表面, ac, 例 AC位于圆柱体表面,已知aΧcΧ,求ac, aΝcΝ
a' b' (c') d' c d a b 外形轮廓线上的 点是曲线投影的 虚,实分界点 (c'') (d'') a'' b''
分析
aΧcΧ不平行轴线 AC为曲线 故AC为曲线
S
s'
s"
V
W
H
对V面的外 对W面的外 形轮廓线 形轮廓线
s
外形轮廓线投 影的对应关系 圆锥面投影 可见性判断
圆锥体表面取点取线