matlab经典、现代功率谱估计
- 格式:pdf
- 大小:294.45 KB
- 文档页数:7
![基于Matlab实现现代功率谱估计[1]要点](https://uimg.taocdn.com/2b61a19e02d276a200292e77.webp)
2011年 8月 15日第 34卷第 16期现代电子技术M odern Electro nics T echniqueA ug. 2011V ol. 34N o. 16基于 Matlab 实现现代功率谱估计王春兴(山东师范大学物理与电子科学学院 , 山东济南 250014摘要 :功率谱估计可以分为经典谱估计和现代谱估计。
现代谱的估计可建立 A R 模型对离散信号进行谱估计、建立 M A 模型和 A RM A 模型进行谱估计。
基于 M atlab 对三种模型进行仿真 , 并对结果进行了分析。
结果显示 , 三种模型对现代谱的获得是有效的 , 并得到较好的谱估计。
关键词 :P SE; 现代功率谱估计 ; AR 模型法 ; A RM A中图分类号 :T N911-34; G202 文献标识码 :A 文章编号 :1004-373X (2011 16-0065-03Modern Power Spectrum Estimation Based on MatlabW AN G Chun -x ing(Colleg e o f Physics and Elect ro nics, Shando ng No rm al U niversity , Jinan 250014, Chi naAbstract :Po wer spectr um estimation can be divided into classical spectr al estimat ion and modern spectr al estimation. M odern spectr al estimation model can establish AR mo del, M A mo del and ARM A model fo r discr ete sig nals to per for m spec -t ralestimatio n. T hese t hr ee models can be simulated based o n M atlab, and the r esults ar e analy zed. T he r esult s sho w that the three models of mo der n spect rum are valid, and can get better spectrum estimatio n.Keywords :PSE; mo der n pow er spect rum est imatio n; A R model method; A RM A收稿日期 :2011-03-26基金项目 :国家自然科学基金项目资助 (10874103随机信号在时域上是无限长的 , 在测量样本上也是无穷多的 , 因此随机信号的能量是无限的 , 应用功率信号来描述。

功率谱估计 matlab
在MATLAB中进行功率谱密度估计可以使用多种方法,其中最常
用的是基于信号处理工具箱中的函数。
功率谱密度估计是一种用于
分析信号频谱特性的方法,它可以帮助我们了解信号中不同频率成
分的能量分布情况。
在MATLAB中,可以使用periodogram函数来对信号进行功率谱
密度估计。
该函数可以接受原始信号作为输入,并返回频率和对应
的功率谱密度估计值。
另一个常用的函数是pwelch,它可以对信号
进行Welch方法的功率谱估计,该方法是一种常用的频谱估计方法,可以减小估计值的方差。
除了这些内置函数,MATLAB还提供了其他一些工具和函数用于
功率谱密度估计,比如spectrogram函数用于计算信号的短时功率
谱密度估计,cpsd函数用于计算信号的交叉功率谱密度估计等。
在进行功率谱密度估计时,需要注意选择合适的窗函数、重叠
比例等参数,以保证估计结果的准确性和可靠性。
此外,还需要考
虑信号长度、采样频率等因素对功率谱密度估计的影响。
总之,在MATLAB中进行功率谱密度估计有多种方法和工具可供选择,需要根据具体的应用场景和要求来选择合适的方法和函数进行使用。
希望这些信息能对你有所帮助。

在matlab中,功率谱估计是信号处理和频谱分析中常用的一种方法。
通过对信号的频谱特性进行估计,可以有效地分析信号的功率分布情况,从而为信号处理和系统设计提供重要的参考信息。
在matlab中,提供了多种功率谱估计的函数,以下将对其中几种常用的函数进行介绍和分析。
1. periodogram函数periodogram函数是matlab中用于估计信号功率谱密度的函数之一。
它基于傅里叶变换将离散时间信号转换成频域信号,然后计算频域信号的功率谱密度。
其调用格式为:[Pxx, F] = periodogram(x,window,nfft,fs)其中,x为输入的离散时间信号,window为窗函数,nfft为离散傅里叶变换的点数,fs为信号的采样频率。
periodogram函数返回的Pxx 为功率谱密度估计值,F为对应的频率。
2. pwelch函数pwelch函数也是用于估计功率谱密度的函数,它采用了Welch方法,通过对信号进行分段处理,然后对各段信号进行傅里叶变换,并对各段功率谱密度进行平均。
其调用格式为:[Pxx, F] = pwelch(x,window,noverlap,nfft,fs)其中,x为输入的离散时间信号,window为窗函数,noverlap为相邻分段的重叠点数,nfft为离散傅里叶变换的点数,fs为信号的采样频率。
pwelch函数返回的Pxx为功率谱密度估计值,F为对应的频率。
3. cpsd函数cpsd函数用于估计信号的交叉功率谱密度,即两个信号之间的频谱特性。
其调用格式为:[Pxy, F] = cpsd(x,y,window,noverlap,nfft,fs)其中,x和y为输入的两个离散时间信号,window为窗函数,noverlap为相邻分段的重叠点数,nfft为离散傅里叶变换的点数,fs为信号的采样频率。
cpsd函数返回的Pxy为交叉功率谱密度估计值,F为对应的频率。
4. mscohere函数mscohere函数用于估计信号的相干函数,即两个信号之间的相关性。


基于M a t l a b 实现现代功率谱估计王春兴山东师范大学物理与电子科学学院,山东济南250014摘要:功率谱估计可以分为经典谱估计和现代谱估计。
现代谱的估计可建立A R 模型对离散信号进行谱估计、建立 M A 模型和A R M A 模型进行谱估计。
基于M a t l a b 对三种模型进行仿真,并对结果进行了分析。
结果显示,三种模型对现代谱的获得是有效的,并得到较好的谱估计。
P S E ;现代功率谱估计;A R 模型法; A R M AT N 911-34; G 202A 1004-373X (2011 16-0065-03M o d e r n P o w e r S p e c t r u m E s t i m a t i o n B a s e d o nM a t l a bW A N G C h u n -x i n g2011-03-26国家自然科学基金项目资助(10874103万方数据66万方数据@@[1]伊鑫,曲爱华. 基于W e l c h 算法的经典功率谱估计的M a t l a b分析[J ]. 现代电子技术,2010,33(3 :7-8.@@[2]王晓峰,王炳和. 周期图及其改进方法中谱分析率的M a t l a b分析[J ]. 武警工程学院学报,2003(6 :64-65.@@[3]宋宁,关华. 经典功率谱估计及其仿真[J ]. 现代电子技术,2008,31(11 :159-162.@@[4]冯磊. 经典功率谱估计与现代功率谱估计的对比[J ]. 商业文化, 2009(5 :182-183.@@[5]宁长春,陈天禄,索郎桑姆,等. 数字信号处理中常用的M a t l a b 工具箱函数简介[J ]. 西藏科技,2007(12 :75-77. @@[6]魏鑫,张平. 周期图法功率谱估计中的窗函数分析[J ]. 现代电子技术, 2005,28(3 :14-15.@@[7]邵玉斌. M a t l a b /S i m u l i n k 通信系统建模与仿真实例分析[M ]. 北京:清华大学出版社,2008.@@[8]范瑜 ,邬正义. 功率谱估计的W e l c h 方法中的窗函数研究[J ]. 常熟高专学报,2000, 14(7 :36-39.@@[9]瞿海雁,李鹂,钱小凌. 如何在M a t l a b 中优化基本周期图法对随机信号进行的功率谱估计[J ]. 首都师范大学学报:自然科学版,2006(5 :33-36.@@[10]罗敏, 刘嵩. 基于W e l c h 算法的功率谱估计的实现 [J ]. 北京工商大学学报 :自然科学版, 2007(3 : 58-59.@@[11] K A Y S M . M o d e r n s p e c t r a l e s t i m a t i o n :t h e o r y a n d a p p l i c a t i o n [M ]. N J : P r e n t i c e H a l l , 1998.@@[12]王玉德. 数字信号处理[M ]. 北京:北京大学出版社,2010. 王春兴男, 1962年出生, 博士, 副教授。

功率谱密度估计方法的MATLAB实现功率谱密度估计是信号处理领域中常用的一种方法,用于分析信号的频率特性。
MATLAB提供了多种功率谱密度估计方法的函数,包括传统的傅里叶变换方法和更现代的自相关方法。
以下是一些常见的功率谱密度估计方法及其MATLAB实现。
1.傅里叶变换方法:傅里叶变换方法是最常用的功率谱密度估计方法之一、MATLAB提供了`pwelch`函数来实现傅里叶变换方法的功率谱密度估计。
以下是一个简单的使用例子:```matlabfs = 1000; % 采样率t = 0:1/fs:1-1/fs; % 时间序列x = cos(2*pi*50*t) + randn(size(t)); % 生成一个包含50 Hz 正弦波和噪声的信号[Pxx, f] = pwelch(x, [],[],[], fs); % 估计功率谱密度plot(f, 10*log10(Pxx)); % 画出功率谱密度曲线xlabel('Frequency (Hz)');ylabel('Power Spectral Density (dB/Hz)');```2.自相关方法:自相关方法是另一种常用的功率谱密度估计方法。
MATLAB提供了`pcov`函数来实现自相关方法的功率谱密度估计。
以下是一个简单的使用例子:```matlabfs = 1000; % 采样率t = 0:1/fs:1-1/fs; % 时间序列x = cos(2*pi*50*t) + randn(size(t)); % 生成一个包含50 Hz 正弦波和噪声的信号[Rxx, lags] = xcorr(x, 'biased'); % 估计自相关函数[Pxx, f] = pcov(Rxx, [], fs, length(x)); % 估计功率谱密度plot(f, 10*log10(Pxx)); % 画出功率谱密度曲线xlabel('Frequency (Hz)');ylabel('Power Spectral Density (dB/Hz)');```3.周期图方法:周期图方法是一种能够处理非平稳信号的功率谱密度估计方法。
![[matlab实现经典功率谱估计]matlab功率谱估计](https://uimg.taocdn.com/acd3e43931b765ce04081407.webp)
[matlab实现经典功率谱估计]matlab功率谱估计1、直接法:直接法又称周期图法,它是把随机序列x(n)的N个观测数据视为一能量有限的序列,直接计算x(n)的离散傅立叶变换,得X(k),然后再取其幅值的平方,并除以N,作为序列x(n)真实功率谱的估计。
Matlab代码示例:clear;Fs=1000; %采样频率n=0:1/Fs:1;%产生含有噪声的序列xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n)); window=boxcar(length(xn)); %矩形窗nfft=1024;[Pxx,f]=periodogram(xn,window,nfft,Fs); %直接法plot(f,10*log10(Pxx));2、间接法:间接法先由序列x(n)估计出自相关函数R(n),然后对R(n)进行傅立叶变换,便得到x(n)的功率谱估计。
Matlab代码示例:clear;Fs=1000; %采样频率n=0:1/Fs:1;%产生含有噪声的序列xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n)); nfft=1024;cxn=xcorr(xn,”unbiased”); %计算序列的自相关函数CXk=fft(cxn,nfft);Pxx=abs(CXk);index=0:round(nfft/2-1);k=index*Fs/nfft;plot_Pxx=10*log10(Pxx(index+1));plot(k,plot_Pxx);3、改进的直接法:对于直接法的功率谱估计,当数据长度N太大时,谱曲线起伏加剧,若N太小,谱的分辨率又不好,因此需要改进。
3.1、Bartlett法Bartlett平均周期图的方法是将N点的有限长序列x(n)分段求周期图再平均。
Matlab代码示例:clear;Fs=1000;n=0:1/Fs:1;xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n)); nfft=1024;window=boxcar(length(n)); %矩形窗noverlap=0; %数据无重叠p=0.9; %置信概率[Pxx,Pxxc]=psd(xn,nfft,Fs,window,noverlap,p);index=0:round(nfft/2-1);k=index*Fs/nfft;plot_Pxx=10*log10(Pxx(index+1));plot_Pxxc=10*log10(Pxxc(index+1));figure(1)plot(k,plot_Pxx);pause;figure(2)plot(k,[plot_Pxx plot_Pxx-plot_Pxxc plot_Pxx+plot_Pxxc]);3.2、Welch法Welch法对Bartlett法进行了两方面的修正,一是选择适当的窗函数w(n),并再周期图计算前直接加进去,加窗的优点是无论什么样的窗函数均可使谱估计非负。

MATLAB仿真实现功率谱估计功率谱估计是信号处理中常用的一种技术,用于分析信号的频谱特征。
自相关法是一种常用的功率谱估计方法,在MATLAB中可以很方便地实现。
自相关法的基本原理是首先对信号进行自相关运算,然后对自相关结果进行傅里叶变换,最后求得功率谱。
下面将详细介绍如何在MATLAB中使用自相关法实现功率谱估计。
首先,我们需要生成一个待分析的信号。
假设我们生成一个长度为N的随机信号x,可以使用randn函数生成一个均值为0、方差为1的随机数序列,然后使用fft函数求得x的傅里叶变换。
```matlabN=1024;%信号长度Fs=1000;%采样率t=(0:N-1)/Fs;%时间向量x = randn(1, N); % 生成随机信号X = fft(x); % 计算信号的傅里叶变换```接下来,我们可以使用MATLAB的xcorr函数对信号进行自相关运算,得到自相关结果。
```matlabrxx = xcorr(x); % 自相关运算```得到自相关结果后,我们可以对rxx进行归一化处理,即将结果除以信号长度,以消除信号长度对功率谱估计的影响。
```matlabrxx = rxx / N; % 归一化处理```然后,我们可以对rxx进行傅里叶变换,得到信号的功率谱。
```matlabPxx = fftshift(abs(fft(rxx))); % 功率谱估计f=(-N/2:N/2-1)*Fs/N;%频率向量```最后,我们可以使用plot函数将结果画出来,以便进行观察和分析。
```matlabfigure;plot(f, Pxx);xlabel('频率(Hz)');ylabel('功率谱');title('信号的功率谱估计');```通过以上步骤,我们就完成了MATLAB中利用自相关法实现功率谱估计的过程。
可以通过改变信号的长度N、采样率Fs以及噪声的统计特性等参数,观察估计结果的精确性和稳定性。

在MATLAB中,计算功率谱是信号处理和频谱分析中的重要任务。
功率谱可以帮助我们了解信号中不同频率成分的能量分布情况,对于理解信号特性和进行频谱分析都是至关重要的。
在MATLAB中,有多种方法可以用来计算功率谱,在本文中,我将介绍并比较其中的四种常用方法。
第一种方法是使用MATLAB中的`periodogram`函数。
`periodogram`函数可以直接计算信号的功率谱密度(PSD),它采用傅里叶变换的方法,将信号从时域转换到频域,并计算功率谱密度。
这种方法简单直接,适用于对功率谱快速估计的情况。
在使用`periodogram`函数时,我们可以指定窗函数和重叠比例等参数,来对功率谱的估计进行优化。
第二种方法是使用`pwelch`函数。
`pwelch`函数也可以用来计算信号的功率谱密度,它采用Welch方法,通过对信号进行分段,然后对每个段进行傅里叶变换,并对结果进行平均来估计功率谱密度。
Welch 方法可以减小估计的方差,得到更平滑和可靠的功率谱估计结果。
在使用`pwelch`函数时,同样可以指定窗函数和重叠比例等参数来优化估计结果。
第三种方法是使用`fft`函数和自行计算功率谱。
通过对信号进行傅里叶变换得到频谱,然后对频谱的幅度进行平方运算,即可得到功率谱。
这种方法的好处是灵活性高,可以根据具体需求对傅里叶变换和求平方的结果进行后续处理,比如进行平滑或滤波操作。
但是需要注意的是,自行计算功率谱需要对信号处理和频谱分析有较深的理解。
第四种方法是使用`cpsd`函数。
`cpsd`函数可以用来计算信号之间的交叉功率谱密度,适用于多信号系统中不同信号之间的频谱分析。
交叉功率谱密度可以帮助我们理解不同信号之间频率成分的相关性和影响程度,对于系统建模和故障诊断都是非常有帮助的。
MATLAB提供了多种方法来计算功率谱,每种方法都有其适用的场景和优势。
在具体应用中,我们可以根据信号特性和分析需求来选择合适的方法。
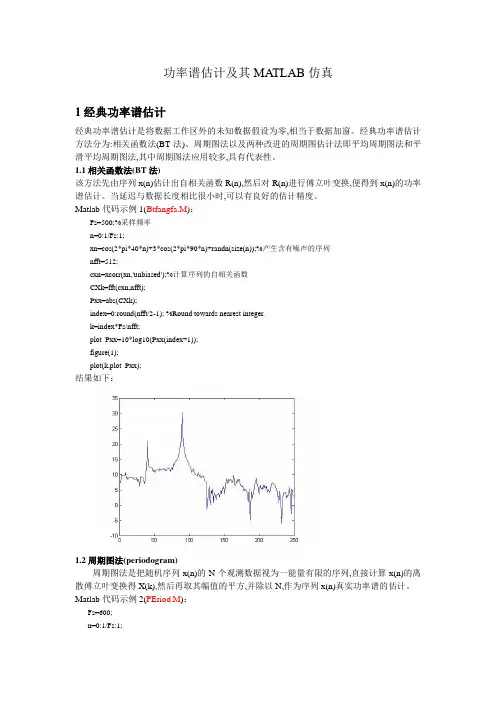
功率谱估计及其MATLAB仿真1经典功率谱估计经典功率谱估计是将数据工作区外的未知数据假设为零,相当于数据加窗。
经典功率谱估计方法分为:相关函数法(BT法)、周期图法以及两种改进的周期图估计法即平均周期图法和平滑平均周期图法,其中周期图法应用较多,具有代表性。
1.1相关函数法(BT法)该方法先由序列x(n)估计出自相关函数R(n),然后对R(n)进行傅立叶变换,便得到x(n)的功率谱估计。
当延迟与数据长度相比很小时,可以有良好的估计精度。
Matlab代码示例1(Btfangfa.M):Fs=500;%采样频率n=0:1/Fs:1;xn=cos(2*pi*40*n)+3*cos(2*pi*90*n)+randn(size(n));%产生含有噪声的序列nfft=512;cxn=xcorr(xn,'unbiased');%计算序列的自相关函数CXk=fft(cxn,nfft);Pxx=abs(CXk);index=0:round(nfft/2-1); %Round towards nearest integer.k=index*Fs/nfft;plot_Pxx=10*log10(Pxx(index+1));figure(1);plot(k,plot_Pxx);结果如下:1.2周期图法(periodogram)周期图法是把随机序列x(n)的N个观测数据视为一能量有限的序列,直接计算x(n)的离散傅立叶变换得X(k),然后再取其幅值的平方,并除以N,作为序列x(n)真实功率谱的估计。
Matlab代码示例2(PEriod.M):Fs=600;n=0:1/Fs:1;xn=cos(2*pi*40*n)+3*cos(2*pi*90*n)+randn(size(n));window=boxcar(length(xn));%矩形窗nfft=512;[Pxx,f]=periodogram(xn,window,nfft,Fs);%直接法figure(1);plot(f,10*log10(Pxx));window=boxcar(length(xn));%矩形窗nfft=1024;[Pxx,f]=periodogram(xn,window,nfft,Fs);%直接法figure(2);plot(f,10*log10(Pxx));结果如下:1.3平均周期图法和平滑平均周期图法对于周期图的功率谱估计,当数据长度N太大时,谱曲线起伏加剧,若N太小,谱的分辨率又不好,因此需要改进。
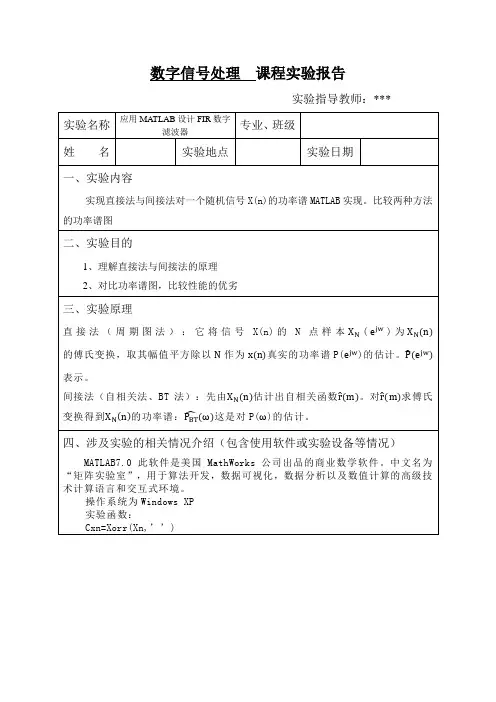
用matlab做经典功率谱估计经典功率谱估计1、直接法:直接法又称周期图法,它是把随机序列x(n)的N个观测数据视为一能量有限的序列,直接计算x(n)的离散傅立叶变换,得X(k),然后再取其幅值的平方,并除以N,作为序列x(n)真实功率谱的估计。
Matlab代码示例:clear;Fs=1000; %采样频率n=0:1/Fs:1;%产生含有噪声的序列xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));window=boxcar(length(xn)); %矩形窗nfft=1024;[Pxx,f]=periodogram(xn,window,nfft,Fs); %直接法plot(f,10*log10(Pxx));2、间接法:间接法先由序列x(n)估计出自相关函数R(n),然后对R(n)进行傅立叶变换,便得到x(n)的功率谱估计。
Matlab代码示例:clear;Fs=1000; %采样频率n=0:1/Fs:1;%产生含有噪声的序列xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));nfft=1024;cxn=xcorr(xn,'unbiased'); %计算序列的自相关函数CXk=fft(cxn,nfft);Pxx=abs(CXk);index=0:round(nfft/2-1);k=index*Fs/nfft;plot_Pxx=10*log10(Pxx(index+1));plot(k,plot_Pxx);3、改进的直接法:对于直接法的功率谱估计,当数据长度N太大时,谱曲线起伏加剧,若N 太小,谱的分辨率又不好,因此需要改进。
3.1、Bartlett法Bartlett平均周期图的方法是将N点的有限长序列x(n)分段求周期图再平均。
Matlab代码示例:clear;Fs=1000;n=0:1/Fs:1;xn=cos(2*pi*40*n)+3*cos(2*pi*100*n)+randn(size(n));nfft=1024;window=boxcar(length(n)); %矩形窗noverlap=0; %数据无重叠p=0.9; %置信概率[Pxx,Pxxc]=psd(xn,nfft,Fs,window,noverlap,p);index=0:round(nfft/2-1);k=index*Fs/nfft;plot_Pxx=10*log10(Pxx(index+1));plot_Pxxc=10*log10(Pxxc(index+1));figure(1)plot(k,plot_Pxx);pause;figure(2)plot(k,[plot_Pxx plot_Pxx-plot_Pxxc plot_Pxx+plot_Pxxc]);3.2、Welch法Welch法对Bartlett法进行了两方面的修正,一是选择适当的窗函数w(n),并再周期图计算前直接加进去,加窗的优点是无论什么样的窗函数均可使谱估计非负。
【转】matlab的功率谱计算功率谱估计在现代信号处理中是一个很重要的课题,涉及的问题很多。
在这里,结合matlab,我做一个粗略介绍。
功率谱估计可以分为经典谱估计方法与现代谱估计方法。
经典谱估计中最简单的就是周期图法,又分为直接法与间接法。
直接法先取N点数据的傅里叶变换(即频谱),然后取频谱与其共轭的乘积,就得到功率谱的估计;间接法先计算N点样本数据的自相关函数,然后取自相关函数的傅里叶变换,即得到功率谱的估计.都可以编程实现,很简单。
在matlab中,周期图法可以用函数periodogram实现。
但是周期图法估计出的功率谱不够精细,分辨率比较低。
因此需要对周期图法进行修正,可以将信号序列x(n)分为n个不相重叠的小段,分别用周期图法进行谱估计,然后将这n段数据估计的结果的平均值作为整段数据功率谱估计的结果。
还可以将信号序列x(n)重叠分段,分别计算功率谱,再计算平均值作为整段数据的功率谱估计。
这2种称为分段平均周期图法,一般后者比前者效果好。
加窗平均周期图法是对分段平均周期图法的改进,即在数据分段后,对每段数据加一个非矩形窗进行预处理,然后在按分段平均周期图法估计功率谱。
相对于分段平均周期图法,加窗平均周期图法可以减小频率泄漏,增加频峰的宽度。
welch法就是利用改进的平均周期图法估计估计随机信号的功率谱,它采用信号分段重叠,加窗,FFT等技术来计算功率谱。
与周期图法比较,welch法可以改善估计谱曲线的光滑性,大大提高谱估计的分辨率。
matlab中,welch法用函数psd实现。
调用格式如下:[Pxx,F] = PSD(X,NFFT,Fs,WINDOW,NOVERLAP)X:输入样本数据NFFT:FFT点数Fs:采样率WINDOW:窗类型NOVERLAP,重叠长度现代谱估计主要针对经典谱估计分辨率低和方差性不好提出的,可以极大的提高估计的分辨率和平滑性。
可以分为参数模型谱估计和非参数模型谱估计。
功率谱估计性能分析及其MATLAB实现一、经典功率谱估计分类简介1.间接法根据维纳-辛钦定理,1958年Blackman和Turkey给出了这一方法的具体实现,即先由N个观察值,估计出自相关函数,求自相关函数傅里叶变换,以此变换结果作为对功率谱的估计。
2.直接法直接法功率谱估计是间接法功率谱估计的一个特例,又称为周期图法,它是把随机信号的N 个观察值直接进行傅里叶变换,得到,然后取其幅值的平方,再除以N,作为对功率谱的估计。
3.改进的周期图法将N点的观察值分成L个数据段,每段的数据为M,然后计算L个数据段的周期图的平均,作为功率谱的估计,以此来改善用N点观察数据直接计算的周期图的方差特性。
根据分段方法的不同,又可以分为Welch法和Bartlett法。
Welch法所分的数据段可以互相重叠,选用的数据窗可以是任意窗。
Bartlett法所分的数据段互不重叠,选用的数据窗是矩形窗。
二、经典功率谱估计的性能比较1.仿真结果为了比较经典功率谱估计的性能,本文采用的信号是高斯白噪声加两个正弦信号,采样率Fs=1000Hz,两个正弦信号的频率分别为f1=200Hz,f2=210Hz。
所用数据长度N=400.仿真结果如下:(a)(b)(c)(d)(e)(f)Figure1经典功率谱估计的仿真结果Figure1(a)示出了待估计信号的时域波形;Figure2(b)示出了用该数据段直接求出的周期图,所用的数据窗为矩形窗;Figure2(c)是用BT法(间接法)求出的功率谱曲线,对自相关函数用的平滑窗为矩形窗,长度M=128,数据没有加窗;Figure2(d)是用BT法(间接法)求出的功率谱曲线,对自相关函数用的平滑窗为Hamming 窗,长度M=64,数据没有加窗;Figure2(e)是用Welch平均法求出的功率谱曲线,每段数据的长度为64点,重叠32点,使用的Hamming窗;Figure2(f)是用Welch平均法求出的功率谱曲线,每段数据的长度为100点,重叠48点,使用的Hamming窗;2.性能比较1)直接法得到的功率谱分辨率最高,但是方差性能最差,功率谱起伏剧烈,容易出现虚假谱峰;2)间接法由于使用了平滑窗对直接法估计的功率谱进行了平滑,因此方差性能比直接法好,功率谱比直接法估计的要平滑,但其分辨率比直接法低。
一、作业内容:对两个正弦信号做叠加后,计算离散随机进程信号的功率谱函数,由功率谱,估量信号的频率。
在matlab上实现之,并观察波形进行验证。
二、实现步骤:(一)、构造环境:一、两个正弦波别离为A*sin(2*pi*f1*n+a)、B*sin(2*pi*f2*n+a),规定取样点范围n=1~128;构造函数x1=A*sin(2*pi*f1*n+a)+B*sin(2*pi*f2*n+a);二、在x1基础上加入加性高斯白噪声,取定信噪比为+3,来概念x2的函数为x2=x1+W(噪声);3、对离散信号x2做非参数化谱估量,以傅里叶变换为基础,先对x2做傅里叶变换,求出其频谱;4、求x2的功率谱p(w),用周期图法;用间接法;别离估量做出功率谱,并输出其功率谱波形。
五、更改采样点数,验证功率谱波形的主瓣函数图形什么情况下有重叠程度、什么情况下能够很好的区分开来。
(二)、在matlab中编写相应程序:clear all; %清除工作空间所有之前的变量close all; %关闭之前的所有的figureclc; %清除命令行之前所有的文字n=1:1:128; %设定采样点n=1-128f1=0.2; %设定f1频率的值0.2f2=0.213; %设定f2频率的值0.213A=1; %取定第一个正弦函数的振幅B=1; %取定第一个正弦函数的振幅a=0; %设定相位为0x1=A*sin(2*pi*f1*n+a)+B*sin(2*pi*f2*n+a); %概念x1函数,不添加高斯白噪声x2=awgn(x1,3); %在x1基础上添加加性高斯白噪声,信噪比为3,概念x2函数temp=0; %概念临时值,并规定初始值为0temp=fft(x2,128); %对x2做快速傅里叶变换pw1=abs(temp).^2/128; %对temp做经典功率估量k=0:length(temp)-1;w=2*pi*k/128;figure(1); %输出x1函数图像plot(w/pi/2,pw1) %输出功率谱函数pw1图像xlabel('信号频率/Hz');ylabel('PSD/傅立叶功率谱估量');title('正弦信号x1添加高斯白噪声后的,周期图法功率频谱分析');grid;%-------------------------------------------------------------------------pw2=temp.*conj(temp)/128; %对temp做向量的共轭乘积k=0:length(temp)-1;w=2*pi*k/128;figure(2);plot(w/pi/2,pw2); %输出功率谱函数pw2图像xlabel('信号频率/Hz');ylabel('PSD/傅立叶功率谱估量');title('正弦信号x1自相关法功率谱估量');grid;三、在matlab中,输出的功率谱图像。
上机作业:1、假设一平稳随机信号为()()()0.81x n x n w n =−+,其中 是均值为0,方差为1的白噪声,数据长度为1024。
(1)、产生符合要求的)(n w 和)(n x ;(2)、给出信号)(n x 的理想功率谱;(3)、编写周期图谱估计函数,估计数据长度N=1024及256时信号功率谱,分析估计效果。
(4)、编写Bartlett 平均周期图函数,估计当数据长度N=1024及256时,分段数L 分别为2和8时信号 的功率谱,分析估计效果。
一、解题思路w(n)可以通过随机序列randn(1,N)来产生,x(n)可以通过对w(n)滤波产生(由递推式可得系统的传递函数),也可以直接由递推式迭代产生。
由于线性系统的输出功率谱等于输入功率谱乘以传递函数模的平方,X(n)可以看做w(n)通过一线性系统的输出,H(z)=1/(1-0.8z)。
所以x(n)的理想功率谱P(e jw )=σw 2|H(e jw )|2。
周期图方法:直接对观测数据做FFT 变换,变换的结果取模的平方再除以数据长度,作为估计的功率谱。
256个观测点时可以对原观测数据以4为间隔提取得到。
Bartlett 法:将L 组独立的观测数据分别求周期图,再将L 个周期图求平均作为信号的功率谱估计。
L 组数据可以通过对原观测数据以L 为间隔提取得到。
二、MATLAB 实现程序及注解 clc;clear;close all;Fs=500; %采样率N=1024; %观测数据w=sqrt(1)+randn(1,N); %0均值,方差为1的白噪声,长度1024x=[w(1) zeros(1,N-1)]; %初始化x(n),长度1024,x(1)=w(1)for i=2:Nx(i)=0.8*x(i-1)+w(i); %迭代产生观测数据x(n)end%% 理想功率谱[h,w1]=freqz(x);figure,plot(w1*500/(2*pi),10*log10(abs(h).^2));grid on;title('理想功率谱');xlabel('频率'); ylabel('功率db');%% 周期图法%1024个观测点Pxx=abs(fft(x)).^2/N; %周期图公式Pxx=10*log10(Pxx(index+1)); %化为dbfigure;plot(k,Pxx);grid on;title('周期图1024点');xlabel('频率'); ylabel('功率db');% 周期图256个观测点x1=x(1:4:N);Pxx1=abs(fft(x1,1024)).^2/N;Pxx1=10*log10(Pxx1(index+1)); %化为dbfigure;plot(k,Pxx1);grid on;title('周期图256点');xlabel('频率'); ylabel('功率db');%% Bartlett平均周期图,N=1024%分段L=2L=2;x_21=x(1:L:N);x_22=x(2:L:N);Pxx_21=abs(fft(x_21,1024)).^2/length(x_21);Pxx_22=abs(fft(x_22,1024)).^2/length(x_22);Pxx_2=(Pxx_21+Pxx_22)/L;figure;subplot(2,2,1),plot(k,10*log10(Pxx_2(index+1)));grid on;title('N=1024,L=2');xlabel('频率'); ylabel('功率db');%分段L=8L1=8;x3=zeros(L1,N/L1); %产生L1行,N/L1列的矩阵用以存储分组的数据for i=1:L1x3(i,:)=x(i:L1:N); %将原始数据分为8组endPxx3=zeros(L1,1024); %产生L1行,1024列矩阵用以存储分组的周期图for i=1:L1Pxx3(i,:)=abs(fft(x3(i,:),1024)).^2/length(x3(i,:)); %分别求周期图,结果保存在Pxx3中,FFT长度为1024endfor i=1:1024Pxx3_m(i)=sum(Pxx3(:,i))/L1; %求平均endsubplot(2,2,2),plot(k,10*log10(Pxx3_m(index+1)));grid on;title('N=1024,L=8');xlabel('频率'); ylabel('功率db');%% Bartlett平均周期图,N=256,求法同上%分段L=2,分别计算周期图,再取平均x=x(1:4:N);L2=2;x_31=x(1:L2:length(x));x_32=x(2:L2:length(x));Pxx_31=abs(fft(x_31,1024)).^2/length(x_31);Pxx_32=abs(fft(x_32,1024)).^2/length(x_32);Pxx_3=(Pxx_31+Pxx_32)/L2;subplot(2,2,3),plot(k,10*log10(Pxx_3(index+1)));grid on;title('N=256,L=2');xlabel('频率'); ylabel('功率db');%分段L=8L3=8;x4=zeros(L3,length(x)/L3);for i=1:L3x4(i,:)=x(i:L3:length(x)); %将原始数据分为8组endPxx4=zeros(L3,1024);for i=1:L3Pxx4(i,:)=abs(fft(x4(i,:),1024)).^2/length(x4(i,:)); %分别求周期图,FFT长度为1024endfor i=1:1024Pxx4_m(i)=sum(Pxx4(:,i))/L3; %求平均endsubplot(2,2,4),plot(k,10*log10(Pxx4_m(index+1)));grid on;title('N=256,L=8');xlabel('频率'); ylabel('功率db');三、结果及分析图1 理想功率谱图2 周期图1024点及256点从上图可以看出,周期图法得到的功率谱估计,谱线的起伏较大,即估计所得的均方误差较大。
当N增加时,摆动的频率加快,而摆动的幅度变化不大。
且N=1024时,谱的分辨率较N=256时大。
图3 Bartlett平均周期图法由上图可以看出,采用平均处理后,谱线上下摆动的幅度减小(即均方误差有所降低),曲线的平滑性也较周期图法好。
N相同时,分段越多,方差越小,曲线越平滑。
这是因为,N一定时,L加大,每一段的数据量就会相应减少,因此估计方差减小,偏移加大,从而分辨率降低。
N一定时,L与每段数据量相互矛盾,需择中选取。
综上,Bartlett法相对于周期图法来说,较好地减小了估计误差。
2、假设均值为0,方差为1的白噪声w(n)中混有两个正弦信号,该正弦信号的频率分别为100Hz和110Hz,信噪比分别为10dB和30dB,初始相位都为0,采样频率为1000Hz。
(1)、采用自相关法、Burg法、协方差法、修正协方差法估计功率谱,分析数据长度和模型阶次对估计结果的影响(可采用MATLAB自带的功率谱分析函数)。
(2)、调整正弦信号信噪比,分析信噪比的降低对估计效果的影响。
一、解题思路信噪比为信号平均功率与噪声的平均功率之比,即SNR=10lgS/N,单位dB。
假设正弦信号的幅度为A,对其在一个周期内的平方进行积分再除以周期长度可得,平均功率P s=A2/2。
白噪声的平均功率为1,所以又SNR的计算式可得题中两个正弦信号的幅值分别为sqrt(20)和sqrt(2000)。
题中,所给观测信号为白噪声混有两个正弦信号,所以功率谱中应有两个明显的尖峰,所以选择AR模型来进行估计。
AR模型的估计方法有自相关法,Burg法,协方差法和修正协方差法等。
本次编程采用matlab自带的功率谱分析函数。
自相关,Burg法,协方差法,修正协方差法分别为pyulear(),pburg(),pcov(),pmcov()。
二、MATlAB实现程序及注解clc;clear;close all;fs=1000;%采样率1000N=1;%改变数据长度p=50;%AR模型阶数nfft=512;%fft长度t=0:1/fs:N;wn=sqrt(1)+randn(1,N*fs+1); %白噪声,均值0,方差1s1=sqrt(20)*sin(2*pi*100*t); %正弦信号1,信噪比10dbs2=sqrt(2000)*sin(2*pi*110*t); %正弦信号2,信噪比30dbx=s1+s2+wn; %观测数据%figure,plot(t,x);x1=xcorr(x,'biased');[Pxx,f]=pyulear(x1,p,nfft,fs); %Yule-Walker方程figure,plot(f,10*log10(Pxx));grid on;title('自相关法');[Pxx1,f1]=pcov(x,p,nfft,fs);figure,plot(f1,10*log10(Pxx1));grid on;title('协方差法');[Pxx2,f2]=pmcov(x,p,nfft,fs);figure,plot(f2,10*log10(Pxx2));grid on;title('修正协方差法');[Pxx3,f3]=pburg(x,p,nfft,fs);figure,plot(f3,10*log10(Pxx3));grid on;title('Burg法');三、结果及分析图1 50阶AR模型谱估计从上图可以看出,采用参数建模的谱估计方法得到的功率谱曲线平滑(方差小),分辨率高,可以明显地观察到两个谱峰。
图2 20阶AR模型谱估计降低模型阶次后,可以发现,谱的分辨率降低(两个谱峰几乎变成一个谱峰),但是曲线平滑性变好(估计误差降低)。
图3 50阶AR模型(4倍观测数据)谱估计与图1相比,图3几乎没有什么变化,这是因为AR模型隐含着数据的外推。