[工学]电路原理第三章

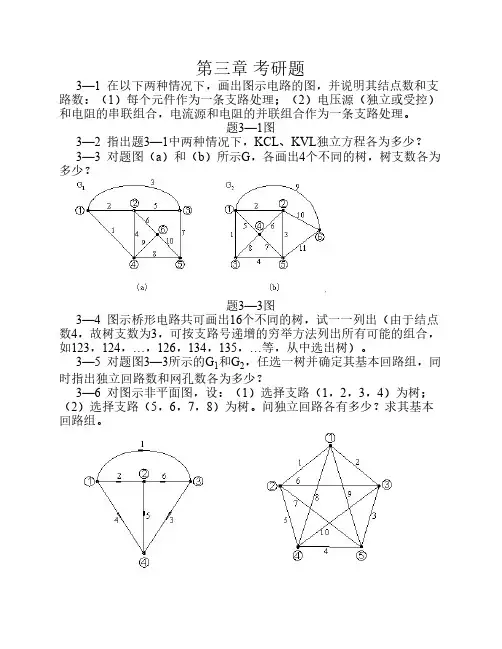
第三章考研题
3—1 在以下两种情况下，画出图示电路的图，并说明其结点数和支路数：（1）每个元件作为一条支路处理；（2）电压源（独立或受控）和电阻的串联组合，电流源和电阻的并联组合作为一条支路处理。

题3—1图
3—2 指出题3—1中两种情况下，KCL、KVL独立方程各为多少？
3—3 对题图（a）和（b）所示G，各画出4个不同的树，树支数各为多少？
题3—3图
3—4 图示桥形电路共可画出16个不同的树，试一一列出（由于结点数4，故树支数为3，可按支路号递增的穷举方法列出所有可能的组合，如123，124，…，126，134，135，…等，从中选出树）。

3—5 对题图3—3所示的G1和G2，任选一树并确定其基本回路组，同时指出独立回路数和网孔数各为多少？
3—6 对图示非平面图，设：（1）选择支路（1，2，3，4）为树；（2）选择支路（5，6，7，8）为树。

问独立回路各有多少？求其基本回路组。

题3—4图题3—6图3—7用结点电压法求解图示电路中电压U。

题3—7图
3—8 用结点电压法求解题3—8。

3—9 用结点电压法求解题3—9。

题3—8图
题3—9图
3—10 用结点电压法求解图示电路后，求各元件的功率并检验功率是否平衡。

题3—10图
3—11 用结点电压法求解图示电路中和，你对此题有什么看法？
题3—11图
3—12 列出图示电路的结点电压方程。

如果，则方程又如何？（提示：为避免引入过多附加电流变量，对连有无伴电压的结点部分，可在包含无伴电压源的封闭面S上写出KCL方程）。

题3—12图。

电路原理第三章第三章电阻电路的一般分析一、教学基本要求电路的一般分析是指方程分析法，是以电路元件的约束特性（VCR）和电路的拓补约束特性（KCL、KVL）为依据，建立以支路电流或回路电流或结点电压为变量的电路方程组，解出所求的电压、电流和功率。

方程分析法的特点是：（1）具有普遍适用性，即无论线性和非线性电路都适用；（2）具有系统性，表现在不改变电路结构，应用KCL，KVL，元件的VCR建立电路变量方程，方程的建立有一套固定不变的步骤和格式，便于编程和用计算机计算。

本章学习的内容有：电路的图，KCL和KVL的独立方程数，支路电流法，网孔电流法，回路电流法，结点电压法。

本章内容以基尔霍夫定律为基础。

介绍的支路电流法、回路电流法和节点电压法适用于所有线性电路问题的分析，在后面章节中都要用到。

内容重点：会用观察电路的方法，熟练应用支路电流法，回路电流法，结点电压法的“方程通式”写出支路电流方程，回路电流方程，结点电压方程，并求解。

预习知识：线性代数方程的求解难点：1. 独立回路的确定2. 正确理解每一种方法的依据3. 含独立电流源和受控电流源的电路的回路电流方程的列写4. 含独立电压源和受控电压源的电路的结点电压方程的列写二、学时安排总学时：6三、教学内容§3－1 电路的图1. 网络图论图论是拓扑学的一个分支，是富有趣味和应用极为广泛的一门学科。

图论的概念由瑞士数学家欧拉最早提出，欧拉在1736年发表的论文《依据几何位置的解题方法》中应用图的方法讨论了各尼斯堡七桥难题，见图3.1a和b所示。

图3.1 a 哥尼斯堡七桥 b 对应的图19～20世纪，图论主要研究一些游戏问题和古老的难题，如哈密顿图及四色问题。

1847年，基尔霍夫首先用图论来分析电网络，如今在电工领域，图论被用于网络分析和综合、通讯网络与开关网络的设计、集成电路布局及故障诊断、计算机结构设计及编译技术等等。

2. 电路的图电路的图是用以表示电路几何结构的图形，图中的支路和结点与电路的支路和结点一一对应，如图3.2所示，所以电路的图是点线的集合。

电路基础第三章知识点总结第三章节的内容主要涉及电路的分析和维持，包括各种电路的分析方法、戴维南定理、诺尔顿定理、极限定理、最大功率传输定理以及电路维持的相关知识。

通过本章的学习，我们可以更好地理解电路的工作原理和分析方法，为我们今后的学习和工作打下扎实的基础。

本篇总结将主要围绕本章的知识点展开，总结出电路的分析方法和维持知识点，让读者对电路有更全面的了解。

一、电路分析方法1.节点分析法节点分析法是一种电路分析方法，通过寻找电路中的节点，应用基尔霍夫电流定律（KCL）进行节点电压的分析。

通过节点电压的计算，可以找到各个支路中的电流，从而进一步分析电路的特性。

节点分析法的手续步骤为：（1）选取一个节点作为参考点，为了简化计算，一般选为电压源的负极或接地点；（2）对不确定电压的节点进行标记；（3）应用基尔霍夫电流定律，列出各节点处的电流之和为零；（4）利用基尔霍夫电流定律和欧姆定律，列出各节点处的电压。

2.支路分析法支路分析法是一种电路分析方法，通过寻找电路中的支路，应用基尔霍夫电压定律（KVL）进行支路电流和电压的分析。

通过支路电流和电压的计算，可以找到各个支路中的电流和电压，从而进一步分析电路的特性。

支路分析法的手续步骤为：（1）选择一个支路作为参考方向，可以沿着电流的方向或者反方向；（2）按照已选的方向，利用基尔霍夫电压定律，列出各支路的电流和电压；（3）应用欧姆定律，列出支路中的电流和电压。

3.戴维南定理戴维南定理是电路理论中的一项重要理论，它指出了任意线性电路可以用一个恒电压源和一个串联电流源的组合来替代。

通过戴维南定理，可以将一个复杂的电路简化为一个等效的电压源和串联电流源的组合，从而方便进一步的分析和计算。

4.诺尔顿定理诺尔顿定理是电路理论中的另一项重要理论，它指出了任意线性电路可以用一个恒电流源和一个并联电阻的组合来替代。

通过诺尔顿定理，可以将一个复杂的电路简化为一个等效的电流源和并联电阻的组合，从而方便进一步的分析和计算。

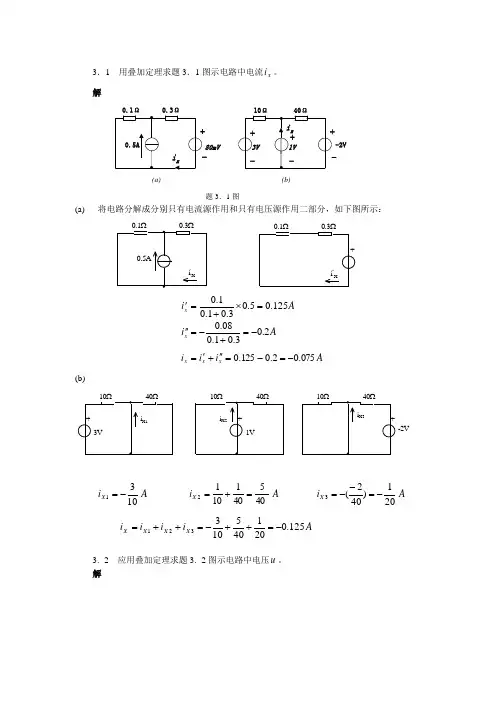
3．1 用叠加定理求题3．1图示电路中电流xi。

解0.3Ω(a)80mV0.1Ω(b)-2V题3．1图(a) 将电路分解成分别只有电流源作用和只有电压源作用二部分，如下图所示：Aix125.05.03.01.01.0=⨯+='Aix2.03.01.008.0-=+-=''Aiiixxx075.02.0125.0-=-=''+'=(b)-2V AiX1031-=AiX4054011012=+=AiX201)402(3-=--=AiiiiXXXX125.0201405103321-=++-=++=3．2 应用叠加定理求题3．2图示电路中电压u。

解136V题3．2图954413694136210//40810//401=⨯=⨯++=u38)3810//4022()10//40(2-=⨯++⨯-=u92005010//401010//403=⨯+=uVuuuu809200389544321=+-=++=3．3 应用叠加定理求题3．3图示电路中电压U。

解+-5V+2kΩ1kΩ-··-U2kΩ+10V1kΩ+-6U题3．3图分别对二个网孔采用顺时针方向写网孔电流方程：1k1k Ω10V(a )(b )对(a) U i i b a'-='-'++652)122( U i i b a'='++'-6)21(2 ai U '-=' 解得 mA i a3=' V k i U a 31-=Ω⨯'-=' 对(b) U i i b a''-=''-''++62)122( 106)21(2-''=''++''-U i i b aai U ''-='' 解得 mA i a4-='' V k i U a 41=Ω⨯''-='' V U U U 1)43(=+-=''+'=3．4 (a) 已知框图内的电路为无源电路，当V U S 1=，A I S 2=，V u 1-=V U S 2=，A I S 1-=，V u 5.5=问当 V U S 1-=，A I S 2-=， 则 ?=u(b) 已知框图内的电路为有源电路，可等效为一个电流源S I ，当 V U S 11=，V U S 22=，A I S 1=，A I 2= V U S 21=，V U S 5.12=，A I S 5.0=，A I 3= V U S 11-=，V U S 12=，A I S 1-=，A I 1-= 问当 V U S 5.11=，V U S 5.02=，A I S 2=，则 ?=IU S+_U S 2U S 1I(a) (b)题3．4图解(a) 根据线性叠加定理有 SSBIAUu +=将已知参数代入上式有 B A 21+=- B A -=25.5 解此联立方程有2=A Ω-=5.1B 这样就得到端口电压的方程表达式为 S S I U u 5.12-= 当 V US1-=，A I S 2-= 时，V u 1)2(5.1)1(2=-⨯--⨯=(b) 根据线性叠加定理有 SS S CIBUAUI ++=21将已知参数代入上式有C B A ++=22C B A 5.05.123++= C B A -+-=-1 解此联立方程有 911=A 31=B 91=C这样就得到端口电流的方程表达式为 S S S I UUI 913191121++=当VU S 5.11=，VU S 5.02=，AI S2= 时有A I 22.22915.0315.1911=⨯+⨯+⨯=3．7 试求图示电路中的I ，设2=g 。

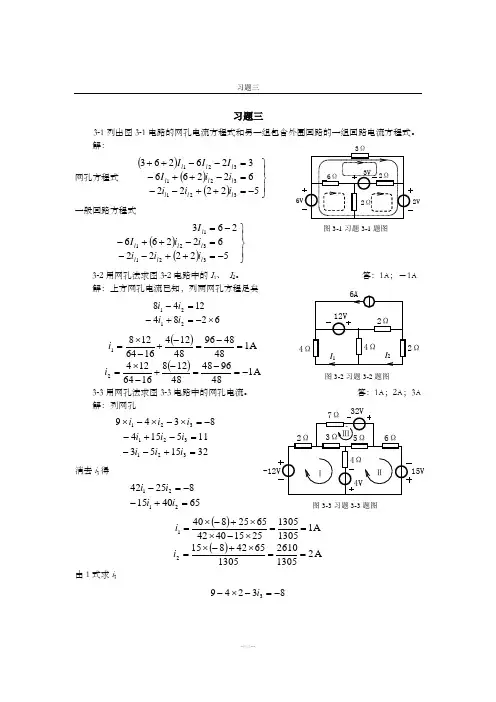
习题三习题三3-1列出图3-1电路的网孔电流方程式和另一组包含外围回路的一组回路电流方程式。

解： 网孔方程式 ()()()⎪⎭⎪⎬⎫-=++--=-++-=--++5222262266326263321321321l l l l l l l l l i i i i i I I I I一般回路方程式()()⎪⎭⎪⎬⎫-=++--=-++--=52222622662633213211l l l l l l l i i i i i I I 3-2用网孔法求图3-2电路中的I 1、 I 2。

答：1A ；－1A 解：上方网孔电流已知，列两网孔方程足矣628412482121⨯-=+-=-i i i i()A 14848964812416641281=-=-+-⨯=i()A 14896484812816641242-=-=-+-⨯=i3-3用网孔法求图3-3电路中的网孔电流。

答：1A ；2A ；3A解：列网孔32155********349321321321=+--=-+--=⨯-⨯-⨯i i i i i i i i i 消去i 3得654015825422121=+--=-i i i i()A 1130513052515404265258401==⨯-⨯⨯+-⨯=i()A 213052610130565428152==⨯+-⨯=i由1式求i 3832493-=-⨯-i2Ω图3-2习题3-2题图图3-3习题3-3题图图3-1习题3-1题图习题三A 3393==i 3-4用回路法求图3-4电路中的U 。

答：－6V 解：该电路有3个独立回路，设定两电流源为两个独立回路电流，则选左边回路列方程式可解()()1510363232=⨯+⨯+++iA 9545-=-=i()V 6962-=-=U3-5用回路法求图3-5电路中的各支路电流。

答：－1A ；－1A ；0；0；1A 解：1A 电流源为第3网孔电流，则列两个回路方程可解2421322121-=+-=-i i i i()1226823141-=-=--+⨯=i()122222122-=-=-+⨯=i0123=+=i i0124=-=i i i A 1135=-=i i i3-6在图3-6电路中，已知V 3=s U ，Ω=11R ，Ω=22R Ω=33R ，Ω=64R ，试用回路法求各支路电流及各电源功率。