[计算题]节约里程法
- 格式:doc
- 大小:61.50 KB
- 文档页数:3
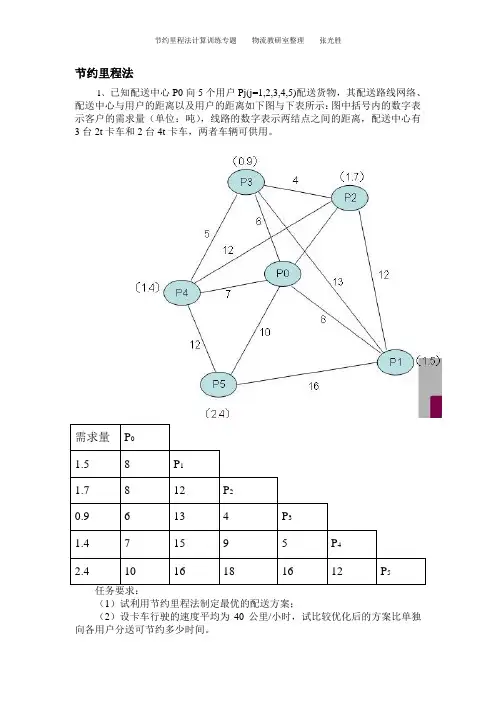
节约里程法1、已知配送中心P0向5个用户Pj(j=1,2,3,4,5)配送货物,其配送路线网络、配送中心与用户的距离以及用户的距离如下图与下表所示:图中括号内的数字表示客户的需求量(单位:吨),线路的数字表示两结点之间的距离,配送中心有3台2t卡车和2台4t卡车,两者车辆可供用。
需求量P01.5 8 P11.7 8 12 P20.9 6 13 4 P31.4 7 15 9 5 P42.4 10 16 18 16 12 P5(1)试利用节约里程法制定最优的配送方案;(2)设卡车行驶的速度平均为40公里/小时,试比较优化后的方案比单独向各用户分送可节约多少时间。
2、已知配送中心P0向5个用户Pj(j=1,2,3,4,5,)配送货物,其配送路线网络、配送中心与用户的距离以及用户的距离如下图与下表所示:图中括号内的数字表示客户的需求量(单位:吨),线路的数字表示两结点之间的距离,配送中心有(1)试利用节约里程法制定最优的配送方案;(2)设卡车行驶的速度平均为40公里/小时,试比较优化后的方案比单独向各用户分送可节约多少时间。
3、已知配送中心P0向5个用户Pj(j=1,2,3,4,5,)配送货物,其配送路线网络、配送中心与用户的距离以及用户的距离如下图与下表所示:图中括号内的数字表示客户的需求量(单位:吨),线路的数字表示两结点之间的距离,配送中心有(1)试利用节约里程法制定最优的配送方案;(2)设卡车行驶的速度平均为40公里/小时,试比较优化后的方案比单独向各用户分送可节约多少时间。
4、已知配送中心P0向5个用户Pj(j=1,2,3,4,5)配送货物,其配送路线网络、配送中心与用户的距离以及用户的距离如下图与下表所示:图中括号内的数字表示客户的需求量(单位:吨),线路的数字表示两结点之间的距离,配送中心有(1)试利用节约里程法制定最优的配送方案;(2)设卡车行驶的速度平均为40公里/小时,试比较优化后的方案比单独向各用户分送可节约多少时间。


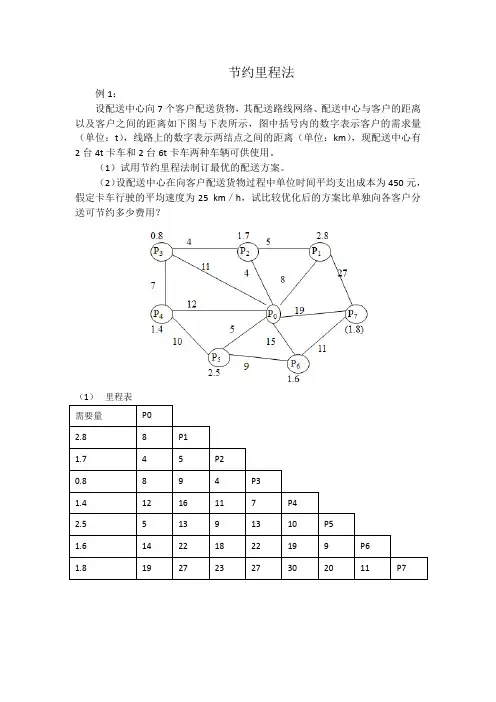
节约里程法例1:设配送中心向7个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。
(1)试用节约里程法制订最优的配送方案。
(2)设配送中心在向客户配送货物过程中单位时间平均支出成本为450元,假定卡车行驶的平均速度为25 km/h,试比较优化后的方案比单独向各客户分送可节约多少费用?(1)里程表需要量P02.8 8 P11.7 4 5 P20.8 8 9 4 P31.4 12 16 11 7 P42.5 5 13 9 13 10 P51.6 14 22 18 22 19 9 P61.8 19 27 23 27 30 20 11 P7(2)节约里程表需要量P02.8 8 P11.7 4 5(7)P20.8 8 9(7)4(8)P31.4 12 16(4)11(5)7(13)P42.5 5 13(0)9(0)13(0)10(7)P51.6 14 22(0)18(0)22(0)19(7)9(10)P61.8 19 27(0)23(0)27(0)30(1)20(4)11(22)P7(3)节约里程数排序序号路线节约里程序号路线节约里程1 P6P722 7 P4P572 P3P413 8 P1P273 P5P610 9 P2P4 54 P2P38 10 P1P4 45 P1P37 11 P5P7 46 P4P67 12 P4P7 1(4)配送路线选择节省的配送时间为节省的费用为:例2:设配送中心向5个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。


节约里程法例1:设配送中心向7个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。
(1)试用节约里程法制订最优的配送方案。
(2)设配送中心在向客户配送货物过程中单位时间平均支出成本为450元,假定卡车行驶的平均速度为25 km/h,试比较优化后的方案比单独向各客户分送可节约多少费用?(1)里程表需要量P02.8 8 P11.7 4 5 P20.8 8 9 4 P31.4 12 16 11 7 P42.5 5 13 9 13 10 P51.6 14 22 18 22 19 9 P61.8 19 27 23 27 30 20 11 P7(2)节约里程表需要量P02.8 8 P11.7 4 5(7)P20.8 8 9(7)4(8)P31.4 12 16(4)11(5)7(13)P42.5 5 13(0)9(0)13(0)10(7)P51.6 14 22(0)18(0)22(0)19(7)9(10)P61.8 19 27(0)23(0)27(0)30(1)20(4)11(22)P7(3)节约里程数排序序号路线节约里程序号路线节约里程1 P6P722 7 P4P572 P3P413 8 P1P273 P5P610 9 P2P4 54 P2P38 10 P1P4 45 P1P37 11 P5P7 46 P4P67 12 P4P7 1(4)配送路线选择节省的配送时间为节省的费用为:例2:设配送中心向5个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。

算例:节约里程法以上一个二维码扫描算法算例为例,用节约里程法计算配送线路的安排。
解:① 首先根据上一个二维码扫描算法算例中的距离矩阵表计算出各点间的节约值矩阵表,如表1所示。
表1 节约值矩阵表② 从表1中选出节约值最大值为23,其对应的两个顶点为5、6。
5、6两处的需求量之和为8,未超过一辆车的运输能力14,因此,连接5、6成回路,即0—5—6—0。
再将顶点5与6的节约值赋为0,结果如表2所示。
表2 节约矩阵表计算过程1③ 从表2中再选出节约值最大值为20,其对应的两个顶点为7、8。
7、8两处的需求量之和为7,未超过一辆车的运输能力14,因此,连接7、8成回路,即0—7—8—0。
再将顶点7与8的节约值赋为0,结果如表3所示。
表3 节约矩阵表计算过程2④ 从表3中再选出节约值最大值为16,其对应的两个顶点为5、8或6、8。
如果连接5与8,则上述两条回路合并,其总需求量为15,超过一辆车的运输能力14,因此,5与8不能连接,同样6和8也不能连接,则将顶点5、8和6、8的节约值赋为0,结果如表4所示。
表4 节约矩阵表计算过程3⑤ 从表4中再选出节约值最大值为15,其对应的两个顶点为4、6。
如连接4与6,则形成:0—5—6—4—0回路,其总需求量为11,未超过一辆车的运输能力14,因此,连接4、6成新回路,即0—5—6—4—0。
再将顶点4与6的节约值赋为0,同时,由于顶点6成为回路的中间点,则与顶点6相关的节约值都赋为0。
表示顶点6不可能再与其他点相连,其结果如表5所示。
表5-33 节约矩阵表计算过程4⑥ 按算法步骤迭代运算,直到节约值矩阵表中的值均为0时,迭代结束。
最终的结果为:0—2—3—0,0—5—6—4—0,0—7—8—1—0这三条线路,其运输量分别为9、11、13,总里程数为93。
一般来说,节约里程法可以得到比较好的结果,但此算法也是一种贪婪启发式算法,对于一些特殊的算例,得不到最优解。
上一个二维码中算例的全局最优解是:选择0—1—3—0,0—2—7—8—0,0—5—6—4—0这三条线路,其运输量分别为11、11、11,总里程数为90。

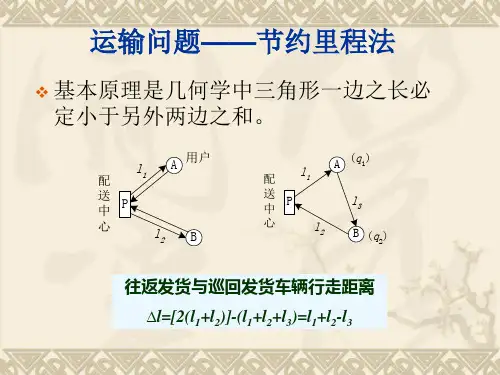
节约里程法计算公式
节约里程法的基本思想是在满足所有客户需求的前提下,通过合理规划配送路线,使得配送车辆的行驶总里程最短,从而达到节约运输成本的目的。
其核心计算公式如下:
1. 计算节约里程值(S_ij)
- 设配送中心为P,客户点i和客户点j,d_Pi表示配送中心到客户点i的距离,d_Pj表示配送中心到客户点j的距离,d_ij表示客户点i到客户点j的距离。
- 节约里程值S_ij=d_Pi+d_Pj - d_ij
例如,若配送中心P到客户点A(即i = A)的距离d_PA=10公里,配送中心P到客户点B(即j = B)的距离d_PB=12公里,客户点A到客户点B的距离d_AB=5公里,则节约里程值S_AB=d_PA+d_PB-d_AB=10 + 12-5 = 17公里。
2. 构建配送路线的步骤中的计算(以车辆载重等约束条件为例)
- 计算出所有客户点两两之间的节约里程值S_ij,并按照从大到小的顺序进行排列。
- 然后,从节约里程值最大的组合开始,判断将这两个客户点连接到同一路线是否满足车辆载重、配送时间等约束条件。
- 假设车辆的载重上限为Q,客户点i的货物需求量为q_i,客户点j的货物需求量为q_j。
如果q_i+q_j≤ Q,并且其他约束条件(如配送时间等)也满足,那么就可以将客户点i和客户点j连接到同一路线中。
- 在构建路线的过程中,不断重复这个步骤,直到所有客户点都被分配到合适的配送路线中。
节约里程法在物流配送路线规划等领域有着广泛的应用,通过合理计算节约里程值并考虑各种约束条件,可以有效地优化配送方案,提高物流配送的效率,降低物流成本。
![[计算题]节约里程法答案讲解学习](https://uimg.taocdn.com/7d22229e80eb6294dd886c78.webp)
节约里程法例1:设配送中心向7个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。
(1)试用节约里程法制订最优的配送方案。
(2)设配送中心在向客户配送货物过程中单位时间平均支出成本为450元,假定卡车行驶的平均速度为25 km/h,试比较优化后的方案比单独向各客户分送可节约多少费用?(1)作运输里程表,列出配送中心到用户及用户间的最短距离P0P1 8 P1P2 4 5 P2P3 8 9 4 P3P4 12 16 11 7 P4P5 5 13 9 13 10 P5P6 14 23 18 22 19 9 P6P7 19 27 23 27 30 20 11 P7(2)按节约里程公式求得相应的节约里程数(3)将节约里程按从大到小顺序排列表-4)根据载重量约束与节约里程大小,选择配送路线。
优先择节约里程数最大的连接点:P6-P7、P3-P4最优方案:P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0由于P6-P7是最大节约里程数连接点,所以优先选择P6-P7,又因P0-P6-P7-P1-P0路线载重量6.2t大于6t故选择P0-P7-P6-P5-P0路线5.9t(此路线选择一辆6t卡车)因P3-P4为第二大节约里程数连接点,且因路线P0-P4-P3-P2-P1-P0载重量为6.7t大于6t,故选择P0-P4-P3-P2-P0路线3.9t(此路线选择一辆4卡车)最后选P0-P1-P0路线2.8t(此路线选择一辆4卡车)得路线: P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0节约里程数=(19+14+5+12+8+4+8)*2-(19+11+9+5+12+7+4+4+8+8)=53km(53/25)*450=954元例2:设配送中心向5个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。
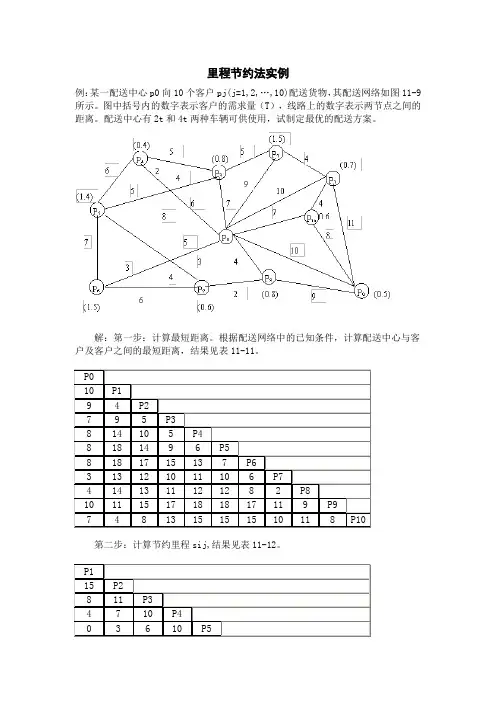
里程节约法实例例:某一配送中心p0向10个客户pj(j=1,2,…,10)配送货物,其配送网络如图11-9所示。
图中括号内的数字表示客户的需求量(T),线路上的数字表示两节点之间的距离。
配送中心有2t和4t两种车辆可供使用,试制定最优的配送方案。
解:第一步:计算最短距离。
根据配送网络中的已知条件,计算配送中心与客户及客户之间的最短距离,结果见表11-11。
第二步:计算节约里程sij,结果见表11-12。
第三步:将节约sij,进行分类,按从大到小的顺序排列,得表11-13。
表11-13???? 节约里程项目分类表第四步:确定配送线路。
从分类表中,按节约里程大小顺序,组成线路图。
(1)初始方案:对每一客户分别单独派车送货,结果如图11-10。
图11-10 初始方案初始方案:配送线路10条配送距离:S0:148km配送车辆:2t×10(2)修正方案1:按节约里程sij由大到小的顺序,连接p1和p2, p1和p10,p2和p3,得修正方案1,如图11-11。
修正方案1配送线路:10条配送距离:S1:109km配送车辆:2t×6+4t×1(3)修正方案2:在剩余的Sij中,最大的是S3,4和S4,5,此时p4和p5都有可能并入线路A中,但考虑到车辆的载重量及线路均衡问题,连接p4和p5形成一个新的线路B,得修正方案2,如图11-12。
修正方案2配送线路:6条配送距离:S2:99km配送车辆:2t×5+4t×1(4)修正方案3:接下来最大的Sij是S1,9和S5,6,由于此时p1已属于线路A,若将p9并入线路A,车辆会超载,故只将p6点并入线路B,得修正方案3,如图11-13。
图11-13 修正方案3修正方案3配送线路:5条配送距离:S3:90km配送车辆:2t×3+4t×2(5)修正方案4:再继续按Sij由大到小排出S9,10、S1,3、S2,10、S2,4、S3,6,由于与其相应的用户均已包含在已完成的线路里,故不予考虑。
节约里程法例1:设配送中心向7个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有2台4t卡车和2台6t卡车两种车辆可供使用。
(1)试用节约里程法制订最优的配送方案。
(2)设配送中心在向客户配送货物过程中单位时间平均支出成本为450元,假定卡车行驶的平均速度为25 km/h,试比较优化后的方案比单独向各客户分送可节约多少费用?(1)作运输里程表,列出配送中心到用户及用户间的最短距离P0P1 8 P1P2 4 5 P2P3 8 9 4 P3P4 12 16 11 7 P4P5 5 13 9 13 10 P5P6 14 23 18 22 19 9 P6P7 19 27 23 27 30 20 11 P7(2)按节约里程公式求得相应的节约里程数(3)将节约里程按从大到小顺序排列表-4)根据载重量约束与节约里程大小,选择配送路线。
优先择节约里程数最大的连接点:P6-P7、P3-P4最优方案:P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0由于P6-P7是最大节约里程数连接点,所以优先选择P6-P7,又因P0-P6-P7-P1-P0路线载重量6.2t大于6t故选择P0-P7-P6-P5-P0路线5.9t(此路线选择一辆6t卡车)因P3-P4为第二大节约里程数连接点,且因路线P0-P4-P3-P2-P1-P0载重量为6.7t大于6t,故选择P0-P4-P3-P2-P0路线3.9t(此路线选择一辆4卡车)最后选P0-P1-P0路线2.8t(此路线选择一辆4卡车)得路线: P0-P7-P6-P5-P0、P0-P4-P3-P2-P0、P0-P1-P0节约里程数=(19+14+5+12+8+4+8)*2-(19+11+9+5+12+7+4+4+8+8)=53km(53/25)*450=954元例2:设配送中心向5个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。
设配送中心向5个客户配送货物,其配送路线网络、配送中心与客户的距离以及客户之间的距离如下图与下表所示,图中括号内的数字表示客户的需求量(单位:t),线路上的数字表示两结点之间的距离(单位:km),现配送中心有3台2t卡车和2台4t卡车两种车辆可供使用。
(1)试用节约里程法制订最优的配送方案。
(2)假定卡车行驶的平均速度为40 km/h,试比较优化后的方案比单独向各客户分送可节约多少时间
里程表
需要量P0
8P1
812P2
6134P3
71595P4
1016181612P5
节约里程表
节约里程排序
路线选择
节约的总里程:
节省的配送时间为。