气固两相流基础理

选粉机设计实用参考资料一、气固两相流力学基础1.颗粒在静止流体内的沉降：颗粒在静止流体内自由沉降时，不仅受到重力，而且还受到浮力和阻力的作用。

在工业生产过程中，所处理的颗粒一般是比较小的，在整个降落过程基本上看着是以匀速u o进行的。

所以一般情况下，研究沉降速度问题时，是不考虑加速阶段的。

颗粒作匀速运动，降落速度u等于颗粒的沉降速度u o，计算公式为：u o={[4gd p(ρp-ρ)]/3ρξ}-2……（沉降速度计算基本公式）式中u o——球形颗粒自由沉降速度，m/s；d p——球形颗粒直径，m；g——重力加速度，m/s2；ρp————颗粒密度，kg/m3；ρ——流体密度，kg/m3；ξ——阻力系数，无因次，ξ=8/π×f(Re p),颗粒雷诺数Re p=d p u oρ/μ；μ——流体粘度，Pa.s。

当Re p＜1时，流体属层流时，则得：u o=[d p2(ρp-ρ)g]/18μ此式适用于层流时球形颗粒的自由沉降速度计算，称为斯托克斯（Stokes）公式；当1＜Re p＜10000时，流体属过渡流时，则得：u o=0.2{[(ρp-ρ)/ρ]g}0.73×d p1.18/ (μ/ρ)0.45此式适用于过渡流时球形颗粒的自由沉降速度计算，称为阿纶（Allen）公当10000＜Re p＜2×105时，流体属踹流时，则得：u o=1.74{[(ρp-ρ)/ρ]g}0.5×d p0.5此式适用于踹流时球形颗粒的自由沉降速度计算，称为牛顿（Newton）公式。

颗粒在静止流体内的沉降速度计算实例：例1：求直径为30μm的球形石英颗粒，在20℃的空气中的沉降速度，石英颗粒的密度为2650kg/cm3。

解：标准状态下空气的密度为 1.293kg/cm3。

故20℃时，空气的密度为ρ=1.293×[273/(273+20)]=1.205 kg/cm3。

而粘度为0.0185×10-3Pa.s。

第三章循环流化床锅炉气固两相流基础理论循环流化床锅炉中的气—固两相流流体动力特性是学习其燃烧特性和传热特性的基础。

为了叙述方便和更好地理解本章及以后章节的内容，首先简单介绍一下循环流化床锅炉涉及的部分概念和定义。

第三节流化床基本原理一、颗粒流态化的概念1．流态化现象当气体或液体以一定的速度向上流过固体颗粒层时，固体颗粒层呈现出类似于液体状态的现象，称为流化现象。

2．流态化的定义当气体或液体以一定的速度流过固体颗粒层，并且气体或液体对固体颗粒产生的作用力与固体颗粒所受的其他外力相平衡时，固体颗粒层呈现出类似于液体状态的现象或者当固体颗粒与气体或液体接触时固体颗粒转变成类似流体状态，这种状态称为流态化。

3．流化床的流体力学性质流化床流态化后，具有与流体一样的性能，主要表现在以下几方面。

（1）浮力定律。

密度小于流体密度的物体会浮在床层表面上。

（2）液面特性。

床表面保持水平，形状保持容器的形状。

（3）小孔射流。

在流化床侧面开孔，流化床固体物料像流体一样射流，离床层上表面越近，射流距离越小；越靠近流化床底部，射流距离越大，也可以从底部流出去。

（4）连通效应。

几个流化床底部联通后，床层高度自动保持同一水平高度。

气体流化床的拟流体性质见图3—4图3—4 气体流化床的拟流体性质气固流化床类似流体的性质还有：①在任一高度的静压近似于在此高度以上单位床截面内固体颗粒的重要；②密度高于床层表面密度的物体在床内会下沉，密度小于床层表面密度的物体会浮在床面上；③床内颗粒混合良好，因此，当加热床层时，整个床层的温度基本均匀。

一般的液—固流态化，颗粒均匀地分散于床层中，称之为“散式”流态化。

而一般的气—固流态化，气体并不均匀地流过颗粒床层，一部分气体形成汽包经床层短路逸出，颗粒则被分成群体做湍流运动，床层中的空隙率随位置和时间的不同而变化，因此这种流态化称为“聚式”流态化。

燃煤循环流化床锅炉靠空气或烟气流化颗粒状物料，属气—固流态化范畴，也即属于聚式流态化。

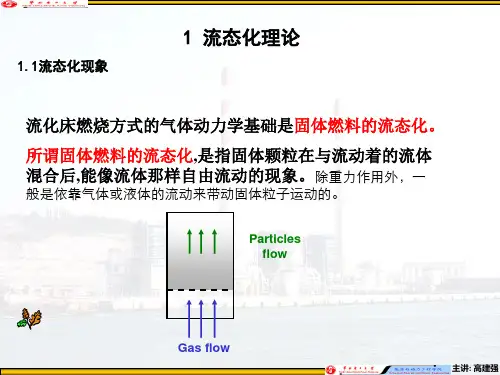
1 流态化理论1.1流态化现象流化床燃烧方式的气体动力学基础是固体燃料的流态化。

所谓固体燃料的流态化,是指固体颗粒在与流动着的流体混合后,能像流体那样自由流动的现象。

除重力作用外，一般是依靠气体或液体的流动来带动固体粒子运动的。

ParticlesflowGas flow1 流态化理论1.1 流态化现象•流态化用来描述固体颗粒与流体接触的某种运动形态。

❿气体达到能将颗粒悬浮的速度，颗粒彼此之间分离，颗粒在任何方向上运动和转动。

❿与高粘度液体性质相似。

1.1流态化现象ParticlesflowGas flow1 流态化理论1.2流态化的描述及其性质⏹散式流化和聚式流化➢散式流化d b /dp＜1d b ——气泡直径dp——颗粒直径对于L-S系统，流体与粒子的密度相差不大，故umf 一般很小，流速进一步提高时，床层膨胀均匀且波动很小，粒子在床内的分布也比较均匀，故称作散式流化态。

颗粒越细，流体与固体的△ρ值越小，则越接近理想流化，流化质量也就越好。

1.2流态化的描述及其性质➢聚式流化d b /dp＞10对于G-S系统，一般在气速超过Umf后，将会出现气泡，气速越高，气泡造成的扰动也越剧烈，使床层波动频繁，这种形态的流化床称聚式流化床。

处于流化状态的颗粒系统称为流化床当气体通过布风板自下而上地穿过固体颗粒随意填充状态的床层时，整体床层将依气体流速的不断增大而呈现完全不同的状态。

1.2流态化的描述及其性质1.2流态化的描述及其性质总结：固定床：固体粒子处于堆紧状态，颗粒静止不动的床层，叫做固定床。

床层的压降随流体流速的增加而增加。

移动床：流体和固体颗粒同时进入反应器，他们互相接触，一面进行反应，一面颗粒移动。

流化床：床层颗粒之间脱离接触，颗粒悬浮在流体中，往各个方向运动的床层叫做流化床。

床层高度和空隙率随流速增大而增大，但床层压降基本不随流速而变。

散式流化床：固体颗粒脱离接触，但颗粒分布均匀，颗粒间充满流体，无颗粒与流体的聚集状态，此时已具有一些流体性能。

气固两相流体力学模型在燃煤发电中的应用引言燃煤发电是目前世界各国主要的电力供应方式之一。

然而，燃煤发电过程中产生的煤烟气排放对环境和人体健康带来了巨大的挑战。

为了更好地理解燃煤发电过程中的气固两相流体行为，研究人员对气固两相流体力学模型进行了广泛的应用。

本文将介绍气固两相流体力学模型在燃煤发电中的应用及其意义。

气固两相流体力学模型的基本原理气固两相流体力学模型是研究气固两相流体行为的基本工具之一。

它基于流体动力学方程和颗粒运动方程，描述了气相和固相在空间和时间上的运动规律。

常用的气固两相流体力学模型包括欧拉-拉格朗日方法、欧拉-欧拉方法和多尺度方法等。

欧拉-拉格朗日方法将气相和固相视为两个不同的相，分别采用欧拉方法和拉格朗日方法描述其运动。

其中，欧拉方法假设气相和固相是均匀连续的流体，通过质量守恒、动量守恒和能量守恒方程描述其运动；拉格朗日方法则将固相中的颗粒视为相互独立的个体，通过颗粒的运动方程描述其运动。

欧拉-欧拉方法将气相和固相都视为均匀连续的流体，通过质量守恒、动量守恒和能量守恒方程描述其运动。

多尺度方法则将气相和固相的微观和宏观尺度结合起来，通过不同的尺度转换关系建立它们之间的联系。

燃煤发电中的气固两相流体力学模型应用煤燃烧过程中的气固两相流体行为研究煤燃烧是燃煤发电中最主要的过程之一，其燃烧特性对发电效率和煤炭利用率有着重要影响。

通过气固两相流体力学模型，研究人员可以深入分析煤燃烧过程中气相中的燃烧反应、物质传输和能量转化等过程，以及固相中的煤炭颗粒的燃烧和热解过程。

粉煤灰颗粒在燃煤发电中的传输和分离研究在燃煤发电过程中，粉煤灰是煤燃烧产生的主要固体产物之一。

通过气固两相流体力学模型，研究人员可以模拟粉煤灰颗粒在烟气中的传输和分离过程。

这对于合理设计燃煤发电厂的除尘设备以及减少粉煤灰排放具有重要意义。

气固两相流体行为对燃烧控制和污染物排放的影响研究气固两相流体力学模型还可以用于研究气相和固相之间的相互作用对燃烧过程和污染物排放的影响。

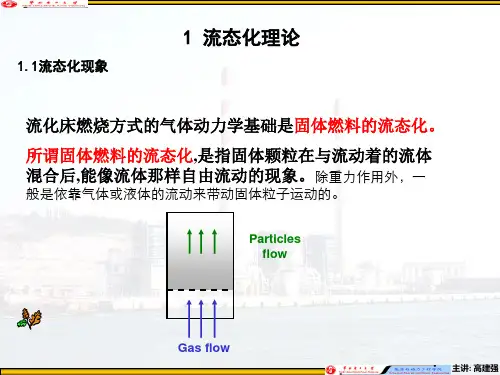
1 流态化理论1.1流态化现象流化床燃烧方式的气体动力学基础是固体燃料的流态化。

所谓固体燃料的流态化,是指固体颗粒在与流动着的流体混合后,能像流体那样自由流动的现象。

除重力作用外，一般是依靠气体或液体的流动来带动固体粒子运动的。

ParticlesflowGas flow1 流态化理论1.1 流态化现象•流态化用来描述固体颗粒与流体接触的某种运动形态。

•气体达到能将颗粒悬浮的速度，颗粒彼此之间分离，颗粒在任何方向上运动和转动。

•与高粘度液体性质相似。

1.1 流态化现象Particlesflow Gas flow1 流态化理论1.2流态化的描述及其性质⏹散式流化和聚式流化 散式流化db /dp＜1db ——气泡直径 dp——颗粒直径对于L-S系统，流体与粒子的密度相差不大，故umf 一般很小，流速进一步提高时，床层膨胀均匀且波动很小，粒子在床内的分布也比较均匀，故称作散式流化态。

颗粒越细，流体与固体的△ρ值越小，则越接近理想流化，流化质量也就越好。

1.2流态化的描述及其性质 聚式流化d b /dp＞10对于G-S系统，一般在气速超过Umf后，将会出现气泡，气速越高，气泡造成的扰动也越剧烈，使床层波动频繁，这种形态的流化床称聚式流化床。

处于流化状态的颗粒系统称为流化床当气体通过布风板自下而上地穿过固体颗粒随意填充状态的床层时，整体床层将依气体流速的不断增大而呈现完全不同的状态。

1.2流态化的描述及其性质1.2流态化的描述及其性质总结：固定床：固体粒子处于堆紧状态，颗粒静止不动的床层，叫做固定床。

床层的压降随流体流速的增加而增加。

移动床：流体和固体颗粒同时进入反应器，他们互相接触，一面进行反应，一面颗粒移动。

流化床：床层颗粒之间脱离接触，颗粒悬浮在流体中，往各个方向运动的床层叫做流化床。

床层高度和空隙率随流速增大而增大，但床层压降基本不随流速而变。

散式流化床：固体颗粒脱离接触，但颗粒分布均匀，颗粒间充满流体，无颗粒与流体的聚集状态，此时已具有一些流体性能。

1 流态化理论1.1流态化现象流化床燃烧方式的气体动力学基础是固体燃料的流态化。

所谓固体燃料的流态化,是指固体颗粒在与流动着的流体混合后,能像流体那样自由流动的现象。

除重力作用外，一般是依靠气体或液体的流动来带动固体粒子运动的。

ParticlesflowGas flow1 流态化理论1.1 流态化现象•流态化用来描述固体颗粒与流体接触的某种运动形态。

•气体达到能将颗粒悬浮的速度，颗粒彼此之间分离，颗粒在任何方向上运动和转动。

•与高粘度液体性质相似。

1.1流态化现象ParticlesflowGas flow1 流态化理论1.2流态化的描述及其性质⏹散式流化和聚式流化 散式流化d b /dp＜1d b ——气泡直径dp——颗粒直径对于L-S系统，流体与粒子的密度相差不大，故umf 一般很小，流速进一步提高时，床层膨胀均匀且波动很小，粒子在床内的分布也比较均匀，故称作散式流化态。

颗粒越细，流体与固体的△ρ值越小，则越接近理想流化，流化质量也就越好。

1.2流态化的描述及其性质 聚式流化d b /dp＞10对于G-S系统，一般在气速超过Umf后，将会出现气泡，气速越高，气泡造成的扰动也越剧烈，使床层波动频繁，这种形态的流化床称聚式流化床。

处于流化状态的颗粒系统称为流化床当气体通过布风板自下而上地穿过固体颗粒随意填充状态的床层时，整体床层将依气体流速的不断增大而呈现完全不同的状态。

1.2流态化的描述及其性质1.2流态化的描述及其性质总结：固定床：固体粒子处于堆紧状态，颗粒静止不动的床层，叫做固定床。

床层的压降随流体流速的增加而增加。

移动床：流体和固体颗粒同时进入反应器，他们互相接触，一面进行反应，一面颗粒移动。

流化床：床层颗粒之间脱离接触，颗粒悬浮在流体中，往各个方向运动的床层叫做流化床。

床层高度和空隙率随流速增大而增大，但床层压降基本不随流速而变。

散式流化床：固体颗粒脱离接触，但颗粒分布均匀，颗粒间充满流体，无颗粒与流体的聚集状态，此时已具有一些流体性能。

第2章气固两相流理论分析气固两相流是指同时存在气体和固体颗粒的流动现象。

在很多工程和科学领域中，气固两相流的研究具有重要意义。

本文将对气固两相流的理论分析进行讨论。

首先，我们需要了解气固两相流的基本特征。

在气固两相流中，气体相和固体相之间存在着相互作用力。

这些力可以分为两类：牵引力和阻力。

牵引力是气体对固体颗粒施加的力，使其发生运动。

阻力则是固体颗粒对气体施加的力，使其受到阻碍。

然后，我们可以利用流体力学的基本原理来进行气固两相流的分析。

首先，我们需要根据质量守恒定律来描述气体相和固体相的质量流动。

然后，我们可以利用动量守恒定律来描述气体相和固体相的力学行为。

最后，我们可以利用能量守恒定律来描述气体相和固体相的能量变化。

在进行具体的气固两相流理论分析时，我们需要考虑一些重要参数。

首先是气体相和固体相的体积分数，即气体相和固体相在混合物中的比例。

其次是气体相和固体相的速度分布，即气体相和固体相在流动中的速度分布情况。

另外，我们还需要考虑气体相和固体相之间的相互作用力和阻力，以及颗粒之间的碰撞情况。

在进行气固两相流的理论分析时，我们可以将其分为几个研究方向。

首先是气固两相流的基本理论研究，包括气固两相流的基本方程和重要参数的推导和解析解。

其次是气固两相流的数值模拟研究，包括使用数值方法对气固两相流进行模拟和预测。

最后是气固两相流的实验研究，包括设计实验装置和进行实验观测。

总之，气固两相流的理论分析是一个复杂且重要的研究领域。

通过对气固两相流的理论分析，我们可以深入了解气固两相流的特性和行为，并为相关工程和科学领域的应用提供理论支持。

通过不断深入研究，我们可以进一步完善气固两相流的理论模型和分析方法，以满足实际应用的需求。