同济大学钢结构基本原理第八章课后习题答案2

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图（a ）理想弹性－塑性 （b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化） （2）弹性阶段：tan E σεαε==⋅非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm =2270/c N mm σ=0.025F ε=522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610y f E ε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-= （2）B 点：卸载前应变：0.025F εε==卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-= （3）C 点：卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

第二章如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

图2-34 σε-图（a ）理想弹性－塑性 （b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅非弹性阶段：'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？ 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610yf E ε===⨯卸载后残余应变：0c ε= 可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f E εε=-= 可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变：0.05869c c E σεε=-= 可恢复弹性应变：0.00131y c εεε=-=试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

第二章如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

图2-34 σε-图（a ）理想弹性－塑性 （b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅非弹性阶段：'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？ 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610yf E ε===⨯卸载后残余应变：0c ε= 可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f E εε=-= 可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变：0.05869c c E σεε=-= 可恢复弹性应变：0.00131y c εεε=-=试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

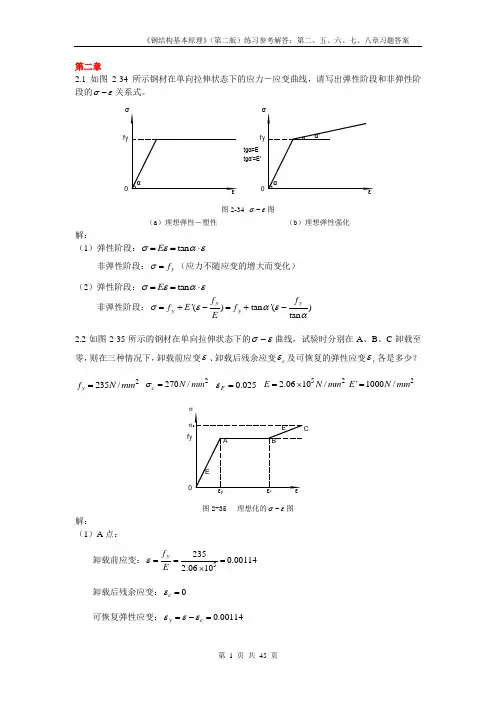
第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化） （2）弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点： 卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

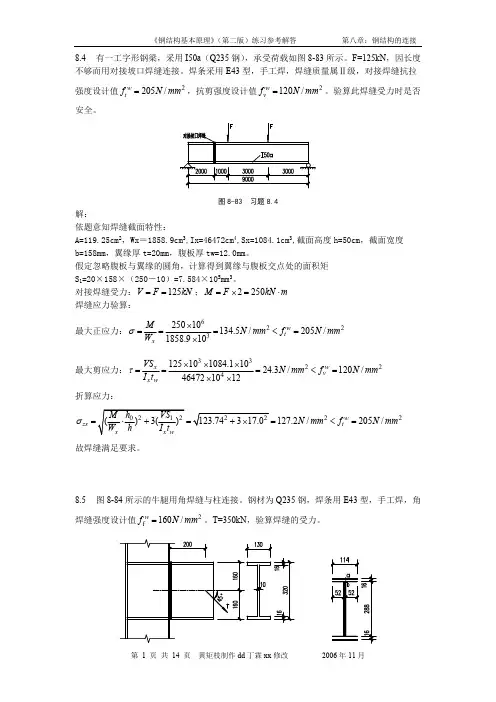
nt8.4 有一工字形钢梁，采用I50a （Q235钢），承受荷载如图8-83所示。

F=125kN ，因长度不够而用对接坡口焊缝连接。

焊条采用E43型，手工焊，焊缝质量属Ⅱ级，对接焊缝抗拉强度设计值，抗剪强度设计值。

验算此焊缝受力时是否2205/w t f N mm =2120/w v f N mm =安全。

解：依题意知焊缝截面特性：A=119.25cm 2，Wx ＝1858.9cm 3,Ix=46472cm 4,Sx=1084.1cm 3,截面高度h=50cm ，截面宽度b=158mm ，翼缘厚t=20mm ，腹板厚tw=12.0mm 。

假定忽略腹板与翼缘的圆角，计算得到翼缘与腹板交点处的面积矩S 1=20×158×（250－10）=7.584×105mm 3。

对接焊缝受力：；125V F kN ==2250M F kN m =⨯=⋅焊缝应力验算：最大正应力：622325010134.5/205/1858.910w tx M N mm f N mm W σ⨯===<=⨯最大剪应力：33224125101084.11024.3/120/464721012w x v x w VS N mm f N mm I t τ⨯⨯⨯===<=⨯⨯折算应力：22127.2/205/w zs t N mm f N mm σ===<=故焊缝满足要求。

8.5 图8-84所示的牛腿用角焊缝与柱连接。

钢材为Q235钢，焊条用E43型，手工焊，角焊缝强度设计值。

T=350kN ，验算焊缝的受力。

2f 160/w f N mm =图8-84 习题8.5 图8-84-1 焊缝截面计算简图解：（注：焊缝上下翼缘长度114mm有些问题，应取，黄钜枝06年6月192130210110l t mm-=-⨯=日）此注错误，应取消。

罗烈08年10月28日如图8-84-1，截面特性计算如下：2(11425242882)0.75667.2fA h mm=⨯+⨯+⨯⨯=228820.73225.6w fA h mm=⨯⨯=3274 1288288[2882114(16)252()4]0.77.913101222f fI h mm=⨯⨯+⨯+⨯+⨯⨯⨯=⨯焊缝受力：；；247.5N kN==247.5V kN=49.5M V e kN m=⋅=⋅应力验算：危险点为a、b两点，下面分别验算：对a点：32247.51043.67/5667.2NaNN mmAσ⨯===62749.510160100.09/7.91310M aafMyN mmIσ⨯⨯===⨯2243.67100.09143.76/195.2/N M wa a f fN mm f N mmσσβ+=+=<=对b点：32247.51076.73/3225.6VbwVN mmAτ⨯===243.67/N Nb aN mmσσ==62749.51014490.16/7.91310M bbfMyN mmIσ⨯⨯===⨯22133.87/160/wfN mm f N mm==<=故焊缝强度满足要求。

同济大学钢结构基本原理(沈祖炎)课后习题答案完全版第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f 0f 0tgα=E 图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化） （2）弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f 0σF图2-35 理想化的σε-图解：（1）A 点：卸载前应变：2350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点： 卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

钢结构基本原理课后习题与答案完全版2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f y 0f y 0tgα=E图2-34 σε-图（a ）理想弹性－塑性 （b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅非弹性阶段：'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f y 0σF图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610y f E ε===⨯卸载后残余应变：0c ε= 可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f E εε=-= 可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变：0.05869c c E σεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

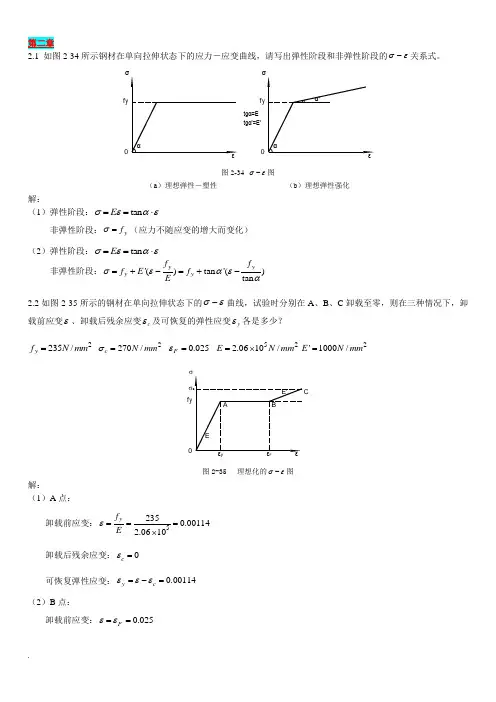
2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化） （2）弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσ图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε==卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点： 卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

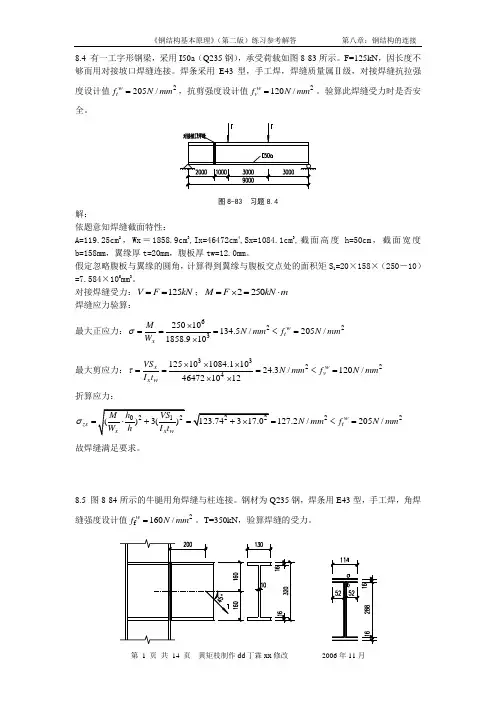
8.4 有一工字形钢梁，采用I50a （Q235钢），承受荷载如图8-83所示。

F=125kN ，因长度不够而用对接坡口焊缝连接。

焊条采用E43型，手工焊，焊缝质量属Ⅱ级，对接焊缝抗拉强度设计值2205/w t f N mm =，抗剪强度设计值2120/w v f N mm =。

验算此焊缝受力时是否安全。

图8-83 习题8.4解：依题意知焊缝截面特性：A=119.25cm 2，Wx ＝1858.9cm 3,Ix=46472cm 4,Sx=1084.1cm 3,截面高度h=50cm ，截面宽度b=158mm ，翼缘厚t=20mm ，腹板厚tw=12.0mm 。

假定忽略腹板与翼缘的圆角，计算得到翼缘与腹板交点处的面积矩S 1=20×158×（250－10）=7.584×105mm 3。

对接焊缝受力：125V F kN ==；2250M F kN m =⨯=⋅ 焊缝应力验算：最大正应力：622325010134.5/205/1858.910w t x M N mm f N mm W σ⨯===<=⨯ 最大剪应力：33224125101084.11024.3/120/464721012w x v x w VS N mm f N mm I t τ⨯⨯⨯===<=⨯⨯ 折算应力：22127.2/205/w zs t N mm f N mm σ=<= 故焊缝满足要求。

8.5 图8-84所示的牛腿用角焊缝与柱连接。

钢材为Q235钢，焊条用E43型，手工焊，角焊缝强度设计值2f 160/w f N mm =。

T=350kN ，验算焊缝的受力。

图8-84 习题8.5 图8-84-1 焊缝截面计算简图解：（注：焊缝上下翼缘长度114mm 有些问题，应取2130210110l t mm -=-⨯=，黄钜枝06年6月19日）此注错误，应取消。

罗烈08年10月28日如图8-84-1，截面特性计算如下：2(11425242882)0.75667.2f A h mm =⨯+⨯+⨯⨯= 228820.73225.6w f A h mm =⨯⨯=32741288288[2882114(16)252()4]0.77.913101222f f I h mm =⨯⨯+⨯+⨯+⨯⨯⨯=⨯焊缝受力：247.5N kN =；247.5V kN =； 49.5M V e kN m =⋅=⋅ 应力验算：危险点为a 、b 两点，下面分别验算： 对a 点： 32247.51043.67/5667.2N aN N mm A σ⨯===62749.510160100.09/7.91310M a af My N mm I σ⨯⨯===⨯ 2243.67100.09143.76/195.2/N Mw a a f f N mm f N mm σσβ+=+=<=对b 点：32247.51076.73/3225.6V bw V N mm A τ⨯=== 243.67/N Nb a N mm σσ==62749.51014490.16/7.91310M b bf My N mm I σ⨯⨯===⨯22133.87/160/w f N mm f N mm =<=故焊缝强度满足要求。

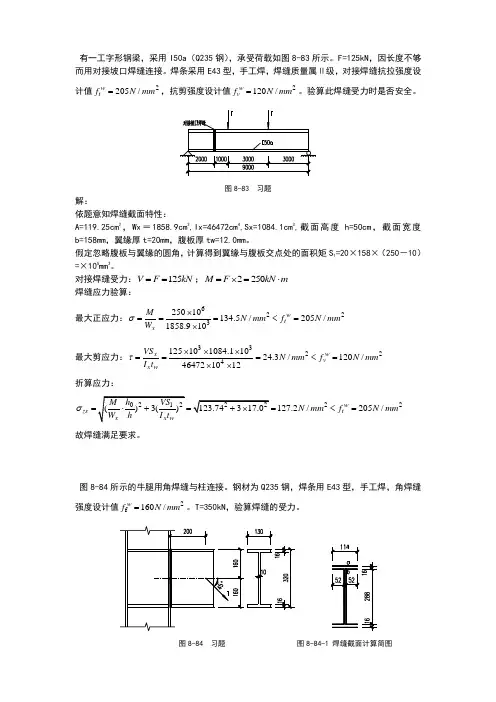
有一工字形钢梁，采用I50a （Q235钢），承受荷载如图8-83所示。

F=125kN ，因长度不够而用对接坡口焊缝连接。

焊条采用E43型，手工焊，焊缝质量属Ⅱ级，对接焊缝抗拉强度设计值2205/w t f N mm =，抗剪强度设计值2120/w v f N mm =。

验算此焊缝受力时是否安全。

图8-83 习题解：依题意知焊缝截面特性：A=119.25cm 2，Wx ＝1858.9cm 3,Ix=46472cm 4,Sx=1084.1cm 3,截面高度h=50cm ，截面宽度b=158mm ，翼缘厚t=20mm ，腹板厚tw=12.0mm 。

假定忽略腹板与翼缘的圆角，计算得到翼缘与腹板交点处的面积矩S 1=20×158×（250－10）=×105mm 3。

对接焊缝受力：125V F kN ==；2250M F kN m =⨯=⋅ 焊缝应力验算：最大正应力：622325010134.5/205/1858.910w t x M N mm f N mm W σ⨯===<=⨯ 最大剪应力：33224125101084.11024.3/120/464721012w x v x w VS N mm f N mm I t τ⨯⨯⨯===<=⨯⨯ 折算应力：22127.2/205/w zs t N mm f N mm σ=<= 故焊缝满足要求。

图8-84所示的牛腿用角焊缝与柱连接。

钢材为Q235钢，焊条用E43型，手工焊，角焊缝强度设计值2f 160/w f N mm =。

T=350kN ，验算焊缝的受力。

图8-84 习题 图8-84-1 焊缝截面计算简图解：（注：焊缝上下翼缘长度114mm 有些问题，应取2130210110l t mm -=-⨯=，黄钜枝06年6月19日）此注错误，应取消。

罗烈08年10月28日如图8-84-1，截面特性计算如下：2(11425242882)0.75667.2f A h mm =⨯+⨯+⨯⨯= 228820.73225.6w f A h mm =⨯⨯=32741288288[2882114(16)252()4]0.77.913101222f f I h mm =⨯⨯+⨯+⨯+⨯⨯⨯=⨯焊缝受力：247.52N kN ==；247.52V kN ==； 49.5M V e kN m =⋅=⋅ 应力验算：危险点为a 、b 两点，下面分别验算： 对a 点： 32247.51043.67/5667.2N aN N mm A σ⨯===62749.510160100.09/7.91310M a af My N mm I σ⨯⨯===⨯ 2243.67100.09143.76/195.2/N Mw a a f f N mm f N mm σσβ+=+=<=对b 点：32247.51076.73/3225.6V bw V N mm A τ⨯=== 243.67/N Nb a N mm σσ==62749.51014490.16/7.91310M b bf My N mm I σ⨯⨯===⨯22133.87/160/w f N mm f N mm =<=故焊缝强度满足要求。

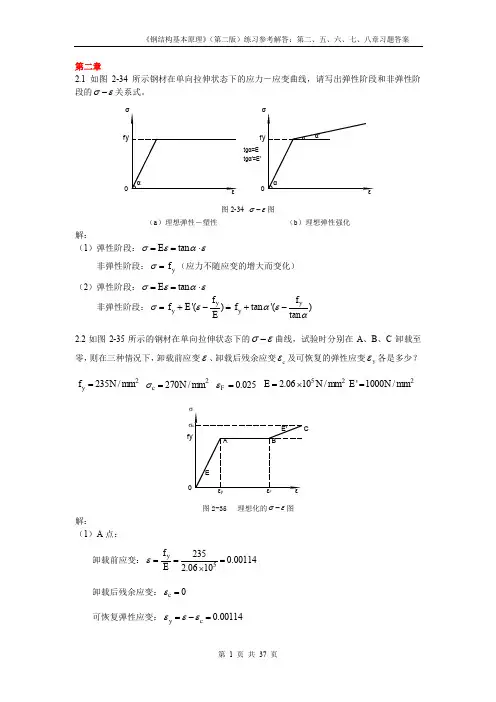
第二章2.1如图2-34所示钢材在单向拉伸状态下的应力一应变曲线，请写出弹性阶段和非弹性阶 段的 关系式。

解：（1）弹性阶段：E tan非弹性阶段：f y （应力不随应变的增大而变化）（2）弹性阶段：E tanf yf y 非弹性阶段：f y E'（ 丄）f y tan '（ 匚）Etan卸载后残余应变： c 0可恢复弹性应变:(2) B 点:（b ）理想弹性强化2.2如图2-35所示的钢材在单向拉伸状态下的曲线，试验时分别在 A 、B 、C 卸载至零,则在三种情况下，卸载前应变、卸载后残余应变 c 及可恢复的弹性应变y 各是多少?2f y 235N/mm 22c270 N / mm 2F 0.025 E 2.06 105N/mm 2 E' 1000N/mm 2解：（1）A 点：卸载前应f yE235 2.06 1050.001140.00114图图2-35 理想化的 图卸载前应变：F0.025卸载后残余应变：c0.02386E可恢复弹性应变：y c0.00114(3) C点：c fy卸载前应变：F0.025 0.035 0.06 E'卸载后残余应变：c c0.05869 E可恢复弹性应变：y c0.001312.3试述钢材在单轴反复应力作用下，钢材的曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材曲线与反复应力大小和作用时间关系：当构件反复力| | fy时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材曲线基本无变化；当I I fy时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载-卸载连续进行，钢材曲线也基本无变化；若加载-卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

钢材曲线会相对更高而更短。

另外，载一定作用力下，作用时间越快，钢材强度会提高、而变形能力减弱，钢材曲线也会更高而更短。

第二章如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图（a ）理想弹性－塑性 （b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化） （2）弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =σf yCσF图2-35 理想化的σε-图 解： （1）A 点： 卸载前应变：52350.001142.0610y f E ε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=（2）B 点： 卸载前应变：0.025Fεε==卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点： 卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

第二章 钢结构材料2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f 0f 0tgα=E 图2-34 σε-图（a ）理想弹性－塑性 （b ）理想弹性强化解：由题意得：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化） （2）弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f 0σF图2-35 理想化的σε-图解：分三种情况： （1）A 点：卸载前应变：52350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=（2）B 点： 卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点： 卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f y0f y 0tgα=E图2-34 σε-图（a ）理想弹性－塑性 （b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅非弹性阶段：'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610yf E ε===⨯卸载后残余应变：0c ε= 可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f E εε=-= 可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变：0.05869cc E σεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。