全国名校高中数学优质试题(附详解)高一数学第一次月考试题及答案

高一上学期第一次月考数学试卷（含答案解析）考试时间：120分钟；总分：150分学校:___________姓名：___________班级：___________考号：___________第I 卷（选择题）一、单选题（本大题共8小题，共40.0分。

在每小题列出的选项中，选出符合题目的一项）1. 若集合A ={x|x >2}，B ={x|−2⩽x ⩽3}，则A ∩B =( )A. (2,3)B. (2,3]C. [2,3]D. [−2,3]2. 如图所示的Venn 图中，已知A ，B 是非空集合，定义A ∗B 表示阴影部分的集合.若A ={x |0≤x <3}，B ={y |y >2}，则A ∗B =( )A. {x |x >3}B. {x |2≤x ≤3}C. {x |2<x <3}D. {x |x ≥3}3. 中国清朝数学家李善兰在859年翻译《代数学》中首次将“function ”译做“函数”，沿用至今.为什么这么翻译，书中解释说“凡此变数中函彼变数者，则此为彼之函数.”这个解释说明了函数的内涵：只要有一个法则，使得取值范围中的每一个值x ，有一个确定的y 和它对应就行了，不管这个对应的法则是公式、图象、表格还是其它形式.已知函数f(x)由如表给出，则f(f(−2)+1)的值为( )A. 1B. 2C. 3D. 44. 命题“∀x >1，x −1>lnx ”的否定为( )A. ∀x ≤1，x −1≤lnxB. ∀x >1，x −1≤lnxC. ∃x ≤1，x −1≤lnxD. ∃x >1，x −1≤lnx5. 设M =2a(a −2)+7，N =(a −2)(a −3)，则M 与N 的大小关系是( )A. M >NB. M =NC. M <ND. 无法确定6. f(2x −1)的定义域为[0,1)，则f(1−3x)的定义域为( )A. (−2,4]B. (−2,12]C. (0,23]D. (0,16] 7. 已知x ∈R ，则“(x −2)(x −3)≤0成立”是“|x −2|+|x −3|=1成立”的条件．( )A. 充分不必要B. 必要不充分C. 充分必要D. 既不充分也不必要 8. 已知集合A ={x|3−x x ≥2)}，则∁R A =( ) A. {x|x >1}B. {x|x ≤0或x >1}C. {x|0<x <1}D. {x|x <0或x >1}二、多选题（本大题共4小题，共20.0分。

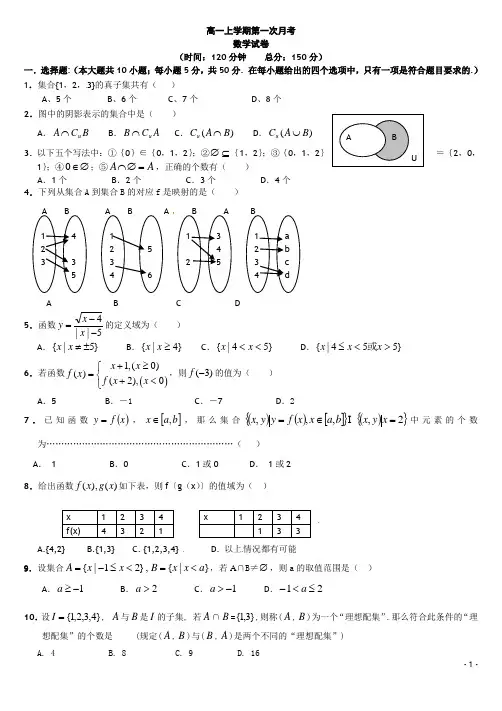
高一上学期第一次月考数学试卷（时间：120分钟 总分：150分）一．选择题:（本大题共10小题；每小题5分，共50分. 在每小题给出的四个选项中，只有一项是符合题目要求的.） 1．集合{1，2，3}的真子集共有（ ）A 、5个B 、6个C 、7个D 、8个 2．图中的阴影表示的集合中是（ ）A ．BC A u ⋂ B ．A C B u ⋂ C ．)(B A C u ⋂D ．)(B A C u ⋃ ｛2，0，1｝；3. 以下五个写法中：①｛0｝∈｛0，1，2｝；②⊆∅｛1，2｝；③｛0，1，2｝＝④∅∈0；⑤A A =∅⋂，正确的个数有（ ）A ．1个B ．2个C ．3个D ．4个 4．下列从集合A 到集合B 的对应f 是映射的是（ ）A B C D5．函数5||4--=x x y 的定义域为（ ）A ．}5|{±≠x xB ．}4|{≥x xC ．}54|{<<x xD ．}554|{><≤x x x 或6．若函数()1,(0)()(2),0x x f x f x x +≥⎧=⎨+<⎩，则)3(-f 的值为（ ）A ．5B ．－1C ．－7D ．2 7．已知函数()x f y =，[]b a x ,∈，那么集合()()[]{}(){}2,,,,=∈=x y x b a x x f y y x 中元素的个数为………………………………………………………（ ） A ． 1 B ．0 C ．1或0 D ． 1或2 8．给出函数)(),(x g x f 如下表，则f 〔g （x ）〕的值域为（ ）A.{4,2}B.{1,3}C. {1,2,3,4}D. 以上情况都有可能9．设集合}|{,}21|{a x x B x x A <=<≤-=，若A ∩B ≠∅，则a 的取值范围是（ ）A ．1-≥aB ．2>aC ．1->aD ．21≤<-a10．设}4,3,2,1{=I , A 与B 是I 的子集, 若A ∩B =}3,1{,则称(A ,B )为一个“理想配集”.那么符合此条件的“理想配集”的个数是 (规定(A ,B )与(B ,A )是两个不同的“理想配集”)A. 4B. 8C. 9D. 16 二．填空题（本大题共5个小题，每小题４分，共20分）11．已知集合{}12|),(-==x y y x A ，}3|),{(+==x y y x B 则A B ＝ 12．若函数1)1(2-=+x x f ，则)2(f ＝_____ __ _____13．若函数)(x f 的定义域为[－1，2]，则函数)23(x f -的定义域是 14．函数2()2(1)2f x x a x =+-+在区间(,4]-∞上递减，则实数a 的取值范围是____ __15．对于函数()y f x =，定义域为]2,2[-=D ，以下命题正确的是（只要求写出命题的序号） ①若(1)(1),(2)(2)f f f f -=-=，则()y f x =是D 上的偶函数；②若对于]2,2[-∈x ，都有0)()(=+-x f x f ，则()y f x =是D 上的奇函数； ③若函数)(x f y =在D 上具有单调性且)1()0(f f >则()y f x =是D 上的递减函数； ④若(1)(0)(1)(2)f f f f -<<<，则()y f x =是D 上的递增函数。

高一数学必修1第一次月考试卷(含答案解析)高一数学必修1第一次月考试卷(含答案解析)一、选择题1. 若集合A={2,4,6,8}，集合B={1,3,5,7}，则A∪B=（）A. {1, 2, 3, 4, 5, 6, 7, 8}B. {1, 2, 3, 4, 5, 6, 7}C. {2, 4, 6, 8}D. {1, 3, 5, 7}解析：集合的并就是包含所有元素的集合，所以A∪B={1, 2, 3, 4, 5, 6, 7, 8}，选项A正确。

2. 已知二次函数y=ax²+bx+c的顶点坐标为（1，2），则a+b+c的值为（）A. 3B. 4C. 5D. 6解析：二次函数的顶点坐标为（h，k），所以a+b+c=a(h²)+b(h)+c=a(1²)+b(1)+c=a+b+c=k=2，选项B正确。

3. 若点P(3,4)在直线5x-ky=3上，则k的值为（）A. 1B. 2C. 3D. 4解析：点P(3,4)在直线5x-ky=3上，代入坐标得到5(3)-k(4)=3，化简得15-4k=3，解得k=3，选项C正确。

二、填空题4. 根据等差数列的通项公式an=a1+(n-1)d，已知a1=3，a4=9，求公差d为_____。

解析：代入已知条件，9=3+(4-1)d，化简得3=3d，解得d=1。

公差d为1。

5. 在△ABC中，∠A=60°，BC=8，AB=4，则∠B=_____。

解析：根据三角形内角和为180°，∠B+60°+∠C=180°，化简得∠B+∠C=120°。

由已知BC=8，AB=4，利用正弦定理sinB=BC/AB=8/4=2，所以∠B=30°。

三、解答题6. 已知集合A={x|2x+1<5}，求A的解集。

解析：将不等式2x+1<5移项得到2x<4，再除以2得到x<2。

所以集合A的解集为{x|x<2}。

河南省名校联考2024-2025学年高一上学期第一次月考数学试卷学校：___________姓名：___________班级：___________考号：___________一、选择题1．下列关系式正确的是( )B. C. D.2．关于命题A.q 是存在量词命题,是真命题B.q 是存在量词命题,是假命题C.q 是全称量词命题,是真命题D.q 是全称量词命题,是假命题3．已知集合,则用列举法表示( )A. B. C. D.4．已知,,,则“”是“a ,b ,c 可以构成三角形的三条边”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件,则的最小值为( )A.9B.6C.4D.36．已知集合,,,若C 恰有1个真子集,则实数( )A.2 B.6 C.-2或6 D.2或67．某花卉店售卖一种多肉植物,若每株多肉植物的售价为30元,则每天可卖出25株;若每株多肉植物的售价每降低1元,则日销售量增加5株.为了使这种多肉植物每天的总销售额不低于1250元,则每株这种多肉植物的最低售价为( )A.25元B.20元C.15元D.10元8．学校统计某班45名学生参加音乐、科学、体育3个兴趣小组的情况，其中有20名学生参加了音乐小组，有21名学生参加了科学小组，有22名学生参加了体育小组，有24名学生只参加了1个兴趣小组，有12名学生只参加了2个兴趣小组，则3个兴趣小组都没参加的学生有( )A ．5名B ．4名C ．3名D ．2名Q 1-∈N ⊆Z N ⊆Q R:q a ∀<31A x x ⎧⎫=∈∈⎨⎬-⎩⎭Z Z A ={}2,0,1,2,4-{}2,0,2,4-{}0,2,4{}2,40a >0b >0c >a b c +>21b+=2a b +(){}2,1A x y y xax ==++(){},23B x y y x ==-C A B = a =二、多项选择题9．下列各组对象能构成集合的有( )A.南昌大学2024级大一新生B.我国第一位获得奥运会金牌的运动员C.体型庞大的海洋生物D.唐宋八大家10．已知A. B. C. D.11．已知二次函数（a ,b ,c 为常数,且）的部分图象如图所示,则( )A.B.C.D.不等式的解集为三、填空题12．已知13．已知,,集合,则________.14．已知四、解答题15．已知全集,集合,.（1）若,求,;（2）若,求a 的取值范围.16．给出下列两个结论：①关于x 的方程无实数根;②存在,使.a b >>>2c =-1c =-1c =2c =2y ax bx c =++0a ≠0a b +>0abc >1320a b c ++>20bx ax c -->{}21x x -<<a ==a ∈R b ∈R {}{}2,,2,2,0a b a a +=()3a b -=m n <<U =R {}23A x x =-<<{}12B x a x a =-<<2a =A B U BðB A ⊆230x mx m +-+=02x ≤≤()130m x +-=(1)若结论①正确,求m 的取值范围;(2)若结论①,②中恰有一个正确,求m 的取值范围.17．已知正数a ,b ,c 满足.(1)若(2)求18．已知,函数.（1）当时,函数的图象与x 轴交于,两点,求;（2）求关于x 的不等式的解集.19．设A 是由若干个正整数组成的集合,且存在3个不同的元素a ,b ,,使得,则称A 为“等差集”.（1）若集合,,且B 是“等差集”,用列举法表示所有满足条件的B ;（2）若集合是“等差集”,求m 的值;（3）已知正整数,证明:不是“等差集”.1abc =c =+2222a b c ++a ∈R ()23223y ax a x a =++++1a =()23223y ax a x a =++++()1,0A x ()2,0B x 3312x x +1y ≥c A ∈a b b c -=-{}1,3,5,9A =B A ⊆{}21,,1A m m =-3n ≥{}23,,,,n x x x x ⋅⋅⋅参考答案1．答案：D对B ：不是自然数,故B 错误;对C ：整数不都是自然数,如是整数但不是自然数,故C 错误;对D ：有理数都是实数,故D 正确.故选：D.2．答案：D解析：对于命题q ,是全称量词命题,当,,所以q 为全称量词命题且为假命题.故选：D.3．答案：B解析：由题意可得可为、,即x 可为0,2,-2,4,即.故选：B.4．答案：B解析：当,,,得,a ,b ,c 不能构成三角形的三边长,若a ,b ,c 是某三角形的三边长,则有,所以“”是“a ,b ,c 可以构成三角形的三条边”的必要不充分条件.故选：B.5．答案：A,则,,,所以当时,取得最小值9.故选:A1-1-3a =-2b =a <1x -1±3±{}2,0,2,4A =-5a =1b =2c =a b c +>a b c +>a b c +>21b+=12(2)1452922a b a b a b b b a a ⎛⎫+=++=+++≥+= ⎪⎝⎭=3=3b =3,3a b ==2a b +6．答案：C解析：由C 恰有1个真子集,故C 中只有一个元素,即与有且只有一个交点,将代入,有,即,解得或.故选：C.7．答案：D解析：设售价为x 元,则销售量为,销售额,整理可得,解得,所以最低售价为10元,故选：D.8．答案：B解析：设三个小组都参加的人数为x ，只参加音乐科学的人数为，只参加音乐体育的人数为，只参加体育科学的人数为，作出韦恩图，如图，由题意，，即，因为有12名学生只参加了2个兴趣小组，所以，代入解得，即三个兴趣小组都参加的有5人，所以参加兴趣小组的一共有人，21y x ax =++23y x =-23y x =-21y x ax =++()2240x a x +-+=()22160a ∆=--=6a =2a =-()255301755x x +-=-()17551250x x -≥2352500x x -+≤1025x ≤≤1y 2y 3y 12132324202122y x y y x y y x y +++++++++=++()12323632439y y y x +++=-=12312y y y ++=5x =2412541++=所以不参加所有兴趣小组的有人.故选：B9．答案：ABD解析：对于A ，因为南昌大学2024级大一新生是确定的，所以能构成集合，所以A 正确，对于B ，因为我国第一位获得奥运会金牌的运动员是确定的，所以能构成集合，所以B 正确，对于C ，因为体型庞大的海洋生物没有明确的标准，没有确定性，所以不能构成集合，所以C 错误，对于D ，因为唐宋八大家是确定的，所以能构成集合，所以D 正确.故选：ABD10．答案：AB由,故,即,即,故A 、B 正确;C 、D 错误.故选：AB.11．答案：BCD解析：由图象可知,该二次函数开口向上,故,与轴的交点为、,故,即、,对A ：,故A 错误;对B ：,故B 正确;对C ：,故C 正确;对D ：可化为,即,即,其解集为,故D 正确.故选：BCD.12．答案：解析：45414-=>1c a +>>0a b >>bc ac >()0a b c -<0c <0a >x ()1,0-()2,0()()22122y ax bx c a x x ax ax a =++=+-=--b a =-2c a =-()0a b a a +=+-=()()3220abc a a a a =⋅-⋅-=>13213480a b c a a a a ++=--=>20bx ax c -->220ax ax a --+>220x x +-<()()120x x -+<{}21x x -<<<a ===,所以.故答案为：.13．答案：8解析：由题设,若,则不满足元素的互异性,所以,显然满足题设,所以.故答案为:814．答案：解析：令,,则,.故答案为:.15．答案：（1）,b===>0>+><<a b<<a={}2,2,0a211a baa aba+=⎧=⎧⎪=⇒⎨⎨=-⎩⎪≠⎩()3328a b-==1-m n x+=<0m n y-=<m==8242242x ym x y x ym n x xxyyy⋅⋅-+=-=--+-4441331y x y xx y x y⎛⎫=---=-+≤-=-⎪⎝⎭=11-{}24A B x x=-<<{}14UB x x x=≤≥或ð（2）解析：（1）当时,,则,因为,所以;（2）当时,成立,此时,解得,当时,由,得,解得综上,16．答案：(1)(2).解析：(1)若关于x 的方程无实数根,则有,即,解得;(2)若存在,使,由时,,故时有解,即有由(1)知,若结论①正确,则,故结论①,②中恰有一个正确时,.17．答案：(1)(2)8解析：(1)若,则,(2)32a ≤2a ={}14B x x =<<{}14U B x x x =≤≥或ð{}23A x x =-<<{}24A B x x =-<< B =∅B A ⊆12a a -≥1a ≤-B ≠∅B A ⊆121223a a a a -<⎧⎪-≥-⎨⎪≤⎩1a -<≤a ≤62m -<<6m -<<2≥230x mx m +-+=()2430m m ∆=--+<()()2412260m m m m +-=-+<62m -<<02x ≤≤()130m x +-=0x =()1330m x +-=-≠1m +=2x <≤1m +≥≥62m -<<6m -<<2≥1c =ab =3b +≥=====2222222882a b c a c b c ac bc ac bc +++=++++++,当且仅当、、时,即时,等号成立,故18．答案：（1）（2）见解析解析：（1）当时,.由题可知,是方程的两个实数根,则,.由,得,则.（2）由,得.当时,不等式整理为,解得,即原不等式的解集为.当时,令,得或当时,;当时,,则原不等式的解集为;当时,;当时,.19．答案：（1）答案见解析（2）（3）证明见解析8822ab bc ac bc ac bc≥=++++()828ab bc ac bc =++≥=+a c =b c =()2ab bc +=1=1a b c ===2222a b c ++50-1a =255y x x =++1x 2x 2550x x ++=125x x +=-125x x =211222550550x x x x ⎧++=⎨++=⎩32111322225555x x x x x x ⎧=--⎨=--⎩()()()233221212121212555225752550x x x x x x x x x x ⎡⎤+=-+-+=-+-+=-+=-⎣⎦1y ≥()232220ax a x a ++++≥0a =220x +≥1x ≥-{}1x x ≥-0a ≠()()()232221220ax a x a x ax a ++++=+++=1x =-x =0a >1->221a x x x a ⎧+⎫≤-≥-⎨⎬⎩⎭或20a -<<221a a +-<-221a x x a ⎧+⎫-≤≤-⎨⎬⎩⎭2a =-1-=}1-2a <-1->221a x x a ⎧+⎫-≤≤-⎨⎬⎩⎭2m =解析：（1）因为集合,,存在3个不同的元素a ,b ,,使得,则或或.（2）因为集合是“等差集”,所以或或,计算可得或或又因为m 正整数,所以.（3）假设是“等差集”,则存在m ,n ,,,成立,化简可得,因为,,所以,所以与集合的互异性矛盾,所以不是“等差集”.{}1,3,5,9A =B A ⊆c B ∈a b b c -=-{}1,3,5,9B ={}1,3,5B ={}1,5,9B ={}21,,1A m m =-221m m =+-2211m m =+-()2221m m +=-m =0=2m =m =2m ={}22,,,,n x x x x ⋅⋅⋅{}1,2,3,,q n ∈ m n q <<2n m q x x x =+2m n q n x x --=+0m n x ->*x ∈N 1q n -≥21q n x x ->≥≥1x ={}22,,,,n x x x x ⋅⋅⋅{}22,,,,n x x x x ⋅⋅⋅。

全国名校高中（陕西西安）高一数学下学期第一次考试3月月考数学试题总分： 100分时间： 100分钟一、选择题（本题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．完成下列两项调查：①一项对“小彩旗春晚连转四小时”的调查中有10 000人认为这是成为优秀演员的必经之路，有9 000人认为太残酷，有1 000人认为无所谓.现要从中随机抽取200人做进一步调查.②从某中学的15名艺术特长生中选出3名调查学习负担情况，宜采用的抽样方法依次是（）A．①简单随机抽样，②系统抽样 B．①分层抽样，②简单随机抽样C．①系统抽样，②分层抽样 D．①②都用分层抽样2．根据《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20～80 mg/100 mL(不含80)之间，属于酒后驾车，处暂扣一个月以上三个月以下驾驶证，并处200元以上500元以下罚款；血液酒精浓度在80 mg/100 mL(含80)以上时，属醉酒驾车，处十五日以下拘留和暂扣三个月以上六个月以下驾驶证，并处500元以上2 000元以下罚款．据《法制晚报》报道，2009年8月15日至8月28日，全国查处酒后驾车和醉酒驾车共28 800人，如图是对这28 800人血液中酒精含量进行检测所得结果的频率分布直方图，则属于醉酒驾车的人数约为 ( )．A．2 160 B．2 880 C．4 320 D．8 6403．下列说法正确的是 ( )．A．任何事件的概率总是在(0，1)之间B．频率是客观存在的，与试验次数无关C．概率是随机的，在试验前不能确定D．随着试验次数的增加，频率一般会越来越接近概率4．将一个长与宽不等的长方形，沿对角线分成四个区域，如图所示涂上四种颜色，中间装个指针，使其可以自由转动，对指针停留的可能性下列说法正确的是 ( )． A ．蓝白区域大 B ．红黄区域大 C ．一样大 D ．由指针转动圈数决定5．从1、2、3、4、5、6这6个数字中，一次性任取两数，两数都是偶数的概率是 ( )． A.12B.13C.14D.156．如果执行下面的算法框图，输入x ＝－2，h ＝0.5，那么输出的各个数的和等于( )． A ．3 B ．3.5 C ．4 D ．4.57．已知直线y ＝x ＋b ，b ∈[－2，3]，则直线在y 轴上的截距大于1的概率为( )． A.15B.25C.35D.458. 如图是根据某校10位高一同学的身高(单位：cm)画出的茎叶图，其中左边的数字从左到右分别表示学生身高的百位数字和十位数字，右边的数字表示学生身高的个位数字，从图中可以得到这10位同学身高的中位数是 ( )． A ．161 cmB ．162 cmC ．163 cmD ．164 cm9．如图所示是一样本的频率分布直方图，则由图形中的数据，可以估计众数与中位数分别是 ( )．A ．12.5 13B ．12.5 12.5C．13 12.5D．13 1310. 甲、乙两位同学在高三的5次月考中数学成绩统计如茎叶图所示，若甲、乙两人的平均成绩分别为x甲，x乙，则下列叙述正确的是( )．A．x甲>x乙；乙比甲成绩稳定 B．x甲>x乙；甲比乙成绩稳定C．x甲<x乙；乙比甲成绩稳定 D．x甲<x乙；甲比乙成绩稳定二、填空题（本题共4小题，每小题4分，共16分)11、某鱼贩一次贩运草鱼、青鱼、鲢鱼、鲤鱼及鲫鱼分别为80条、20条、40条、40条、20条，现从中抽取一个容量为20的样本进行质量检测，若采用分层抽样的方法抽取样本，则抽取的青鱼与鲤鱼共有______条．12、如右图，面积为4的矩形ABCD中有一个阴影部分，若往矩形ABCD中随机投掷1 000个点，落在矩形ABCD的非阴影部分中的点数为400个，试估计阴影部分的面积为。

高一上学期第一次月考数学试题(附答案解析)学校:___________姓名：___________班级：___________考号：___________第I卷（选择题）一、单选题（本大题共8小题，共32.0分。

在每小题列出的选项中，选出符合题目的一项）1. 已知集合A={−1,1}，B={x|ax=1}，若A∩B=B，则a的取值集合为( )A. {1}B. {−1}C. {−1,1}D. {−1,0,1}2. 下列存在量词命题是假命题的是( )A. 存在x∈Q，使2x−x3=0B. 存在x∈R，使x2+x+1=0C. 有的素数是偶数D. 有的有理数没有倒数3. 定义集合A，B的一种运算：A⊗B={x|x=a2−b,a∈A,b∈B}，若A={−1,0}，B={1,2}，则A⊗B 中的元素个数为( )A. 1B. 2C. 3D. 44. 已知x，y，z为非零实数，代数式x|x|+y|y|+z|z|+xyz|xyz|的值所组成的集合是M，则下列判断正确的是( )A. 4∈MB. 2∈MC. 0∉MD. −4∉M5. 一批救灾物资随26辆汽车从某市以vkm/h的速度送达灾区，已知运送的路线长400km，为了安全起见，两辆汽车的间距不得小于(v20)2km，那么这批物资全部到达灾区最少需要时间( )A. 5 hB. 10 hC. 15 hD. 20 h6. 已知集合A={x|ax2−(a+1)x+1<0}，B={x|x2−3x−4<0}，且A∩B=A，则实数a的取值范围是( )A. a≤14B. 0<a≤14C. a≥14D. 14≤a<1或a>17. 如图，抛物线y=ax2+bx+c的对称轴是直线x=1，下列结论：①abc>0；②b2−4ac>0；③8a+ c<0；④5a+b+2c>0，正确的有( )A. 4个B. 3个C. 2个D. 1个8. 某单位周一、周二、周三开车上班的职工人数分别是14，10，8.若这三天中至少有一天开车上班的职工人数是20，则这三天都开车上班的职工人数的最大值是( )A. 6B. 5C. 7D. 8二、多选题（本大题共4小题，共16.0分。

北京市2024-2025学年高一上学期9月月考数学试卷班级______姓名______学号______2024.09.30（答案在最后）一、选择题（共8个小题，每题5分，共40分．每小题只有一个正确选项，请选择正确答案．．．．．．．填在答题纸相应的题号处．．．．．．．．．．．）1.已知集合{10}A xx =-≤≤∣，集合{1,0,1,2}B =-，则A B = （）A.RB.{10}x x -≤≤∣C.{1,0}- D.{1,0,1}-【答案】C【解析】【分析】根据交集运算求解即可.【详解】因为集合{10}A xx =-≤≤∣，集合{1,0,1,2}B =-，所以{}1,0A B ⋂=-.故选：C2.下列命题中，正确的是（）A.若a b >，则22ac bc > B.若,a b c d >>，则a c b d +>+C.若,a b c d >>，则ac bd> D.若a b >，则11a b >【答案】B【解析】【分析】利用不等式的性质及举反例即可判断.【详解】对A 选项，当0c =时不等式不成立,故A 选项错误；B 选项，满足不等式的同向可加性，故B 选项正确；C 选项，当2,1,1,2a b c d ===-=-，则ac bd =，故C 选项错误；D 选项，当1,2a b =-=-时，11a b<，故D 选项错误.故选：B 3.方程组2202x y x y +=⎧⎨+=⎩的解集是（）A.{(1,1),(1,1)}-- B.{(1,1),(1,1)}--C.{(2,2),(2,2)}-- D.{(2,2),(2,2)}--【答案】B【解析】【分析】根据消元法求得不等式组的解，结合集合的表示方法，即可求解.【详解】由题意，将y x =-代入222x y +=，可得21x =，即1x =±，当1x =时，1y =-；当1x =-时，1y =，所以方程组的解集为{(1,1),(1,1)}--.故选：B.4.下列不等式中，解集为{1xx <∣或3}x >的不等式是（）A .2430x x -+≥ B.2430x x -+< C.103x x -≥- D.|2|1x ->【答案】D【解析】【分析】根据一元二次不等式的解法、分式不等式的解法和绝对值不等式的解法分别解各选项不等式即可求解.【详解】由2430x x -+≥可得()()130x x --≥，解得1x ≤或3x ≥，故A 错误；由2430x x -+<可得13x <<，故B 错误；由103x x -≥-可得()()()13030x x x --≥-≠，解得1x ≤或3x >，故C 错误；由|2|1x ->可得21x ->或21x -<-，即1x <或3x >，故D 正确.故选：D5.“0a b >>”是“22a b >”的（）A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】A【解析】【分析】根据充分不必要条件的概念判断即可.【详解】当0a b >>时，22a b >；当22a b >时，a b >，不一定0a b >>，所以“0a b >>”是“22a b >”的充分不必要条件.故选：A.6.平流层是指地球表面以上10km (不含)到50km (不含)的区域,下述不等式中,x 能表示平流层高度的是A.|10|50x +< B.|10|50x -< C.|30|20x +< D.|30|20x -<【答案】D【解析】【分析】根据绝对值的几何意义即可得解|30|20x -<.【详解】解析:如图：设(10),(50)A B ,则AB 的中点为(30)M ,由距离公式可得|30|20x -<.答案:D【点睛】此题考查根据绝对值的几何意义解决实际问题，关键在于正确理解绝对值的几何意义.7.若不等式04x <<是||x a <成立的充分条件，则a 的取值范围是（）A.1a ≥ B.4a ≥ C.1a ≤ D.4a ≤【答案】B【解析】【分析】由题意知()()0,41,1a a ⊆-+可得1014a a -≤⎧⎨+≥⎩，解不等式即可得出答案.【详解】由题设，不等式a x a -<<且>0成立的充分条件是04x <<，则()()0,4,a a ⊆-，所以4a ≥，所以实数a 的取值范围是4a ≥.故选：B.8.已知集合{}{}2221,N ,21,N P yy x x x Q y y x x x ==+-∈==-+-∈∣∣，则P Q = （）A.{}1- B.{0} C.∅ D.N 【答案】A【解析】【分析】由两个方程相等可求得两曲线交点的横坐标，根据集合的几何意义求出纵坐标的值即为交集的结果.【详解】由222121x x x x +-=-+-，解得0x =，当0x =时，2221211x x x x +-=-+-=-，所以1{}P Q ⋂=-.故选：A二、填空题（共6个小题，每题5分，共30分．请将正确答案填在答题卡相应的题号处．．．．．．．．．．．．．．．．．）．9.命题2R,230x x x ∀∈-+>的否定是______．【答案】R x ∃∈，2230x x -+≤【解析】【分析】根据全称量词命题的否定求解.【详解】命题2R,230x x x ∀∈-+>的否定是R x ∃∈，2230x x -+≤.故答案为：R x ∃∈，2230x x -+≤10.已知全集U ＝{1，2，3，4，5，6}，集合P ＝{1，3，5}，Q ＝{1，2，4}，则（U P ð）∪Q ＝____．【答案】{1，2，4，6}，【解析】【分析】由已知，先求出U P ð，再求（U P ð）∪Q ．【详解】∵U ＝{1，2，3，4，5，6}，集合P ＝{1，3，5}，Q ＝{1，2，4}，∴U P ð＝{2，4，6}，∴（U P ð）∪Q ＝{1，2，4，6}，故答案为：{1，2，4，6}，11.已知集合{1,2,3}A ⊆，集合A 可以为______（写出符合要求的所有A ）【答案】{}{}{}{}{}{}{},1,2,3,1,2,1,3,2,3,1,2,3∅【解析】【分析】写出集合的子集即可得解.【详解】因为集合{1,2,3}A ⊆，所以集合A 可以为{}{}{}{}{}{}{},1,2,3,1,2,1,3,2,3,1,2,3∅.故答案为：{}{}{}{}{}{}{},1,2,3,1,2,1,3,2,3,1,2,3∅12.已知12,x x 是关于x的一元二次方程210x -+=的两根，则12x x +=______；1211x x +=______．【答案】①.②.【解析】【分析】根据一元二次方程根与系数的关系求解.【详解】由一元二次方程根与系数的关系可知，12x x +=，121x x ⋅=，所以12121211x x x x x x ++==⋅.故答案为：；13.若2{{1,2,4,}a ⊆，则a =________________________【答案】4，16，0【解析】【分析】依题意有{}21,2,4,a，逐个列方程求解，并检验元素的互异性.【详解】依题意有{}21,2,4,a1≠，2=时，216a =，满足题意，则4a =；4=时，2256a =，满足题意，则16a =；2a =时，0a =或1a =，0a =时满足题意，1a =时与元素的互异性矛盾.综上，4a =或16a =或0a =时满足题意，故答案为：4，16，014.若对2R,230x ax ax ∀∈-+>恒成立是真命题，则实数a 的取值范围是______【答案】[)0,3【解析】【分析】分0,0a a =≠讨论，根据一元二次不等式恒成立求解.【详解】当0a =时，原不等式为30>，对任意实数都成立，满足题意；当0a ≠时，2R,230x ax ax ∀∈-+>恒成立，需满足()202120a a a >⎧⎪⎨--<⎪⎩，即003a a >⎧⎨<<⎩，解得0<<3a .综上，实数a 的取值范围是[)0,3.故答案为：[)0,3三、解答题（共3个小题，每题10分，其30分，请将解题过程和答案写在规定的区域内．．．．．．．．．．．．．．．．．．．）15.已知a ，b 为正数，且a b ≠，比较33+a b 与22a b ab +的大小．【答案】3322a b a b ab +>+【解析】【分析】通过作差，提取公因式便可得出33222()()()a b a b ab a b a b +-+=-+，并根据条件可以判断2()()0a b a b -+>，这样即可得出所比较两个式子的大小关系【详解】33223322()()a b a b ab a b a b ab +-+=+-- 22()()a ab b a b =---22()()a b a b =--2()()a b a b =-+；0a > ，0b >且a b ≠；2()0a b ∴->，0a b +>；2()()0a b a b ∴-+>；即3322()()0a b a b ab +-+>；3322a b a b ab ∴+>+．【点睛】本题主要考查作差法比较两个代数式的大小关系，分解因式法的运用，以及平方差公式，属于基础题．16.一元二次方程210ax bx ++=的解集是12,23⎧⎫-⎨⎬⎩⎭，求实数a ，b 的值，并求方程230bx ax b +--=的解集．【答案】13,2a b =-=,{}1,7-【解析】【分析】根据一元二次方程根与系数的关系求,a b ，再解一元二次方程得解.【详解】因为一元二次方程210ax bx ++=的解集是12,23⎧⎫-⎨⎬⎩⎭，所以122312123b a a⎧-+=-⎪⎪⎨⎪-⋅=⎪⎩，解得13,2a b =-=，所以方程230bx ax b +--=为2670x x --=，解得7x =或1x =-，所以方程的解集为{}1,7-.17.已知集合{}22,(,1)A x a x a B ∞=<<-=-∣．（1）若A B ⊆，求实数a 的取值范围；（2）若U B A ⊆ð，求实数a 的取值范围．【答案】（1）2⎡⎤⎣⎦（2）[)1,-+∞【解析】【分析】（1）分类讨论，根据子集列出不等式求解；（2）分集合是否为空集讨论，根据子集关系列不等式得解.【小问1详解】当22a a -≤时，即12a -≤≤时，A =∅，满足A B ⊆；当A ≠∅时，若A B ⊆，则需22221a a a ⎧<-⎨-≤⎩，解得1a ≤<-，综上，实数a的取值范围2⎡⎤⎣⎦.【小问2详解】由（1）知，当12a -≤≤时，A =∅，所以R U A =ð，满足U B A ⊆ð；当1a <-或2a >时，(])2,2,U A a a ⎡=-∞-+∞⎣ ð，由U B A ⊆ð可得1a ≤，又2a >，所以2a >.综上，实数a 的取值范围[)1,-+∞.。

2022-2023学年全国高一上数学月考试卷考试总分：110 分 考试时间： 120 分钟学校：__________ 班级：__________ 姓名：__________ 考号：__________注意事项：1．答题前填写好自己的姓名、班级、考号等信息; 2．请将答案正确填写在答题卡上;卷I （选择题）一、 选择题 （本题共计 8 小题 ，每题 5 分 ，共计40分 ）1. 已知全集，，，则( )A.B.C.D.2. 命题“，”的否定是( )A.，B.，C.，D.，3. 若，则“”是“”的( )A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分又不必要条件4. 若函数的定义域为，则实数的取值范围是 A.B.U =R A ={x |−2x <0}x 2B ={x |x ≥1}A ∪(B)=∁U (0,+∞)(−∞,1)(−∞,2)(0,1)∀x ≥0−2x ≥1e x ∀x ≥0−2x <1e x ∀x <0−2x <1e x ∃x ≥0−2x <1e x ∃x <0−2x <1e x a ∈R a >2|a|>2y =mx −1m +4mx +3x 2R m ()(0,]34(0,)340,]3C.D.5. 已知，，，则，，的大小关系是（ ）A.B.C.D.6. 不等式的解集为( )A.B.C. D.7. 已知，则( )A.B.C.D.8. 已知函数的定义域为，且是偶函数，若，在上单调递增，则不等式的解集为( )A.B.C.D.二、 多选题 （本题共计 4 小题 ，每题 5 分 ，共计20分 ）[0,]34[0,)34a =3+log 2log 23–√b =9−log 2log 23–√c =2log 3a b c a =b <ca =b >ca <b <ca >b >c5−>4x x 2(−∞,−5)∪(1,+∞)(−∞,−1)∪(5,+∞)(−1,5)(−5,1)f (x +1)=x +2f (0)=12−1f (x)R f (x +1)f (2)=3f (x)(−∞,1]f (2x −1)>3(−∞,)∪(,+∞)1232(,)1232(−∞,1)∪(3,+∞)(1,3)(x)={，−2≤x <1，29. 已知函数关于函数的结论正确的是( )A.的定义域为B.的值域为C.若，则的值是D.的解集为10. 已知，若关于的不等式的解集中的整数恰有个，则可能为( )A.B.C.D.11. 已知，则 A.为奇函数B.为偶函数C.在上单调递增D.在上单调递减12. 已知，且，则下列说法中正确的有（）A.的最大值为B.的最大值为C.的最小值为D.的最小值为卷II （非选择题）三、 填空题 （本题共计 4 小题 ，每题 5 分 ，共计20分 ）f (x)={，−2≤x <1，x 2−x +2，x ≥1，f (x)f (x)Rf (x)(−∞,4]f (x)=2x −2–√f (x)<1(−1,1)a +2>b >0x (+2a)+2bx −≤0a 2x 2b 24a 012231f (x)=1−2x1+2x ()f (x)f (x)f (x)R f (x)R x >0,y >02x +y =2xy 124+x 2y 22+4x 2y 4+2x xy 4π13. 若点在函数的图象上，则的值为________． 14. 函数的定义域为________．15. 已知函数 若存在实数 ，当时，满足，则的取值范围是________．16. 已知函数 有以下结论：①任意 ，等式 恒成立；②任意 ，方程 有两个不等实数根；③存在无数个实数，使得函数 在上有个零点；④函数 在区间 上单调递增.其中正确结论有________.四、 解答题 （本题共计 6 小题 ，每题 5 分 ，共计30分 ）17. 已知函数＝．（1）当＝时，求函数在的值域；（2）若存在零点，求的取值范围． 18. 已知集合＝，＝．（1）若＝，求的取值范围；（2）若，求的取值范围．19. 已知函数，且满足，.求函数的解析式；判断函数在区间上的单调性，并用定义证明其结论.20. 已知正实数，，，满足.证明：；证明：. 21.已知实数满足关系式（且，且)．若，求的表达式；在的条件下，若当时，有最小值，求和的值．(a,27)y =x 3tan πaf (x)=(2x −1)log 2f(x)={|x|，0<x <4,log 4sin(x −)，4≤x ≤12,π4π2,,,x 1x 2x 3x 4<<<x 1x 2x 3x 4f()=f()=f()=f()x 1x 2x 3x 4⋅⋅⋅−50⋅x 1x 2x 3x 4x 1x 2f (x)=,x ∈(−1,1)x |x|−1x ∈(−1,1)f (−x)+f (x)=0m ∈[0,+∞)|f (x)|=m k g(x)=f (x)−kx (−1,1)3f (x)(−1,1)f(x)2a ⋅−−14x 2x a 1f(x)x ∈[−3,0]f(x)a A {x |0≤x ≤2}B {x |a ≤x ≤3−2a}(A)∪B ∁U R a A ∩B ≠B a f(x)=2x +ax +b f(2)=13f(9)=32(1)f(x)(2)f(x)[0,+∞)a b c ab +bc +ac =abc (1)a +b +c ≥9(2)++≥1b a 2c b 2a c 2t =log a t a 3log t y a3a >0a ≠1t >0t ≠1(1)t =a x y =f(x)(2)(1)x ∈(0,2]y 8a x22. 22已知二次函数f(x)=ax2+bx,(a,b为常数,且a≠0)满足条件f(2-x)=f(x-D),且方程f(x)=x有两个相等的安根(1)求f(x)的解析式(2)设g(x)=kx+1,若F(x)=g(x)-f(x),求F(x)在[,2上的最小值3)是存在实数m,川(m 11参考答案与试题解析2022-2023学年全国高一上数学月考试卷一、 选择题 （本题共计 8 小题 ，每题 5 分 ，共计40分 ）1.【答案】C【考点】交、并、补集的混合运算【解析】本题主要考查了交、并、补集的混合运算的相关知识点，需要掌握求集合的并、交、补是集合间的基本运算，运算结果仍然还是集合，区分交集与并集的关键是“且”与“或”，在处理有关交集与并集的问题时，常常从这两个字眼出发去揭示、挖掘题设条件，结合图或数轴进而用集合语言表达，增强数形结合的思想方法才能正确解答此题．【解答】解：由题意得，.∵全集，，∴，则.故选．2.【答案】C【考点】命题的否定【解析】全称命题的否定为特称命题即可得出答案.【解答】解：由全称命题的否定为特称命题可知，命题“，”的否定是“，”.故选.3.Venn A =(0,2)U =R B ={x |x ≥1}B =(−∞,1)∁U A ∪(B)=(−∞,2)∁U C ∀x ≥0−2x ≥1e x ∃x ≥0−2x <1e x C【答案】A【考点】必要条件、充分条件与充要条件的判断【解析】（1）根据题目所给信息进行解题即可.【解答】解：已知 ，解得或，则“”是“”的充分不必要条件.故选.4.【答案】D【考点】函数的定义域及其求法【解析】由函数的定义域为，则对于任意，有恒不等于成立，然后分和讨论求解．当时需要分母所对应方程的判别式小于．【解答】解：∵的定义域为，当，∴满足题意；当时，由，解得．综上，当，即时，函数的定义域为．故选．5.【答案】B【考点】|a|>2a <−2a >2a >2|a|>2A y =mx −1m +4mx +3x 2R x ∈R m +4mx +3x 20m =0m ≠0m ≠00y =mx −1m +4mx +3x 2R m =0m +4mx +3=3x 2m ≠0Δ=16−12m <0m 20<m <340≤m <34m ∈[0,)34y =mx −1m +4mx +3x 2R D不等式比较两数大小【解析】利用对数的运算性质可求得，，而，从而可得答案．【解答】解：∵，，∴，又，∴．故选：．6.【答案】D【考点】一元二次不等式的解法【解析】不等式化为，求出解集即可．【解答】解：不等式可化为，即解得，所以不等式的解集为.故选．7.【答案】A【考点】函数解析式的求解及常用方法函数的求值【解析】用换元法，设，得，从而得，即，即可求出结果.【解答】a =3log 23–√b =3>1log 23–√0<c =2<1log 3a =3+=3log 2log 23–√log 23–√b =9−==3>1log 2log 23–√log 293–√log 23–√a =b >10<c =2<1log 3a =b >c B +4x −5<0x 25−>4x x 2+4x −5<0x 2(x +5)(x −1)<0−5<x <1(−5,1)D x +1=t x f (t)f (x)解：设，则.由，得，即，则．故选．8.【答案】B【考点】奇偶性与单调性的综合函数奇偶性的性质函数单调性的性质【解析】答案未提供解析．【解答】解：因为是偶函数，所以函数的图象关于对称，则，因为在上单调递增，所以等价于，即．故选．二、 多选题 （本题共计 4 小题 ，每题 5 分 ，共计20分 ）9.【答案】B,C【考点】分段函数的应用函数的值域及其求法函数的定义域及其求法【解析】利用分段函数的定义域、值域、自变量等知识对四个选项逐一进行判断正误即可.【解答】x +1=t x =t −1f (x +1)=x +2f (t)=(t −1)+2=t +1f (x)=x +1f(0)=0+1=1A f (x +1)f (x)x =1f (0)=f (2)=3f (x)(−∞,1]f (2x −1)>30<2x −1<2<x <1232B A f (x)[−2,1)∪[1,+∞)[−2,+∞)A解：，的定义域为，即，故错误；，当时，，当时，，则的值域为，即，故正确；，当时，，此时或(舍去)，当时，，(舍去)，故的值为，故正确；，当时，，此时，即，当时，，此时，即，综上可得的解集为，故错误.故选.10.【答案】B,C【考点】一元二次不等式的应用一元二次不等式的解法【解析】此题暂无解析【解答】解：，由于该不等式的解集中的整数恰有个，则有，，故．由不等式，解得.要使该不等式的解集中的整数恰有个，且，那么，得.又，所以，则.故选．11.【答案】A,D【考点】奇偶性与单调性的综合【解析】可先得出的定义域为，求，从而得出为奇函数，根据指数函数的单调性便可看出增大时，减小，从而得到在上单调递减，这样便可找出正确选项．A f (x)[−2,1)∪[1,+∞)[−2,+∞)A B −2≤x <10≤f (x)≤4x ≥1f (x)≤1f (x)[0,4]∪(−∞,1](−∞,4]B C −2≤x <1f (x)==2x 2x =−2–√2–√x ≥1f (x)=−x +2=2x =0x −2–√C D −2≤x <1f (x)=<1x 2−1<x <1−1<x <1x ≥1f (x)=−x +2<1x >1x >1f (x)<1(−1,1)∪(1,+∞)D BC (+2a)+2bx −≤0a 2x 2b 24+2a >0a 2a +2>0a>0(+2a)a 2+2bx −≤0x 2b 2−≤x ≤b a b a +240<<1b a +2−4<≤−3−b a 3a ≤b <4a a +2>b a +2>3a 0<a <1BC f (x)R f (−x)=−f (x)f (x)x f (x)f (x)R【解答】解：，，的定义域是，定义域关于原点对称，，是奇函数，故正确，错误；，设，且，则，，，，，，，即，，在上为减函数，故错误，正确．故选．12.【答案】A,C,D【考点】基本不等式基本不等式在最值问题中的应用【解析】根据均值不等式逐项分析解答【解答】解：，，， 由均值不等式 ，，，当且仅当，即，时，“”成立， ，故正确；，，当且仅当，即，时，“”成立，，故错误；，由均值不等式，，∵>02x 1+>12x ∴f (x)=1−2x1+2xR f (−x)===−f (x)1−2−x 1+2−x −12x +12x ∴f (x)A B f (x)==−1+1−2x 1+2x 21+2x ∀,∈(−∞,+∞)x 1x 2<x 1x 2f ()−f ()=−1++1−x 1x 221+2x 121+2x 2=2(−)2x 22x 1(1+)(1+)2x 12x 2∵<x 1x 2∴0<<2x 12x 2∴−>02x 22x 11+>02x 11+>02x 2∴>02(−)2x 22x 1(1+)(1+)2x 12x 2f ()−f ()>0x 1x 2∴f ()>f ()x 1x 2∴f (x)R C D AD ∵x >0y >02x +y =2≤≤ab −−√a +b 2+a 2b 22−−−−−−√A ∵=1≥2x +y 22xy −−−√2x =y x =12y =1=∴xy ≤12A B ∵=1≤2x +y 24+x 2y 22−−−−−−−−√2x =y x =12y =1=∴4+≥2x 2y 2B C +=+≥2=2=44x 2y 22x 2y 22x+y −−−−√22−−√=1当且仅当，当且仅当，即，时，“”成立，，故正确；，，，由均值不等式，， 当且仅当，即时“”成立，故正确．故选．三、 填空题 （本题共计 4 小题 ，每题 5 分 ，共计20分 ）13.【答案】【考点】幂函数的概念、解析式、定义域、值域【解析】把点代入，求出的值，再计算的值．【解答】解：把点代入得，，解得，所以．故答案为：．14.【答案】【考点】函数的定义域及其求法【解析】根据函数的解析式，列出使解析式有意义的不等式组，求出解集即可．=4x 2y 2x =y x =12y =1=∴+≥44x 2y C D ∵2x +y =2∴x +=1y 2(+)(x +)=2+++2x x y y 2y x x 2y x 2=2++y x x (2x +y)2y ≥2+2⋅y x x (2x +y)2y −−−−−−−−−−−−√=2+2=42x +y 2−−−−−−√=y x x (2x +y)2y x =y =23=D ACD 3–√(a,27)y =x 3a tanπa (a,27)y =x 3=27a 3a =3tan ==πaπ33–√3–√(，+∞)12f(x)【解答】解：函数，，解得；∴的定义域为．故答案为：.15.【答案】【考点】分段函数的应用函数单调性的性质【解析】此题暂无解析【解答】解：由题意得，函数画出函数的图象，如图所示，令，则 .由图象可知，设 和函数 的图象有四个交点，可得 ，其中 ，则 ，解得 ，且，则,所以 ，其中 .设，则当时，函数单调递增，则，所以的取值范围是 .故答案为：.f(x)=(2x −1)log 22x −1>0x >12f(x)(，+∞)12(,+∞)12(−2，10)f(x)={|x|,0<x <4，log 4sin(x −),4≤x ≤12π4π2={|x|,0<x <4,log 4−cos(x),4≤x ≤12,π4y =a 0<a <1y =a y =f(x)0<<<4<<8<<12x 1x 2x 3x 4=−log 4x 1log 4x 2+==0log 4x 1log 4x 2log 4x 1x 2=1x 1x 2+=16x 3x 4=16−x 4x 3⋅⋅⋅−50⋅x 1x 2x 3x 4x 1x 2=1×(16−)−50×1x 3x 3=−+16−50=−(−8+14x 23x 3x 3)24<<6x 3g(x)=−(x −8+14)2x ∈(4,6)g(x)g(4)=−2,g(6)=10⋅⋅⋅−50⋅x 1x 2x 3x 4x 1x 2(−2,10)(−2，10)16.【答案】①③【考点】函数恒成立问题根的存在性及根的个数判断奇偶性与单调性的综合【解析】此题暂无解析【解答】解：①，即函数为奇函数，∴ 恒成立，∴①正确；由①知 为奇函数，∴ 为偶函数，当时，即时，方程 只有一个实根，∴②错误；③由得，，∴，即是函数的一个零点，又函数 为奇函数，且在上单调递减，∴可以存在无数个实数，使得函数在上有个零点，∴③正确；④当 时，为减函数，当时，f (x)=,x ∈(−1,1)x |x|−1f (−x)==−=−f (x),x ∈(−1,1)−x |x|−1x |x|−1f (x)f (−x)+f (x)=0f (x)=,x ∈(−1,1)x |x −1|f (x)|x =0|f (0)|=0m =0|f (x)|=m g(x)=f (x)−kx =0f (x)=kx f (0)=0x =0f (x)(−1,1)k g(x)=f(x)−kx(−1,1)3x ∈[0,1)f (x)=x |x|−1=x x −1=x −1+1x −1≤0x ∈(−1,0]f (x)=x |x|−1=x −x −1=x +1−1−x −1−1+1为减函数，综上函数在上为单调函数，且单调递减，④错误.故答案为：①③.四、 解答题 （本题共计 6 小题 ，每题 5 分 ，共计30分 ）17.【答案】当＝时，＝＝，令＝，，可得那么＝＝根据二次函数的图象，可得值域为．由存在零点，即＝有解转化为＝在有解①当＝时，可得＝，不成立；②当时，对称轴图象过，显然不成立；③当时，对称轴，图象过，必有一个正根，显然存在零点，成立；综上，的取值范围是【考点】函数的值域及其求法【解析】（1）当＝时，＝＝，转化为二次函数问题即可求解的值域；（2）转化为二次函数存在零点，求的取值范围即可．【解答】当＝时，＝＝，令＝，，可得那么＝＝根据二次函数的图象，可得值域为．由存在零点，即＝有解转化为＝在有解①当＝时，可得＝，不成立；②当时，对称轴图象过，显然不成立；③当时，对称轴，图象过，必有一个正根，显然存在零点，成立；综上，的取值范围是=−1+1x +1≥0f (x)(−1,1)a 1f(x)2⋅−−14x 2x 2(−−12x )22x t 2x x ∈[−3,0]t ∈[,1]18g(t)2−t −1t 22(t −−14)298[−,0]98f(x)2a(−−12x )22x 02a −m −1m 20(0,+∞)a 0m −1<0a <0m =<014a (0,−1)a >0m =>014a (0,−1)a (0,+∞)a 1f(x)2⋅−−14x 2x 2(−−12x )22x x ∈[−3,0]a a 1f(x)2⋅−−14x 2x 2(−−12x )22x t 2x x ∈[−3,0]t ∈[,1]18g(t)2−t −1t 22(t −−14)298[−,0]98f(x)2a(−−12x )22x 02a −m −1m 20(0,+∞)a 0m −1<0a <0m =<014a (0,−1)a >0m =>014a (0,−1)a (0,+∞)18.【答案】由集合＝，所以＝，又＝，＝，所以，解得；所以实数的取值范围是．若＝，则，当＝时，；当时，有，要使，则，解得；综上知，实数的取值范围是；所以时的取值范围是的补集，为．【考点】交、并、补集的混合运算交集及其运算【解析】此题暂无解析【解答】此题暂无解答19.【答案】解：∵，，∴代入可得方程组解得∴函数的解析式为.在区间上是增函数．证明如下：任取，且，A {x |0≤x ≤2}A ∁U {x |x <5或x >2}B {x |a ≤x ≤3−4a}(A)∪B ∁U R a ≤0a (−∞,0]A ∩B B B ⊆A B ∅6−2a <a B ≠∅a ≤1B ⊆A a A ∩B ≠B a (1)f(2)=13f(9)=32 =,2×2+a 2+b13=,2×9+a 9+b 32{a =−3,b =1,f(x)f(x)=2x −3x +1(2)f(x)[0,+∞)，∈[0,+∞)x 1x 2<x 1x 2()−f()=−则.因为，所以，，所以，即，所以函数在区间上是增函数．【考点】函数解析式的求解及常用方法函数单调性的判断与证明【解析】此题暂无解析【解答】解：∵，，∴代入可得方程组解得∴函数的解析式为.在区间上是增函数．证明如下：任取，且， 则.因为，所以，，所以，即，所以函数在区间上是增函数．20.【答案】证明：因为，所以，所以，f()−f()=x 1x 2−x 1x 2(+1)(+1)x 1x 20<<x 1x 2−<0x 1x 2(+1)(+1)>0x 1x 2f()−f()=<0x 1x 2−x 1x 2(+1)(+1)x 1x 2f()<f()x 1x 2f(x)[0,+∞)(1)f(2)=13f(9)=32 =,2×2+a 2+b 13=,2×9+a 9+b 32{a =−3,b =1,f(x)f(x)=2x −3x +1(2)f(x)[0,+∞)，∈[0,+∞)x 1x 2<x 1x 2f()−f()=x 1x 2−x 1x 2(+1)(+1)x 1x 20<<x 1x 2−<0x 1x 2(+1)(+1)>0x 1x 2f()−f()=<0x 1x 2−x 1x 2(+1)(+1)x 1x 2f()<f()x 1x 2f(x)[0,+∞)(1)ab +bc +ac =abc ++=11a 1b 1c a +b +c =(a +b +c)⋅(++)1a 1b 1c =3++++++a b b a a c c a c b b c ≥3+2+2+2=9⋅a b b a −−−−−√⋅a c c a −−−−−√⋅c b b c−−−−−√a =b =c当且仅当时，等号成立，所以．，当且仅当时，等号成立，所以．【考点】基本不等式在最值问题中的应用【解析】此题暂无解析【解答】证明：因为，所以，所以，当且仅当时，等号成立，所以．，当且仅当时，等号成立，所以．21.【答案】解：由，得，由，，知，代入上式得，a =b =c a +b +c ≥9(2)++b a 2c b 2ac 2=+++++−1b a 2c b 2a c 21a 1b 1c =(+)+(+)+(+)−1b a 21bc b 21c a c 21a≥++−1=12a 2b2ca =b =c ++≥1b a 2c b 2a c 2(1)ab +bc +ac =abc ++=11a 1b 1c a +b +c =(a +b +c)⋅(++)1a 1b 1c =3++++++a b b a a c c a c b b c ≥3+2+2+2=9⋅a b b a −−−−−√⋅a c c a −−−−−√⋅c b b c −−−−−√a =b =c a +b +c ≥9(2)++b a 2c b 2a c 2=+++++−1b a 2c b 2a c 21a 1b 1c =(+)+(+)+(+)−1b a 21bc b 21c a c 21a ≥++−1=12a 2b 2ca =b =c ++≥1b a 2cb 2ac 2(1)=log a ta 3log t ya 3t −3=y −3a log a log t log t t =a x t ≠1x =t ≠0log a x −3=−+y 3x 1x log a y =(x ≠0)−3x+32∴，即．令，则，①若，要使在区间上有最小值， 则在上应有最大值，但在上不存在最大值，不符合题意．②若，要使在区间上有最小值，则在上应有最小值．∴当时，，，由，得．综上，可知所求，．【考点】函数单调性的性质函数解析式的求解及常用方法【解析】此题暂无解析【解答】解：由，得，由，，知，代入上式得，∴，即．令，则，①若，要使在区间上有最小值， 则在上应有最大值，但在上不存在最大值，不符合题意．②若，要使在区间上有最小值，则在上应有最小值．∴当时，，，由，得．y =−3x +3log a x 2y =(x ≠0)a −3x+3x 2(2)u =−3x +3=+(x≠0)x 2(x −)32234y =(u≠3)a u 0<a <1y =a −3x+3x 2(0,2]8u =+(x −)32234(0,2]u (0,2]a >1y =a −3x+3x 2(0,2]8u =+(x −)32234(0,2]x =32=u min 34=y min a 34=8a 34a =16a =16x =32(1)=log a ta 3log t ya 3t −3=y −3a log a log t log t t =a x t ≠1x =t ≠0log a x −3=−+y3x 1xlog a y =−3x +3log a x 2y =(x ≠0)a −3x+3x 2(2)u =−3x +3=+(x≠0)x 2(x −)32234y =(u≠3)a u 0<a <1y =a −3x+3x 2(0,2]8u =+(x −)32234(0,2]u (0,2]a >1y =a −3x+3x 2(0,2]8u =+(x −)32234(0,2]x =32=u min 34=y min a 34=8a 34a =16=3综上，可知所求，．22.【答案】【考点】函数解析式的求解及常用方法待定系数法求二次函数解析式二次函数的应用一元二次不等式与二次函数函数的单调性及单调区间函数最值的应用【解析】（1）结合一元二次函数的图形特征，列出与.（2）根据对称轴与区间的关系来分类讨论；（3）观察图形知在 上单调递增，求解方程即可.【解答】此题暂无解答a =16x =32−=b 2a 12Δ=02n ≤=n ≤f (x)1418m,n {f (m)=2mf (n)=2n。

2023北京首都师大附高一10月月考数 学第Ⅰ卷（共50分）一、选择题（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，选出符合题目要求的一项）1. 下列各式：①{}10,1,2∈；②{}0,1,2∅⊆；③{}{}10,1,2∈；④{}{}0,1,22,0,1=，其中错误的个数是（ ） A. 1个B. 2个C. 3个D. 4个2. 命题“2x ∃<,220x x −<”的否定是（ ） A. 2x ∃≤,220x x −≥ B. 2x ∀≥,02x << C. 2x ∃<,220x x −≥D. 2x ∀<,0x ≤或2x ≥3. 将下列多项式因式分解，结果中不含因式()2x +的是（ ） A. 224x x + B. 2312x −C. 26x x +−D. ()()228216x x −+−+4. 若集合{}{3},21,Z A xx B x x n n =<==+∈∣∣，则A B =（ ）A. ()1,1−B. ()3,3−C. {}1,1−D. {}3,1,1,3−−5. 如图，I 是全集，M 、P 、S 是I 的3个子集，则阴影部分所表示的集合是（ ）A. ()M P SB. ()M P SC. ()M P SD. ()M P S6. 已知p ：111x <+，q ：()10x x +<，则p 是q 的（ ）A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件7. 下列结论成立的是（ ） A. 若ac bc <，则a b > B. 若a b >，则22a b > C. 若a b >，则11a b< D. 若110a b<<，则0b a <<8. 设集合11,Z ,,Z 3663k k M x x k N x x k ⎧⎫⎧⎫==+∈==+∈⎨⎬⎨⎬⎩⎭⎩⎭||，则（ ） A. MNB. M NC. N MD. M N ⋂=∅9. 已知,,A B C 是三个集合，若A B B C ⋃=⋂，则一定有（ ） A. A C ⊆B. C A ⊆C. C A ≠D. A =∅10. 设()C M 表示非空集合M 中元素的个数，已知非空集合,A B .定义()(),()()()(),()()C A C B C A C B A B C B C A C A C B −≥⎧⊗=⎨−<⎩，若{}1,2A =，()(){}2220B x x ax x ax =+++=且1A B ⊗=，则实数a 的所有取值为（ ）A. 0B. 0，−C. 0，D. −，0，第Ⅱ卷（共70分）二、填空题（本大题共5小题，每小题5分，共25分）11. 方程组322327x y x y +=⎧⎨−=⎩的解集用列举法表示为______________.12. 若“25x m >−”是“|x |<1”的必要不充分条件，则实数m 的取值范围是___________ 13. 设a ，b ∈R ，集合{}2,0,1{,,0}a a b −=，则a b +的值是______.14. 已知集合{}|3A x a x =≤≤，{}|0B x x =<，若A B ⋂=∅，则实数a 的取值范围是______． 15. 当两个集合中有一个集合为另一个集合的子集时，称两个集合之间构成“全食”；当两个集合有公共元素，但互不为对方子集时，称两个集合之间构成“偏食”，对于集合11,,12A ⎧⎫=−⎨⎬⎩⎭，{}2B x x a ==|.若A 与B 构成“全食”，则a 的取值范围是______；若A 与B 构成“偏食”，则a 的取值范围是______.三、解答题（本大题共4小题，共45分.解答应写出文字说明，演算步骤或证明过程）16. 已知全集U =R ，集合{R |211}A x x =∈−≤，集合{R |12}B x x =∈−<≤． （1）求集合A B ⋂及()UA B ⋃；（2）若集合{|2,0}=∈≤<>C x R a x a a ，且C B ⊆，求实数a 的取值范围． 17. 已知关于x 的一元二次方程()22230x m x m +−+=有两个实数根1x ，2x .（1）求实数m 的取值范围； （2）若12126x x x x +=−，求m 的值.18. 已知全集U =R ，812x A xx ⎧⎫+=>⎨⎬−⎩⎭，{}22240B x x mx m =−+−<，{}14C x x =−<<，在①Ux A ∈；②x A C ∈；③x A C ∈⋃；这三个条件中任选一个补充到下列问题中并作答.问题：设p ：______，q ：x B ∈，是否存在实数m ，使得p 是q 的必要不充分条件？若实数m 存在，求m 的取值范围；若实数m 不存在，说明理由.19. 已知集合{}1,2,,A n =⋅⋅⋅（3n ≥），表示集合A 中的元素个数，当集合A 的子集i A 满足2i A =时，称i A 为集合A 的二元子集，若对集合A 的任意m 个不同的二元子集1A ，2A ，…，m A ，均存在对应的集合B 满足：①BA ⊆；②B m =；③1i BA ≤（1i m ≤≤），则称集合A 具有性质J .（1）当3n =时，若集合A 具有性质J ，请直接写出集合A 的所有二元子集以及m 的一个取值； （2）当6n =，4m =时，判断集合A 是否具有性质J ？并说明理由.参考答案第Ⅰ卷（共50分）一、选择题（本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，选出符合题目要求的一项）1. 【答案】A【分析】根据集合与集合的关系，元素与集合的关系即可求解.【详解】由元素与集合的关系可知{}10,1,2∈正确，{}{}10,1,2∈不正确， 由集合之间的关系知{}0,1,2∅⊆正确， 由集合中元素的无序性知{}{}0,1,22,0,1=正确， 故错误的个数为1， 故选：A【点睛】本题主要考查了元素与集合的关系，集合的子集，集合的相等，属于容易题. 2. 【答案】D【分析】根据存在量词命题的否定是全称量词命题即可得到结果. 【详解】命题“2x ∃<,220x x −<”是存在量词命题, 又22002x x x −<⇒<<,所以其否定为全称量词命题,即为“2x ∀<,0x ≤或2x ≥”. 故选:D. 3. 【答案】C【分析】利用提取公因式法判断A ，利用公式法判断B ，利用十字相乘法判断C 、D. 【详解】对于A.原式()22x x =+，不符合题意；对于B.原式()()()234322x x x =−=+−，不符合题意；对于C 原式()()23x x =−+，符合题意； 对于D.原式()()22242x x =−+=+，不符合题意. 故选：C. 4. 【答案】C【分析】解绝对值不等式得A ，根据交集的定义计算即可.【详解】解3x <得33x −<<，即()3,3A =−，B 为奇数集，故{}1,1A B =−.故选：C 5. 【答案】C【分析】根据Venn 图表示的集合运算作答．【详解】阴影部分在集合,M P 的公共部分，但不在集合S 内，表示为()⋂⋂M P S ， 故选：C ． 6. 【答案】D【分析】分别求出,p q ，再分析出,p q 的推导关系. 【详解】()11110010111x x x x x x −<⇒−<⇒<⇒+>+++， 所以:0p x >或1x <−，而:10q x −<<，所以p 是q 的既不充分也不必要条件， 故选：D 7. 【答案】D【分析】根据不等式的性质或举出反例对各选项逐一判断即可.【详解】选项A ：当0c >时，若ac bc <，则a b <，当0c <时，若ac bc <，则a b >，故A 说法错误； 选项B ：若1a =，2b =−满足a b >，此时22a b <，故B 说法错误； 选项C ：当0a b >>或0a b >>时， 11a b <，当0a b >>时， 11a b>，故C 说法错误；选项D ：当110a b<<时，0ab >，所以不等式同乘ab 可得0b a <<，故D 说法正确； 故选：D 8. 【答案】B【分析】根据集合,M N 的表达式，可求出集合M 是16的奇数倍，N 是16的整数倍，即可得出,M N 的关系.【详解】由()11,Z 21,Z 366k M x x k x x k k ⎧⎫⎧⎫==+∈==+∈⎨⎬⎨⎬⎩⎭⎩⎭||可知，集合M 表示的是16的奇数倍； 由()11,Z 2,Z 636k N x x k x x k k ⎧⎫⎧⎫==+∈==+∈⎨⎬⎨⎬⎩⎭⎩⎭||可知，集合N 表示的是16的整数倍； 即可知M 是N 的真子集，即M N . 故选：B 9. 【答案】A 【分析】根据()B C B ⋂⊆，以及()B C C ⋂⊆，结合已知条件，即可判断集合之间的关系. 【详解】因为()B C B ⋂⊆，又A B B C ⋃=⋂， 故可得()A B B ⋃⊆，则A B ⊆； 因为()B C C ⋂⊆，又A B B C ⋃=⋂,故可得()A B C ⋃⊆，则B C ⊆； 综上所述：A B C ⊆⊆. 故选：A.【点睛】本题考查由集合的运算结果，求集合之间的关系，属基础题. 10. 【答案】D【分析】由题意可得集合B 中的元素个数为1个或3个，分集合B 中的元素个数为1和集合B 中的元素个数为3两种情况，再结合一元次方程根的个数求解即可. 【详解】解：由2220xax x ax 可得20x ax或220x ax ++=，又因为{}1,2A =，1A B ⊗=， 所以集合B 中的元素个数为1个或3个， 当集合B 中的元素个数为1时，则20x ax有两相等的实数根，且220x ax ++=无解，所以22080a a ⎧=⎨−<⎩，解得0a =；当集合B 中的元素个数为3时，则20x ax有两不相等的实数根，且220x ax ++=有两个相等且异于方程20x ax 的根的解，所以20Δ80a a ≠⎧⎨=−=⎩，解得a =a =−综上所述，0a =或a =a =− 故选：D.【点睛】关键点睛：本题的关键是根据题意得出集合B 中的元素个数为1个或3个.第Ⅱ卷（共70分）二、填空题（本大题共5小题，每小题5分，共25分）11. 【答案】(){}3,7−【分析】首先根据方程组求出其解，然后运用列举法表示出对应的解集即可（以有序数对(),a b 的形式表示元素）.【详解】因为322327x y x y +=⎧⎨−=⎩，所以37x y =⎧⎨=−⎩，所以列举法表示解集为：(){}3,7−.故答案为(){}3,7−.【点睛】本题考查二元一次方程组解集的列举法表示，难度较易.二元一次方程组的解用列举法表示时，可将元素表示成有序数的形式：(),x y . 12. 【答案】(],2−∞【分析】根据题意得到(1,1)− (25,+)m −∞，再利用数轴得到不等式，解出不等式即可. 【详解】||<1,1<<1x x ∴−>25x m −是||1x <的必要不充分条件,(1,1)∴− (25,+)m −∞,251,2m m ∴−≤−∴≤, ∴实数m 的取值范围是(,2]−∞,故答案为： (,2]−∞. 13. 【答案】0【分析】由集合相等的含义，分类讨论元素对应关系即可. 【详解】由集合元素互异性：0a ≠，又{}2,0,1{,,0}a a b −=，则21a a b ⎧=⎨=−⎩或21a ba ⎧=⎨=−⎩，解得11a b =⎧⎨=−⎩或11a b =−⎧⎨=⎩，故0a b += 故答案为：0 14. 【答案】0a ≥【分析】分别讨论A =∅和A ≠∅两种情况求解.【详解】因为A B ⋂=∅， 若3a >，则A =∅，满足题意；若3a ≤，则应满足0a ≥，所以03a ≤≤， 综上，0a ≥. 故答案为：0a ≥.15. 【答案】 ①. {|0a a <或}1a = ②. 14⎧⎫⎨⎬⎩⎭【分析】分情况解集合B ，再根据“全食”与“偏食”的概念分析集合中元素满足的关系列式求解即可. 【详解】由{}2B x x a ==|可知，当a<0时，B =∅，此时B A ⊆； 当0a =时，{}0B =，此时A B ⋂=∅，当0a >时，{B =； 又11,,12A ⎧⎫=−⎨⎬⎩⎭，若A 与B 构成“全食”，则B A ⊆， 当a<0时，满足题意；当0a =时，不合题意；当0a >时，要使B A ⊆，则{}1,1B =−1=，解得1a =； 综上，A 与B 构成“全食”时，a 的取值范围是{|0a a <或}1a =； 若A 与B 构成“偏食”时，显然0a ≤时，不满足题意，当0a >时，由A B ⋂≠∅，所以11,22B ⎧⎫=−⎨⎬⎩⎭12=，解得14a =，此时a 的取值范围是14⎧⎫⎨⎬⎩⎭.故答案为：{|0a a <或}1a =；14⎧⎫⎨⎬⎩⎭三、解答题（本大题共4小题，共45分.解答应写出文字说明，演算步骤或证明过程）16. 【答案】（1）(1,1]A B ⋂=−，(1,)UA B ⋃=−+∞；（2）(0,1]【分析】（1）解一元一次不等式求集合A ，再应用集合的交并补运算求A B ⋂及()UA B ⋃.（2）由集合的包含关系可得2a ≤2，结合已知即可得a 的取值范围． 【小问1详解】由211x −≤得：1x ≤，所以(,1]A ∞=−，则(1,)UA =+∞，由(1,2]B =−，所以(1,1]A B ⋂=−，(1,)UA B ⋃=−+∞．【小问2详解】 因为C B ⊆且0a >， 所以2a ≤2，解得1a ≤． 所以a 的取值范围是(0,1]． 17. 【答案】（1）34m ≤ （2）1m =−【分析】（1）根据根的判别式列不等式，然后解不等式即可；（2）根据韦达定理得到1223x x m +=−+，212x x m =，然后代入求解即可.【小问1详解】因为有两个实根，所以()222341290m m m ∆=−−=−+≥，解得34m ≤. 【小问2详解】由题意得()122323x x m m +=−−=−+，212x x m =，所以2236m m −+=−，整理得 ()()310m m −+=，解得3m =或-1，因为34m ≤，所以1m =−. 18. 【答案】答案见解析【分析】分别求解集合,A B ，并求解三个条件的集合，再根据必要不充分条件，转化为集合的包含关系，即可列式求解. 【详解】不等式8831100222x x x x x x +++>⇔−>⇔<−−−，即()()320x x +−<， 解得：32x −<<，即{}32A x x =−<<，()()22240220x mx m x m x m −+−<⇔−−−+<⎡⎤⎡⎤⎣⎦⎣⎦，解得：22m x m −<<+，即{}22B x m x m =−<<+， 若选①，{3UA x x =≤−或2}x ≥，:p {3U x A x x ∈=≤−或2}x ≥，{}:22q x B x m x m ∈=−<<+，若p 是q 的必要不充分条件，则BUA ,即23m +≤−或22m −≥，解得：5m ≤−或4m ≥；所以存在实数m ，使得p 是q 的必要不充分条件，m 的范围为5m ≤−或4m ≥； 若选②，{}12A C x x ⋂=−<<，:p {}12x A C x x ∈⋂=−<<，{}:22q x B x m x m ∈=−<<+，若p 是q 的必要不充分条件，则B ()A C ,则2122m m −≥−⎧⎨+≤⎩，解集为∅；所以不存在实数m ，使得p 是q 的必要不充分条件； 若选③，{}34A C x x ⋃=−<<，:p {}34x A C x x ∈⋃=−<<，{}:22q x B x m x m ∈=−<<+，若p 是q 的必要不充分条件，则B ()A C ,则2324m m −≥−⎧⎨+≤⎩，解得：12m −≤≤；所以存在实数m ，使得p 是q 的必要不充分条件，m 的取值范围为12m −≤≤； 19. 【答案】（1）答案见解析 （2）不具有，理由见解析【分析】（1）根据集合A 具有性质J 的定义即可得出答案；（2）当6n =，4m =时，利用反证法即可得出结论. 【小问1详解】当3n =时，{}1,2,3A =，集合A 的所有二元子集为{}{}{}1,2,1,3,2,3，则满足题意得集合B 可以是{}1或{}2或{}3，此时1m =， 或者也可以是{}1,2或{}1,3或{}2,3，此时2m =； 【小问2详解】当6n =，4m =时，{}1,2,3,4,5,6A =，假设存在集合B ，即对任意的()1234,,,,4,114i A A A A B B A i =⋂≤≤≤，则取{}{}{}{}12341,2,3,4,5,6,2,3A A A A ====，（4A 任意构造，符合题意即可） 此时由于4B =，由抽屉原理可知，必有()223i B A i ⋂=≤≤， 与题设矛盾，假设不成立， 所以集合A 是不具有性质J .【点睛】关键点点睛：此题对学生的抽象思维能力要求较高，特别是对数的分析，在解题时注意对新概念的理解与把握是解题的关键.。

2022-2023学年全国高一上数学月考试卷考试总分：110 分 考试时间： 120 分钟学校：__________ 班级：__________ 姓名：__________ 考号：__________注意事项：1．答题前填写好自己的姓名、班级、考号等信息; 2．请将答案正确填写在答题卡上;卷I （选择题）一、 选择题 （本题共计 12 小题 ，每题 5 分 ，共计60分 ）1. 设全集，集合，，则图中阴影部分所表示的集合为( )A.B.C.D.2. 下列复数中实部与虚部互为相反数的是( )A.B.C.D.3. 已知平面向量，的夹角为，且，则的最小值为（ ）A.B.C.D.4. 临近学期结束，某中学要对本校高中部一线科任教师进行“评教评学”调査，经调査，高一年级U =R A ={x|(x +1)(x −3)<0}B ={x|x −1≥0}{x|x ≤−1或x ≥3}{x|x <1或x ≥3}{x|x ≤1}{x|x ≤−1}2−i(1−i)2i (1+i)i (1−2i)a →b →120∘⋅=−1a →b →|−|a →b →6–√3–√2–√190%92%名一线科任教师好评率为，高二年级名一线科任教师好评率为，高三年级名一线科任教师好评率为．依此估计该中学高中部一线科任教师的好评率约为（ ）A.B.C.D.5. 不论为何实数，直线恒过定点( )A.B.C.D.6. 某人向正东方向走后，向右转，然后朝新方向走，结果他恰好离出发地，那么的值为（ ）A.B.C.或D.7. 设是定义在上的奇函数，且满足 ，当时，，则（ ）A.B.C.D.8. 袋中有个小球（白黑），现从袋中每次取一个球，不放回地抽取两次，则在第一次取到白球的条件下，第二次取到白球的概率是（ ）A.8090%7592%8095%92%93%94%95%m (m −1)x −y −2m +1=0(1,−1)（2,−1）(−2,−1)(1,1)x km 150∘ 3 km km 3–√x 3–√23–√3–√23–√5f (x)R f (x +2)=−f (x)0≤x ≤1f (x)=x (1+x)f (−)=92−34−141434532353B.C.D.9. 若双曲线的一条渐近线被圆所截得的弦长为，则的渐近线方程为( )A.B. C. D.10. 已知函数＝是奇函数，直线与函数的图象的两个相邻交点的横坐标之差的绝对值为，则（ ）A.在上单调递减B.在上单调递减C.在上单调递增D.在上单调递增11. 已知正方体的棱长为，，分别是棱，的中点，动点在正方形（包括边界）内运动，若面，则线段的长度范围是( )A.3412310C :−=1(a >0,b >0)x 2a 2y 2b 2+=2x 2(y −2)22C y =±x 3–√3y =±x 21−−√7y =±x 21−−√3y =±x3–√f(x)sin(ωx +φ)+cos(ωx +φ)(ω>0,0<φ<π)y =2–√f(x)π2f(x)(0,)π4f(x)(,)π83π8f(x)(0,)π4f(x)(,)π83π8ABCD −A 1B 1C 1D 12M N BC CC 1P BCC 1B 1P //A 1AMN PA 1[2,]5–√[2,3]B.C.D.12. 下列不等关系中，正确的一个是( )A.B.C.D.卷II （非选择题）二、 填空题 （本题共计 4 小题 ，每题 5 分 ，共计20分 ）13. 若等比数列的各项都是正数，且，则________．14. 在正方体中，点为正方形的中心，则异面直线与所成角为________． 15. 填空13.在的展开式中的系数为________.14.已知实数，满足约束条件，则的最大系数为________.15.已知正三棱锥P-ABC 的底面边长为3，外接球的表面积为16π，则正三棱锥P-ABC 的体积为________.16.如图，过抛物线的焦点作两条互相垂直的弦、，若△ACF 与△BDF 面积之和的最小值为16，则抛物线的方程为______.[2,3][,3]32–√2[,]32–√25–√<0.7−π0.7−32<log 13log 312<0.8−0.18−0.2>0.4−23413{}a n +=16a 5a 6a 4a 7++⋯+=log 2a 1log 2a 2log 2a 10ABCD −D A 1B 1C 1E ABCD E A 1D B 1(2−)x 21x 71xx y x +y ≤0，5x +2y ≥11，y ≥x +1,12z =2x −y =2px(p >0)y 2F AB CD16. 已知定义在上的奇函数满足当时，，则不等式的解集为________.三、 解答题 （本题共计 6 小题 ，每题 5 分 ，共计30分 ）17. 在中，角，，的对边分别为，，，若，且 . 求角的值；若，且的面积为，求边上的中线的长． 18. 某射击运动员射击一次所得环数的分布列如下：现进行两次射击，以该运动员两次射击所得的最高环数作为他的成绩，记为．求该运动员两次都命中环的概率；求的分布列及数学期望．19. 已知数列中，，，前项和为，若，且.求数列的通项公式;记，求数列的前项和. 20. 如图所示，在直角梯形中，，，，，，边上一点满足．现将沿折起到的位置，使平面平面，如图所示．求证：；求平面与平面所成锐二面角的余弦值．R f (x)x ≥0f (x)=−+−1x −√e −2x f(2−10x)+f(−6x −12)<0x 2x 2△ABC A B C a b c a sin B cos C +c sin B cos A =b 12c >b (1)B (2)A =π6△ABC 43–√BC AM X X 0−678910P 00.20.30.30.2ξ(1)7(2)ξE(ξ){}a n =1a 1>0a n n S n =+(n ∈a n S n −−√S n−1−−−−√N ∗n ≥2)(1)a n (2)=⋅c n a n 2a n {}c n n T n 1ABCD BC//AD AD ⊥CD BC =2AD =3CD =3–√AD E DE =1△ABE BE △BE A 1BE ⊥A 1BCDE 2(1)C ⊥BE A 1(2)BE A 1CD A 1C :=2px (p >0)221. 已知抛物线的焦点为，为抛物线上异于原点的任意一点，过点的直线交抛物线于另一点，交轴的正半轴于点，且有.当点的横坐标为时， .求抛物线的方程；若直线，且和抛物线有且只有一个公共点，试问直线（为抛物线上异于原点的任意一点）是否过定点，若过定点，求出定点坐标；若不过定点，请说明理由． 22. 已知函数，其中是自然对数的底数．判断函数在区间上的单调性，并求最小值；设，证明：函数在区间上有唯一零点．C :=2px (p >0)y 2F A C A l C B x D |FA|=|FD|A 3|FA|=4(1)C (2)//l l 1l 1C E AE A C f (x)=x +−sin x 12e −x e =2.718281…(1)f (x)[π,]3π2(2)g(x)=x +2−f (x)12e −x g(x)(,2π)3π2参考答案与试题解析2022-2023学年全国高一上数学月考试卷一、 选择题 （本题共计 12 小题 ，每题 5 分 ，共计60分 ）1.【答案】D【考点】Venn 图表达集合的关系及运算【解析】由阴影部分表示的集合为，然后根据集合的运算即可．【解答】解：由图象可知阴影部分对应的集合为，∵，，∴，则.故选.2.【答案】C【考点】复数的基本概念复数代数形式的乘除运算【解析】本题考查复数的实部与虚部，考查运算求解能力 .【解答】解：因为，所以的实部与虚部互为相反数．故选 .3.【答案】(A ∪B)∁U (A ∪B)∁U A ={x|(x +1)(x −3)<0}=(−1,3)B ={x|x −1≥0}=[1,+∞)A ∪B =(−1,+∞)(A ∪B)=(−∞,−1]∁U D i(1+i)=−1+i i(1+i)CA【考点】数量积表示两个向量的夹角平面向量数量积向量的模【解析】根据平面向量的数量积的应用，利用基本不等式即可求解．【解答】解：∵平面向量，的夹角为，∴，∴，则，当且仅当时取等号，故的最小值为，故选．4.【答案】A【考点】用样本的数字特征估计总体的数字特征【解析】由题意计算加权平均数，即可得出结果．【解答】由题意，计算＝；依此估计该中学高中部一线科任教师的好评率约为．5.a →b →120∘⋅=||⋅||cos =−⋅||⋅||=−1a →b →a →b →120∘12a →b →||⋅||=2a →b →|−|=a →b →(−a →b →)2−−−−−−−−√=|−2⋅+|a →|2a →b →b →|2−−−−−−−−−−−−−−−−−−−√=|+|+2a →|2b →|2−−−−−−−−−−−−−−−√≥==2||⋅||+2a →b →−−−−−−−−−−−−−−√4+2−−−−√6–√||=||=a →b →2–√|−|a →b →6–√A ×(80×90%+75×92%+80×95%)≈0.92180+75+8092%92%B【考点】直线恒过定点直线的一般式方程【解析】题中函数可化为,当时，，所以该直线恒过点【解答】解：直线可化为，当时，，所以该直线恒过点.故选.6.【答案】C【考点】解三角形的实际应用【解析】此题暂无解析【解答】解：由题意得，解得或．故选．7.【答案】A【考点】函数奇偶性的性质y =(m −1)x −2m +1=(m −1)x −2(m −1)−1=(m −1)(x −2)−1x =2y =−1(2,−1)y =(m −1)x −2m +1=(m −1)x −2(m −1)−1=(m −1)(x −2)−1x =2y =−1(2,−1)B (=+−2×3x cos 3–√)232x 230∘x =3–√23–√C【解析】首先由对称得到，再结合已知函数求值即可.【解答】解：由，得，所以.又为定义在上的奇函数，所以.因为当时，，所以，所以.故选.8.【答案】C【考点】条件概率与独立事件【解析】在第一次取到白球的条件下，第二次取到白球，是一个条件概率，需要做出第一次取到白球的概率和两次都取到白球的概率，根据条件概率的公式，代入数据得到结果．【解答】解：记事件为“第一次取到白球”，事件为“第二次取到白球”，则事件为“两次都取到白球”，依题意知，，∴在第一次取到白球的条件下，第二次取到白球的概率是．故选9.【答案】f (−)=f (−)=−f ()921212f (x +2)=−f (x)f (x)=−f (x +2)f (−)92=−f (−)52=f (−)12f (x)R f (−)12=−f ()120≤x ≤1f (x)=x (1+x)f ()12=×(1+)1212=34f (−)92=−f ()12=−34A AB AB P(A)=35P(AB)=×=3524310P(B |A)==3103512CD【考点】双曲线的渐近线点到直线的距离公式【解析】本题考查双曲线的渐近线方程，直线与圆的位置关系，点到直线的距离公式，解题的关键是熟练掌握栓曲线的性质，由题意，得出栓曲线渐近线方程的表达式，再利用点到直线的距离和勾股定理即可解答本题.【解答】解：由题意，双曲线的渐近线方程为，∵双曲线的一条渐近线被圆所截得的弦长为，∴圆心到直线的距离为：，则由勾股定理得：，解得：，则，∴双曲线的渐近线方程为.故选.10.【答案】D【考点】两角和与差的正弦公式三角函数中的恒等变换应用正弦函数的单调性正弦函数的图象【解析】根据两角和的正弦函数化简解析式，由条件和诱导公式求出的值，由条件和周期共识求出的值，根据正弦函数的单调性和选项判断即可．【解答】解：由题意得，＝y =±x b a +(y −2=2x 2)22(0,2)y =±x b a 2a +a 2b 2−−−−−−√+(=2122a+a 2b 2−−−−−−√)2=3b 2a 2=b a 3–√C y =±x 3–√D φωf(x)sin(ωx +φ)+cos(ωx +φ)=[sin(ωx +φ)+cos(ωx +φ)]2–√2–√22–√2，∵函数是奇函数，∴，则，又，∴，∴，∵与的图象的两个相邻交点的横坐标之差的绝对值为，∴，则＝，即，由得，则在上不是单调函数，排除、；由得，则在上是增函数，排除，故选.11.【答案】D【考点】点、线、面间的距离计算【解析】首先确定点的轨迹，再结合正方体，确定直线的范围即可.【解答】解：取， 中点，，连接，，如图所示，则，.因为，，所以平面平面.又因为动点在正方形（包括边界）内运动，所以点的轨迹为线段.因为正方体的棱长为，所以，，所以为等腰三角形，故当点在点或者在点处时，此时最大，最大值为，当点为中点时，最小，=sin(ωx +φ+)2–√π4f(x)(ω>0,0<φ<π)φ+=kπ(k ∈Z)π4φ=−+kπ(k ∈Z)π40<φ<πφ=3π4f(x)=sin(ωx ++)=−sin ωx 2–√3π4π42–√y =2–√f(x)π2T ==2πωπ2ω4f(x)=−sin 4x 2–√x ∈(0,)π44x ∈(0,π)f(x)(0,)π4A C x ∈(,)π83π84x ∈(,)π23π2f(x)(,)π83π8B D P B 1C 1B B 1E F E A 1F A 1E//AM A 1EF//MN E ∩EF =E A 1AM ∩NM =M EF//A 1AMN P BCC 1B 1P EF ABCD −A 1B 1C 1D 12E =F =A 1A 15–√EF =2–√△EF A 1P E P F PA 15–√P EF PA 1最小值为，故线段的长度范围是.故选.12.【答案】D【考点】对数值大小的比较对数的运算性质指数函数的性质有理数指数幂的化简求值【解析】.【解答】解：，设函数，则函数在上单调递减，又，则，故错误；，由对数的运算可知，，故错误；，由，，得，故错误；，，又，则，故正确.故选.二、 填空题 （本题共计 4 小题 ，每题 5 分 ，共计20分 ）13.【答案】【考点】等比数列的性质对数的运算性质【解析】由等比数列的性质可知，可求，代入可=−()5–√2()2–√22−−−−−−−−−−−−−−√32–√2PA 1[,]32–√25–√D A y =0.7x y R −π<−3>0.7−π0.7−3A B 2=−2=log 13log 3log 312B C >10.8−0.10<<18−0.2>0.8−0.18−0.2C D ==0.4−23 2.523 6.25136.25>4>0.4−23413D D 15+=2a a a a a a a a ++⋯+log a log a log a求．【解答】解：因为，所以，则．故答案为：．14.【答案】【考点】异面直线及其所成的角【解析】解：如图所示：连结、，则、的交点，连结，由正方体的性质易得，，又因为，所以面，所以，故，即异面直线与所成角为．故答案为：．【解答】解：如图所示：连结、，则、的交点，连结，由正方体的性质易得，，又因为，所以面，所以，故，即异面直线与所成角为．故答案为：．15.【答案】-842或【考点】二项式系数的性质球内接多面体222+=2=16a 5a 6a 4a 7a 5a 6=8a 5a 6++…+log 2a 1log 2a 2log 2a 10=(⋯)log 2a 1a 2a 10=log 2()a 5a 65=1515π2BD AC BD AC E E A 1A ⊥BD A 1AC ⊥BD A ∩AC =A A 1BD ⊥AE A 1BD ⊥E A 1⊥E B 1D 1A 1E A 1B 1D 1π2π2BD AC BD AC E E A 1A ⊥BD A 1AC ⊥BD A ∩AC =A A 1BD ⊥AE A 1BD ⊥E A 1⊥E B 1D 1A 1E A 1B 1D 1π2π233–√493–√4=4xy 22–√同余【解析】此题暂无解析【解答】解：解：解：解：16.【答案】【考点】奇偶性与单调性的综合函数奇偶性的性质函数单调性的性质利用导数研究函数的单调性【解析】由已知求得函数解析式，再由导数研究函数的单调性，把转化为关于的一元二次不等式求解．【解答】解：时，，，时，，，，，，，在上为减函数，，且为上的奇函数，可得图象关于对称，且在上为一连续不间断的曲线，在上为减函数，且，化为，为上减函数，(−∞,−)∪(6,+∞)23f (2−10x)−f (−6x −12)<0x 2x 2x ∵x ≥0f (x)=−+−1x −√e −2x (x)=−⋅−2=−(+2)(x >0)f ′121x −√e −2x 12x −√e −2x ∵x >0>012x −√−2x <0∈(0,1)e −2x ∴+>012x −√e −2x∴−(+)<012x −√e −2x ∴(x)<0f ′∴f (x)(0,+∞)∵f (0)=−+−1=1−1=00–√e 0f (x)R ∴f (x)(0,0)R ∴f (x)R f (−x)=−f (x)∴f (2−10x)+f (−6x −12)<0x 2x 2f(2−10x)<−f(−6x −12)=f(−+6x +12)x 2x 2x 2∵f (x)R，即 ，解得或， 解集为 ．故答案为：．三、 解答题 （本题共计 6 小题 ，每题 5 分 ，共计30分 ）17.【答案】解：∵，由正弦定理得，∵，，∴，即，得 .又，∴，∴ .由知，若，故，则，∴，（舍），又在中， ，∴，∴ .【考点】两角和与差的正弦公式正弦定理余弦定理解三角形【解析】此题暂无解析【解答】∴2−10x >−+6x +12x 2x 23−16x −12>0x 2x <−23x >6∴(−∞,−)∪(6,+∞)23(−∞,−)∪(6,+∞)23(1)a sin B cos C +c sin B cos A =b 12sin A sin B cos C +sin C sin B cos A =sin B 12B ∈(0,π)sin B ≠0sin A cos C +sin C cos A =12sin(A +C)=12sin B =12c >b 0<B <π2B =π6(2)(1)B =π6A =π6a =b =ab sin C =sin =4S △ABC1212a 22π33–√a =4a =−4△AMC A =A +M −2AC ⋅MC cos M 2C 2C 22π3A =A +−2⋅AC ⋅AC ⋅cos M 2C 2(AC)122122π3=+−2×4×2×(−)=28422212AM =27–√解：∵，由正弦定理得，∵，，∴，即，得 . 又，∴，∴ . 由知，若，故，则，∴，（舍），又在中， ，∴，∴ .18.【答案】解：设“该运动员两次都命中环”为事件，则．可取、、、，则，，，，故的分布列为．【考点】古典概型及其概率计算公式离散型随机变量的期望与方差离散型随机变量及其分布列【解析】根据相互独立事件概率公式计算；根据相互独立事件概率公式求出的分布列，再计算．【解答】(1)a sin B cos C +c sin B cos A =b 12sin A sin B cos C +sin C sin B cos A =sin B 12B ∈(0,π)sin B ≠0sin A cos C +sin C cos A =12sin(A +C)=12sin B =12c >b 0<B <π2B =π6(2)(1)B =π6A =π6a =b =ab sin C =sin =4S △ABC 1212a 22π33–√a =4a =−4△AMC A =A +M −2AC ⋅MC cos M 2C 2C 22π3A =A +−2⋅AC ⋅AC ⋅cos M 2C 2(AC)122122π3=+−2×4×2×(−)=28422212AM =27–√(1)7A P(A)=0.2×0.2=0.04(2)ξ78910P (ξ=7)=0.04P (ξ=8)=2×0.2×0.3+=0.210.32P(ξ=9)=0.5×0.3×2+=0.390.32P(ξ=10)=0.2×0.8×2+=0.360.22ξξ78910P 0.040.210.390.36∴E (ξ)=7×0.04+8×0.21+9×0.39+10×0.36=9.07(1)(2)ξE(ξ)解：设“该运动员两次都命中环”为事件，则．可取、、、，则，，，，故的分布列为．19.【答案】解：在数列中，∵且，∴①式÷②式得：∴数列是以为首项，公差为的等差数列，∴，∴.当时，，当时，，也满足上式，∴数列的通项公式为.由知，，∴，则，，得，，(1)7A P(A)=0.2×0.2=0.04(2)ξ78910P (ξ=7)=0.04P (ξ=8)=2×0.2×0.3+=0.210.32P(ξ=9)=0.5×0.3×2+=0.390.32P(ξ=10)=0.2×0.8×2+=0.360.22ξξ78910P 0.040.210.390.36∴E (ξ)=7×0.04+8×0.21+9×0.39+10×0.36=9.07(1){}a n =−(n ≥2)①a n S n S n−1=+②a n S n −−√S n−1−−−−√>0a n −=1(n ≥2)S n −−√S n−1−−−−√{}S n −−√==1S 1−−√a 1−−√1=1+(n −1)=nS n −−√=S n n 2n ≥2=−a n S n S n−1=−(n −1=2n −1n 2)2n =1=1a 1{}a n =2n −1a n (2)(1)=2n −1a n =(2n −1)⋅c n 22n−1=1⋅2+3⋅+5⋅+⋯T n 2325+(2n −1)⋅①22n−14=1⋅+3⋅+5⋅+⋯T n 232527+(2n −3)⋅+(2n −1)⋅②22n−122n+1①−②−3=2+2(++…T n 2325+)−22n−1(2n −1)22n+1=2+2−(2n −1)8(1−)22n−21−422n+1=−+(−2n)1035322n+1【考点】数列的求和数列递推式等差数列的通项公式【解析】此题暂无解析【解答】解：在数列中，∵且，∴①式÷②式得：∴数列是以为首项，公差为的等差数列，∴，∴.当时，，当时，，也满足上式，∴数列的通项公式为.由知，，∴，则，，得，，(1){}a n =−(n ≥2)①a n S n S n−1=+②a n S n −−√S n−1−−−−√>0a n −=1(n ≥2)S n −−√S n−1−−−−√{}S n −−√==1S 1−−√a 1−−√1=1+(n −1)=n S n −−√=S n n 2n ≥2=−a n S n S n−1=−(n −1=2n −1n 2)2n =1=1a 1{}a n =2n −1a n (2)(1)=2n −1a n =(2n −1)⋅c n 22n−1=1⋅2+3⋅+5⋅+⋯T n 2325+(2n −1)⋅①22n−14=1⋅+3⋅+5⋅+⋯T n 232527+(2n −3)⋅+(2n −1)⋅②22n−122n+1①−②−3=2+2(++…T n 2325+)−22n−1(2n −1)22n+1=2+2−(2n −1)8(1−)22n−21−422n+1=−+(−2n)1035322n+120.【答案】证明：在图中，连接，易求，∴四边形为菱形．连接交于点，如图，则．∴在图中，，．又，∴平面．又平面，∴．解：在图中延长，，设，连接．∵平面，平面，又平面，平面，∴是平面与平面的交线．∵平面平面，，平面平面，∴平面 ．又平面，∴．作，垂足为，连接．又，∴面，又平面，∴．∴即为平面与平面所成锐二面角的平面角．由知，，为等边三角形，∴．∵，∴，解得．在中，．∴，∴平面与平面所成锐二面角的余弦值为．(1)1CE CE =BC =BE =AE =AB =2ABCE AC BE O AC ⊥BE 2O ⊥BE A 1OC ⊥BE O ∩OC =O A 1BE ⊥OC A 1C ⊂A 1OC A 1C ⊥BE A 1(2)2BE CD BE ∩CD =G G A 1G ∈BE A 1G ∈CD A 1∈A 1BE A 1∈A 1CD A 1G A 1BE A 1CD A 1BE ⊥A 1BCDE OC ⊥BE BE∩A 1BCDE =BE OC ⊥BE A 1G ⊂A 1BE A 1OC ⊥G A 1OH ⊥G A 1H CH OH ∩OC =O G ⊥A 1OCH CH ⊂OCH G ⊥CH A 1∠OHC BE A 1CD A 1(1)△BE A 1△BCE OC =3–√△OHG ∼△B G A 1==OH BA 1OG BG 34OH =32Rt △COH CH =O +O C 2H 2−−−−−−−−−−√==3+94−−−−−√21−−√2cos ∠OHC ===OH CH 3221√221−−√7BE A 1CD A 121−−√7【考点】直线与平面垂直的判定直线与平面垂直的性质二面角的平面角及求法【解析】无无【解答】证明：在图中，连接，易求，∴四边形为菱形．连接交于点，如图，则．∴在图中，，．又，∴平面．又平面，∴．解：在图中延长，，设，连接．∵平面，平面，又平面，平面，∴是平面与平面的交线．∵平面平面，，平面平面，∴平面 ．又平面，∴．作，垂足为，连接．又，∴面，又平面，∴．∴即为平面与平面所成锐二面角的平面角．由知，，为等边三角形，∴．∵，(1)1CE CE =BC =BE =AE =AB =2ABCE AC BE O AC ⊥BE 2O ⊥BE A 1OC ⊥BE O ∩OC =O A 1BE ⊥OC A 1C ⊂A 1OC A 1C ⊥BE A 1(2)2BE CD BE ∩CD =G G A 1G ∈BE A 1G ∈CD A 1∈A 1BE A 1∈A 1CD A 1G A 1BE A 1CD A 1BE ⊥A 1BCDE OC ⊥BE BE∩A 1BCDE =BE OC ⊥BE A 1G ⊂A 1BE A 1OC ⊥G A 1OH ⊥G A 1H CH OH ∩OC =O G ⊥A 1OCH CH ⊂OCH G ⊥CH A 1∠OHC BE A 1CD A 1(1)△BE A 1△BCE OC =3–√△OHG ∼△B G A 1=OH OG 3H =3∴，解得．在中，．∴，∴平面与平面所成锐二面角的余弦值为．21.【答案】解：由题意知，由抛物线的定义知：，解得，所以抛物线的方程为.由知，设，,因为，所以，由得，故，故直线的斜率为，因为直线和直线平行，故可设直线的方程为，代入抛物线方程得,由题意知，得,设，则，，当时，,可得直线的方程为,由，整理可得,所以直线恒过点,当时，直线的方程为，过点，所以直线恒过定点.【考点】抛物线的标准方程直线与抛物线的位置关系圆锥曲线中的定点与定值问题==OH BA 1OG BG 34OH =32Rt △COH CH =O +O C 2H 2−−−−−−−−−−√==3+94−−−−−√21−−√2cos ∠OHC ===OH CH 3221√221−−√7BE A 1CD A 121−−√7(1)F (,0)p23+=4p 2p =2C =4x y 2(2)(1)F (1,0)A (,)(>0)x 0y 0x 0D (,0)(>0)x D x D |FA|=|FD||−1|=+1x D x 0>0x D =+2x D x 0D (+2,0)x 0AB =−k AB y 02l 1AB l 1y =−x +b y 02+y −=0y 28y 08b y 0Δ=+=064y 2032b y 0b =−2y 0E (,)x E y E =−y E 4y 0=x E 4y 20≠4y 20==k AE −y E y 0−x E x 04y 0−4y 20AE y −=(x −)y 04y 0−4y 20x 0=4y 20x 0y =(x −1)4y 0−4y 20AE F (1,0)=4y 20AE x =1F (1,0)AE F (1,0)【解析】（1）由题意知，由抛物线的定义知：，求出,即可得解抛物线的方程为由（）知，设,根据已知条件可得即,即可得到直线的斜率为，根据直线和直线平行，可设直线的方程为,联立抛物线方程即可得到，再分和分类讨论求解直线的方程，即可得解直线恒过定点.【解答】解：由题意知，由抛物线的定义知：，解得，所以抛物线的方程为.由知，设，,因为，所以，由得，故，故直线的斜率为，因为直线和直线平行，故可设直线的方程为，代入抛物线方程得,由题意知，得,设，则，，当时，,可得直线的方程为,由，整理可得,所以直线恒过点,当时，直线的方程为，过点，所以直线恒过定点.22.【答案】解：由已知可得， ，当时， ，F (,0)p 23+=4p 2p =2C =4x.y 2(Ⅱ)ⅠF (1,0)A (,)(>0),D (,)(>0)x 0y 0x 0x D y 0x D =+2,x D x 0D (+2,0)x 0AB =−k AB y 02l 1AB l 1y =−x +b y 02=−,=y E 4y 0x E 4y 20≠4y 20=4y 20AE AE F (1,0)(1)F (,0)p 23+=4p 2p =2C =4x y 2(2)(1)F (1,0)A (,)(>0)x 0y 0x 0D (,0)(>0)x D x D |FA|=|FD||−1|=+1x D x 0>0x D =+2x D x 0D (+2,0)x 0AB =−k AB y 02l 1AB l 1y =−x +b y 02+y −=0y 28y 08b y 0Δ=+=064y 2032b y 0b =−2y 0E (,)x E y E =−y E 4y 0=x E 4y 20≠4y 20==k AE −y E y 0−x E x 04y 0−4y 20AE y −=(x −)y 04y 0−4y 20x 0=4y 20x 0y =(x −1)4y 0−4y 20AE F (1,0)=4y 20AE x =1F (1,0)AE F (1,0)(1)(x)=−−cos x f ′12e −x x ∈[π,]3π2−1≤cos x ≤0x)=−−cos x ≥−>01x 1x所以，所以在区间上是单调递增的，故函数在上的最小值为．证明：由已知条件可知：，当时， ，，所以在区间上是单调递增的.又，，所以存在唯一的，使得，所以时，，函数单调递减，时，，函数单调递增.因为，所以函数在区间上没有零点.因为，，所以函数在区间上存在唯一零点，故函数在区间上有唯一零点．【考点】利用导数研究函数的单调性利用导数研究函数的最值利用导数研究与函数零点有关的问题【解析】此题暂无解析【解答】解：由已知可得， ，当时， ，所以，所以在区间上是单调递增的，故函数在上的最小值为．证明：由已知条件可知：，(x)=−−cos x ≥−>0f ′12e −x 12e −x f (x)[π,]3π2[π,]3π2f (π)=+π2e −π(2)g(x)=+sin x e −x x ∈(,2π)3π2(x)=−+cos x g ′e −x (x)=−sin x >0g ′′e −x (x)g ′(,2π)3π2()=−<0g ′3π2e −3π2(2π)=−+1>0g ′e −2πt ∈(,2π)3π2(t)=0g ′x ∈(,t)3π2(x)<0g ′g(x)x ∈(t,2π)(x)>0g ′g(x)g()=−1<03π2e −3π2g(x)(,t)3π2g(t)<g()<03π2g(2π)=>0e −2πg(x)(t,2π)g(x)(,2π)3π2(1)(x)=−−cos x f ′12e −x x ∈[π,]3π2−1≤cos x ≤0(x)=−−cos x ≥−>0f ′12e −x 12e −xf (x)[π,]3π2[π,]3π2f (π)=+π2e −π(2)g(x)=+sin x e −x ∈(,2π)3π当时， ，，所以在区间上是单调递增的.又，，所以存在唯一的，使得，所以时，，函数单调递减，时， ，函数单调递增.因为，所以函数在区间上没有零点.因为，，所以函数在区间上存在唯一零点，故函数在区间上有唯一零点．x ∈(,2π)3π2(x)=−+cos x g ′e −x (x)=−sin x >0g ′′e −x (x)g ′(,2π)3π2()=−<0g ′3π2e −3π2(2π)=−+1>0g ′e −2πt ∈(,2π)3π2(t)=0g ′x ∈(,t)3π2(x)<0g ′g(x)x ∈(t,2π)(x)>0g ′g(x)g()=−1<03π2e −3π2g(x)(,t)3π2g(t)<g()<03π2g(2π)=>0e −2πg(x)(t,2π)g(x)(,2π)3π2。

高一年级上学期第一次月考数学试卷一、选择题（本小题共12小题，每小题4分，共48分，在每小题给出的四个选项中，只有一项是符合题目要求）1．已知集合A={1，2，4，6}，B ＝{1}，则A ∪B 等于（ ）A ．{1，2，4，6}B ．{2，4，6}C ．{0，2，6}D ．Φ3．设1(1)()3(1)x x f x x x +≥⎧=⎨-<⎩，则((1))f f -的值为（ ）A.1-B.5C.52D.4 4．下列各组函数中，表示同一函数的是（ ） A ．xxy y ==,1 B ．1,112-=+⨯-=x y x x y C ．33,x y x y == D ． 2)(|,|x y x y ==5．已知()x f 是偶函数，且()54=f ，那么()()44-+f f 的值为（ ）A ．5B ．10C ．8D ．不确定6．已知关于x 的方程5x 2+k x －6=0的一个根为2，设方程的另一个根为x 1，则有（ ）A ．x 1=53，k=-7 B ．x 1=-53，k=-7 C ．x 1=-53，k=7 D ．x 1=53，k=77．如果函数()x f =x 2+2(a －1)x +2在区间(－∞，4)上是减函数，则实数a 的取值范围是（ ）A ．a ≥－3 B. a ≤5 C. a ≤－3 D. a ≥58．函数y=3232+-x x 的值域是 （ ） A ．(－∞，－1 )∪(－1，＋∞) B ．(－∞，1)∪(1，＋∞) C ．(－∞，0 )∪(0，＋∞)D ．(－∞，0)∪(1，＋∞)9．函数()f x =）A ．3,2⎛⎤-∞ ⎥⎝⎦B ．31,2⎡⎤-⎢⎥⎣⎦C ．3,2⎡⎫+∞⎪⎢⎣⎭D ．3,42⎡⎤⎢⎥⎣⎦10．已知函数()533f x ax bx cx =-+-，()37f -=，则()3f 的值 ( )A . 13- B. 13 C.7 D. 7- 11．下列四个命题（1）f(x )=x x -+-12是函数; （2）函数是其定义域到值域的映射;（3）函数y=2x (x N ∈)的图象是一直线；（4）函数y=⎪⎩⎪⎨⎧<-≥0,0,22x x x x 的图象是抛物线，其中正确的命题个数是（ ）A ．1B ．2C ．3D ．412．已知函数)(x f 是R 上的增函数，(0,2)-A ，(3,2)B 是其图象上的两点，那么2|)1(|<+x f 的解集是（ ）A ．（1，4）B ．（-1，2）C ．),4[)1,(+∞-∞D ．),2[)1,(+∞--∞ 二．填空题（4×4=16分） 13．函数y11x -的定义域是 . 14．函数[]225(1,2)y x x x =-+∈-的最大值是________,最小值是_________. 15．设f (x －1)=3x －1，则f (x )= . 16．已知函数842++-=m mx mx y 的定义域为R,则实数m 的范围为_________.三．解答题（共6小题，共56分）17．（8分）已知集合A={}13x x <<，集合B={}12x x x <->或，求,A B A B ⋂⋃18. (8分)已知y =f (x )是一次函数，且有f [f (x )]=9x ＋8，求此一次函数的解析式. 19．（10分）（1）画出函数y ＝－x 2＋2|x |＋3的图象，并指出函数的单调区间．（2）不等式－x 2＋2|x |＋3<m 恒成立，求m 的取值范围20．（10分）解关于x 的不等式2(1)0x a x a -++>21．（10分）定义在(－1,1)上的奇函数f (x )是减函数，且f (1－a )＋f (1－a 2)<0，求实数a 的取值范围．。

2024-2025学年高一上第一次月考数学试卷（9月份）一、选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的。

1．（5分）已知集合A＝{x∈N|1＜x＜6}，B＝{x|4﹣x＞0}，则A∩B＝（）A．{2，3，4}B．{2，3}C．{2}D．{3}2．（5分）下列说法正确的是（）A．∅∈{0}B．0⊆N C．D．{﹣1}⊆Z3．（5分）命题“∀x∈（0，1），x3＜x2”的否定是（）A．∀x∈（0，1），x3＞x2B．∀x∉（0，1），x3≥x2C．∃x0∈（0，1），D．∃x0∉（0，1），4．（5分）“a＞b”是“a2＞b2”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件5．（5分）若集合A＝{x|2mx﹣3＞0，m∈R}，其中2∈A且1∉A，则实数m的取值范围是（）A．B．C．D．6．（5分）满足集合{1，2}⫋M⊆{1，2，3，4，5}的集合M的个数是（）A．6B．7C．8D．157．（5分）设集合A＝{x|1＜x≤2}，B＝{x|x＜a}，若A⊆B，则实数a的取值范围是（）A．{a|a＜1}B．{a|a≤1}C．{a|a＞2}D．{a|a≥2}8．（5分）已知集合A＝{1，2}，B＝{0，2}，若定义集合运算：A*B＝{z|z＝xy，x∈A，y∈B}，则集合A*B 的所有元素之和为（）A．6B．3C．2D．0二、选择题：本题共3小题，每小题6分，共18分。

在每小题给出的选项中，有多项符合题目要求。

全部选对的得6分，有选错的得0分，部分选对的得部分分。

（多选）9．（6分）已知命题p：x2﹣4x+3＜0，那么命题p成立的一个充分不必要条件是（）A．x≤1B．1＜x＜2C．x≥3D．2＜x＜3（多选）10．（6分）集合A＝{x|ax2﹣x+a＝0}只有一个元素，则实数a的取值可以是（）A．0B．C．1D．（多选）11．（6分）设S是实数集R的一个非空子集，如果对于任意的a，b∈S（a与b可以相等，也可以不相等），都有a+b∈S且a﹣b∈S，则称S是“和谐集”，则下列命题中为真命题的是（）A．存在一个集合S，它既是“和谐集”，又是有限集B．集合{x|x＝3k，k∈Z}是“和谐集”C．若S1，S2都是“和谐集”，则S1∩S2≠∅D．对任意两个不同的“和谐集”S1，S2，总有S1∪S2＝R三、填空题：本题共3小题，每小题5分，共15分。

智才艺州攀枝花市创界学校蒙城县第八二零二零—二零二壹高一数学第一次月考试题〔含解析〕一、选择题〔一共12小题，每一小题5分〕1.设集合A={x∈Q|x＞﹣1}，那么〔〕A. B. C. D.⊈A【答案】B【解析】试题分析：A中元素为大于负一的有理数，应选B．考点：集合间的关系2.集合A到B的映射f：x→y=2x+1，那么集合A中元素2在B中的象是〔〕A.5B.2C.6D.8【答案】A【解析】因为,所以选A.3.用集合表示图中阴影局部是〔〕A.〔∁U A〕∩BB.〔∁U A〕∩〔∁U B〕C.A∩〔∁U B〕D.A∪〔∁U B〕【答案】C............4.以下函数是偶函数的是〔〕A.y=xB.y=2x2﹣3C.D.y=x2，x∈[0，1]【答案】B【解析】y=x为奇函数,y=2x2﹣3是偶函数,为奇函数,y=x2，x∈[0，1]既不是奇函数也不是偶函数,所以选B.5.在以下四组函数中，f〔x〕与g〔x〕表示同一函数的是〔〕A.f〔x〕=x﹣1，g〔x〕=B.f〔x〕=x，g〔x〕=C.f〔x〕=x+1，x∈R，g〔x〕=x+1，x∈ZD.f〔x〕=|x+1|，g〔x〕=【答案】D【解析】f〔x〕=x﹣1与g〔x〕=定义域不同,f〔x〕=x与g〔x〕=定义域不同,f〔x〕=x+1，x∈R 与g〔x〕=x+1，x∈Z定义域不同,g〔x〕=,所以f〔x〕=|x+1|与g〔x〕=为同一函数，选D.6.集合A={0，1，2}，B={z|z=x+y，x∈A，y∈A}，那么B=〔〕A.{0，1，2，3，4}B.{0，1，2}C.{0，2，4}D.{1，2}【答案】A【解析】因为，所以B={0，1，2，3，4}，选A.7.函数f〔x〕=，那么f〔f〔﹣3〕〕=〔〕A.0B.πC.π2D.9【答案】B【解析】，选B.点睛：分段函数求值的解题思路；求分段函数的函数值，要先确定要求值的自变量属于哪一段区间，然后代入该段的解析式求值，当出现f(f(a))的形式时，应从内到外依次求值．8.全集为实数集R，M={x|﹣2≤x≤2}，N={x|x＜1}，那么〔∁R M〕∩N=〔〕A.{x|x＜﹣2}B.{x|﹣2＜x＜1}C.{x|x＜1}D.{x|﹣2≤x＜1}【答案】A【解析】〔∁R M〕∩N={x|x＜﹣2}，选A.9.函数f〔x〕=x2+2ax+a2﹣2a在区间〔﹣∞，3]上单调递减，那么实数a的取值范围是〔〕A.〔﹣∞，3]B.[﹣3，+∞〕C.〔﹣∞，-3]D.[3，+∞〕【答案】C【解析】由题意得，选C.10.函数f〔x〕的定义域为〔﹣1，0〕，那么函数f〔2x+1〕的定义域为〔〕A.〔﹣1，1〕B.〔，1〕C.〔﹣1，0〕D.〔﹣1，﹣〕【答案】D【解析】由题意得，选D.点睛：对于抽象函数定义域的求解(2)假设函数f(g(x))的定义域为[a，b]，那么f(x)的定义域为g(x)在x∈[a，b]上的值域．11.函数y=f〔x〕在定义域〔﹣1，1〕上是减函数，且f〔2a﹣1〕＜f〔1﹣a〕，那么实数a的取值范围是〔〕A. B.〔0，2〕C. D.〔0，+∞〕【答案】C【解析】解：函数y=f〔x〕在定义域〔﹣1，1〕上是减函数，那么有：，应选C．点睛：解函数不等式：首先根据函数的性质把不等式转化为的形式，然后根据函数的单调性去掉“〞，转化为详细的不等式(组)，此时要注意与的取值应在外层函数的定义域内12.设奇函数f〔x〕在〔0，+∞〕上为增函数，且f〔1〕=0，那么不等式＜0的解集为〔〕A.〔﹣1，0〕∪〔1，+∞〕B.〔﹣∞，﹣1〕∪〔0，1〕C.〔﹣∞，﹣1〕∪〔1，+∞〕D.〔﹣1，0〕∪〔0，1〕【答案】D【解析】略二．填空题〔一共4小题，每一小题5分〕13.集合A={1，2，3，4}，集合B={3，4，5}，那么A∩B=_____．【答案】{3，4}．【解析】A∩B={1，2，3，4}∩{3，4，5}={3，4}．14.幂函数f〔x〕=xα的图象经过点〔2，4〕，那么f〔﹣3〕的值是_____．【答案】9．【解析】由题意得15.函数f〔x〕=的单调递减区间为_____．【答案】〔﹣∞，﹣3]．【解析】由题意得，即单调递减区间为〔﹣∞，﹣3]．点睛：1．复合函数单调性的规那么假设两个简单函数的单调性一样，那么它们的复合函数为增函数；假设两个简单函数的单调性相反，那么它们的复合函数为减函数．即“同增异减〞．2．函数单调性的性质(1)假设f(x)，g(x)均为区间A上的增(减)函数，那么f(x)＋g(x)也是区间A上的增(减)函数，更进一步，即增＋增＝增，增－减＝增，减＋减＝减，减－增＝减；(2)假设k>0，那么kf(x)与f(x)单调性一样；假设k<0，那么kf(x)与f(x)单调性相反；(3)在公一共定义域内，函数y＝f(x)(f(x)≠0)与y＝－f(x)，y＝单调性相反；(4)在公一共定义域内，函数y＝f(x)(f(x)≥0)与y＝单调性一样；(5)奇函数在其关于原点对称的区间上单调性一样，偶函数在其关于原点对称的区间上单调性相反．16.函数f〔x〕满足f〔x+y〕=f〔x〕+f〔y〕〔x，y∈R〕，那么以下各式恒成立的是_____．①f〔0〕=0；②f〔3〕=3f〔1〕；③f〔〕=f〔1〕；④f〔﹣x〕f〔x〕＜0．【答案】①②③【解析】解：令x=y=0得f〔0〕=2f〔0〕，所以f〔0〕=0，所以①恒成立；令x=2，y=1得f〔3〕=f〔2〕+f〔1〕=f〔1〕+f〔1〕+f〔1〕=3f〔1〕，所以②恒成立；令x=y=得f〔1〕=2f〔〕，所以f〔〕=f〔1〕，所以③恒成立；令y=﹣x得f〔0〕=f〔x〕+f〔﹣x〕，即f〔﹣x〕=﹣f〔x〕，所以f〔﹣x〕f〔x〕=﹣[f〔x〕]2≤0，所以④不恒成立．故答案为：①②③三．解答题〔一共6小题〕17.集合M={2，a，b}，N={2a，2，b2}且M=N．求a、b的值．【答案】【解析】因为M=N，所以根据集合元素的互异性，可知,解出a,b值再验证是否满足互异性的要求.由M＝N及集合元素的互异性得：或者解上面的方程组得，或者或者再根据集合中元素的互异性得，或者18.集合A={x|1＜x﹣1≤4}，B={x|x＜a}．〔Ⅰ〕当a=3时，求A∩B；〔Ⅱ〕假设A⊆B，务实数a的取值范围．【答案】〔1〕{x|2＜x＜3}〔2〕a＞5【解析】试题分析：〔1〕先解集合A,再结合数轴求交集得A∩B；〔2〕根据数轴确定满足A⊆B时实数a的取值范围．试题解析：解：〔Ⅰ〕∵1＜x﹣1≤4，∴2＜x≤5故A={x|2＜x≤5}当a=3时，B={x|x＜3}∴A∩B={x|2＜x＜3}〔Ⅱ〕∵A⊆B，∴a＞519.f〔x〕=，g〔x〕=x2+2．〔1〕求f〔2〕，g〔2〕，f[g〔2〕]；〔2〕求f[g〔x〕]的解析式．【答案】〔1〕〔2〕【解析】试题分析：〔1〕将自变量2代入f〔x〕，g〔x〕解析式即得f〔2〕，g〔2〕，将g〔2〕作为自变量代入f〔x〕即得f[g〔2〕]；〔2〕将g〔x〕作为自变量代入f〔x〕即得f[g〔x〕]试题解析：解：〔1〕f〔2〕=，g〔2〕=22+2=6，把g〔2〕=22+2=6代入f〔x〕=，得f[g〔2〕]=f〔6〕=；〔2〕f[g〔x〕]=20.函数，〔Ⅰ〕证明f〔x〕在[1，+∞〕上是增函数；〔Ⅱ〕求f〔x〕在[1，4]上的最大值及最小值．【答案】〔1〕见解析〔2〕【解析】试题分析：(Ⅰ)利用函数的单调性的定义进展证明；(Ⅱ)利用前一步所证的函数的单调性确定其最值．试题解析：(Ⅰ)设，且,那么∴∴，∴∴∴，即∴在上是增函数.(Ⅱ)由(Ⅰ)可知在上是增函数∴当时，∴当时，综上所述，在上的最大值为，最小值为.21.设f〔x〕=x2﹣4x﹣4，x∈[t，t+1]〔t∈R〕，求函数f〔x〕的最小值的解析式，并作出此解析式的图象．【答案】见解析【解析】试题分析：根据对称轴x=2与定义区间[t，t+1]位置关系，讨论确定最小值取法，再利用分段函数形式写最小值的解析式，最后按三段依次作出函数图像试题解析：解：f〔x〕=x2﹣4x﹣4=〔x﹣2〕2﹣8，即抛物线开口向上，对称轴为x=2，最小值为﹣8，过点〔0，﹣4〕，结合二次函数的图象可知：当t+1＜2，即t＜1时，f〔x〕=x2﹣4x﹣4，x∈[t，t+1]〔t∈R〕在x=t+1处取最小值f〔t+1〕=t2﹣2t﹣7，当，即1≤t≤2时，f〔x〕=x2﹣4x﹣4，x∈[t，t+1]〔t∈R〕在x=2处取最小值﹣8，当t＞2时，f〔x〕=x2﹣4x﹣4，x∈[t，t+1]〔t∈R〕在x=t处取最小值f〔t〕=t2﹣4t﹣4，即最小值为g〔t〕，由以上分析可得，，作图象如下；点睛：研究二次函数单调性的思路(1)二次函数的单调性在其图象对称轴的两侧不同，因此研究二次函数的单调性时要根据其图象的对称轴进展分类讨论．(2)假设f(x)＝ax2＋bx＋c(a>0)在区间A上单调递减(单调递增)，那么A⊆〔A⊆〕即区间A一定在函数对称轴的左侧(右侧)．22.定义在〔0，+∞〕上的函数f〔x〕满足对任意a，b∈〔0，+∞〕都有f〔ab〕=f〔a〕+f〔b〕，且当x＞1时，f〔x〕＜0．〔Ⅰ〕求f〔1〕的值；〔Ⅱ〕判断f〔x〕的单调性并证明；〔Ⅲ〕假设f〔3〕=﹣1，解不等式f〔x〕+f〔x﹣8〕＞﹣2．【答案】〔1〕f〔1〕=0〔2〕见解析〔3〕〔8，9〕【解析】试题分析：〔1〕赋值法求f〔1〕的值：令a=b=1，可得f〔1〕=2f〔1〕，解得f〔1〕=0；〔2〕取两个特殊值判断函数单调性，再利用单调性定义证明，作差时利用f〔x2〕﹣f〔x1〕=f〔〕再结合当x＞1时，f〔x〕＜0可得差的符号.〔3〕利用及时定义可得f〔x〕+f〔x﹣8〕=f[x〔x﹣8〕]，根据赋值法可得f〔9〕=2f〔3〕=﹣2，再根据单调性可得，解不等式组可得不等式解集试题解析：解：〔1〕对∀a，b∈〔0，+∞〕都有f〔ab〕=f〔a〕+f〔b〕，令a=b=1，可得f〔1〕=2f 〔1〕，解得f〔1〕=0；〔Ⅱ〕证明：设x1，x2∈〔0，+∞〕，且x1＜x2，那么f〔x2〕﹣f〔x1〕=f〔〕﹣f〔x1〕=f〔〕+f〔x1〕﹣f〔x1〕=〕=f〔〕∵，∴，∴f〔x2〕﹣f〔x1〕＜0，即f〔x2〕＜f〔x1〕．∴f〔x〕在〔0，+∞〕上是减函数．〔Ⅲ〕令a=b=3，可得f〔9〕=2f〔3〕=﹣2，∴f〔x〕+f〔x﹣8〕＞﹣2⇒f[x〔x﹣8〕]＞f〔9〕⇒．不等式f〔x〕+f〔x﹣8〕＞﹣2的解集为：〔8，9〕。

高一上学期第一次月考数学试题(含答案解析)学校:___________姓名：___________班级：___________考号：___________第I卷（选择题）一、单选题（本大题共14小题，共56.0分。

在每小题列出的选项中，选出符合题目的一项）1. 设集合A={1,2,3,4}，B={−1,0,2,3}，C={x∈R|−1≤x<2}，则(A∪B)∩C=( )A. {−1,1}B. {0,1}C. {−1,0,1}D. {2,3,4}2. 命题“∀x∈R，x2−2x+1≥0”的否定是( )A. ∃x∈R，x2−2x+1≤0B. ∃X∈R，x2−2x+1≥0C. ∃x∈R，x2−2x+1<0D. ∀x∈R，x2−2x+1<03. 已知集合A={x|−1≤x<4,x∈Z)，则集合A中元素的个数为( )A. 3B. 4C. 5D. 64. 已知集合A={x||x|≥2}，B={x|x2−3x>0}，则A∩B=( )A. ⌀B. {x|x>3，或x≤−2}C. {x|x>3，或x<0}D. {x|x>3，或x≤2}5. 已知p：sinα=√33，q：cos2α=13，则p是q的( )A. 充分不必要条件B. 必要不充分条件C. 充分条件D. 既不充分也不必要条件6. 若M⊆U，N⊆U，且M⊆N，则( )A. M∩N=NB. M∪N=MC. ∁U N⊆∁U MD. ∁U M⊆∁U N7. 已知集合A={x|x<1}，B={x|0≤x≤2}，则A∩B=( )A. {x|0≤x<1}B. {x|1<x≤2}C. {x|x<1}D. {x|x≤2}8. 设b>a>0，c∈R，则下列不等式中不一定成立的是( )A. a12<b12B. 1a −c>1b−c C. a+2b+2>abD. ac2<bc29. 满足关系{1,2}⊆A⊆{1,2,3,4,5}的集合的个数是( )A. 4B. 6C. 8D. 910. 若关于x的不等式ax2+bx−1>0的解集是{x|1<x<2}，则不等式bx2+ax−1<0的解集是( )A. {x|−1<x<23} B. {x|x<−1或x>23}C. {x|−23<x<1} D. {x|x<−23或x>1}11. 已知集合A={x|x2+x−6=0}，B={x|mx+1=0}，且B⊆A，则实数m=( )A. {0,12,−13} B. {−12,13} C. {12,−13} D. {0,−12,13}12. 使不等式1+1x>0成立的一个充分不必要条件是( )A. x>0B. x>−1C. x<−1或x>0D. −1<x<013. 已知命题“∃x∈R，4x2+(a−2)x+14<0”是假命题，则实数a的取值范围是( )A. (−∞,0)B. [0,4]C. [4,+∞)D. (0,4)14. 已知a，b∈R，a2+b2=15−ab，则ab最大值是( )A. 15B. 12C. 5D. 3第II卷（非选择题）二、填空题（本大题共6小题，共24.0分）15. 已知a∈R，b∈R，若集合{a,ba,1}={a2,a−b,0}，则“a2017+b2018”的值为______．16. 当x<−1时，f(x)=x+1x+1的最大值为______．17. 已知集合A={0,1,2}，则集合A的子集共有______个．18. 已知集合A={x|−1<x<2}，B={x|−1<x<m+1}，若x∈A是x∈B成立的一个充分不必要条件，则实数m的取值范围是______．19. 已知{x|ax2−ax+1<0}=⌀，则实数a的取值范围为．20. 已知正数x，y满足x+y=5，则1x+1+1y+2的最小值为______．三、解答题（本大题共4小题，共40.0分。