第二章最小二乘法OLS和线性回归模型知识分享
- 格式:ppt
- 大小:651.50 KB
- 文档页数:90



最小二乘法与线性回归模型线性回归是一种常用的统计分析方法,用于研究因变量与一个或多个自变量之间的关系。
在线性回归中,我们经常使用最小二乘法来进行参数估计。
本文将介绍最小二乘法和线性回归模型,并探讨它们之间的关系和应用。
一、什么是最小二乘法最小二乘法是一种数学优化技术,旨在寻找一条直线(或者更一般地,一个函数),使得该直线与一组数据点之间的误差平方和最小化。
简而言之,最小二乘法通过最小化误差的平方和来拟合数据。
二、线性回归模型在线性回归模型中,我们假设因变量Y与自变量X之间存在线性关系,即Y ≈ βX + ε,其中Y表示因变量,X表示自变量,β表示回归系数,ε表示误差。
线性回归模型可以用来解决预测和关联分析问题。
三、最小二乘法的原理最小二乘法的基本原理是找到一条直线,使得该直线与数据点之间的误差平方和最小。
具体而言,在线性回归中,我们通过最小化残差平方和来估计回归系数β。
残差是观测值与估计值之间的差异。
在最小二乘法中,我们使用一组观测数据(x₁, y₁), (x₂, y₂), ..., (xₙ, yₙ),其中x表示自变量,y表示因变量。
我们要找到回归系数β₀和β₁,使得残差平方和最小化。
残差平方和的表达式如下:RSS = Σ(yᵢ - (β₀ + β₁xᵢ))²最小二乘法的目标是最小化RSS,可通过求导数等方法得到最优解。
四、使用最小二乘法进行线性回归分析使用最小二乘法进行线性回归分析的一般步骤如下:1. 收集数据:获取自变量和因变量的一组数据。
2. 建立模型:确定线性回归模型的形式。
3. 参数估计:使用最小二乘法估计回归系数。
4. 模型评估:分析回归模型的拟合优度、参数的显著性等。
5. 利用模型:使用回归模型进行预测和推断。
五、最小二乘法与线性回归模型的应用最小二乘法和线性回归模型在多个领域都有广泛的应用。
1. 经济学:通过线性回归模型和最小二乘法,经济学家可以研究经济指标之间的关系,如GDP与失业率、通胀率之间的关系。






多元线性回归与最小二乘估计1.假定条件、最小二乘估计量和高斯—马尔可夫定理 多元线性回归模型:y t = β0 +β1x t 1 +β2x t 2 +…+βk - 1x t k -1 + u t(1.1)其中y t 是被解释变量(因变量),x t j 是解释变量(自变量),u t 是随机误差项,βi , i = 0, 1, … , k - 1是回归参数(通常未知)。
对经济问题的实际意义:y t 与x t j 存在线性关系,x t j , j = 0, 1, … , k - 1, 是y t 的重要解释变量。
u t 代表众多影响y t 变化的微小因素。
使y t 的变化偏离了E( y t ) =多元线性回归与最小二乘估计1.假定条件、最小二乘估计量和高斯—马尔可夫定理 多元线性回归模型:y t = β0 +β1x t 1 +β2x t 2 +…+βk - 1x t k -1 + u t(1.1)其中y t 是被解释变量(因变量),x t j 是解释变量(自变量),u t 是随机误差项,βi , i = 0, 1, … , k - 1是回归参数(通常未知)。
对经济问题的实际意义:y t 与x t j 存在线性关系,x t j , j = 0, 1, … , k - 1, 是y t 的重要解释变量。
u t 代表众多影响y t 变化的微小因素。
使y t 的变化偏离了E( y t ) =β0 +β1x t 1 +β2x t 2 +…+βk - 1x t k -1决定的k 维空间平面。
当给定一个样本(y t , x t 1, x t 2 ,…, x t k -1), t = 1, 2, …, T 时, 上述模型表示为y 1 =β0 +β1x 11 +β2x 12 +…+βk - 1x 1 k -1 + u 1, 经济意义:x t j 是y t 的重要解释变量。
y 2 =β0 +β1x 21 +β2x 22 +…+βk - 1x 2 k -1 + u 2, 代数意义:y t 与x t j 存在线性关系。

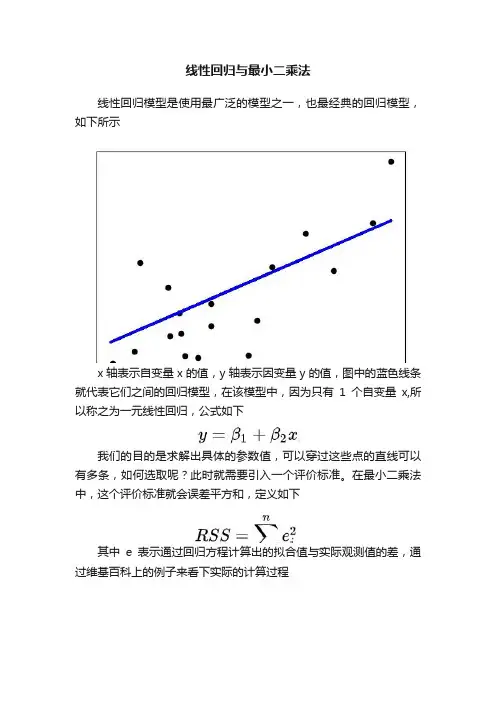
线性回归与最小二乘法线性回归模型是使用最广泛的模型之一,也最经典的回归模型,如下所示x轴表示自变量x的值,y轴表示因变量y的值,图中的蓝色线条就代表它们之间的回归模型,在该模型中,因为只有1个自变量x,所以称之为一元线性回归,公式如下我们的目的是求解出具体的参数值,可以穿过这些点的直线可以有多条,如何选取呢?此时就需要引入一个评价标准。
在最小二乘法中,这个评价标准就会误差平方和,定义如下其中e表示通过回归方程计算出的拟合值与实际观测值的差,通过维基百科上的例子来看下实际的计算过程如上图所示,有4个红色的采样点,在每个点都可以得到(x, y)的观测值,将4个采样点的数据,带入回归方程,可以得到如下结果计算全部点的误差平方和,结果如下对于上述函数,包含了两个自变量,为了求解其最小值,可以借助偏导数来实现。
通过偏导数和函数极值的关系可以知道,在函数的最小值处,偏导数肯定为0,所以可以推导出如下公式对于上述两个方程构成的方程组,简单利用消元法或者代数法就可以快速求出两个参数的值实际上,更加通过的方法是通过矩阵运算来求解,这种方法不仅适合一元线性回归,也适合多元线性回归,其本质是利用矩阵来求解以下方程组计算过程如下>>> data = np.array([[1, 1], [1, 2], [1, 3], [1, 4]])>>> dataarray([[1, 1],[1, 2],[1, 3],[1, 4]])>>> target = np.array([6, 5, 7, 10]).reshape(-1, 1)>>> targetarray([[ 6],[ 5],[ 7],[10]])#先对data矩阵求逆矩阵#再计算两个矩阵的乘积>>> np.matmul(np.matrix(data).I, target)matrix([[3.5],[1.4]])通过一个逆矩阵与矩阵乘积操作,就可以方便的求解参数。
ols最小二乘法OLS最小二乘法是一种常用的线性回归分析方法,它以最小化残差平方和为目标,通过求解最小二乘估计量来拟合回归模型。
这种方法在统计学领域有着广泛的应用,尤其是在经济学、金融学等领域,被广泛应用于关于各种变量之间的关系分析。
在OLS最小二乘法中,首先需要确定一个线性回归方程,假设我们有n个样本数据,其中每个样本都包含p个自变量和一个因变量,可以表示为y = β0 + β1x1 + β2x2 + …… + βpxp + ε,其中β0是截距项,β1~βp是自变量的系数,ε是误差项。
我们的目标是通过OLS方法来估计出β0~βp的值,从而得到回归方程,使其拟合样本数据最佳。
在OLS方法中,我们通过最小化残差平方和来估计回归系数,即通过使得所有样本数据的误差平方和最小来确定回归系数的值。
残差平方和是指所有样本数据的误差的平方和,即∑(y - y_hat)²。
其中y 表示样本数据的实际值,y_hat表示回归模型的预测值。
在确定回归系数的过程中,我们需要通过OLS估计出β0~βp的值,即使得残差平方和最小的β0~βp的值。
这个过程可以通过求解回归方程的正规方程组来实现,即(X'X)β = X'y,其中X是n*p的自变量矩阵,y是n*1的因变量向量,β是p*1的系数向量。
通过求解正规方程组,我们可以得到β的最小二乘估计值。
需要注意的是,OLS方法只能用于线性回归分析,且要求自变量之间不存在多重共线性,即自变量之间不能完全线性相关。
此外,在使用OLS方法时,还需要对回归结果进行显著性检验和模型拟合度检验,以确保回归结果的可靠性。
OLS最小二乘法是一种常用的线性回归分析方法,它通过最小化残差平方和来估计回归系数,从而得到回归方程,使其拟合样本数据最佳。
在使用OLS方法时,需要注意线性回归和多重共线性的问题,并对回归结果进行显著性检验和模型拟合度检验。