框架结构内力计算

框架和剪力墙结构的内力与位移计算在建筑结构设计中，框架和剪力墙结构是一种常见且重要的结构形式。

理解和准确计算这种结构的内力与位移，对于确保建筑物的安全性、稳定性以及使用性能至关重要。

框架结构主要由梁和柱组成，通过节点连接形成空间受力体系。

在承受水平荷载时，框架结构的变形以剪切型为主，即层间位移由下至上逐渐增大。

而剪力墙结构则是由一系列的钢筋混凝土墙板组成，能够有效地抵抗水平荷载，其变形以弯曲型为主，即顶部位移较大。

当框架和剪力墙共同工作时，其内力和位移的计算就变得较为复杂。

首先，我们来探讨内力的计算。

内力包括弯矩、剪力和轴力。

在水平荷载作用下，框架和剪力墙所承担的内力会根据它们的刚度比例进行分配。

对于框架部分，其内力计算通常采用 D 值法。

D 值法考虑了梁柱线刚度比、上下层横梁线刚度比以及层高变化等因素对框架柱抗侧刚度的影响。

通过计算得到框架柱的抗侧刚度后，再根据水平荷载的大小和分布，就可以计算出框架柱和框架梁的内力。

剪力墙的内力计算则相对复杂一些。

一般来说，可以采用等效抗弯刚度法或者连续连杆法。

等效抗弯刚度法将剪力墙等效为一个悬臂梁，通过计算其等效抗弯刚度来确定内力。

连续连杆法则是将剪力墙视为一系列连续的连杆，通过建立微分方程来求解内力。

在计算框架和剪力墙结构的位移时，需要分别考虑弯曲变形和剪切变形的影响。

对于框架结构，由于其剪切变形较大，需要同时考虑梁柱的弯曲变形和剪切变形。

而剪力墙结构主要是弯曲变形，其位移计算可以基于材料力学中的弯曲理论。

在实际工程中，为了更准确地计算框架和剪力墙结构的内力和位移，通常会借助计算机软件进行分析。

这些软件基于有限元法等数值方法，能够模拟结构在各种荷载作用下的响应。

然而，软件计算结果也并非绝对准确，工程师还需要根据自己的经验和判断对结果进行分析和校核。

例如，在一些特殊的情况下，软件可能无法准确考虑结构的非线性行为或者一些复杂的边界条件。

另外，在设计过程中，还需要考虑一些其他因素对内力和位移的影响。

水平荷载作用下框架内力的计算——D值法资料讲解D值法是一种常用于计算框架结构在水平荷载作用下的内力的方法。

下面是对D值法进行详细讲解的资料。

一、D值法的基本概念D值法是一种近似计算框架结构内力的方法，其基本思想是通过估算框架结构在水平荷载作用下的刚度来计算内力。

具体而言，D值法通过假设结构刚度的变化与结构的变形呈线性正比关系，将结构的刚度表示为一个D值，再通过对结构的初始刚度和变形的估计，计算出结构在水平荷载作用下的内力。

二、D值的计算步骤（一）计算结构的初始刚度1.根据结构的几何形状和材料特性，计算出结构在初始状态下的刚度矩阵。

2.对刚度矩阵进行变换，得到初始刚度矩阵。

（二）估算结构的变形1.假设结构受到线性弹性变形的影响。

2.估计结构的位移和转角。

（三）计算D值1.根据估算的位移和转角，计算出结构的变形矩阵。

2.根据初始刚度矩阵和变形矩阵，计算出结构的刚度矩阵。

3.将刚度矩阵转化为D值，即刚度指数。

（四）计算内力1.根据D值和水平荷载的大小，计算出结构的内力。

2.对结构的各个部位进行内力平衡计算，得到各个构件的内力。

三、D值法的优缺点D值法在计算框架结构内力时具有一定的优势和局限性。

（一）优点1.简洁易行：D值法不需要进行繁琐的矩阵计算，计算步骤相对简单。

2.适用范围广：D值法适用于一般的框架结构，包括多层和复杂形状的结构。

3.结果可靠：在合理的假设和估计前提下，D值法可以得到较为准确的内力计算结果。

（二）缺点1.假设过于理想化：D值法假设结构的变形与刚度呈线性正比关系，这在实际情况下不一定成立。

2.忽略非线性效应：D值法无法考虑结构中的非线性效应，如材料的非线性和连接件的滑动、屈曲等。

3.精度受限：由于D值法是一种近似计算方法，其精度相对有限，不适用于对结构内力要求较高的情况。

四、D值法的应用领域D值法在实际工程中被广泛应用，特别是在简化计算和快速评估结构内力的情况下。

1.结构抗震设计：D值法常用于抗震设计中，通过快速计算内力，进行结构的抗震性能评估。

框架结构的内力与位移计算4．1 概述框架结构是目前多、高层建筑中常采用的结构形式之一。

框架在结构力学中称为刚架，结构力学中已经比较详细地介绍了超静定刚架(框架)内力和位移的计算方法，比较常用的手算方法有全框架力矩分配法、无剪力分配法和迭代法等，均为精确算法。

但在实用中大多已被更精确、更省人力的计算机分析方法(矩阵位移法)所代替。

不过，其中有些手算近似计算方法由于其计算简单、易于掌握，又能反映刚架受力和变形的基本特点，目前在实际工程中应用还很多，特别是在初步设计时的估算，手算的近似方法仍为设计人员所常用。

多、高层建筑结构在进行内力与位移计算中，为使计算简化，必须作出一些假定，以下将讨论一些结构计算中的基本假定：(1)弹性工作状态假定：结构在荷载作用下的整体工作按弹性工作状态考虑，内力和位移按弹性方法计算。

但对于框架梁及连梁等构件，可考虑局部塑性变形，内力重分布。

(2)平面结构假定：任何结构都是一个空间结构，实际风荷载及地震作用方向是随意的、不定的。

为简化计算，对规则的框架、框架—剪力墙、剪力墙结构体系及框筒结构，可将结构沿两个正交主轴方向划分为若干平面抗侧力结构—若干榀框架、若干片墙，以承受该框架、墙平面方向的水平力(风荷载及水平地震作用)，框架、墙不承受垂直于其平面方向的水平力。

(3)刚性楼面假定：各平面|考试大|抗侧力结构之间通过楼板相互联系并协同工作。

一般情况下，可认为楼板在自身平面内刚度无限大，而楼板平面外刚度很小，可以不考虑。

为保证楼面在平面内刚度，在设计中应采取相应的构造措施。

但当楼面有大开孔、楼面上有较长的外伸段、底层大空间剪力墙结构的转换层楼面以及楼面的整体性较差时，宜对采用刚性楼面假定的计算结果进行调整或在计算中考虑楼面的平面内刚度。

在上述假定下，内力分析时要解决两个问题：一个是按各片抗侧力结构的相对刚度大小，分配水平荷载至各片抗侧力结构；另一个是计算每片抗侧力结构在所分到的水平荷载作用下的内力及位移。

框架结构在竖向荷载作用下的内力计算
框架结构在竖向荷载作用下的内力计算可近似地采用分层法.
在进行竖向荷载作用下的内力分析时,可假定：（1）作用在某一层框架梁上的竖向荷载对其他楼层的框架梁的影响不计,而仅在本楼层的框架梁以及与本层框架梁相连的框架柱产生弯矩和剪力.（2）在竖向荷载作用下,不考虑框架的侧移.
计算过程可如下：
（1）分层：分层框架柱子的上下端均假定为固定端支承,
（2）计算各个独立刚架单元：用弯矩分配法或迭代法进行计算各个独立刚架单元.而分层计算所得的各层梁的内力,即为原框架结构中相应层次的梁的内力.
（3）叠加：在求得各独立刚架中的结构内力以后,则可将相邻两个独立刚架中同层同柱号的柱内力叠加,作为原框架结构中柱的内力.
叠加后为原框架的近似弯距图,由于框架柱节点处的弯矩为柱上下两层之和因此叠加后的弯距图,在框架节点处常常不平衡.这是由于分层计算单元与实际结构不符所带来的误差.若欲提高精度,可对节点,特别是边节点不平衡弯矩再作一次分配,予以修正.。

框架结构竖向荷载作用下的内力计算框架结构是由梁柱等构件组成的，在受到竖向荷载作用下，会引起构件内力的产生。

了解框架结构竖向荷载作用下的内力计算对于结构的设计和分析非常重要。

下面将详细介绍框架结构竖向荷载作用下的内力计算方法。

首先，通过建立结构模型来描述框架结构。

结构模型中包括构件、节点和连接关系。

构件可以是梁或柱，节点是构件之间的连接点，连接关系表示构件之间的刚性约束。

在竖向荷载作用下，框架结构的内力主要有两种情况：梁内力和柱内力。

1.梁内力计算：在竖向荷载作用下，梁会产生弯矩和剪力。

根据梁的基本理论，可以得出计算弯矩和剪力的公式。

-弯矩计算：弯矩是由竖向荷载作用在梁上引起的。

根据弯矩的定义，弯矩M等于施加在梁上的力乘以力臂。

当梁需要承受重力荷载时，弯矩的计算公式为M=w*l^2/8，其中w为荷载大小，l为梁的跨度。

-剪力计算：剪力是由竖向荷载作用在梁上引起的。

根据剪力的定义，剪力V等于施加在梁上的力。

当梁需要承受重力荷载时，剪力的计算公式为V=w*l/2，其中w为荷载大小，l为梁的跨度。

2.柱内力计算：在竖向荷载作用下，柱会产生压力和拉力。

根据柱的基本理论，可以得出计算压力和拉力的公式。

-压力计算：压力是由竖向荷载作用在柱上引起的。

根据力学平衡原理，压力P等于施加在柱上的荷载之和。

当柱需要承受多个重力荷载时，压力的计算公式为P=∑w，其中w为荷载大小。

-拉力计算：拉力是由竖向荷载作用在柱上引起的。

和压力类似，拉力T等于施加在柱上的荷载之和。

在实际计算过程中，需要考虑梁和柱的截面形状和材料性质，以及节点和连接部位的刚性约束等因素。

同时，还需要考虑结构的整体平衡条件和节点处的力的平衡条件。

在计算过程中，可以使用静力平衡原理和弹性力学理论来进行分析。

通过平衡方程和应变-位移关系等基本原理，可以建立结构方程组，并通过求解方程组得到内力的值。

总结起来，框架结构竖向荷载作用下的内力计算是一个复杂的过程，需要考虑多个因素和使用多种方法。

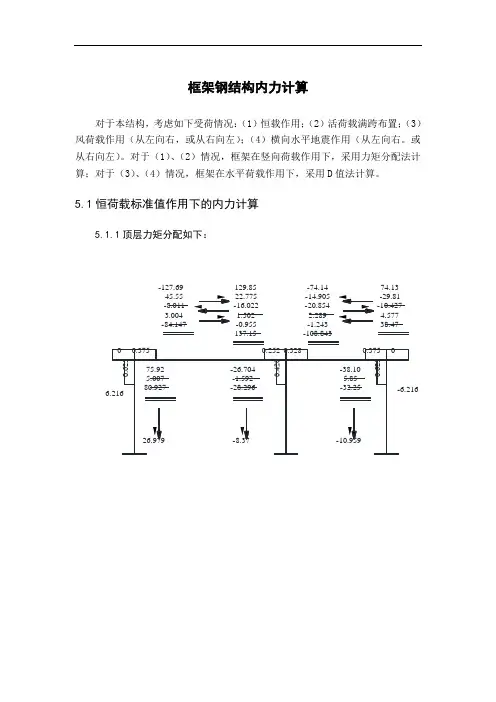
框架钢结构内力计算对于本结构，考虑如下受荷情况：（1）恒载作用；（2）活荷载满跨布置；（3）风荷载作用（从左向右，或从右向左）；（4）横向水平地震作用（从左向右。

或从右向左）。

对于（1）、（2）情况，框架在竖向荷载作用下，采用力矩分配法计算；对于（3）、（4）情况，框架在水平荷载作用下，采用D值法计算。

5.1恒荷载标准值作用下的内力计算5.1.1顶层力矩分配如下：-127.6945.55-8.0113.004-84.147129.8522.775-16.0221.502-0.955137.1574.13-29.81-10.4274.57738.47-74.14-14.905-20.8542.289-1.243-108.843顶层-10.544-8.757三层5.1.3二层力矩分配如下：-11.212-9.203二层0.174.50.185.48.4760.1420.21500.326.265.39-193.8428.684-7.4521.297-171.311214.6814.342-14.9050.649-0.240214.526114.81-18.451-9.7092.08788.737-114.81-9.226-19.4181.044-0.313-142.72382.4253.72686.15142.455-27.815-0.449-28.264-26.5183.00-23.518底层-42.825-0.691-43.516-21.758-40.854.62-36.23-18.11453.7412.42955.85818.724-9.422-7.83928.99-28.99叠加可得到最终的梁端、柱端弯矩。

其次求各层梁的最大弯矩，由于各层梁的最大弯矩求法相同，故此处列举顶层梁AC做实例。

由力矩分配法已求得：第一个集中力处剪力同理在顶梁AC段，第二个集中荷载处，剪力变号，故此处弯矩最大。

同理可求得其它梁的最大弯矩及梁端剪力，列表如下：梁剪力表层号 4 3 2 1 AC跨69.98 117.48 114.67 115.3566.95 101.83 100.62 101.3019.35 38.39 37.18 37.86 16.45 23.45 23.77 24.45 -32.15 -39.99 -39.67 -38.99 -34.19 -55.64 -53.72 -53.04 -81.79 -119.08 -117.16 -116.48 -84.55 -133.30 -129.93 -129.25CD跨62.91 96.97 93.99 92.50 59.88 81.32 79.94 78.45 12.28 17.88 16.50 15.01 9.38 2.94 3.10 1.61 -38.22 -60.50 -60.34 -61.83 -41.26 -76.15 -74.39 -75.88（注：表中单位为kN）梁跨最大弯矩，柱轴力计算如下表：层号4 上146.14 220.49 117.42101.05 48.96 下154.23 228.57 125.503 上401.64 536.69 331.59137.85 65.51 下408.84 543.90 338.212 上647.40 843.20 537.07134.70 64.06 下654.60 850.40 544.271 上893.84 1147.53 744.036132.41 62.77 下907.62 1161.31 757.82柱的剪力可根据平衡方程求出。

框架结构内力计算内力是中国武术文化的重要组成部分，是武术修炼的核心。

在武术理论中，内力被认为是一种身体内部潜在能量，可以通过特定的修炼方法进行培养和运用。

内力计算的框架结构通常包括内力的定义、培养方法和运用技巧。

首先，内力的定义是理解内力计算的基础。

内力是指通过特定的方法和技巧，通过身体内部的调养和培养，将自身的精气神凝聚到一定程度，形成一种具有弹性和力量的能量。

内力的培养过程主要包括呼吸调节、意念导引和体能锻炼等。

其次，内力的培养方法是实现内力计算的重要环节。

内力培养的方法多种多样，但核心思想是通过特定的运动和呼吸方法调整身体内部的能量流动，从而激发和培养内力。

具体的培养方法包括：深呼吸法、气功练习、站桩功、助力发散法等。

这些方法通过疏通经络、调和气血、提升肢体协调性等途径，不断促进内力的积累和壮大。

最后，内力的运用技巧是内力计算的关键环节。

拥有丰富内力的武者可以通过各种技巧将内力用于实际战斗中。

内力的运用技巧主要包括：气劲输出、内力释放和内力应用等。

气劲输出指的是将内力输送至特定部位，如拳头、掌心等，从而提升攻击力和防御力。

内力释放指的是将内力通过特定的动作和姿势释放出来，产生震惊力和冲击力。

内力应用则是将内力融入到各种招式和技法中，实现技击的准确和威力性。

综上所述，内力计算的框架结构主要包括内力的定义、培养方法和运用技巧。

在武术修炼中，内力的培养和运用是实现武者身体和意识力量统一的重要手段。

通过不断的修炼和实践，武者可以掌握内力的计算技巧，提升武术实力。

竖向荷载作用下框架结构的内力计算6.1计算单元的选择确定取③轴线横向框架进行计算，如下图所示：图6.1框架计算简图计算单元宽度为6.4 m，由于房间内布置有次梁，故直接传给该框架的楼面荷载如图中的水平阴影所示。

计算单元范围内的其余楼面荷载则通过次梁和纵向框架梁以集中力的形式传给横向框架，作用于各节点上。

由于纵向框架梁的中心线与柱的中心线不重合，所以在框架节点上还作用有集中力矩。

6.2荷载计算6.2.1恒载作用下柱的内力计算：恒荷载作用下各层框架梁上的荷载分布如下图所示：2图6.2恒荷载作用下各层框架梁上的荷载分布图（1）、对于顶层屋面，q1、q1＇代表横梁自重，为均布荷载形式。

q1=0.3×0.75×25=5.625kN/mq1＇=0.3×0.75×25=5.625kN/mq2为屋面板传给横梁的梯形荷载。

q2=5.29×3.2=16.928kN/mP1、P2分别由边纵梁、中纵梁直接传给柱的恒载，它包括主梁自重、次梁自重、楼板重等重力荷载，计算如下：P1=6.4*0.3*0.75*25+8.5/2*0.25*0.6*25+5.29*3.2*1.6+(5.3+8.5)*1.6*5.29/4=108.223KN P2=6.4*0.3*0.75*25+6.4/2*0.25*0.6*25+5.29*3.2*1.6 +(3.2+6.4)*1.6*5.29/4=95.398KN P3=6.4*0.3*0.75*25+(8.5+6.4)*0.5*0.25*0.6*25+5.29*3.2*1.6*2++(3.2+6.4)*1.6*5.29/4= 190.64KN集中力矩M1=P1e1=108.223×（0.6 -0.3）/2=16.23kN·mM2=P2e2=147.23×（0.6 -0.3）/2=14.31kN·m（2）、对于3层，包括梁自重和其上横墙自重，为均布荷载，其它荷载的计算方法同第顶层。

§13.3 框架结构的内力与位移计算一、竖向荷载作用下的内力近似计算方法——— 分层法1. 基本假定（1） 在竖向荷载作用下，多层多跨框架的侧移很小可忽略不计。

（2） 每层梁上的荷载只对本层的梁和上、下柱产生内力对其他各层梁及其他柱内力的影响可忽略不计。

2. 计算方法（1）将多层框架分层，以每层梁与上下柱组成的单层框架作为计算单元，柱远端假定为固端。

（2）用力矩分配法分别计算每个计算单元的内力。

（3）在分层计算时，假定上、下柱的远端是固定的，但实际上有转角产生，是弹性支承。

为消除由此所带来的误差，可令除底层柱外，其他每层柱的线刚度均乘以0.9的折减系数（底层铰结时为0.75） ，相应的弯矩传递系数取1/3，底层柱弯矩传递系数仍为1/2。

（4）分层计算所得的梁端弯矩即为最后弯矩，而每根柱分别属于上下两个计算单元，所以柱端弯矩要进行叠加。

叠加后节点上的弯矩可能不平衡，但一般误差不大，若欲进一步修正则可对节点的不平衡弯矩作一次弯矩分配，但不再传递。

二、水平荷载作用下的内力近似计算方法 （一） ——反弯点法对在水平荷载作用下的框架内力近似计算，一是需要确定各柱间的剪力分配比；二是要确定各柱的反弯点位置。

1.基本假定（1）梁的线刚度无限大，各柱上下两端只有水平位移没有角位移，且同一层柱中各端的水平位移相等。

（2）框架底层柱的反弯点在距柱底2/3柱高处，其余各层柱的反弯点在柱高的中点。

（3）梁端弯矩可由节点平衡条件求出。

2.计算方法（1）同层各柱剪力的确定首先求出同层每根框架柱的抗侧移刚度d = 12i c / h 2 ，式中i c = EI/ h 称为柱的线刚度，h 为层高。

柱的抗侧移刚度d 表示柱端产生单位水平位移Δu = 1时，在柱端所需施加的水平力大小。

设框架结构共有n 层，每层共有j 根柱子，则第i 层各柱在反弯点处剪力计算式为：i j j ji ji V dd ∑==1 Vij 式中 V ij ———第i 层第j 根柱子的剪力；d ij ———第i 层第j 根柱子的侧移刚度；∑d ij ———第i 层j 根柱子的侧移刚度总和；Vi ———第i 层楼层总剪力，为第i 层及第i 层以上所有水平荷载总和。

第8章 一榀框架计算8.7框架内力计算框架结构承受的荷载主要有恒载、活载、风荷载、地震作用。

其中恒载、活载为竖向荷载,风荷载和地震为水平作用。

手算多层多跨框架结构的内力和侧移时，采用近似方法。

求竖向荷载作用下的内力采用分层法，求水平荷载作用下的内力采用反弯点法、D 值法。

在计算各项荷载作用下的效应时,一般按标准值进行计算，然后进行荷载效应组合。

8.7.2框架内力计算1。

恒载作用下的框架内力 (1）计算简图将图8-12（a ）中梁上梯形荷载折算为均布荷载。

其中a=1。

8m ，l=6.9m ，=1800/69000.26a α==,顶层梯形荷载折算为均布荷载值:232312+=120.26+0.2621.31=18.8kN m q αα-⨯-⨯⨯（）（），顶层总均布荷载为18.8+4.74=23.54kN m 。

其他层计算方法同顶层，计算值为21.63kN m 。

中间跨只作用有均布荷载,不需折算。

由于该框架为对称结构,取框架的一半进行简化计算,计算简图见8-19。

（2）弯矩分配系数节点A 1:101044 1.18 4.72A A A A S i ==⨯=111144 1.33 5.32A B A B S i ==⨯=12120.940.94 1.61 5.796A A A A S i =⨯=⨯⨯=()0.622 1.3330.84415.836AS =++=∑1010 4.720.29815.836A A A A AS S μ===∑图8-19 恒载作用下计算简图（括号内数值为梁柱相对线刚度）1111 5.320.33615.836A B A B AS S μ===∑1212 5.7960.36615.836A A A A AS S μ===∑ 节点B 1:11112 1.12 2.24B D B D S i ==⨯=18.076BS =∑1111 5.320.29418.076B A B A BS S μ===∑1010 4.720.32118.076B B B B BS S μ===∑ 1212 5.7960.32118.076B B B B BS S μ===∑1111 2.240.12418.076B D B D BS S μ===∑节点A 2:()210.94 1.610.4170.94 1.610.776 1.33A A μ⨯⨯==⨯⨯++230.940.7760.20113.91A A μ⨯⨯==224 1.330.38213.91A B μ⨯==节点B 2:224 1.330.3294 1.330.94 1.61+0.940.7762 1.12B A μ⨯==⨯+⨯⨯⨯⨯+⨯210.94 1.610.35916.15B B μ⨯⨯==212 1.120.13916.15B C μ⨯==230.940.7760.17316.15B B μ⨯⨯==节点A 3 、A 4、A 5与A 2相同B 3、B 4、B 5与B 2相同。