范德华方程计算容器内气体的压力
- 格式:ppt
- 大小:215.50 KB
- 文档页数:4

范德华方程常数范德华方程常数是描述非理想气体行为的重要参数之一。
它是根据实验数据拟合得到的,可以用来衡量气体分子间的相互作用程度。
范德华方程常数包括范德华吸引常数(a)和范德华斥力常数(b),它们对应了气体分子间的吸引力和斥力。
范德华方程常数的引入是为了修正理想气体方程,使其更加适用于实际气体的行为。
理想气体方程假设气体分子之间没有相互作用,而实际气体分子之间存在吸引力和斥力,因此需要引入修正项。
范德华方程可以写为:P = (nRT)/(V - nb) - a(n/V)^2其中,P表示气体的压强,n表示气体的物质的量,R表示气体常数,T表示气体的温度,V表示气体的体积。
范德华方程常数a和b可以根据实验数据进行拟合得到。
范德华吸引常数a表示气体分子之间的吸引力,它的值越大,吸引力越强。
范德华斥力常数b表示气体分子之间的斥力,它的值越大,斥力越强。
范德华方程常数的值与气体的性质有关。
不同气体的分子间相互作用不同,因此它们的范德华方程常数也不同。
例如,极性分子之间的相互作用较强,其范德华方程常数的值较大;而非极性分子之间的相互作用较弱,其范德华方程常数的值较小。
范德华方程常数的应用非常广泛。
在化学工程领域,它常被用来描述气体的物理性质,如压力、密度、温度等。
在化学反应工程中,范德华方程常数的值可以用来预测气体的行为,从而优化反应条件和改进工艺。
范德华方程常数还可以用来计算气体的偏差因子(压缩因子),从而更准确地描述气体的行为。
偏差因子是实际气体与理想气体之间的差异,它的值与范德华方程常数密切相关。
范德华方程常数是描述气体分子间相互作用的重要参数。
通过引入范德华方程常数,可以修正理想气体方程,使其更适用于实际气体的行为。
范德华方程常数的值与气体的性质有关,不同气体的范德华方程常数不同。
范德华方程常数在化学工程和化学反应工程中有着广泛的应用,可以用来描述气体的物理性质,预测气体的行为,以及计算偏差因子等。

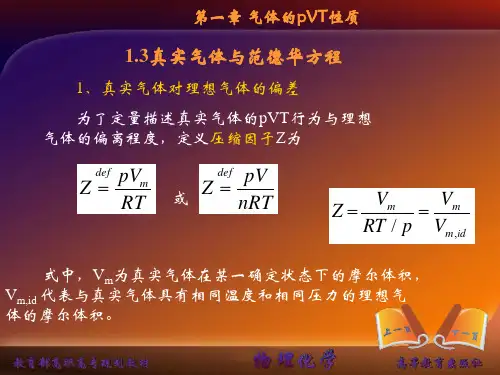
2van der Waals 状态方程及其对科学的贡献19世纪初,在Boyle(玻义耳)、Gay -Lussac(盖-吕萨克)和Avogadro(阿伏伽德罗)等学者的努力下,一个能够描述低密度气体pVT 行为的经验方程pV m =RT (2-1)已被确立,式中R 是一个普适的常数,称为摩尔气体常数,V m 为气体的摩尔体积。
但是,要说发展成一个理论,应当归功于德国物理学家R J E Clausius(克劳修斯),他在1857年首先用气体分子运动论导得了这个方程。
在推导中,他为低密度气体设想了如下微观模型:①气体是大量分子的集合体。
②分子在容器中作无规则运动,它们的运动遵守牛顿运动定律。
③分子本身的大小可以忽略不计。
④除了碰撞外,分子间没有相互作用。
⑤分子间和分子与器壁间的碰撞是弹性碰撞。
显而易见,这是一个十分粗放的理想模型。
完全符合这种模型的气体称为理想气体。
故式(2-1)称为理想气体状态方程。
理想气体状态方程的一个显著特征是:它的等温线总是一些双曲线。
无论温度多么低,压力多么高,都不可能使其液化,故理想气体是一种永久气体。
显然,这与人们的经验很不相符。
经验表明,任何物质都能够气液相变,在一定的温度下都有确定的饱和蒸气压,温度愈高,饱和蒸气压愈大。
然而,这种平衡关系是否会随温度的升高而无限地保持下去呢?这个看似简单的问题,却让不少著名物理学家困惑了近50年,直到1869年才得出了明确的结论。
这归功于英国物理学家T Andrews(安德鲁斯),他用了将近十年的时间,对气体的压缩性做了一系列实验,特别是二氧化碳。
他发现随着温度的升高,平衡的气液两相密度差逐渐缩小,到了31℃时,两者差别消失,蒸发焓变为零,即气液平衡到此终止。
Andrews 称此为“临界点”,意即以此为界,当温度超过31℃时,无论压力多高,都不可能使气体液化。
当Andrews 将这些实验结果在英国皇家学会作了题为“论物质液态和气态的连续性”报告后,立即引起了世界各国学者的关注。


气体状态方程及其应用气体是物质的一种常见形态,广泛存在于自然界和工业生产中。
了解气体的状态方程对于理解和应用气体的性质和行为非常重要。
本文将介绍气体的状态方程以及它在科学和工程领域的应用。
一、气体状态方程气体状态方程描述了气体的性质和行为,它是通过实验和理论推导得到的。
目前最常用的气体状态方程有理想气体状态方程和范德华气体状态方程。
理想气体状态方程是最简单和最常用的气体方程,它建立在以下假设基础上:1. 气体分子之间没有相互作用力;2. 气体分子之间体积可忽略不计。
根据这些假设,理想气体状态方程可以表示为:PV = nRT其中,P为气体的压强,V为气体的体积,n为气体的摩尔数,R为气体常量,T为气体的温度。
该方程可以用来计算气体在不同条件下的状态。
另一个常用的气体状态方程是范德华气体状态方程,它考虑了气体分子间的相互作用力对气体性质的影响。
范德华气体状态方程可以表示为:(P + an^2/V^2)(V - nb) = nRT其中,a和b是范德华常数,与气体的性质有关。
该方程在高压和低温条件下更精确地描述了气体的状态。
二、气体状态方程的应用1. 气体的状态计算气体状态方程可以用于计算气体在不同条件下的状态,例如计算气体的压力、体积、温度等。
通过对气体状态方程进行适当的变换和计算,可以得到所需的气体性质数据。
2. 气体混合物的性质分析在实际应用中,往往会遇到多个气体混合在一起的情况。
气体状态方程可以帮助我们分析和计算气体混合物的性质,例如气体的总压力、分压力以及摩尔分数等。
3. 气体反应的计算在化学反应中,气体常常作为反应物或生成物参与其中。
通过气体状态方程,可以计算气体反应的平衡常数、反应速率等重要参数,从而对反应过程进行研究和优化。
4. 气体的密度和摩尔质量计算气体状态方程可以通过变换和计算,得到气体的密度和摩尔质量。
这对于工程设计、分析和实验中的气体计量非常重要,例如在空气污染监测中的应用。
5. 气体的溶解度和扩散率研究气体溶解度和扩散率是气体在液体中的重要性质。



普化无机试卷(气体一)一、选择题1. (0101)较多偏离理想气体行为的气体, 其分子具有----------------------------------------( )(A) 较高的分子速率(B) 较小的相对分子质量(C) 较大的分子体积(D) 较弱的分子间作用力2. (0102)按SI 制气体常数R的取值是------------------------------------------------------------( )(A) 82.06 dm3·atm·K-1·mol-1(B) 8.314 J·K-1·mol-1(C) 1.987 cal·atm·K-1·mol-1(D) 0.082 cal·K-1·mol-13. (0103)现有1 mol 理想气体, 若它的摩尔质量为M,密度为d,在温度T下体积为V,下述关系正确的是----------------------------------------------------------------------------------------( )(A) pV=(M/d)RT(B) pVd = RT(C) pV=(d/n)RT(D) pM/d = RT4. (0104)相同的温度、压力条件下, 1 g 下列各种物质, 占体积最大的是-------------------( ) (相对原子质量:H 1, C 12, O 16, Ne 20, S 32)(A) 乙烷(B) 氖(C) 氧(D) 硫化氢5. (0105)用Meyer 法测定0.15 g 挥发性液体, 在标准温度和压力下, 其体积为20 cm3,该化合物的相对分子质量约为-------------------------------------------------------------------------( )(A) 85 (B) 168 (C) 340 (D) 456. (0106)在T,p 相同下,气体A充满烧瓶时,测得A为0.34 g , 而充满O3时, 测得其为0.48 g , 则气体A是-------------------------------------------------------------------------------------------( )(A) O2(B) SO2(C) H2S (D) 无法判断7. (0108)某气体AB,在高温下建立下列平衡:AB(g) +B(g). 若把1.00 mol 此气体在T= 300 K,p= 101 kPa 下放在某密闭容器中, 加热到600 K时, 有25.0 %解离。

第一次作业中文教材:1-14 氮气在273.2K 时的摩尔体积为70.3×10-6m 3,试计算其压力。
(1)用理想气体状态方程式;(2)用范德华方程式; (3)用压缩因子图法。
将上述结果与实验值比较(实验值为40530kPa ) 解答:(1)据pV nRT = p=68.314273.270.310-⨯⨯Pa=3.23×106Pa (2) N 2的范德华参量据课本34页表1-7查得620.1368..a Pa m mol -= 63138.610.b m mol --=⨯p=2m m RT a V b V --=62128.314273.20.1368(70.338.6)1070.310Pa Pa --⨯--⨯⨯=4.40×107Pa (3) 由课本31页表1-6查得:T c =126.3K p c =3394.4kPa V c,m =90.1×10-3dm 3.mol -1 T r =c T T =273.2 2.165126.3= 压缩因子定义m pV Z RT=p=Z m RT V =3.23×107Z.Pa p r =9.52c pZ p = 在T r =2.165附近,作p r ~Z 直线,此直线交T r 于Z=1.24处,此Z 值即为同时满足T r =2.165和P r =9.52Z 的对应态的压缩因子值,以之代入公式得 P=3.23×107×1.24Pa=40.4MPa1-17 (1)若以下方程式中的a 具有范德华常数a 的量纲,试由量纲分析确定以下两方程式中哪一个属量纲上正确的?哪一个属量纲上不正确的? (a) 1V m p p a T T V RT ⎛⎫∂⎛⎫=+ ⎪⎪∂⎝⎭⎝⎭ (b) 21V m p p a T T V RT ⎛⎫∂⎛⎫=+ ⎪⎪∂⎝⎭⎝⎭(2) 某生于考试中对算术平均速度公式记忆已模糊不清,仿佛是u =其中x 为待定的物理量,试用量纲分析帮助他确定下来。


范德华方程范德华方程范德华方程是范德瓦耳斯方程的另一种翻译,简称范氏方程,是荷兰物理学家范德瓦耳斯(van der Waals,又译“范德华”、“凡德瓦耳”)于1873年提出的一种实际气体状态方程。
1范德华方程范德华方程是范德瓦耳斯方程的另一种翻译,简称范氏方程,是荷兰物理学家范德瓦耳斯(van der Waals,又译“范德华”、“凡德瓦耳”)于1873年提出的一种实际气体状态方程。
范氏方程是对理想气体状态方程的一种改进,特点在于将被理想气体模型所忽略的的气体分子自身大小和分子之间的相互作用力考虑进来,以便更好地描述气体的宏观物理性质。
2适用范围范氏方程对气-液临界温度以上流体性质的描写优于理想气体方程。
对温度稍低于临界温度的液体和低压气体也有较合理的描述。
但是,当描述对象处于状态参量空间(P,V,T)中气液相变区(即正在发生气液转变)时,对于固定的温度,气相的压强恒为所在温度下的饱和蒸气压,即不再随体积V(严格地说应该是单位质量气体占用的体积,即比容)变化而变化,所以这种情况下范氏方程不再适用。
3与理想气体方程模拟结果的比较3.1低压状况在气体压强不太高的情况下,以下事实成立:排斥体积b 的影响相对V 而言极小,可以忽略;以二氧化碳(CO2)为例,在标准状况(0°C,1标准大气压)下,一摩尔CO2体积V 为22414 cm³,而相应的b= 43 cm³,比V 小3个数量级;分子间的距离足够大,a/V² 项完全可以视为0;譬如在一大气压下二氧化碳气体的a/V² 值只有7‰。
所以此时理想气体方程是范氏方程(也是对实际气体行为的)的一个良好近似。
分别用理想气体方程和范德瓦耳斯方程模拟的二氧化碳气体70°C时的p-V等温线3.2中高压状况随着气体压力的增加,范氏方程和理想气体方程结果的差别会变得十分明显(左图为CO2分别用理想气体方程和范德瓦耳斯方程模拟的p-V等温线,温度70°C):在压强为5000~15000kPa(50~150标准大气压)的中压区,由于体积被“压小”导致分子间距靠近,分子间的引力(表现为a/V² 项)变得不可忽略。
真实气体范德华状态方程及其修正式的改写式本文根据真实气体范德华状态方程,深入探讨真实气体范德华状态方程及其修正式的改写式,以期回答下述问题:1.什么是真实气体范德华状态方程?2.什么是它的修正式?3.如何重新改写这些方程式?答:一、什么是真实气体范德华状态方程真实气体范德华状态方程(Real Gas Van der Waals Equation of State)指的是由范德华在1873年定义的一种理论,它是为了预测气体之间的温度压力和体积变化而设计的理论。
范德华方程将气体的温度、压力和体积放在一起,以计算任何特定条件下气体的状态。
真实气体范德华状态方程(Van der Waals Equation of State for Real Gases)可以表示为:P = RT/v - a/v2 + b/v3其中R为气体常数,T是绝对温度,v是体积,a和b则是两个修正因子。
二、什么是它的修正式由于真实气体有粘性和质量,所以必须用修正因子a和b来修正温度、压力和体积的计算方法。
a和b的修正因子是由范德华自己提出的,它们用于改变气体的特性,以便更好地描述温度、压力和体积之间的关系。
a:物质的粘性因子,它表示物质分子之间的互电斥力,从而影响气体的压强。
b:质量因子,它表示每个气体分子的体积,从而对气体的体积有影响。
三、如何重新改写这些方程式由于a和b的修正因子影响到气体的特性,因此必须重新改写真实气体范德华状态方程。
现在,可以重新改写真实气体的范德华方程,使其变成:P = RT / (v - b) - a / (v2 - 2bv + b2)上述公式是根据真实气体的范德华状态方程改写出来的方程,与范德华方程类似,但可以更好地表征温度、压力和体积之间的关系。
综上所述,本文讨论了真实气体范德华状态方程及其修正式的改写式,并重新改写了真实气体的范德华方程,以更准确地描述温度、压力和体积之间的关系。
这不仅有助于增强我们对气体的了解,还使我们能够进行更准确的模拟。
瓶装气体的基础知识——气体体积与温度、压力的关系2004-5-29瓶装气体的基础知识——气体体积与温度、压力的关系气体的体积、温度、压力是确定气体状态的三个基本参数。
要研究气体物理状态的变化,进行工程上的计算,就要研究这三个基本状态参数间的关系。
而表示其三个基本状态参数间的数学关系式就是气体状态方程式,其方程式又有理想气体状态方程式和真实气体状态方程式之分。
一、理想气体状态方程式所谓理想气体,是人们为了在研究气体状态方程式时,忽略气体某些性质对基本状态参数计算的影响,而提出的一种假想的气体。
此种气体的假设条件为:1.气体分子本身不占有体积;2.气体分子间没有引力。
当实际气体的压力很低、温度较高时,由于气体的密度很小,其分子本身所占的体积与气体的全部空间之比小到可以忽略不计,而气体分子间的作用力也由于分子间的距离较大亦可忽略时,即可近似地作为理想气体进行计算。
前人曾总结出一些联系压力(P)、体积(V)、温度(T)和物质的量(n)之间关系的经验规律,现分述如下:1,波义耳-马略特定律波义耳—马略特定律可表述为:一定量的气体在等温时的容积(V)与压力(P)成反比。
即:式中:V1,V2旷:分别是定量的气体在压力Pl、P2时的容积。
2.查理定律查理定律可表述为:一定量的气体在等容时的压力(P)与热力学温度(T)成正比。
即:式中P1,P2分别是定量的气体在热力学温度T1,T2时的压力。
3,盖—吕萨克定律盖—吕萨克定律可表述为:一定量的气体在等压时的容积(V)与热力学温度(T)成正比。
即:式中T1,T2分别是定量气体在容积V1,V2时的热力学温度。
4.阿伏加德罗定律阿伏加德罗定律可表述为:在一定的温度与压力下,同体积的任何气体的摩尔数(n)相同。
即:5,理想气体状态方程理想气体状态方程(克莱庇隆方程):上述四个经验定律,总共涉及了四个变量P、V、T、n。
每一个定律反映了气体规律的一个侧面,即两参数间的关系。
综合上述四个定律,推导出P、V、T、n之间的数学关系式。
范德华(J.D.vanderwaals1837—1923)荷兰物理学家。
青年时代家境贫寒,无力入学读书。
在工作之余,刻若钻研,自学成才,1874年他的论文“论液态和气态的连续性”引起了学术界的关注。
并获得了莱顿大学的博士学位。
经过研究,他认识到如果假定气体分子不占有体积,而且分子之间不存在引力,则可从气体分子运动论得出理想气体的状态方程,但是,这两项假定不符合事实。
1881年,他给这个方程引入两个参量,分别表示分子的大小和引力,得出一个更准确的方程即范德华方程。
他还研究了毛细作用,对附着力进行了计算。
他在研究物质三态(气、液、固)相互转化的条件时,推导出临界点的计算公式,计算结果与实验结果相符。
1877—1910年任阿姆斯特丹大学教授。
1910年因研究气态和液态方程获诺贝尔物理学奖。
原子间和分子间的吸引力被命名为范德华力。
1873年他最先假设了这种力,以研究关于真实气体的理论范德华方程范德华方程是范德瓦耳斯方程的另一种翻译,简称范氏方程,是荷兰物理学家范德瓦耳斯(van der Waals,又译“范德华”、“凡德瓦耳”)于1873年提出的一种实际气体状态方程。
范氏方程是对理想气体状态方程的一种改进,特点在于将被理想气体模型所忽略的的气体分子自身大小和分子之间的相互作用力考虑进来,以便更好地描述气体的宏观物理性质。
范德华方程式具体形式为更常用的形式为(N=摩尔数)式中p为气体的压强a'为度量分子间重力的唯象参数b'为单个分子本身包含的体积v为每个分子平均占有的空间大小(即气体的体积除以总分子数量); k为波兹曼常数T绝对温度在第二个方程式里V为总体积a为度量分子间重力的参数b为1摩尔分子本身包含的体积之和b= NAb', R为普适气体常数NA为阿伏加德罗常数. 下表列出了部分气体的a,b的值范德华方程常用的形式(N=摩尔数)在一般形式的范氏方程中,常数a和b 因气体/流体种类而异,但我们可以通过改变方程的形式,得到一种适用于所有气体/流体的普适形式。
1mol范德华气体绝热膨胀做功-回复
范德华气体是一种理想气体模型,符合范德华方程。
热力学第一定律可以表示为:
ΔU = Q - W
其中,ΔU表示系统内能的增量,Q表示系统所吸收的热量,W表示系统对外做的功。
对于绝热膨胀过程,系统内没有传热(Q = 0),所以热力学第一定律可以简化为:
ΔU = -W
对于范德华气体绝热膨胀,可以利用范德华方程来描述气体的状态变化:
(P + a/V^2)(V - b) = RT
其中,P表示气体的压强,V表示气体的体积,a和b是范德华参数,R是气体常量,T是气体的温度。
当气体绝热膨胀时,压力和温度会发生变化,而体积会增大。
如果已知初始状态的P1、V1和末态的P2、V2,可以计算出气体对外做的功:W = ∫PdV
根据范德华方程,可以将P表示为V的函数,代入上式,得到:
W = ∫[(RT/(V - b)) - (a/V^2)]dV
根据范德华方程的第一项,可以使用变量替换进行积分,得到:
W = RT∫(dV/(V - b)) - a∫(dV/V^2)
对上式进行积分,并计算上下限,得到功的表达式:
W = RTln((V2 - b)/(V1 - b)) - a(1/V2 - 1/V1)
其中,ln表示自然对数函数。
所以,范德华气体绝热膨胀所做的功为RTln((V2 - b)/(V1 - b)) - a(1/V2 -
1/V1) 。