提取公因数的公式

提取公因数的公式
提取公因数的公式是数学中常见的一种运算方法，它可以帮助我们简化复杂的算式，使得计算更加方便和快捷。

在本文中，我们将详细介绍提取公因数的公式及其应用。

我们来看一下什么是公因数。

公因数是指两个或多个数共有的因数，例如，6和9的公因数是1和3。

在代数中，公因数指的是多项式中各项的公共因子，例如，2x和4x的公因数是2x。

提取公因数的公式是将多项式中各项的公共因子提取出来，从而简化多项式的运算。

具体来说，提取公因数的公式可以表示为：
a1x + a2x + … + anx = x(a1 + a2 + … + an)
其中，a1、a2、…、an是多项式中各项的系数，x是多项式中各项的公共因子。

例如，对于多项式2x + 4x + 6x，我们可以将其写成x(2 + 4 + 6)，即可得到简化后的多项式12x。

提取公因数的公式不仅可以用于简化多项式的运算，还可以用于解决一些代数方程。

例如，对于方程2x + 4 = 6x，我们可以将其转化为2x + 4x = 6，然后提取公因数得到2x(1 + 2) = 6，最后解得x = 1。

除了上述例子，提取公因数的公式还可以应用于多项式的因式分解、求解最大公因数等问题。

因此，掌握提取公因数的公式对于学习代
数和解决实际问题都非常重要。

提取公因数的公式是数学中常见的一种运算方法，它可以帮助我们简化复杂的算式，使得计算更加方便和快捷。

在学习代数和解决实际问题时，我们可以灵活运用提取公因数的公式，从而更好地理解和应用代数知识。

提取公因式这个方法实际上是运用了乘法分配律，将相同因数提取出来，考试中往往剩下的项相加减，会出现一个整数。

注意相同因数的提取。

例如：0.92×1.41＋0.92×8.59=0.92×（1.41+8.59）借来借去法看到名字，就知道这个方法的含义。

用此方法时，需要注意观察，发现规律。

还要注意还哦,有借有还，再借不难。

考试中，看到有类似998、999或者1.98等接近一个非常好计算的整数的时候，往往使用借来借去法。

例如：9999+999+99+9=9999+1+999+1+99+1+9+1—4拆分法顾名思义，拆分法就是为了方便计算把一个数拆成几个数。

这需要掌握一些“好朋友”，如：2和5，4和5，2和2.5，4和2.5，8和1.25等。

分拆还要注意不要改变数的大小哦。

例如：3.2×12.5×25=8×0.4×12.5×25=8×12.5×0.4×25加法结合律注意对加法结合律(a＋b)＋c=a＋(b＋c)的运用，通过改变加数的位置来获得更简便的运算。

例如：5.76＋13.67＋4.24＋6.33=（5.76＋4.24）＋(13.67＋6.33)拆分法和乘法分配律结这种方法要灵活掌握拆分法和乘法分配律，在考卷上看到99、101、9.8等接近一个整数的时候，要首先考虑拆分。

例如：34×9.9 = 34×(10－0.1)案例再现：57×101=？利用基准数在一系列数种找出一个比较折中的数字来代表这一系列的数字，当然要记得这个数字的选取不能偏离这一系列数字太远。

例如：2072+2052+2062+2042+2083=（2062x5）+10-10-20+21利用公式法(1) 加法：交换律，a+b=b+a,结合律，(a+b)+c=a+(b+c).(2) 减法运算性质：a-(b+c)=a-b-c,a-(b-c)=a-b+c,a-b-c=a-c-b,(a+b)-c=a-c+b=b-c+a.(3):乘法（与加法类似）：交换律，a*b=b*a,结合律，（a*b）*c=a*(b*c),分配率，（a+b）xc=ac+bc,(a-b)*c=ac-bc.(4) 除法运算性质（与减法类似）：a÷(b*c)=a÷b÷c,a÷（b÷c)=a÷bxc,a÷b÷c=a÷c÷b,(a+b)÷c=a÷c+b÷c,(a-b)÷c=a÷c-b÷c.前边的运算定律、性质公式很多是由于去掉或加上括号而发生变化的。

因式分解的常用方法第一部分：方法介绍提取公因式法、运用公式法、分组分解法和十字相乘法． 一、提公因式法.：ma+mb+mc=m(a+b+c)二、运用公式法.【知识要点】1．运用公式法：如果把科法公式反过来，就可以用来把某些多项式分解因式，这种分解因式的方法叫做运用公式法。

2．乘法公式逆变形（1）平方差公式：))((22b a b a b a -+=-（2）完全平方公式：222222)(2,)(2b a b ab a b a b ab a -=+-+=++ 3．把一个多项式分解因式，一般可按下列步骤进行： （1）如果多项式的各项有公因式，那么先提公因式；（2）如果多项式没有公因式，那么可以尝试运用公式来分解； （3）如果上述方法不能分解，那么可以尝试用。

思维导航：运用公式法是分解因式的常用方法，运用公式法分解因式的思路主要有以下几种情况： 一、直接用公式:当所给的多项式是平方差或完全平方式时，可以直接利用公式法分解因式。

例1、 分解因式：（1）x 2-9 （2）9x 2-6x+1二、提公因式后用公式:当所给的多项式中有公因式时，一般要先提公因式，然后再看是否能利用公式法。

例2、 分解因式：（1）x 5y 3-x 3y 5 （2）4x 3y+4x 2y 2+xy 3三、系数变换后用公式:当所给的多项式不能直接利用公式法分解因式,往往需要调整系数,转换为符合公式的形式,然后再利用公式法分解.例3、 分解因式：(1)4x 2-25y 2 (2)4x 2-12xy 2+9y 4四、指数变换后用公式:通过指数的变换将多项式转换为平方差或完全平方式的形式,然后利公式法分解因式,应注意分解到每个因式都不能再分解为止.例4、 分解因式:(1)x 4-81y 4 (2)16x 4-72x 2y 2+81y 4五、重新排列后用公式:当所给的多项式不能直接看出是否可用公式法分解时，可以将所给多项式交换位置，重新排列，然后再利用公式。

因式分解之提公因式和公式法因式分解是数学中的一种常见的运算方法，它可以把一个复杂的多项式表达式分解成更简单的因式乘积，从而更好地理解和运算。

一、因式分解的概念因式分解是指把一个多项式表达式写成因式的乘积形式的过程。

因式分解有两种主要的方法，一种是提公因式法，另一种是公式法。

1.1提公因式法提公因式法是指将多项式中的一个或多个公因式提取出来，使得多项式能够写成一个公因式乘以另外一个因式的形式。

提公因式法有以下几个步骤：步骤一：将多项式中的每一项按照公共因子进行分组。

步骤二：分别对每一组内的项进行因式分解，将其写成一个公因子乘以一个因式的形式。

步骤三：将每一组内的公因子提取出来，然后将每一组的因式相乘。

步骤四：将每一组的结果再相乘，得到最终的结果。

例子1：将多项式4x^2-5x+2进行因式分解。

首先，我们观察多项式，发现每一项的系数都是正整数，所以可以将多项式因式分解为最简整数.步骤一：将多项式中的每一项按照公共因子进行分组。

4x^2-5x+2=(4x^2)+(-5x)+2步骤二：分别对每一组内的项进行因式分解，将其写成一个公因子乘以一个因式的形式。

=4x(x)+(-5x)+2步骤三：将每一组内的公因子提取出来，然后将每一组的因式相乘。

=4x(x-5)+2步骤四：将每一组的结果再相乘，得到最终的结果。

=4x^2-20x+2例子2：将多项式2x^3+3x^2-4x-6进行因式分解。

步骤一：将多项式中的每一项按照公共因子进行分组。

2x^3+3x^2-4x-6=(2x^3)+(3x^2)+(-4x)+(-6)步骤二：分别对每一组内的项进行因式分解，将其写成一个公因子乘以一个因式的形式。

=2x(x^2)+3x(x)+(-4x)+(-6)步骤三：将每一组内的公因子提取出来，然后将每一组的因式相乘。

=2x(x^2+1.5x-2-3)步骤四：将每一组的结果再相乘，得到最终的结果。

=2x^3+3x^2-4x-6通过这个例子我们可以看出，当多项式中存在公因子时，提公因式法能够帮助我们简化运算过程，从而更方便地处理多项式。

因式分解——提公因式法、运用公式法【知识点】1.分解因式:把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式分解因式;2．分解因式的方法：①提公因式法 ②运用公式法。

①提取公因式法：多项式各项都含有公因式m ，可把公因式m提到外面，将多项式写成m 与的乘积形式，此法叫做提取公因式法。

提取公因式的步骤： 1）找出多项式各项的公因式 2）提出公因式 3）写成m 与的乘积形式找公因式的方法：1）公因式的系数是各项系数的最大公约数； 2）字母取各项中相同的字母； 3）相同字母的指数取次数最低的;②运用公式法：把整式相乘的乘法公式反过来，就得到因式分解的两个公式 常用公式：平方差公式： a 2－b 2=（a+b ）（a －b ）完全平方公示： a 2+2ab+b 2=（a+b ）2 a 2－2ab+b 2=（a －b ）2立方差（和）公式： a 3－b 3=（a －b ）（a 2+ab+b 2） a 3+b 3=（a+b ）（a 2－ab+b 2）运用公式分解多项式时，特别要注意多项式的系数，当多项式只有两项时，考虑用平方差公式；当多项式有三项时，考虑用完全平方公式。

【典型例题】例1.下列从左到右的变形,属于分解因式的是( )A. (x+3)(x －2)=x 2+x －6B. ax －ay+1=a(x －y)+1C. x 2－21y=(x+y 1)(x －y 1) D. 3x 2+3x=3x(x+1)例2.（1）3525x x + （2）253243143521x y x y x y +-例3.把下列各式分解因式：（1）a 2－4b 2； （2）442-+-x x（3）()()122++++b a b a （4）()()()()229262n m n m m n n m +++---例4. 把下列各式分解因式：（1）x x x ++232； （2）()222224y x y x -+【练习巩固】1.写出下列多项式中公因式（1）a 2b －5ab+9b 的公因式 . （2）x 2y(x －y)+2xy(y －x) 的公因式 .2．分解因式2x(b －a)+y(a －b)+z(b －a)= . 3.－4a 3b 2+6a 2b －2ab=－2ab( ).4.(－2a+b)(2a+3b)+6a(2a －b)=－(2a －b) ( ).5．因式分解9m 2－4n 4=( )2－( )2= 。

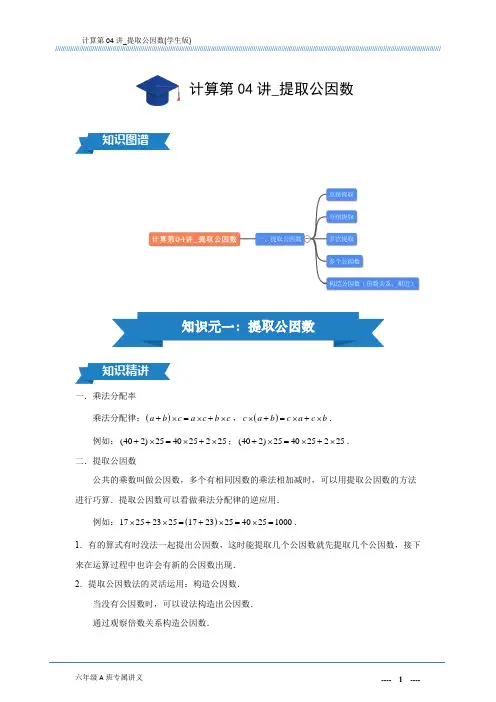
一．乘法分配率乘法分配律：()a b c a c b c +⨯=⨯+⨯，()c a b c a c b ⨯+=⨯+⨯． 例如：(402)254025225+⨯=⨯+⨯；(402)254025225+⨯=⨯+⨯． 二．提取公因数公共的乘数叫做公因数，多个有相同因数的乘法相加减时，可以用提取公因数的方法进行巧算．提取公因数可以看做乘法分配律的逆应用．例如：()1725232517232540251000⨯+⨯=+⨯=⨯=．1．有的算式有时没法一起提出公因数，这时能提取几个公因数就先提取几个公因数，接下来在运算过程中也许会有新的公因数出现． 2．提取公因数法的灵活运用：构造公因数．当没有公因数时，可以设法构造出公因数． 通过观察倍数关系构造公因数．计算第04讲_提取公因数两个因数特别接近时，可以利用加减的方法提取公因数．重难点：乘法分配律及提取公因数．题模一：直接提取例1.1.1计算：12×34-12×67+12×83=_____________． 例1.1.2计算20110002011________999-=⨯． 例1.1.32016 × 99 + 2016 =______．例1.1.4计算：45598789547895985987899⨯⨯-⨯⨯+⨯⨯=___________． 题模二：分组提取 例1.2.1计算：20162014201320152012201530132016________⨯-⨯+⨯-⨯=． 例1.2.2计算：（1）766565545443433232212110⨯-⨯+⨯-⨯+⨯-⨯； （2）5566667777888899⨯+⨯+⨯+⨯．例1.2.33737263376363⨯+⨯⨯+⨯=_____________． 题模三：多次提取例1.3.1644364486391⨯+⨯-⨯=___________．例1.3.21877112363711197752337⨯⨯+⨯⨯+⨯⨯+⨯⨯．题模四：多个公因数例1.4.1计算：11222233334444555566⨯+⨯+⨯+⨯+⨯．例 1.4.2计算：7111511725718117115549________⨯⨯+⨯⨯+⨯⨯-⨯-⨯=．285243521201440862________⨯+⨯⨯+⨯+⨯+⨯=． 1245152830266011________⨯+⨯+⨯+⨯=．例1.4.3计算：2011(911119911911)-⨯⨯+⨯⨯-⨯=_______．题模五：构造公因数（倍数关系、相近） 例1.5.1计算：1113228337⨯+⨯+⨯ 12336246173690⨯+⨯+ 9999222233333334⨯+⨯例1.5.237 × 36 + 38 × 64 = ．例1.5.33.251767.5 1.7⨯+⨯=______________．例1.5.4计算：（1）883587238612⨯-⨯-⨯；（2）12161205119311814⨯+⨯+⨯-⨯．例1.5.5234242422323⨯-⨯=______________．随练1.1计算：2613263626⨯+⨯+=___________．随练 1.2计算：（1）34773423⨯+⨯；（2）42374217⨯-⨯；（3）283228172884⨯-⨯+⨯．随练1.34864483152115222⨯-⨯+⨯+⨯=__________．随练 1.4计算：（1）71376419⨯+⨯+⨯＝___________；（2）1712917217⨯+⨯-⨯＝___________．随练1.5计算325724326881⨯⨯⨯＋＋的结果是（ ）． A ．8100 B ．6400 C ．9500 D ．8500 随练1.6562621267774⨯+⨯+⨯=_________． A ．7700 B ．770 C ．7400 D ．740随练1.7计算：233223447677⨯+⨯+⨯=_________． 随练1.8计算7531447147⨯⨯⨯⨯＋的结果是（ ）．A ．9800B ．9747C ．9753D ．9717 随练1.9计算：5566667777888899___________⨯+⨯+⨯+⨯=． 随练1.10计算12482414368⨯⨯⨯＋＋的结果是（ ）． A ．1224 B ．1220 C ．1200 D ．1248随练1.1122 × 38 + 11× 24 =__________． 随练1.1212324817________⨯+⨯=．随练1.13121324273611⨯+⨯+⨯=__________．作业11326+2639+2648=______________⨯⨯⨯．作业2计算：（1）17111721178⨯+⨯+⨯；（2）33147331003347⨯-⨯-⨯．作业3计算：（1）924910851925149108⨯+⨯+⨯+⨯；（2）⨯-⨯+⨯-⨯．12742583874584291⨯+⨯+⨯+⨯=__________．作业42226223878317833作业5766565545443433232212110⨯-⨯+⨯-⨯+⨯-⨯．作业6计算：（1）199********⨯+⨯-⨯；（2）261226172974⨯+⨯+⨯．作业7计算：（1）2614268224⨯+⨯-⨯．⨯+⨯+⨯；（2）1323118247132作业8计算：（1）17382571738132⨯⨯-⨯⨯．⨯⨯-⨯⨯；（2）3925525315作业9计算：⨯+⨯-+⨯+⨯+⨯⨯=．215101435491528251357________⨯+⨯+⨯+⨯+⨯=．33334444555566667777________作业1032476847________⨯+⨯=．作业119923661533⨯+⨯+=___________．⨯-⨯=___________．作业12计算：126117125109。

因式分解法的四种方法的公式因式分解法是一种用于解决数学问题的一种方法，用于分解某个复杂的因式，将其分解成较易于求解的若干简单的相乘的因式的乘积的方法。

从根本上讲，因式分解法是将复杂的表达式分解成若干较简单的新表达式，这些新表达式均是数学意义上有意义的因式。

显然，每种因式分解法都有其特定的步骤或公式，由此可以快速有效地完成因式分解的过程。

在因式分解法中，有四种主要的方法，它们分别是：提取公因数法、互斥因子分解法、分子式分解法和综合法。

以下详细解释了每种方法的公式。

首先是提取公因数法。

提取公因数法的公式为：将因式的项数<（变量）中的公共因子提出来，即两个因子相乘的结果，叫做公因数，如下图，它的公式为：A（X-a）×B（X -b）= A×B（X-a）（X -b）其次是互斥因子分解法。

互斥因子分解法的公式为：当因式分解时，可以将一个因式通过本质因子分解成两个因子，这两个因子相互抵消，叫做互斥因子，如下图所示，它的公式为：A（X-a）=（X -b）B第三种方法是分子式分解法。

分子式分解法的公式为：当因式分解时，如果两个因子的系数中存在一些关系，将该因式拆分为一组分子式，可以通过它们的乘积来得到原式，如下图，它的公式为：A（X-a）×B（X -b）=（A）（X-a）×（B）（X -b）最后一种方法是综合法。

综合法的公式为：因式分解时，可以将一个因式综合分解成多个因子，如下图，它的公式为：A（X-a）×B（X -b）=（A1）（X-a）×（B1）（X -b）×（A2）（X-a）×（B2）（X -b）……以上就是因式分解法的四种方法的公式。

如果用因式分解法来解决数学问题，就必须根据具体的问题选择合适的方法，用正确的公式来处理。

因式分解法是解决复杂数学问题的有效方法，它可以有效地减少复杂性，分解问题，帮助解决数学问题。

总之，因式分解法是一种数学方法，它可以将复杂的表达式分解成若干较简单的新表达式，有助于解决复杂数学问题。

乘除法巧算之提取公因数与组合思想三年级计算中的提取公因数法是近几年来数学解题能力展示、希望杯和小升初中经常考的题目，但是通过分析我们发现在考试中不仅仅是只考提取公因数这样简单的题。

这类题目往往是同和、差、积和商不变的性质进行解题。

常用的提取公因式的方法有三种：⑴直接提取公因数例如：35⨯8-35+3⨯35⑵逐步提取公因数例如：计算：2000⨯1999-1999⨯1998+1998⨯1997-1997⨯1996+1996⨯1995-1995⨯1994 ⑶利用和、差、积和商不变性质和不变性质：如果一个加数增加(减少)一个数，另一个加数减少(增加)相同的数，它们的和不变；差不变性质：如果被减数增加(减少)一个数，减数也增加(减少)相同的数，则它们的差不变；积不变性质：如果一个因数扩大几倍，另一个因数缩小相同的倍数，它们的积不变；(零除外)商不变性质：如果除数和被除数同时扩大或缩小相同的倍数，它们的商不变。

(零除外)【例1】计算：(2⨯5-9)+(2⨯6-8)+…+(2⨯9-5) 7816⨯145+314⨯2184+169⨯7816【例2】计算：(873⨯477-198)÷(476⨯874+199) 512⨯81+11⨯925+537⨯19 314⨯36+64⨯439【例3】计算：53⨯57-47⨯43 19945⨯79+12⨯158+2449197⨯63+4792+409⨯21+9521⨯479【例4】计算：2008⨯20072006-2006⨯20072008【例5】计算：333⨯332332333-332⨯333333332 1991⨯199219921992-1992⨯199119911991 〖答案〗【例1】 35 【拓展】3140000 【例2】⑴1，⑵61850 【拓展】 39400 【例3】⑴1000，⑵1580000 【拓展】4811000 【例4】 40140000【拓展】40140000 【例5】 665 【拓展】0。

提取公因式公因式是多项式中可以提取出来的一个公共因子。

在多项式的因式分解、化简和求导等计算中，提取公因式是一个常用的方法。

一.基本概念多项式是由一系列代数符号及其系数运算所得到的式子。

每一项由一个常数和一个字母的幂组成。

例如，多项式3x^2−5xy+2y^2中的每一项都是一个单项式。

二.公因式的定义给定一个多项式表达式，如果存在一个公共因子，即该多项式中的所有项都可以被这个公共因子整除，那么这个公共因子就是该多项式的一个公因式。

例如，对于多项式6x^2y+9xy^2，公因式6xy即可整除多项式中的每一项，因此6xy是这个多项式的一个公因式。

三.提取公因式的步骤提取公因式的步骤如下：1. 将多项式中的每一项拆分成其因子的乘积形式。

2. 找出所有项中的公共因子。

3. 将这个公共因子提取出来，作为提取公因式的结果。

例如，对于多项式3x^2+6xy，首先将每一项拆分为其因子的乘积形式：3x^2=x*x*3，6xy=2*3*x*y。

然后找出这两个项中的公共因子3x，将其提取出来，得到3x(x+2y)。

四.整数的公因式对于整数的公因式提取，只需要找出这些整数的所有约数，并找出它们的最大公约数作为公因式即可。

五.多项式的公因式提取方法对于多项式的公因式提取，可以借助算法来进行。

一种常见的方法是使用因式分解方法。

通过观察多项式中的每一项，找出其中的公因子，然后进行提取。

六.示例例如，对于多项式6x^2y+9xy^2，我们可以观察到每一项都包含因子3xy。

因此，我们可以将3xy提取出来，得到3xy(2xy+3y)作为提取公因式的结果。

七.提取公因式的应用提取公因式是代数中一个非常有用且常见的技巧。

它可以在因式分解、整理和化简等计算中起到简化计算和找出规律的作用。

通过提取公因式，可以将复杂的多项式化简为更简单的形式，从而更方便地进行进一步的计算和分析。

八.总结提取公因式是多项式运算中常见的一种技巧，可应用于因式分解、化简和求导等计算中。

因式分解的四种方法一、引言因式分解是数学中的一个重要概念，指将一个多项式表达式分解成更简单的乘积形式。

在高中数学中，因式分解是一个重要的章节，也是许多其他数学概念的基础。

本文将介绍四种常见的因式分解方法，包括公因数法、提公因式法、配方法和根与系数法。

二、公因数法1.定义公因数法是指在多项式表达式中找到所有项共有的因子，并将其提取出来，从而得到一个更简单的乘积形式。

2.步骤（1）找出所有项共有的最大公因数；（2）用最大公因数除去每一项中相同的部分；（3）将剩余部分相乘。

3.示例例如：$6x^2+12x$。

（1）找出所有项共有的最大公因数：$6x$；（2）用最大公因数除去每一项中相同的部分：$6x(x+2)$；（3）将剩余部分相乘：$6x(x+2)$。

三、提公因式法1.定义提公因式法是指在多项式表达式中找到可以整除所有项的一个或几个常量或变量，并将其提取出来作为公因式，从而得到一个更简单的乘积形式。

2.步骤（1）找出所有项的公因式；（2）将公因式提取出来，剩余部分相乘。

3.示例例如：$2x^3+4x^2$。

（1）找出所有项的公因式：$2x^2$；（2）将公因式提取出来，剩余部分相乘：$2x^2(x+2)$。

四、配方法1.定义配方法是指通过适当的变形将多项式表达式转化为两个容易因式分解的二次多项式之和或差的形式，从而得到一个更简单的乘积形式。

2.步骤（1）将多项式表达式按照一定规则进行拆分；（2）利用二次多项式之和或差公式进行化简；（3）将化简后的结果进行合并得到最终结果。

3.示例例如：$x^2+6x+5$。

（1）将$x^2+6x+5$拆分为$(x+5)(x+1)$；（2）利用二次多项式之和公式$(a+b)^2=a^2+2ab+b^2$进行化简，得到$(x+5)(x+1)$；（3）将化简后的结果进行合并得到最终结果：$(x+5)(x+1)$。

五、根与系数法1.定义根与系数法是指通过求出多项式的根或零点，并利用这些根或零点的特殊性质，将多项式表达式分解成更简单的乘积形式。

求公因数的公式公因数是指能够整除给定数的公共因数，也就是能够同时整除两个或多个数的因数。

在数学中，求公因数是一个常见的问题，它在因式分解、最大公因数等数学概念中都有重要的应用。

本文将介绍一种简单而有效的方法来求解公因数，帮助读者更好地理解和应用这一概念。

在求解公因数的问题中，我们首先需要找到给定数的所有因数。

因数是能够整除给定数的数，也就是能够被给定数整除的数。

例如，对于数10来说，它的因数有1、2、5和10。

一旦我们找到了两个或多个数的所有因数，就可以找出它们的公因数了。

在求解公因数的过程中，一个常见的方法是列举出所有的因数，然后找出它们的公共部分。

例如，对于数12和18来说，它们的因数分别是1、2、3、4、6、12和1、2、3、6、9、18。

我们可以观察到，它们的公因数是1、2、3和6。

这些公因数既能整除12，也能整除18，因此它们是12和18的公因数。

除了列举因数的方法外，我们还可以使用更高效的方法来求解公因数。

这个方法是通过求解给定数的素因数分解来找到公因数。

素因数分解是将一个数分解为若干个素数的乘积的过程。

素数是只能被1和自身整除的数，例如2、3、5、7等。

通过素因数分解，我们可以将一个数表示为多个素数的乘积，然后找出它们的公共部分。

例如，对于数24和36来说，它们的素因数分解分别为24=2*2*2*3和36=2*2*3*3。

通过观察这两个分解式，我们可以发现它们的公因数是2和3。

这是因为这两个数都包含了2和3这两个素因数，所以它们是24和36的公因数。

通过以上的方法，我们可以求解任意两个或多个数的公因数。

无论是列举因数还是使用素因数分解，都可以有效地找出这些数的公因数。

求解公因数是数学中的一个基本概念，它在解决问题和推导结论时都有很大的作用。

总结起来，求解公因数的公式可以通过列举因数或使用素因数分解来实现。

通过这些方法，我们能够找到任意两个或多个数的公因数，从而解决问题和推导结论。

掌握求解公因数的方法对于理解和应用数学概念非常重要，希望本文的介绍能够帮助读者更好地理解和应用这一概念。

小学数学辅导：提取公因数的方法【编者按】查字典数学网小升初为大家收集整理了小学数学辅导：提取公因数的方法供大家参考，希望对大家有所帮助!
提取公因数是我们小学数学中的要点，掌握这个要点知识，我们小学数学解题能力就能得到大大提高。

下面，我们就一起来了解一下小学数学中的这部分要点。

小学数学中的重点：提取公因数
【点拨】：乘法分配率的反应用，出错率比较高，一般包括三种类型。

(1)直接提取
例 3.6523+3.6577
【分析】：这道题比较简单，利用乘法分配律的反向应用，直接提取公因数3.65就行了。

【解答】原式=3.65(23+77)=3.65100=365
(2)省略1的题目
例6.3101-6.3
【分析】：把算式补充完整，6.3101-6.31，学生就很容易看出两个乘法算式中有相同的因数6.3
【解答】原式=6.3(101-1)=6.3100=630
(3)积不变规律(主要是小数点的变化)
例6.32.57+25.70.37
【分析】可根据乘法积不变性质，一个因数扩大，一个因数缩小相同的倍数，积不变把25.70.37转化成2.573.7，两部分就有了相同的因数2.57，创造出了可以用乘法分配律的条件。

【解答】原式=6.32.57+2.573.7=2.57(6.3+3.7)=25.7
以上这些就是小学数学中的提取公因式的方法，掌握这些重要的内容，我们的小学数学成绩才能不断提升。

因此，希望大家能够多多理解小学数学中的这些最为关键的重点内容。

提取公因数是什么定律
提取公因式a*b+a*c=a*（b+c），两个数有公共因数时可以提取公因数，取几个数的公因数，首先提出它们共同的质数因子，也就是提出公约数，比如45、54、66这三个数，首先提出3，得到15、18、22，然后没有公约数了（除了1），所以它们的公因数就是3。

给定若干个整数，如果有一个（些）数是它们共同的因数，那么这个（些）数就叫做它们的公因数。

而全部公因数中最大的那个，称为这些整数的最大公因数。

公约数与公倍数相反，就是既是A的约数同时也是B的约数的数，12和15的公约数有1，3，最大公约数就是3。

再举个例子，30和40，它们的公约数有1，2，5，10，最大公约数是10。

公因数，又称公约数。

在数论的叙述中，如果n和d都是整数，而且存在某个整数c，使得n=cd，就说d是n的一个因数，或说n是d的一个倍数，记作d|n（读作d整除n）。

如果d|a且d|b，我们就称d是a和b的一个公因数。

根据裴蜀定理，对每一对整数a，b，都有一个公因数d，使得d=ax+by，其中x和y是某些整数，并且a和b的每一个公因数都能整除这个d。

于是d的绝对值叫做最大公因数。

求几个整数的最大公因数，只要把它们的所有共有的质因数连乘，所得的积就是它们的最大公因数。