下载文档原格式
大跨度斜拉桥动力特性实测摘要：为了研究某跨海大桥的半漂浮体系斜拉桥的动力特性，对该斜拉桥进行了动力特性实测，通过对实测信号的分析，得到该大桥的固有频率和阻尼比。
关键词：斜拉桥；动力特性；固有频率；阻尼比0引言斜拉桥由于其跨越能力大、结构新颖高效而成为现代桥梁工程中发展最快、最具有竞争力的桥型之一【1】，特别是在跨江跨海大桥这面优势更加巨大。
随着科技的发展，从近年来所建的斜拉桥来看，斜拉桥的建造正在向着跨度越来越大，主梁越来越轻柔方向发展。
斜拉桥跨度增大，主梁轻柔导致其刚度变小，对桥梁在车辆荷载、风荷载和地震荷载作用下动力响应尤为敏感，严重的会引起桥梁结构的破坏。
因而有必要对其动力特性进行研究，为其抗震、抗风设计提供依据和参考，是一项很有意义的工作【2】。
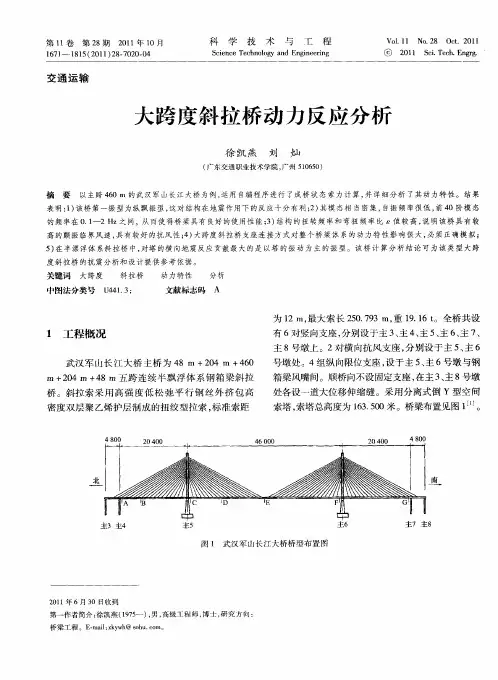
1 工程概括某跨海大桥主桥为主跨780m的五跨连续半漂浮体系双塔双索面斜拉桥，其跨径布置为95+230+780+230+95=1430m。
索塔采用钻石型，包括上塔柱、中塔柱、下塔柱、和下横梁，塔柱采用空心箱型断面，采用C50混凝土，塔柱顶高程230.70m。
主桥斜拉桥钢箱梁含风嘴全宽38m，不含风嘴宽34.108m，中心线高度3.5m。
主桥斜拉索采用1670 MPa平行钢丝斜拉索，全桥共25×4×2=200根斜拉索。
2 测试系统简介为了分析大桥的动力特性，本次实测选取了4个加速度传感器。
分别测量大桥的竖向振动和横向振动，加速度传感器布置在跨中截面，传感器布置位置如图1。
由于此次没有布置扭转加速度传感器，故扭转加速度信号则由这两个竖向加速度信号的差值除以其横向间距28m。
加速度传感器采用北戴河兰德科技的BC00-19超低频振动传感器，其最低采样频率为0.1HZ；采集模块采用的是美国恩艾公司的NI-9234，其具有抗混叠滤波强、精度高等、4通道同步采集等特点。
另外，采用美国NI公司的LabviewSignlaExpress信号采集系统。
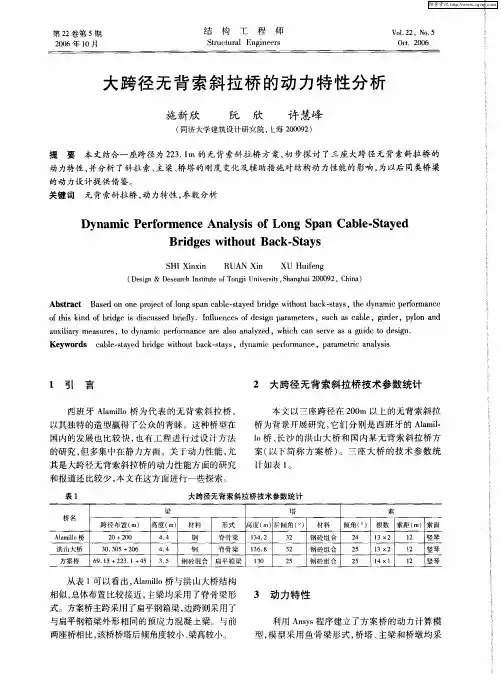
大跨度斜拉桥动力特性分析Ξ陈淮郭向荣曾庆元(郑州工业大学土建系,郑州,450002(长沙铁道学院土木系,长沙,410075摘要本文提出一种计算大跨度钢桁梁斜拉桥动力特性的方法。
文中分别采用桁段有限单元、空间梁元、空间杆元计算斜拉桥中桁架、桥塔、拉索的刚度矩阵与质量矩阵,采用子空间迭代法求解特征方程,所得结果可供设计参考。
关键词有限元法;斜拉桥;自振频率;振型分类号U 441121引言桥梁结构的动力特性包括自振频率及主振型等,它是桥梁计算的重要课题之一。
桥梁结构的动力特性反映了桥梁的刚度指标,它对于正确地进行桥梁的抗震设计及维护,有着重要的意义。
我国设计的某大跨度钢桁梁斜拉桥,这种桥型的自振频率和主振型的计算困扰着设计人员。
钢桁梁斜拉桥是一个空间杆系结构,从理论上讲计算这种结构的空间振动自振频率及主振型并不是十分困难。
然而,由于桥梁结构复杂,自由度很大,加上实际桥梁受结点及支座的约束等,完全由理论按空间梁元计算钢桁梁斜拉桥自振频率及主振型并不容易。
本文探讨这种桥型动力特性的计算方法,对于桁梁、应用桁段有限元法,将桁梁取为桁段单元,每个桁梁节间断面有10个自由度。
桥塔取为空间梁单元,每个结点有6个自由度。
斜拉桥拉索取为空间桁元,分析了国内设计中的某特大跨度斜拉桥的自振特性。
文中在形成结构总体刚度矩阵及质量矩阵时,使用形成矩阵的“对号入座”法则〔1〕,能很简便地考虑桥门架、横联等局部构件的作用。
数值算例表明,这种方法使用方便,结果可靠,结构自由度数可大大降低等优点,是斜拉桥动力分析的有效方法。
2计算模型及其主要假定211桥梁简介国内设计的某特大跨度钢桁梁斜拉桥为双塔双索面斜拉桥。
主梁采用五跨连续钢桁梁,其中主跨跨长368米,主梁宽20米,主梁高1415米,总长864米;桥塔是一个钢筋混凝土框架,塔高113米,每塔有10对索与主梁相连,构成扇形索面,桥梁简图如图1所示。
212计算模型及主要假定21211桁梁单元钢桁梁斜拉桥是一个相当复杂的结构,为了减少自由度,主桁采用桁段有限元计算,在不失对桥梁结构主要因素研究的前提下,本文采用以下主要假定:第14卷第1期计算力学学报V o l .14N o.11997年2月CH I N ESE JOU RNAL O F COM PU TA T I ONAL M ECHAN I CS February 1997Ξ河南省自然科学基金资助。
本文于1995年9月5日收到,1996年7月8日收到修改稿。
图1钢桁梁斜拉桥图2桁梁截面质量缩聚方式11除桥门架及横联外,桁梁各杆件相互铰接;21忽略上、下平纵联横撑杆的弹性轴向变形;31桥梁每个节间的质量集中在结点横截面上。
质量凝聚方法是:弦杆质量缩聚在四个角点;上、下平纵联的质量分别缩聚在上、下角点;竖杆和腹杆质量缩聚在主桁中点;桥面系和轨道、枕木质量缩聚在纵横梁的交叉点上,并同时假定横梁上各点的位移呈线性分布,由主桁下弦位移决定,主桁中点处的位移为上、下角点位移的平均值。
如图2所示。
主桁计算取4个节间梁体为一个桁段单元,共计27个桁段单元。
根据以上假定,桁梁节间断面的空间位移模式可设如图3所示。
图中,u u 、u l 分别为主桁上、下结点的横向水平位移;v u l 、v ll 、v u r 、v lr 及w u l 、w ll 、w u r 、w lr 顺次为左、右主桁架上、下结点的竖向位移及纵向位移,顺图中箭头方向的位移为正,反之为负。
所以桁段单元的结点位移参数为{∃}B =〔u u u l v u l v u r v ll u lr w u l w u r w ll w lr 〕T (121212桥塔单元根据桥塔特点,塔柱取为空间梁单元,每个塔柱取为8个空间梁单元,每个单元有2个结点,每个结点有6个自由度,所以桥塔空间梁单元的自由度为85计算力学学报14卷{∃}P =〔u ti v ti w ti Ηtx i Ηty i Ηtz i u tj v tj w tj Ηtx jΗty j Ηtz j 〕T (2(a 桁梁在其截面内的横向、竖向位移(b 桁梁横截面的纵向位移图3桁梁空间位移模式21213斜拉索单元斜拉索采用空间桁架单元,由于自重的作用,斜拉索有垂度,垂度降低了拉索的抗拉能力,这种降低效应可用E rn st 提出的等效弹性模量公式描述E eq =E1+(W L 2A E 12T 3(3式中,E eq 是考虑垂度影响后的等效弹性模量,E 是拉索的有效弹性模量,W 、L 、A 、T 分别为拉索单位长度自重、拉索水平投影长度、拉索横截面积与拉索拉力。
3振动方程的建立311斜拉桥主桁梁单元根据虚功原理,对于斜拉桥主桁系统,在任一瞬时t ,应有∆Π1+∆Πt =0(4式中,Π1为桁梁各铰接杆件的轴向变形应变能U s (桥门架及横联的楣杆不包括在内,平纵联横撑不考虑,所有横联剪切变形应变能U ci 和所有桥门架剪切变形应变能U p j 所组成,即Π1=∑s Us +∑i U ci +∑j U p j设桁梁第s 个杆件(结点为i 、j 的轴向位移分别为z i 、z j ,截面积为F ,杆长为L ,如图4所示,则其轴向变形应变能及其一阶变分为U s =E F 2L (z j -z i 2(5∆U s =E F L (z j -z i (∆z j -∆z i (6式中,∆z j 为z j 的变分,其余符号类同。
951期陈淮等:大跨度斜拉桥动力特性分析图4桁梁构件轴向变形示意图在利用上面公式计算时,可根据各杆件具体情况,计算出各端的轴向位移与桁段结点断面位移之间的关系,代入式(5、(6,即可计算出该杆的轴向变形应变能及其一阶变分。
桁梁第i 个结点横联的剪切变形由该点的横截面位移描述。
其剪切变形应变能U ci 为其竖杆与横梁的弯曲变形应变能、轴向变形应变能及各楣杆轴向变形应变能的总和。
竖杆、横梁的轴向变形能与其弯曲变形能相比很小,可以忽略,故计算横联剪切变形能时,不计竖杆轴向变形,于是由图3(a ,得横联畸变角Χ=Χ1-Χ2=u u i -u li h -(v u ri +v lri -(v uli +v lli 2b(7设横联抗剪刚度为R d ,则产生畸变角Χ的剪切力为R d h Χ。
第i 个横联剪切变形能U ci 等于剪切力所作之功,故U ci =12R d h Χ h Χ={∃1}T 12R d h 2〔N 1〕T 〔N 1〕{∃1}(8∆U ci ={∆∃1}T R d h 2〔N 1〕T 〔N 1〕{∃1}(9式中〔N 1〕=〔1h -1h 12b 12b -12b-12b〕{∃1}=〔u u i u li v u li v lli v u ri v lri 〕T {∆∃1}=〔∆u u i ∆u li ∆v u li ∆v lli ∆v u ri ∆v lri 〕T 各位移参数及其一阶变分的编号是它们在总刚度矩阵中的编号。
横联抗剪刚度R d 为横联顶边相对于底边产生单位侧向水平位移时作用于顶边的侧向水平力,简化计算时,对于图5所示中间横联,根据文献〔4〕的思想,可得横联抗剪刚度R d 为R d =24E Ih 21(c +h 1(10图5中间横联当需要精确计算R d 时,采用有限单元法计算图5所示平面框架,下端固定,当顶边产生单位侧向水平位移时,在顶边所作用的侧向水平力即为横联抗剪刚度R d 。
桥门架剪切变形时,式(9中只有其顶点侧移u u j ≠0,故第j 个桥门架剪切变形能的一阶变分为∆U p j =∆u u j R 0u u j (11上式表示:不论是竖向和斜向桥门架,只需将其抗剪刚度R 0加到与u u j 对应的总刚度矩阵主元素中,即可很方便地处理桥门架的剪切变形影响。
桁梁惯性力虚功∆Πt 系根据达朗伯原理及桥梁振动位移图3,通过计算每一结点横截面的惯性力虚功∆Πm i 最后迭加而成。
而∆Πm i 又是图2所示每个缩聚质量j 处惯性力虚功∆Πm ij 之和。
设缩聚质量m ij 的位移为d j ,则该缩聚质量的惯性力虚功为m ij dβj ∆d j ,于是∆Πt =∑i ∆Πm i =∑i ∑j m ij d βj ∆d j(12由虚功方程(4式,可方便地得到斜拉桥主桁系统的总体刚度矩阵[K ]B 和质量矩阵06计算力学学报14卷[M ]B 。
312塔柱单元本文将塔柱取为空间梁单元,单元质量矩阵采用一致质量矩阵,空间梁元的单元刚度矩阵和质量矩阵显式表达式见文献〔3〕。
组集塔柱单元的单元特性,由此可得桥塔结构的总体刚度矩阵[K ]P 和质量矩阵[M ]P 。
313斜拉索单元斜拉索采用空间桁元计算,求其轴向变形应变能及其一阶变分时,可利用公式(5、(6进行计算。
根据各斜拉索的具体情况,计算出索端的轴向位移与桁段结点断面位移及与桥塔结点位移之间的关系,代入式(5、(6,即可计算出该索的轴向变形应变能及其一阶变分。
同理求出斜拉索的惯性力虚功。
应用虚功原理及形成矩阵的“对号入座”法则〔1〕,可得斜拉索的刚度矩阵[K ]S 和质量矩阵[M ]S 。
把斜拉桥主桁系统刚度矩阵与质量矩阵、桥塔结构刚度矩阵与质量矩阵、斜拉索的刚度矩阵与质量矩阵分别扩阶迭加,即可得斜拉桥总体刚度矩阵[K ]及总体质量矩阵[M ]。
314实例验证鉴于文献〔5〕已对空间梁元模拟桥塔、空间桁元模拟斜拉索作了论证,所以本文仅就桁段有限元法计算桁梁桥结构自振特性的可行性进行验证。
用这种桁段有限元法计算了沪杭线上41号桥(跨度92196米简支下承式非平行弦钢桁梁桥等桥的自振特性,计算结果与实测结果〔6〕接近,限于篇幅,这里给出部分计算结果如表1所示,从表1可以看出,本文建议的桁段有限元法计算桁梁桥结构自振特性结果可靠,方法正确。
表1沪杭线41号桥计算自振频率与实测值对比(H Z序号频率计算值实测值振型特征1111401110侧向弯曲振动为主2215932171扭转振动为主3216812160竖向弯曲振动为主4计算结果及其分析在得到斜拉桥的总体刚度矩阵和质量矩阵后,可以得到斜拉桥结构自由振动微分方程为[M ]{∃β}+[K ]{∃}={0}(13由此可得斜拉桥结构的特征方程为〔[K ]-Ξ2[M ]〕{A }={0}(14本文使用子空间迭代法〔7〕解此方程,得出斜拉桥结构的前10阶自振频率及其主振型,并指出它们各以何种振动形式为主,计算结果列于表2,图6为用计算机给出的斜拉桥前7阶振型图。
需要说明的是由于第3、4阶主振动是以桥塔横向振动形式为主,图中没有附出。
161期陈淮等:大跨度斜拉桥动力特性分析62 计算力学学报表 2斜拉桥的自振频率和周期序号 1 2 3 4 5 6 7 8 9 10 14 卷频率 (H Z 01299 01560 01561 01568 01622 01739 01882 01888 01987 11152 周期 ( S 31349 11783 11782 11762 11609 11354 11134 11126 11013 01868 振型特征 u u 主桁横向振动为主 v l 主桁竖向振动为主 u t 桥塔横向振动为主 u t 桥塔横向振动为主 w l 主桁纵向振动为主 u u 主桁横向振动为主 v l 主桁竖向振动为主 u u 主桁横向振动为主 u u 主桁横向振动为主 v l 主桁竖向振动为主图 6斜拉桥振型图从图 6 可以看出, 该斜拉桥结构第一阶主振型图主桁上、下弦杆横向振型同向, 且振型图中间无节点, 故该振型图对应于斜拉桥结构以横向弯曲振动为主的第一阶振型。
