信号与线性系统分析吴大正第四版习题答案第六章

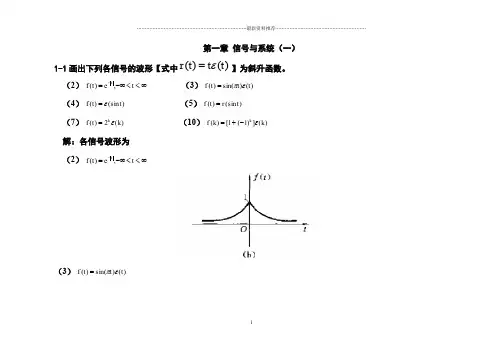
第一章 信号与系统（一）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+= 解：各信号波形为 （2）∞<<-∞=-t e t f t ,)(（3）)()sin()(t t t f επ=（4）)fεt=(sin)(t（5）)trf=(sin)(t（7）)t(kf kε=)(2（10）)f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε 解：各信号波形为 （1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

（2）)63cos()443cos()(2ππππ+++=k k k f （5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

之吉白夕凡创作（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f =（7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+=解：各信号波形为（2）∞<<-∞=-t e t f t,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)(sin )(t r t f =（7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=kkkkfεεπ（12）)]()3([2)(kkkf k---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=ttttfεεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=kkkkfεε（11）)]7()()[6sin()(--=kkkkfεεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

（2）)63cos()443cos()(2ππππ+++=k k k f （5）)sin(2cos 3)(5t t t f π+= 解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。

1 / 28专业课习题解析课程第1讲第一章 信号与系统〔一 专业课习题解析课程第2讲第一章 信号与系统〔二1-1画出下列各信号的波形[式中)()(t t t r ε=]为斜升函数。

〔2∞<<-∞=-t et f t,)( 〔3)()sin()(t t t f επ=〔4)(sin )(t t f ε= 〔5)(sin )(t r t f =2 / 28〔7)(2)(k t f kε= 〔10)(])1(1[)(k k f kε-+=解：各信号波形为 〔2∞<<-∞=-t et f t,)(〔3)()sin()(t t t f επ= 〔4)(sin )(t t f ε= 〔5)(sin )(t r t f = 〔7)(2)(k t f k ε= 〔10)(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

〔1)2()1(3)1(2)(-+--+=t t t t f εεε 〔2)2()1(2)()(-+--=t r t r t r t f 〔5)2()2()(t t r t f -=ε 〔8)]5()([)(--=k k k k f εε 〔11)]7()()[6sin()(--=k k k k f εεπ〔12)]()3([2)(k k k f k---=εε 解：各信号波形为〔1)2()1(3)1(2)(-+--+=t t t t f εεε3 / 28〔2)2()1(2)()(-+--=t r t r t r t f〔5)2()2()(t t r t f -=ε〔8)]5()([)(--=k k k k f εε〔11)]7()()[6sin()(--=k k k k f εεπ〔12)]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

第5章连续系统的s域分析一、选择题1．信号的拉普拉斯变换为（）。

【答案】C【解析】为t与u（t）的卷积，u（t）的拉氏变换为1/s，t的拉氏变换为，时域的卷积对应频域的乘积，所以×＝。

2．f（t）＝e2t u（t）的拉氏变换及收敛域为（）。

【答案】C【解析】u（t）的拉氏变换为1/s，根据频域的平移性质，x（t）jcte-←−→X（s－c）。

题中c＝2，右边信号的收敛域大于极点。

3．已知某信号的拉氏变换式为，则该信号的时间函数为（）。

A．e－α（t—T）u（t－T）B．e－αt u（t－T）C．e－αt u（t－α）D ．e －αu （t －T ） 【答案】B【解析】可采用从时域到频域一一排除的方法，u （t ）的拉氏变换为1/s,根据时移性，u （t －T ）的拉氏变换为s e sT -，再根据频域的时移性，e －αt u （t －T ）的拉氏变换为sesT-的s 左移α，即se sT-中的s 加上α。

可推断出B 项的拉氏变换为。

4．信号f （t ）＝（t ＋1）u （t ＋1）的单边拉普拉斯变换为（ ）。

【答案】B【解析】f （t ）是tu （t ）向左移1个单位时间后的结果，由于单边拉氏变换只研究0t ≥的时间函数，故不能利用性质求F （s ）。

因此可认为f （t ）与（t ＋1）u （t ）的单边拉氏变换相同，于是2111(t )u(t )s s+↔+。

5．信号u （t ）－u （t －2）的拉普拉斯变换及收敛域为（ ）。

【答案】A【解析】阶跃u （t ）的拉普拉斯变换为s1，根据拉普拉斯变换的时移性，f （t －0t ）)(0s F ets -−→←,则u （t ）的拉普拉斯变换为se s2-。

6．象函数的拉普拉斯逆变换为（ ）。

【答案】B【解析】由常用拉氏变换和拉氏变换的性质知()1(),,s sT s a T ate e u t s s s a--+-↔↔↔+时域平移u(t-T)域平移e u(t-T) 首先将F （s ）变形为：e sT T e s αα--+，e st s α+的逆变换为(t T )e u(t T )α---，T e α-为常数，所以所求的逆变换为(t T )eu(t T )α---T e α-＝t e u(t T )α--。

专业课习题解析课程西安电子科技大学844信号与系统专业课习题解析课程第1讲第一章信号与系统（一）专业课习题解析课程第2讲第一章信号与系统（二）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)fεt=(sin)(t（5）)trf=(sin)(t（7）)t(kf kε=)(2（10）)f kεk-=(k+(])1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f （5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

目　录第1章　信号与系统1.1　复习笔记1.2　课后习题详解1.3　名校考研真题详解第2章　连续系统的时域分析2.1　复习笔记2.2　课后习题详解2.3　名校考研真题详解第3章　离散系统的时域分析3.1　复习笔记3.2　课后习题详解3.3　名校考研真题详解第4章　傅里叶变换和系统的频域分析4.1　复习笔记4.2　课后习题详解4.3　名校考研真题详解第5章　连续系统的s域分析5.1　复习笔记5.2　课后习题详解5.3　名校考研真题详解第6章　离散系统的z域分析6.1　复习笔记6.2　课后习题详解6.3　名校考研真题详解第7章　系统函数7.1　复习笔记7.2　课后习题详解7.3　名校考研真题详解第8章　系统的状态变量分析8.1　复习笔记8.2　课后习题详解8.3　名校考研真题详解第1章　信号与系统1.1　复习笔记一、信号的基本概念与分类信号是载有信息的随时间变化的物理量或物理现象，其图像为信号的波形。

根据信号的不同特性，可对信号进行不同的分类：确定信号与随机信号；周期信号与非周期信号；连续时间信号与离散时间信号；实信号与复信号；能量信号与功率信号等。

二、信号的基本运算1加法和乘法f1（t）±f2（t）或f1（t）×f2（t）两信号f1（·）和f2（·）的相加、减、乘指同一时刻两信号之值对应相加、减、乘。

2．反转和平移（1）反转f（－t）f（－t）波形为f（t）波形以t＝0为轴反转。

图1-1（2）平移f（t＋t0）t0＞0，f（t＋t0）为f（t）波形在t轴上左移t0；t0＜0，f（t＋t0）为f（t）波形在t轴上右移t0。

图1-2平移的应用：在雷达系统中，雷达接收到的目标回波信号比发射信号延迟了时间t0，利用该延迟时间t0可以计算出目标与雷达之间的距离。

这里雷达接收到的目标回波信号就是延时信号。

3．尺度变换f（at）若a＞1，则f（at）波形为f（t）的波形在时间轴上压缩为原来的；若0＜a＜1，则f（at）波形为f（t）的波形在时间轴上扩展为原来的；若a＜0，则f（at）波形为f（t）的波形反转并压缩或展宽至。

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

之樊仲川亿创作（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f =（7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+=解：各信号波形为（2）∞<<-∞=-t e t f t ,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)(sin )(t r t f =（7）)(2)(k t f k ε=（10）)(])1(1[)(k k f k ε-+= 1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=kkkkfεε（11）)]7()()[6sin()(--=kkkkfεεπ（12）)]()3([2)(kkkf k---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=ttttfεεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=kkkkfεε（11）)]7()()[6sin()(--=kkkkfεεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

（2）)63cos()443cos()(2ππππ+++=kkkf（5）)sin(2cos3)(5tttfπ+=解：1-6 已知信号)(tf的波形如图1-5所示，画出下列各函数的波形。

. 学习参考. 第六章6.4 根据下列象函数及所标注的收敛域，求其所对应的原序列。

（1）1)(=z F ，全z 平面（2）∞<=z z z F ,)(3（3）0,)(1>=-z z z F（4）∞<<-+=-z z z z F 0,12)(2（5）a z az z F >-=-,11)(1（6）a z az z F <-=-,11)(1. 学习参考.6.5 已知1)(↔k δ，az z k a k -↔)(ε，2)1()(-↔z z k k ε，试利用z 变换的性质求下列序列的z 变换并注明收敛域。

. 学习参考 .（1）)(])1(1[21k k ε-+ （3）)()1(k k k ε-（5）)1()1(--k k k ε （7）)]4()([--k k k εε（9）)()2cos()21(k k k επ. 学习参考.6.8 若因果序列的z 变换)(z F 如下，能否应用终值定理？如果能，求出)(lim k f k ∞→。

（1）)31)(21(1)(2+-+=z z z z F （3）)2)(1()(2--=z z z z F. 学习参考.6.10 求下列象函数的双边逆z 变换。

（1）31,)31)(21(1)(2<--+=z z z z z F （2）21,)31)(21()(2>--=z z z z z F （3）21,)1()21()(23<--=z z z z z F. 学习参考 .（4）2131,)1()21()(23<<--=z z z z z F. 学习参考.. 学习参考.. 学习参考.. 学习参考.6.11 求下列象函数的逆z 变换。

（1）1,11)(2>+=z z z F （2）1,)1)(1()(22>+--+=z z z z z z z F （5）1,)1)(1()(2>--=z z z z z F （6）a z a z az z z F >-+=,)()(32. 学习参考.. 学习参考.. 学习参考.6.13 如因果序列)()(z F k f ，试求下列序列的z 变换。

1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)f=rt)(sin(t （7）)t(k=f kε)(2（10）)f kεk=(k+-((])11[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

（2）)63cos()443cos()(2ππππ+++=k k k f （5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。

1-1画出以下各信号的波形【式中)()(t t t r ε=】为斜升函数。

〔2〕∞<<-∞=-t et f t,)( 〔3〕)()sin()(t t t f επ=〔4〕)(sin )(t t f ε= 〔5〕)(sin )(t r t f = 〔7〕)(2)(k t f kε= 〔10〕)(])1(1[)(k k f kε-+=解：各信号波形为 〔2〕∞<<-∞=-t et f t,)(〔3〕)()sin()(t t t f επ=〔4〕)(sin )(t t f ε=〔5〕)f=rt)(sin(t〔7〕)t=(kf kε(2)〔10〕)f kεk=(k+-((])1)1[1-2 画出以下各信号的波形[式中)()(t t t r ε=为斜升函数]。

〔1〕)2()1(3)1(2)(-+--+=t t t t f εεε 〔2〕)2()1(2)()(-+--=t r t r t r t f〔5〕)2()2()(t t r t f -=ε 〔8〕)]5()([)(--=k k k k f εε〔11〕)]7()()[6sin()(--=k k k k f εεπ〔12〕)]()3([2)(k k k f k ---=εε解：各信号波形为〔1〕)2()1(3)1(2)(-+--+=t t t t f εεε〔2〕)2()1(2)()(-+--=t r t r t r t f〔5〕)2()2()(t t r t f -=ε〔8〕)]5()([)(--=k k k k f εε〔11〕)]7()()[6sin()(--=k k k k f εεπ〔12〕)]()3([2)(k k k f k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别以下各序列是否为周期性的。

如果是，确定其周期。

〔2〕)63cos()443cos()(2ππππ+++=k k k f 〔5〕)sin(2cos 3)(5t t t f π+=解：1-6 信号)(t f 的波形如图1-5所示，画出以下各函数的波形。

第一章 信号与系统（一）1-1画出下列各信号的波形【式中)()(t t t r ε=】 为斜升函数。

（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+= 解：各信号波形为 （2）∞<<-∞=-t e t f t ,)(（3）)()sin()(t t t f επ=（4）)fεt=(sin)(t （5）)tf=r(sin)(t（7）)tf kε(k=(2)（10）)f kεk-=(k+]()1(1[)1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε 解：各信号波形为 （1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t rt rt rtf（5）)2()2()(ttrtf-=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

（2）)63cos()443cos()(2ππππ+++=k k k f （5）)sin(2cos 3)(5t t t f π+=解：1-6 已知信号)(t f 的波形如图1-5所示，画出下列各函数的波形。