《边角边判定定理》PPT教学课件

（2）探究：根据题目所给数据把这个三角形补全， 和同学对比一下，看是否完全重合？
450
12cm
600
第3页/共15页
：
有两角及其夹边对应相等的两个三角 形全等(简写成“角边角”或“ASA”）。
A
符号语言表示
在△ABC和△
中
∵ ∠A=∠ （A已 知 ）
AB= A（B已 知 ）
∠B=∠ （已知 ）
B
∴ △ABC≌△
∵
AC=AB（已知） ∠C=∠B（已知）
B
DE
A
C
∴△ADC≌△AEB（ASA） ∴AD=AE（全等三角形的对应边相等） 又∵AB=AC（已知）
∴AB-AD=AC-AE即BD=CE（等式性B 质）
第12页/共15页
D O
B
E C
小测：如图，AB⊥BC，AD⊥DC， ∠1=∠2。 求证AB＝AD。 A
∴△ADC≌△BOD（ ）
B C
2.如图在，△AOC和△BOD中
∠A=∠B（已知）
∵
（
）
CA=DB （已知）
∴△ADC≌△BOD（ ）
O D
A
第11页/共15页
例2已知：点D在AB上，点E在AC上，BE和CD相交于
点O，AB=AC，∠B=∠C。
求证：BD=CE
A
A
证明 ：在△ADC和△AEB中
∠A=∠A（公共角）
证明： 在△ABD和△ABC中
D
∠D=∠C（已知）
∠1=∠2 （已知）
∵ AB=AB（公共边）
1
∴△ABD≌△ABC （AAS）
A2
B
∴AC=AD （全等三角形对应边相等）
C

自主探究时间：2分钟 小组合作探究及展示时间：4分钟 点评时间：2分钟； 提前完成的同学可思考训练案第3题
展示问题 探究二
展示小组 第5小组
点评和补充 第8小组
质疑和总结 全班同学
展示要求： 展示同学：快速，书写认真规范，简洁； 非展示同学：在同学展示时继续讨论或整理总结，准备好补 充、质疑；
点评要求： 点评同学：1、先分析解题思路，再规范步骤，总结易错点， 及规律方法； 2、点评注重教态：语言简洁准确，富有逻辑，声音洪亮， 3、点评讲究效率，与同学互动。 非点评同学：认真倾听，积极思考，重点内容记好笔记，有 不明白或有补充的大胆提出。
提前完成的同学可完成训练案第3题
限时4分钟
如图，AB=AD，要说明 ∆ABC≌∆ADC , 只需补充____=____ ，依据是________.
规则：当老师说 “抢答开始”后， 最先起立的同学获 得答题机会，回答 正确后可获神秘礼
探究一：小组合作探究时间：4分钟
1. 动手操作：小组一起合作画一个∆ABC使
得 A 30， AB=18cm，BC=10cm，并将所
画三角形剪下来。（每个小组完成一件作品）
要求：各小组需在4分钟内把剪好的三角形展 示在各小组的展示区上。提前完成的小组观察别 的小组所拼三角形是否都一样？并思考这能得出 什么结论？
下列条件中不能判定 ≌
A．
，
，
B．
，
，
C．
，，D．， Nhomakorabea，
的是（ C ）
探究二：综合知识应用探究
2. 点A,E,B,D在同一直线上，AE=DB,AC=DF, AC∥DF.请探索BC与EF有怎样的位置关系，并 说明理由 .

把你画的三角形与其他同学画的三角形进行比较， 那么所有的三角形都全等吗？此时符合条件的三角 形的形状能有多少种呢？
用“两边一角”证明三角形全等时， 那个“角”必须是“两边”的夹角
学以致用
例：点E、F在AC上，AD//BC，AD=CB，AE=CF
求证：△AFD≌△CEB A
D
E
分析：证三角形全等的三个条件 B
\\
B
\
｛
A
D
因为AB=DE，∠B=∠E，
\\Байду номын сангаас
BC=EF，
CE
\
根据“SAS”可以得到 F △ABC≌△DEF
在△ABC和△ DEF中，
小试身手
例1如图19.2.4，在△ABC中，AB＝AC， AD平分 ∠BAC，求证： △ABD≌△ACD．
如图，已知两条线段和一个角，以长的线段为已 知角的邻边，短的线段为已知角的对边，画一个 三角形．
在△AOC和△BOD中 ∵ AC= BD ，
AO= BO ， CO= DO ，
∴ △AOC≌△BOD（SSS）
A
D
O
C
B
如图19.2.2，已知两条线段和一个角，以这两条线段 边，以这个角为这两条边的夹角，画一个三角形．
步骤： 1 画一线段AB， 使它等于4cm； 2 画∠MAB＝45°； 3 在射线AM上截取AC＝3cm； 4 连结BC．
△ABC即为所求．
1 你们所画的三角形有什么共同特征？ 有两边及其夹角对应相等
2 把你画的三角形与其他同学画的三角形 进行比较，所有的三角形都全等吗？
在△ABC和△A′B′C′中，已知AB＝A′B′， ∠B＝ ∠B′， BC＝B′C′
A

AD=AD ∴ △ABD ≌△ACD
思考：从△ABD ≌△ACD中，你还能证得哪些结论？
知识应用:
A
B
④
互动3：
已知两条线段和一个角，以长的线段为已知角的邻边，短 的线段为已知角的对边，画一个三角形。
问题：把所画的三角形进行比较，那么所有的三角形都全 等吗？此时符合条件的三角形的形状能有几种呢?
九年义务教育初中数学课件
问题引入：
1、回顾上节课所学的内容，考虑如果两个三角形有三组对应 相等的元素，那么它可以分为几种情况？
两边一角、两角一边、三角、三边
2、如果两个三角形有两条边和一个角分别对应相等，那么它 有几种情况？
（边——角——边）
（边——边——角）
探互究动新1：知：
如图所示，已知两条线段和一个角，以这两条线段为边，以这个角为这
概括：有两条边及其中一边的对角对应相等的两个三角 形不一定全等 判断：有两条边和一个角对应相等的两个三角形全等。
学习目标：
1、掌握运用“边角边”判定两个三角形全等的方法。
两两条边边 一角的、夹两角角，2一画、边出、一经三个角三历、角三形探边。 索“两边一角”三角形全等条件的过程，体会如 何探索研究问题，增强合作意识 问题：把所画的三角形进行比较，那么所有的三角形都全等吗？此时符合条件的三角形的形状能有几种呢?
归纳：如果两个三角形有＿两＿边及其＿夹＿角分别对应相等，那么 这两个三角形全等。简记为＿边＿角＿边（ S、A、S ）
互例1动：2如：图，在△ABC中，AB=AC,AD平分∠BAC,
求证： △ABD ≌△ACD
证明： ∵ AD平分∠ BAC
∴ ∠BAD= ∠ CAD 在△ABD和△ACD中,
AB=AC ∠BAD=∠ CAD

对《三角形全等的判定——边角边》的说明
精选版课件ppt
1
教材分析
精选版课件ppt
2
教材内容
本节课是人教版教材八年级上册第十一章第 二节第二课时----《三角形全等的判定----边角 边》
精选版课件ppt
3
内容解析
核心知识：
两个三角形全等的条件----边角边
课标要求：
探索并掌握两个三角形全等的条件。
精选版课件ppt
6
学情分析
精选版课件ppt
7
●知识经验：
学生在前一课时经历了探索两个三角形 全等的条件----边边边的过程，具备了利用 画图的方法构造全等三角形的活动经验，并 且对研究几何命题的过程有了初浅的认识。 但是可能有个别学生会完全照搬“边边边”， 而忽略两种方法的区别。
精选版课件ppt
充分问题思考，大胆交流观点，让学生明确 了本节课的核心内容，同时调动学生的思考积极
性，激起求知欲望。
精选版课件ppt
20
环节三
A
已知△ABC， 画△DEF，使ED=BA , EF= BC,∠E=∠B
B M
D
(怎样画△DEF？)
要求：1、利用手中工具
E
2、剪下所画的△DEF，放到△ABC上，观察是否
2、用数学语言表述
精选版课件ppt
23
设计意图:
学生的语言表述不够准确，但充分暴露了对边角 边命题的认识和理解，又能够对学生的抽象概括能力 和语言表达能力进行培养，同时类比思想方法得到渗 透。
在符号翻译的过程中，可以让学生对命题的具体 条件和结论有更进一步的深化丰富。至此，学生能够 根据边角边定理判定两个三角形全等。
环节六
1 本节课你有什么收获和感悟？ 2 请构建本节课的知识框架？

C
证明:
△ACB ≌ △ADB A
B
这两个条件够吗?
D
10
例1
已知: 如图,AC=AD ,∠CAB=∠DAB. 求证: △ACB ≌ △ADB.
C
证明:
△ACB ≌ △ADB. A
B
这两个条件够吗?
还要什么条件呢?
D
11
例1
已知: 如图,AC=AD ,∠CAB=∠DAB. 求证: △ACB ≌ △ADB.
C
证明:
△ACB ≌ △ADB. A
B
这两个条件够吗?
还要什么条件呢?
还要一条边
D
12
例1
已知: 如图,AC=AD ,∠CAB=∠DAB. 求证: △ACB ≌ △ADB.
C
证明: 在△ACB 和 △ADB中
AC = A D (已知) A
B
∠CAB=∠DAB（已知）
A B = A B (公共边）
∴△ACB≌△ADB（SAS） D
第十二章全等三角形
12.2 三角形全等的判定 （边角边）
1
我们学过哪几种判定三角形全等的方法？
1、全等三角形概念：三条边对应相 等，三个角对应相等。 2、全等三角形判定条件（一） 三边对应相等的两个三角形全等。 简称“边边边”或“SSS”
2
问题:如图有一池塘。要测池塘两端A、B的距离，可 无法直接达到，因此这两点的距离无法直接量出。你能想 出办法来吗？
6
三角形全等判定方法2
两边和它们的夹角对应相等的两个三角形全
等。(可以简写成“边角边”或“SAS”)
用符号语言表达为： 在△ABC与△DEF中
A
D
AC=DF ∠C=∠F BC=EF

202夹边解该三角形 例题： 在球面三角形中， 已知 a＝50°44′.0，
B＝ 69°12′.0， C＝115 °55 ′.4， 求 c。 应用四联公式：边的外余切内正弦等于角的 外余切内正弦加上双内余弦之积
ctgcsina=ctgCsinB+cosacosb
2020/12/10
1
证明AAS： AAS,即角角边，已知两个三角形对应的两个角和其中一个角的对边，问两个
三角形是否全等？或已知两个角和其中一个角的对边，问此三角形是否唯一。 首先已知两个角，也可以算出第三个角的度数，再根据ASA证明三角形全等。 证明方法如下：∵已知∠a与∠b，∠a+∠b+∠c=180°∴得知∠c ∵已知∠a，线段C，∠c， 所以三角形是唯一（ASA）。 在AAS中， 已知AA两个角，根据三角形内角和等于180°，可以证明剩下的一对角相等 然后因ASA可证明三角形全等，
所以AAS也可以证明三角形全等。
2020/12/10
2
举例：如下图，AB平分∠CAD， AC=AD，求证∠C=∠D. 证明：∵AB平分∠CAD.
∴∠CAB=∠BAD. 在△ACB与△ADB中{AC=AD， ∠CAB=∠BAD，AB=AB. ∴△ACB≌△ADB.（SAS） ∴∠C=∠D.（全等三角形的对应角 相等）
2020/12/10
4
应用的时候要注意使用正确 的方法
2020/12/10
5
2020/12/10
6

培养逻辑思维
掌握全等三角形判定定理 对于培养学生的逻辑思维 和推理能力具有重要意义。
角边角判定定理在几何证明中的应用
解决实际问题
角边角判定定理在解决实际问题中发 挥着重要作用，如测量、计算等领域。
提高解题效率
掌握角边角判定定理有助于提高解题 效率，帮助学生更快地解决几何问题。
简化证明过程
使用角边角判定定理可以简化几何证 明的步骤，使证明过程更加简洁明了。
总结词
直角三角形全等判定定理的应用
详细描述
在直角三角形中，如果两个直角边和夹角相等，则两个三角形全等。 这个判定定理可以用于证明两个直角三角形是否全等。
实例分析
假设我们有两个直角三角形ABC和DEF，其中∠C=∠F=90°，AC=DF， AB=DE，并且∠A=∠D。根据角边角判定定理，我们可以得出 △ABC≌△DEF 。
在复杂的几何图形中，识别并证明满足角边 角定理的全等三角形。
练习3
解决涉及角边角定理的实际问题，如测量、 构造等。
05
总结与回顾
全等三角形判定定理的重要性
01
02
03
几何证明的基础
全等三角形判定定理是几 何证明中的基础工具，是 解决各种几何问题的关键。
实际应用
在实际生活中，全等三角 形判定定理的应用也非常 广泛，如建筑设计、机械 制造等领域。
04
角边角判定定理的练习题
基础练习题
01
02
03
04
总结词
理解角边角判定定理的基本应 用
练习1
给出两个三角形，其中一个角 和两条边相等，判断这两个三
角形是否全等。
练习2
根据给定的条件，构造一个全 等三角形。

D B
C
质疑再探
对于本节课学习的知识， 大家有什么疑问，请大 胆提出来
怎么办？可以帮帮我 吗？
如图,小明不慎将一块三 角形模具打碎为三块,他是否 可以只带其中的一块碎片到 商店去,就能配一块与原来一 样的三角形模具吗? 如果可 以,带哪块去合适?你能说明 其中理由吗?
①
②
③
A
1、在△ABC 和△A′B ′C ′中 已知 ∠A = ∠A′ ，AB = A′B ′
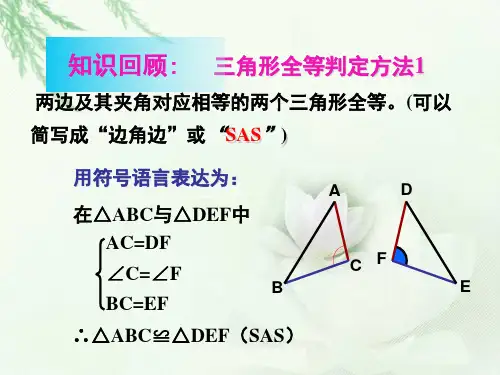
知识回顾: 三角形全等判定方法1
两边及其夹角对应相等的两个三角形全等。(可以
简写成“边角边”或“SAS”)
用符号语言表达为： 在△ABC与△DEF中
A
D
AC=DF ∠C=∠F BC=EF
CF
B
E
∴△ABC≌△DEF（SAS）
创设情景,实例引入
怎么办？可以帮帮我 吗？
如图,小明不慎将一块三 角形模具打碎为三块,他是否 可以只带其中的一块碎片到 商店去,就能配一块与原来一 样的三角形模具吗? 如果可 以,带哪块去合适?你能说明 其中理由吗?
∠B=∠C（已知） ∴ △ABE≌△ACD(A.S.A.)B
E O
C
例3 已知：如图，点A，F，E，C在同一条直线上， AB∥DC，AB=CD，∠B=∠D.
求证：△ABE≌△CDF.
证明 ∵ AB∥DC， ∴ ∠A=∠C. 在△ABE和△CDF中， ∠A=∠C， AB = CD， ∠B=∠D， ∴ △ABE≌△CDF （A.S.A.）.
C
∠ABC＝∠DCB（已知）
BC＝CB（公共边）
∠ACB＝∠DBC（已知）
∴ △ABC≌△DCB（ A.S.A）.
例2、已知：点D在AB上，点E在AC上，BE和

总结
(1)在证两三角形全等所需要的角相等时，通常 采用的目前所学过的方法有：(1)公共角、对顶角分 别相等；(2)等角加(减)等角，其和(差)仍相等，即 等式的性质；(3)同角或等角的余(补)角相等；(4)角 平分线得到相等角；(5)平行线的同位角、内错角相 等；(6)直角都相等；(7)全等三角形对应角相等； (8)第三角代换，即等量代换等．
等，简记为A.S.A.(或角边角) 2. 证明书写格式：在△ABC和△A′B′C′中，
∠A＝∠A′， ∵ AB＝A′B′，
∠B＝∠B′， ∴△ABC≌△A′B′C′. 要点精析：(1)全等的元素：两角及两角夹边；(2)在书 写两个三角形全等的条件角边角时，一定要把夹边相等写 在中间，以突出角边角的位置以及对应关系．
总结
判定两三角形全等，先根据已知条件或求证的结论 确定三角形，然后再根据三角形全等的判定方法看缺什 么条件，再去证什么条件，简言之：即综合利用分析法 和综合法寻找证明途径．
思
考
全等三角形对应边上的中线、对应角的平分线 又有 什么关系呢？你能说明其中的道理吗？
全等三角形除了对应边相等、对应角相等外， 还有以下几条性质：
1.定理：两角分别相等且其中一角的对边相等的两个 三角形全等，简记为A.A.S.(或角角边)
证明书写格式：在△ABC和△A′B′C′中， ∠A＝∠A′，
∵ ∠B＝∠B′， BC＝B′C′，
∴△ABC≌△A′B′C′. 要点精析：(1)全等的元素：两角及其中一角的对边； (2)用S.A.S. ，A.S.A. ，A.A.S. 证明全等时，要注意图 形中隐含的相等的角．例如：对顶角、公共角、同角的余
图 13.2.9 把你画的三角形与其他同学画 的三角形 进行比较，或将你画的三

一、复习引入 你能列出下列代数式吗？ (1)两数和的平方；(2)两数差的平方． 你能计算出它们的结果吗？ 二、探究新知 你能发现它们的运算形式与结果有什么规律吗？ 引导学生用自己的语言叙述所发现的规律，允许学生之间 互相补充，教师不急于概括； 举例：(1)(p＋1)2＝(p＋1)(p＋1)＝________________； (2)(p－1)2＝(p－1)(p－1)＝________________； (3)(m＋2)2＝________________； (4)(m－2)2＝________________．
操作： (1)把画好的三角形剪下和原三角形重叠，观察能重合在 一起吗？ (2)上面的探究说明什么规律？ 总结：判定两个三角形全等的方法：两边和它们的夹角
分别相等的两个三角形全等，简写成“边角边”或
“SAS”．
三、举例分析
多媒体出示教材例2. 例2 如图，有一池塘，要测池塘两端A，B的距离，可先
在平地上取一个点 C， 从点 C 不经过池塘可以直接到达点 A
四、课堂练习 如图，已知AB＝AC，点D，E分别是AB和AC上的点， 且DB＝EC.求证：∠B＝∠C.
学生先独立思考，然后讨论交流，用规范的书写完成 证明过程．
五、小结与作业 1．师生小结：
(1)“边角边”判定两个三角形全等的方法．
(2)在判定两个三角形全等时，要注意使用公共边和公共 角． 2．布置作业：教材习题12.2第3，4题．
解：(1)(x＋2y－3)(x－2y＋3)
＝[x＋(2y－3)][x－(2y－3)] ＝x2－(2y－3)2
＝x2－(4y2－12y＋9)
＝x2－4y2＋12y－9；
(2)(a＋b＋c)2
＝[(a＋b)＋c]2 ＝(a＋b)2＋2(a＋b)c＋c2