下载文档原格式
量子物理量子力学原理与波粒二象性实验解析量子力学是研究微观世界的物理学理论，具有独特的原理和概念，并以其波粒二象性而闻名。
本文将深入探讨量子物理量子力学原理，并通过解析波粒二象性实验来阐明其基本原理。
一、量子力学的基本原理量子力学的基本原理主要包括波粒二象性、量子叠加原理、测不准原理和量子纠缠等。
其中，波粒二象性是量子力学的核心概念之一。
1. 波粒二象性波粒二象性指的是微观粒子既可以表现出粒子性质（如质量、位置等），又能表现出波动性质（如干涉、衍射等）。
这一概念的提出颠覆了经典物理学中对粒子和波的分别描述，揭示了微观世界的新奇特性。
2. 量子叠加原理量子叠加原理指出，当一个量子系统处于多个可能的状态时，它可以同时处于这些状态的叠加态，并且在测量之前不会确定其具体状态。
只有在测量时，量子系统才会坍缩到某个确定的状态，而测量结果的概率分布由波函数的模方给出。
3. 测不准原理测不准原理是量子力学的重要原理之一，它表明无法同时准确测量一对共轭变量（如位置和动量）的值。
这是由于测量过程必然会对量子系统产生干扰，从而导致测量结果的不确定性。
4. 量子纠缠量子纠缠是指两个或多个量子系统之间存在一种特殊的关系，它们的状态在微观层面上紧密相关，无论它们之间有多远的距离。
这种纠缠关系具有非局域性，违背了经典物理学的因果关系，被广泛应用于量子通信和量子计算领域。
二、波粒二象性实验解析波粒二象性实验是通过实验探索和验证量子力学的基本原理的重要手段之一。
下面将对几种经典的波粒二象性实验进行解析。
1. 双缝干涉实验双缝干涉实验是研究波粒二象性的经典实验之一。
它使用一个光源照射在一个屏幕上有两个小孔的障板，观察到光在屏幕上形成的干涉条纹。
当光被一个小孔射出时，表现出粒子性质，而当光通过两个小孔形成干涉条纹时，表现出波动性质。
这一实验结果直接证明了波粒二象性的存在。
2. 光电效应实验光电效应实验是用来研究光的粒子性质的经典实验之一。
高二物理《波粒二象性》知识点波粒二象性是量子力学的基要概念，是专门针对经典概念无法完整描述量子物体的物理行为而提出的假说。
以下是店铺为您整理的关于高二物理《波粒二象性》知识点总结的相关资料，希望对您有所帮助。
高二物理《波粒二象性》知识点总结一：黑体与黑体辐射1.热辐射(1)定义：我们周围的一切物体都在辐射电磁波，这种辐射与物体的温度有关，所以叫热辐射。
(2)特点：热辐射强度按波长的分布情况随物体的温度而有所不同。
2.黑体(1)定义：在热辐射的同时，物体表面还会吸收和反射外界射来的电磁波。
如果一些物体能够完全吸收投射到其表面的各种波长的电磁波而不发生反射，这种物体就是绝对黑体，简称黑体。
(2)黑体辐射特点：黑体辐射电磁波的强度按波长的分布只与黑体的温度有关。
注意：一般物体的热辐射除与温度有关外，还与材料的种类及表面状况有关。
二：黑体辐射的实验规律随着温度的升高，一方面，各种波长的辐射强度都有增加;另—方面，辐射强度的极大值向波长较短的方向移动。
三：能量子1.能量子：带电微粒辐射或吸收能量时，只能是辐射或吸收某个最小能量值的整数倍，这个不可再分的最小能量值E叫做能量子。
2.大小：E=hν。
其中ν是电磁波的频率，h称为普朗克常量，h=6.626x10—34J·s(—般h=6.63x10—34J·s)。
四：拓展：对热辐射的理解(1).在任何温度下，任何物体都会发射电磁波，并且其辐射强度按波长的分布情况随物体的温度而有所不同，这是热辐射的一种特性。
在室温下，大多数物体辐射不可见的红外光;但当物体被加热到5000C左右时，开始发出暗红色的可见光。
随着温度的不断上升，辉光逐渐亮起来，而且波长较短的辐射越来多，大约在1 5000C时变成明亮的白炽光。
这说明同一物体在一定温度下所辐射的能量在不同光谱区域的分布是不均匀的，而且温度越高光谱中与能量最大的辐射相对应的频率也越高。
(2).在一定温度下，不同物体所辐射的光谱成分有显著的不同。
量子物理学波粒二象性与不确定性原理量子物理学是研究微观领域中的物质和能量交互作用的学科。
它的出现颠覆了经典物理学的观念，引入了波粒二象性以及不确定性原理。
本文将介绍这两个重要的概念，并探讨它们对于物理学和我们对于世界的理解所产生的深远影响。
一、波粒二象性波粒二象性是指微观领域中粒子既可以表现出粒子性质，又可以表现出波动性质的特性。
根据波粒二象性理论，微观粒子，如电子、光子等，既可以表现出粒子特性，如位置的确定性和质量的存在，又可以表现出波动特性，如干涉和衍射等现象。
量子力学的波粒二象性得以实现的关键是波函数。
波函数描述了粒子在空间中的分布和运动状态，具有波动性质的粒子的波函数会表现为类似于波的特性，如频率、波长等。
而在测量时，波函数会崩塌为一个确定位置的粒子，表现出粒子性质。
波粒二象性给物理学带来了革命性的变化。
它解释了许多实验现象，如双缝干涉实验和光电效应，让我们对微观世界有了更深入的认识。
同时，波粒二象性也为实际应用提供了基础，如量子计算和量子通信等领域的发展。
二、不确定性原理不确定性原理是由维尔纳·海森堡于1927年提出的，它指出在对微观粒子进行测量时，无法同时准确获得其位置和动量的值，存在一定的不确定性。
这一原理揭示了测量对于微观粒子状态的干扰，以及粒子的本质具有固有的不确定性。
不确定性原理的数学表达是海森堡关系式，即Δx × Δp ≥ ħ/2，其中Δx表示位置不确定度，Δp表示动量不确定度，ħ为约化普朗克常数。
该关系式表明，位置和动量的不确定度成反比关系，无论做何种精确测量，这两个值的乘积都不能小于一定的最小值。
这一原理的重要性在于，不仅揭示了观测对粒子状态的影响，也限制了我们对粒子性质的认识。
我们无法同时准确得知粒子的位置和动量，只能通过概率分布来描述。
不确定性原理对于我们对世界的认识方式产生了深远的影响，引发了哲学上的思考和对于真实性的质疑。
不确定性原理的应用也是广泛的。
量子力学粒子的波粒二象性在量子力学中，粒子的波粒二象性是一个重要的概念。
根据这一理论，微观粒子既可以表现出波动性，也可以表现出粒子性。
这种现象的存在对于理解自然界的微观世界具有重要意义。
本文将探讨量子力学中粒子的波粒二象性，并介绍一些相关实验和应用。
首先，我们来了解一下波动性和粒子性的概念。
在经典物理学中，波动和粒子是互相排斥的概念。
例子如光学中的光波和银粒子。
在经典物理学的框架下，粒子性和波动性是不可兼得的。
然而，当我们深入研究微观世界时，量子力学的理论表明粒子和波动是互相关联的。
根据量子力学的波函数理论，微观粒子的状态可以用波函数（又称为量子态）来描述。
波函数包含了关于粒子位置、动量以及其他物理性质的信息。
当我们对粒子进行测量时，波函数会崩溃，得到的结果只可能是一种离散的、局部的状态。
这种崩溃的过程被称为波函数塌缩。
粒子的波动性可以通过一些实验来观察和验证。
例如，干涉实验就是一种常用的实验方法。
在干涉实验中，单个粒子被发射到一个光栅或者双缝装置中。
当粒子通过后，会形成干涉图样，表现出波动的性质。
这意味着粒子不仅仅是一个确定的位置，而是以概率分布的形式存在。
另外一个观察粒子波动性的实验是分子束实验。
在分子束实验中，气体分子以一束来传递，并通过狭缝进行定向。
当这些分子通过后，会在屏幕上形成干涉图案。
这说明分子也具有波动性，不仅仅是单个的粒子。
粒子的粒子性则可以通过测量粒子的位置和动量来观察和验证。
根据薛定谔方程，一个粒子的波函数可以被分解为几个不同的定态波函数的叠加。
每个定态波函数都对应一个确定的能量和动量。
当我们对粒子的位置进行测量时，就会得到一个确定的位置值，而无法得到其他位置信息。
然而，当我们对粒子的动量进行测量时，就会得到一个不确定的值。
这是由于波函数的不确定性原理所决定的。
根据这个原理，我们无法同时精确测量一个粒子的位置和动量。
粒子的粒子性就体现在这种测量不确定性上。
粒子的波粒二象性在实际应用中具有重要意义。
量子力学中的波粒二象性及其物理解释引言：量子力学是一门研究微观领域的物理学科，它描述了微观粒子的行为和性质。
在量子力学中，波粒二象性是一项重要的概念，它指出微观粒子既可以表现出波动性质，又可以表现出粒子性质。
本文将探讨波粒二象性的物理解释以及其在量子力学中的应用。
一、波粒二象性的物理解释波粒二象性的物理解释可以从波动和粒子两个方面来理解。
1. 波动性质的解释根据波动理论，波动是一种传播能量的方式。
在量子力学中，微观粒子也可以被视为一种波动，其波函数描述了粒子的状态和行为。
波函数的幅度和相位可以用来描述粒子的概率分布和干涉现象。
例如，双缝干涉实验中，电子通过两个狭缝时会产生干涉图样，这表明电子具有波动性质。
2. 粒子性质的解释粒子性质是指微观粒子具有局部性和离散性的特征。
根据粒子理论，微观粒子具有质量、电荷等物理量，并且可以与其他粒子发生碰撞。
例如，康普顿散射实验中，光子与电子发生碰撞，光子的能量和动量发生变化，这表明光子具有粒子性质。
二、波粒二象性的实验验证波粒二象性的存在可以通过一系列实验进行验证。
1. 双缝干涉实验双缝干涉实验是验证波粒二象性的经典实验之一。
在实验中，通过一个屏幕上的两个狭缝发射电子或光子，观察它们在另一个屏幕上产生的干涉图样。
如果将电子或光子视为粒子，那么它们应该在屏幕上形成两个亮斑。
但事实上，实验结果显示出干涉条纹，这表明电子和光子具有波动性质。
2. 康普顿散射实验康普顿散射实验是验证波粒二象性的另一个重要实验。
在实验中，通过发射X 射线束照射物体，观察X射线与物体中的电子发生散射后的能量变化。
根据经典物理学，光子应该与电子发生弹性碰撞，能量不会改变。
然而，实验结果显示出X 射线的能量发生了变化，这表明光子具有粒子性质。
三、波粒二象性在量子力学中的应用波粒二象性在量子力学中有广泛的应用，以下是其中几个例子：1. 波函数描述在量子力学中，波函数是描述微观粒子状态和行为的数学工具。
量子力学中的波粒二象性及其应用引言：量子力学是研究微观粒子行为的物理学分支，它揭示了微观粒子既具有波动性又具有粒子性的特性，这被称为波粒二象性。
本文将深入探讨量子力学中的波粒二象性及其应用。
一、波粒二象性的概念及实验研究量子力学中的波粒二象性是指微观粒子既具有波动性，表现为干涉和衍射等经典光学现象，又具有粒子性，表现为能量的离散分布和粒子位置的测量。
著名的双缝干涉实验证明了波粒二象性。
实验中，电子或光子通过双缝时，产生了干涉条纹，这表明微观粒子像波一样具有波动性；而当检测到电子或光子时，其位置呈现粒子性，只能出现在某一个点上。
二、波粒二象性的理论解释波粒二象性可以通过波函数的概念来解释。
根据量子力学的描述，物体的运动状态可以由波函数来描述。
波函数的模的平方表示了粒子在空间中的概率分布，与经典的粒子密度概念有所不同。
而波函数的相位则决定了波函数的波动性质。
三、波粒二象性及其应用1.微粒子的干涉和衍射根据波粒二象性的理论解释，微观粒子在通过狭缝时会产生干涉和衍射现象，这与光的干涉和衍射类似。
利用微粒子的干涉和衍射现象，我们可以研究微观粒子的性质，例如通过电子衍射可以测量晶体的结构，通过中子干涉可以进行材料表征和成像等。
2.量子纠缠和量子隐形传态波粒二象性也为量子纠缠和量子隐形传态提供了基础。
量子纠缠是指两个或多个微观粒子之间存在一种特殊的关联状态，其中一粒子的状态的测量结果会瞬间影响到另一粒子。
量子隐形传态是指通过特殊的操作，可以使得两个量子态之间的信息传递速度超过光速。
这些现象在量子通信和量子计算领域具有重要应用价值。
3.量子行走和量子力学模拟通过波粒二象性，我们可以在量子系统中进行类似于经典行走的操作，即量子行走。
量子行走可以模拟某些问题，如搜索、优化等，并在量子计算中发挥重要作用。
另外，波粒二象性还为量子力学模拟提供了工具，可以模拟其他物理系统，从而加深对复杂物理现象的理解。
4.波粒二象性与微观粒子的测量波粒二象性也对微观粒子的测量提出了挑战和限制。
量子物理19 世纪末，经典物理发展得相当成熟，人们认为对物理现象本质的认识已经完成。
开尔文勋爵曾说：物理学大厦已建成，后辈们修补就行了。
但晴朗的物理学天空中仍有“两朵乌云”：迈克耳孙—莫雷实验的“零结果”热辐射的“紫外灾难”这些矛盾迫使人们跳出经典物理学框架，去寻找新的解决途径。
20世纪的物理学由经典物理走向近代物理近代物理包括：▲相对论1905 狭义相对论、1916 广义相对论▲量子力学旧量子论1900 Planck 振子能量量子化1905 Einstein电磁辐射能量量子化1913 N.Bohr原子能量量子化∙量子力学的建立1924 德布罗意物质波假设1925 海森伯矩阵力学1926 薛定谔波动方程1927 戴维孙、汤姆孙电子衍射实验1928 狄拉克相对论波动方程∙量子力学的应用与发展量子力学：原子、分子、固体的结构与物性量子场论：核结构、基本粒子等第二十六章波粒二象性§26.1 黑体辐射△§26.2 光电效应§26.3 光子、光的二象性§26.4 康普顿散射§26.5 实物粒子的波动性§26.6 概率波与概率幅§26.7 不确定关系§26.1 黑体辐射一.热辐射物体受热会发光，即辐射电磁波：与温度有的电磁辐射，称为热辐射。
物体在任何温度下都会产生热辐射。
热辐射谱是连续谱：包含各种频率（波长）成份，且强度不同。
热辐射谱中的强度按频率（波长）的分布和物体温度有关：温度升高，短波成份增加激光、日光灯是热辐射吗？加热的铁块的颜色随温度的变化：无光→暗红→橙色→黄白→蓝白鸟羽毛的颜色是热辐射吗？维恩设计的黑体—小孔空腔二. 黑体黑体：能完全吸收各种频率或波长的电磁波而无反射的物体，即αν= 1 的物体。
黑体是理想化模型，即使是煤黑、黑珐琅对太阳光的吸收也小于99%。
电磁波射入后很难从小孔出来，小孔是黑体。
好的辐射体也是好的吸收体一个黑白花盘子的两张照片室温下的反射光1100K时自身辐射的光【演示】三. 黑体辐射谱（M ν~ ν关系）实验测量装置对黑体加热，会放出热辐射。
通过光栅的分光功能可得到黑体辐射频谱。
通过热电偶可得到黑体辐射的光谱辐出度。
黑体热电偶测M ν(T)光栅光谱仪T∙光栅可见光区黑体辐射和热辐射实验曲线太阳是黑体面积为M (T )钨丝辐射本领差νm= 5700K = 510nm，得T表面∙斯特藩—玻耳兹曼定律)( 4T T M σ=—斯特藩—玻耳兹曼常量428Kw/m 1067.5⋅⨯=-σ斯特藩—玻耳兹曼定律和维恩位移定律是测量高温、遥感、红外追踪等物理基础。
1879年，斯特藩实验上总结1884年，玻耳兹曼理论证明四. 经典物理学的困难黑体辐射的理论公式是什么？1900年，辐射的振子模型：空腔内的热辐射是电磁驻波∙维恩公式1896年，热力学理论+ 实验数据分析得到：T e T M /3)(βνναν-=（α，β为常量）高频段和实验符合，低频段明显偏离实验。
∙瑞利—金斯公式辐射的振子模型由经典电磁理论和能均分定理得到：即所谓的“物理学晴朗天空中的一朵乌云”ν/1014HzM ν[ 10-9 W/(m 2.Hz) ]瑞利－金斯公式实验值点维恩公式普朗克公式由经典理论导出的M ν(T ) ~ν公式都与实验曲线不完全符合五.普朗克的能量子假说和黑体辐射公式普朗克先用内差法后用其提出的能量子假设得到了黑体辐射公式：∙仍采用辐射的振子模型（简谐振子）∙能量子假设：简谐振子能量量子化频率为ν的简谐振子能量，只能是能量子ε=hν的整数倍：0，ε，2ε，...∙采用经典统计物理（玻耳兹曼分布）§26.3 光子、光的二象性一. 光子理论（1905年，爱因斯坦）▲电磁辐射由以光速c 运动的、局限在空间某一小范围内的光的能量子—光子组成光子能量ε= hν▲光子具有“整体性”∙光的发射、传播、吸收都是量子化的∙一束光就是以光速c 运动的一束光子流光强I = N⋅hν，N —光子数流通量波面被分割，光子并不被分割。
光子通过1 缝的概率正比于I1，1 2I1 I2双缝实验光子通过2 缝的概率正比于I2。
光子在某处出现的概率和该处光振幅的平方—光强成正比。
+1. 散射波中除原波长λ0 外，出现新波长λ，且λ> λ0—康普顿效应2. ∆λ= λ-λ0 随散射角ϕ增大而增大，和散射物质无关：o0=ϕo45=ϕo90=ϕo135=ϕMo, K αλI 0λ )cos 1(Δ C ϕλλ-=λC —电子康普顿波长实验值：λC = 0.0241Å二.康普顿效应的理论解释经典的电磁理论很难解释为何出现λ≠λ0 的散射，康普顿用光子理论做了成功的解释：▲X 射线光子与“静止”的“自由电子”进行弹性碰撞波长1Å 的X 射线的光子能量ε~104eV外层电子束缚能~ eV，室温下kT ~ 10-2eV▲碰撞过程中能量与动量守恒碰撞→电子获得能量→光子能量↓→散射X 射线频率↓或波长↑因为光子还可与石墨中被原子核束缚得很紧的内层电子发生碰撞。
1. 为何康普顿散射中存在原波长 0的散射？内层电子束缚能103 ~ 104eV，不能视为自由，而应视为与原子是一个整体。
所以这相当于光子和整个原子碰撞。
因为m原子>> m光子，所以在弹性碰撞中入射光子几乎不损失能量，即散射光子波长不变。
三. 讨论几个问题3. 为何在光电效应中不考虑动量守恒？在光电效应中，入射光是可见光或者紫外线，光子能量低，电子不能视为“自由”，故原子参与动量交换，光子—电子系统动量不守恒。
而原子质量较大，它参与的能量交换可忽略， 光子—电子系统能量仍可认为是守恒的。
4. 为何对可见光观察不到康普顿效应？因可见光光子能量不够大，原子内的电子不能视为自由，故可见光不能产生康普顿效应。
四.康普顿散射实验的意义▲支持了“光量子”概念，进一步证实了：ε= hν▲首次实验证实了爱因斯坦提出的“光量子具有动量”的假设：p = ε/c = hν/c = h /λ▲证实了在微观领域的单个碰撞事件中，动量和能量守恒定律仍然成立。
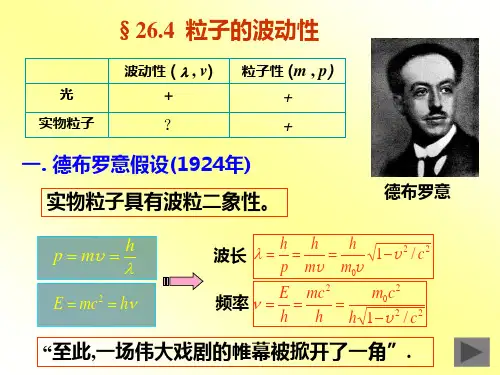
五. 吴有训的研究贡献散射角ϕ= 120ºλ0= 5.62nm证实了康普顿效应的普遍性，以及两种散射机制：λ—外层电子（自由电子）散射λ0—内层电子（整个原子）散射▲汤姆孙（G. P. Thomson ）实验（1927）1929 年德布罗意获诺贝尔物理奖，1937 年戴维孙、汤姆孙共获诺贝尔物理奖。
衍射图象电子通过金的多晶薄膜的衍射实验：实验原理图金多晶薄膜电子束衍射图象电子衍射【演示】▲约恩孙（Jonsson ）实验（1961）电子的单、双、三、四缝衍射实验：其它微观粒子如质子、中子…也有波动性。
单缝双缝三缝四缝§26.6 概率波与概率幅一.物质波的本质德布罗意：是引导粒子运动的“导波”。
—本质不明确薛定谔：波是基本的，电子是“波包”。
—波包不稳定，而电子是稳定的另一观点：粒子是基本的，电子的物质波是大量电子间相互作用形成的。
—被下面实验否定电子一个一个依次入射双缝的衍射实验700003000200007个电子100个电子底片上出现一个个点子说明：电子具有粒子性。
电子一个个入射，增多后形成衍射图样说明：单个电子就具有波动性，干涉是电子“自己和自己”的干涉，干涉不是电子间相互作用的结果。
单个电子在空间某处（如屏幕上某点）出现是概率性的，在一定条件下（如双缝）其概率是有确定规律的（如衍射花样所体现的）。
玻恩（M. Born ）对物质波的诠释：德布罗意波并不像经典波那样代表真实的物理量的波动，而是描述粒子在空间概率分布的“概率波”。
二.波函数假设及其统计解释概率波波函数：量子力学基本假设之一：微观粒子的状态用波函数描述复函数（值是复数）),(t r Ψ 波函数又称：态函数、态矢量、态…玻恩对波函数的统计诠释（1926）：∙模方称为“概率密度”2|),(|t r Ψ ∙波函数是描述粒子空间概率分布的“概率幅”),(t r Ψ 表示：在t 时刻，一个粒子出现在位置处的单位体积中的概率。
r 2|),(|t r Ψ t 时刻出现在d V 内的概率：Vt r Ψd |),(|2 d Vx y zr量子力学的不同于经典的波函数：它无直接的物理意义，不可以直接测量；有意义的是，可以直接测量。
),( t r Ψ 2|),(|t r Ψ 统计解释对波函数的要求—标准条件∙有限性在空间任何有限体积元∆V 中，粒子出现的概率必须为有限值：⎰⎰⎰V V ΨΔ2d || 有限。
