下载文档原格式
2-5 求通过(0)1x =，(1)2x =，使下列性能泛函为极值的极值曲线*()x t ：2(1)ft t J x dt =+⎰解：由题可知，始端和终端均固定被积函数21L x =+，0L x ∂=∂，2L x x ∂=∂， 2d L x dt x∂⋅=∂ 代入欧拉方程0L d L x dt x∂∂-⋅=∂∂，可得20x =，即0x = 故1x c = 其通解为：12x c t c =+代入边界条件(0)1x =，(1)2x =，求出11c =，21c = 极值曲线为*()1x t t =+2-6 已知状态的初值和终值为(1)4x =，()4f x t =式中f t 自由且f t >1，试求使下列性能泛函达到极小值的极值轨线*()x t ：211[2()()]2ft J x t x t dt =+⎰ 解：由题可知，2122L x x =+，()4f t ψ=，()14x =，()4f x t = 欧拉方程：L 0d L x dt x∂∂-=∂∂ 横截条件：()00t x =x ，()()f f x t t ψ=，()0fTt L L x x ψ∂⎛⎫+-= ⎪∂⎝⎭易得到2dxdt= 故12x t c =+ 其通解为：()212x t t c t c =++根据横截条件可得：()()()122121114424f f f f f x c c x t t c t c x t t c ⎧=++=⎪⎪=++=⎨⎪=+=⎪⎩解以上方程组得：12569f t c c =⎧⎪=-⎨⎪=⎩将f t ，1c ，2c 代入J 可得5*201500502150233J x x dt =+=-=⎰ 极值轨线为()*269x t t t =-+2-7 设性能泛函为120(1)J x dt =+⎰求在边界条件(0)0x =，(1)x 自由情况下，使性能泛函取极值的极值轨线*()x t 。
解：由题可知，21L x =+，()00x =，()1x 自由欧拉方程：L 0d L x dt x∂∂-=∂∂ 横截条件：()00t x =x ，L 0ft x∂=∂，0fTt L L x x ∂⎛⎫+= ⎪∂⎝⎭易得到()x t a =其通解为：()x t at b =+代入边界条件()f x t a =，()00x =，1f t =，求出0a =，0b = 将f t ，a ，b 代入J 可得()1*211J x dt =+=⎰极值轨线为()*0x t = 2-9 求使泛函22211220(2)J x x x x dt π=++⎰为极值并满足边界条件1(0)0x =，2(0)0x =1()12x π=，2()12x π=- 的极值轨线*1()x t 和*2()x t 。
2-5 求通过(0)1x =，(1)2x =，使下列性能泛函为极值的极值曲线*()x t ：2(1)ft t J x dt =+⎰解：由题可知，始端和终端均固定被积函数21L x =+,0L x ∂=∂，2L x x ∂=∂， 2d Lx dt x ∂⋅=∂代入欧拉方程0L d Lx dt x ∂∂-⋅=∂∂,可得20x =，即0x =故1x c = 其通解为：12x c t c =+代入边界条件(0)1x =，(1)2x =，求出11c =，21c = 极值曲线为*()1x t t =+2-6 已知状态的初值和终值为(1)4x =，()4f x t =式中f t 自由且f t 〉1，试求使下列性能泛函达到极小值的极值轨线*()x t ：211[2()()]2ft J x t x t dt =+⎰ 解：由题可知，2122L x x =+，()4f t ψ=，()14x =,()4f x t = 欧拉方程：L 0d Lx dt x ∂∂-=∂∂横截条件：()00t x =x ，()()f f x t t ψ=，()0fT t L L x x ψ∂⎛⎫+-= ⎪∂⎝⎭易得到2dxdt= 故12x t c =+ 其通解为:()212x t t c t c =++根据横截条件可得：()()()122121114424f f f f f x c c x t t c t c x t t c ⎧=++=⎪⎪=++=⎨⎪=+=⎪⎩解以上方程组得：12569f t c c =⎧⎪=-⎨⎪=⎩将f t ,1c ,2c 代入J 可得5*201500502150233J x x dt =+=-=⎰ 极值轨线为()*269x t t t =-+2-7 设性能泛函为120(1)J x dt =+⎰求在边界条件(0)0x =，(1)x 自由情况下,使性能泛函取极值的极值轨线*()x t 。
解：由题可知，21L x =+，()00x =，()1x 自由欧拉方程：L 0d L x dt x∂∂-=∂∂ 横截条件:()00t x =x ，L 0ft x∂=∂，0fT t L L x x ∂⎛⎫+= ⎪∂⎝⎭易得到()x t a =其通解为：()x t at b =+代入边界条件()f x t a =，()00x =，1f t =，求出0a =,0b = 将f t ，a ,b 代入J 可得()1*2011J x dt =+=⎰极值轨线为()*0x t = 2-9 求使泛函22211220(2)J x x x x dt π=++⎰为极值并满足边界条件1(0)0x =，2(0)0x =1()12x π=，2()12x π=- 的极值轨线*1()x t 和*2()x t 。
2-5 求通过(0)1x =，(1)2x =，使下列性能泛函为极值的极值曲线*()x t ：2(1)ft t J x dt =+⎰解：由题可知，始端和终端均固定，被积函数21L x =+，0L x ∂=∂，2L x x ∂=∂， 2d L x dt x∂⋅=∂ 代入欧拉方程0L d Lx dt x∂∂-⋅=∂∂，可得20x =，即0x =故1x c = 其通解为：12x c t c =+代入边界条件(0)1x =，(1)2x =，求出11c =，21c = 极值曲线为*()1x t t =+2-6 已知状态的初值和终值为(1)4x =，()4f x t =式中f t 自由且f t >1，试求使下列性能泛函达到极小值的极值轨线*()x t ：211[2()()]2ft J x t x t dt =+⎰ 解：由题可知，2122L x x =+，()4f t ψ=，()14x =，()4f x t = 欧拉方程：L 0d L x dt x∂∂-=∂∂ 横截条件：()00t x =x ，()()f f x t t ψ=，()0fTt L L xx ψ∂⎛⎫+-= ⎪∂⎝⎭易得到2dxdt= 故12x t c =+ 其通解为：()212x t t c t c =++根据横截条件可得：()()()122121114424f f f f f x c c x t t c t c x t t c ⎧=++=⎪⎪=++=⎨⎪=+=⎪⎩解以上方程组得：12569f t c c =⎧⎪=-⎨⎪=⎩ 还有一组解⎪⎩⎪⎨⎧===12121c c t f (舍去，不符合题意f t >1)将f t ，1c ，2c 代入J 可得3140)3(4)212(5025.2*=-=+=⎰⎰•t dt x x J . 极值轨线为()*269x t t t =-+2-7 设性能泛函为120(1)J x dt =+⎰求在边界条件(0)0x =，(1)x 自由情况下，使性能泛函取极值的极值轨线*()x t 。
最优控制课后习题答案最优控制课后习题答案最优控制是现代控制理论中的重要分支，它研究如何在给定约束条件下，使系统的性能指标达到最优。
在最优控制的学习过程中，课后习题是巩固理论知识、培养解决问题能力的重要环节。
本文将为大家提供一些最优控制课后习题的答案，希望能对大家的学习有所帮助。
1. 线性二次型最优控制问题考虑一个线性时不变系统，其状态方程和性能指标分别为：$$\begin{align*}\dot{x}(t) &= Ax(t) + Bu(t) \\J(u) &= \int_{0}^{T} (x^T(t)Qx(t) + u^T(t)Ru(t))dt\end{align*}$$其中，$x(t)$为系统的状态向量，$u(t)$为控制输入向量，$A$和$B$为系统矩阵，$Q$和$R$为正定矩阵，$T$为最优控制的时间段。
求解该问题的最优控制输入$u^*(t)$。
答案：根据最优控制的原理，最优控制输入$u^*(t)$满足以下的最优性条件：$$\begin{align*}\frac{\partial J}{\partial u}(u^*(t)) &= 2R u^*(t) + 2B^T P(t)x(t) = 0 \\\dot{P}(t) &= -PA - A^T P - Q + PBR^{-1}B^T P\end{align*}$$其中，$P(t)$为状态向量的共轭变量矩阵。
通过求解上述的代数方程和微分方程，可以得到最优控制输入$u^*(t)$和状态向量的共轭变量矩阵$P(t)$。
2. 非线性最优控制问题考虑一个非线性系统，其状态方程和性能指标分别为：$$\begin{align*}\dot{x}(t) &= f(x(t), u(t)) \\J(u) &= \int_{0}^{T} g(x(t), u(t)) dt\end{align*}$$其中，$f(x(t), u(t))$为非线性函数，$g(x(t), u(t))$为性能指标函数。
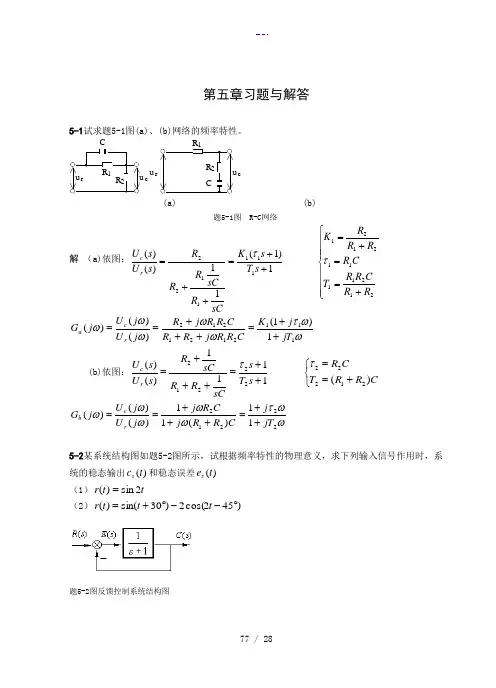
第五章习题与解答5-1试求题5-1图(a)、(b)网络的频率特性。
u rR1u cR2CR2R1u r u c(a) (b)题5-1图 R-C网络解（a)依图：⎪⎪⎪⎩⎪⎪⎪⎨⎧+==+=++=++=2121111212111111221)1(11)()(RRCRRTCRRRRKsTsKsCRsCRRRsUsUrcττωωτωωωωω11121212121)1()()()(jTjKCRRjRRCRRjRjUjUjGrca++=+++==(b)依图：⎩⎨⎧+==++=+++=CRRTCRsTssCRRsCRsUsUrc)(1111)()(2122222212ττωωτωωωωω2221211)(11)()()(jTjCRRjCRjjUjUjGrcb++=+++==5-2某系统结构图如题5-2图所示，试根据频率特性的物理意义，求下列输入信号作用时，系统的稳态输出)(tcs和稳态误差)(tes（1）ttr2sin)(=（2）)452cos(2)30sin()(︒--︒+=tttr题5-2图反馈控制系统结构图解 系统闭环传递函数为: 21)(+=Φs s 频率特性: 2244221)(ωωωωω+-++=+=Φj j j 幅频特性: 241)(ωω+=Φj相频特性: )2arctan()(ωωϕ-=系统误差传递函数: ,21)(11)(++=+=Φs s s G s e 则)2arctan(arctan )(,41)(22ωωωϕωωω-=++=Φj j e e（1）当t t r 2sin )(=时,2=ω，r m =1则,35.081)(2==Φ=ωωj 45)22arctan()2(-=-=j ϕ4.1862arctan )2(,79.085)(2====Φ=j j e e ϕωω )452sin(35.0)2sin()2( -=-Φ=t t j r c m ss ϕ)4.182sin(79.0)2sin()2( +=-Φ=t t j r e e e m ss ϕ （2）当)452cos(2)30sin()(︒--︒+=t t t r 时: ⎩⎨⎧====2,21,12211m m r r ωω5.26)21arctan()1(45.055)1(-=-===Φj j ϕ 4.18)31arctan()1(63.0510)1(====Φj j e e ϕ)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t c m m ss ϕϕ+-⋅Φ-++⋅Φ= )902cos(7.0)4.3sin(4.0 --+=t t)]2(452cos[)2()]1(30sin[)1()(j t j r j t j r t e e e m e e m ss ϕϕ+-⋅Φ-++⋅Φ=)6.262cos(58.1)4.48sin(63.0 --+=t t5-3若系统单位阶跃响应h t e e t t t()..=-+≥--11808049试求系统频率特性。
1. 已知二阶系统的状态方程122()(),()()x t x t x t u t ==性能泛函3222221212120111[(3)2(3)][2()4()2()()()]222J x x x t x t x t x t u t dt =+++++⎰求最优控制。
解:把状态方程和性能指标与标准状态方程和标准性能指标比较，可得0,101,02,11,,,,0,010,21,42A B P Q R ⎡⎤⎡⎤⎡⎤⎡⎤=====⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦考虑到()K t 是对称阵，设11121222,(),k k K t k k ⎡⎤=⎢⎥⎣⎦代入黎卡提方程1()()()()()()()()()()()T T K t K t A t A t K t K t B t R t B t K t Q t -=--+-即1112111211121112111212221222122212221222,,,,,0,10,002,12[0,1],0,01,0,,1,1,4,k k k k k k k k k k k k k k k k k k k k ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=--+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦令上式等号左右端的对应元相等，得211121211122222212222221224k k k k k k k k k =-=-+-=-+-这是一组非线性微分方程。
由边界条件(3)K P =即11121222(3),(3)1,0(3),(3)0,2k k k k ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ 最优控制为11112112122212222()()(),()2*[0,1]2()2(),()T u t R B K t X t k k x t k x t k x t k k x t -=-⎡⎤⎡⎤=-=--⎢⎥⎢⎥⎣⎦⎣⎦2. 能控的系统状态方程为122()(),()()x t x t x t u t ==这是一种双积分系统，其输出为1()x t ，其输入为()u t ，其传递函数为12()1()()x s G s u s s==其性能泛函为222112201[()2()()()()]2J x t bx t x t ax t u t dt ∞=+++⎰其中220a b ->求最优控制。
1. ·2.已知二阶系统的状态方程122()(),()()x t x t x t u t ==性能泛函3222221212120111[(3)2(3)][2()4()2()()()]222J x x x t x t x t x t u t dt =+++++⎰求最优控制。
解:把状态方程和性能指标与标准状态方程和标准性能指标比较，可得0,101,02,11,,,,0,010,21,42A B P Q R ⎡⎤⎡⎤⎡⎤⎡⎤=====⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦考虑到()K t 是对称阵，设11121222,(),k k K t k k ⎡⎤=⎢⎥⎣⎦代入黎卡提方程1()()()()()()()()()()()T T K t K t A t A t K t K t B t R t B t K t Q t -=--+-即1112111211121112111212221222122212221222,,,,,0,10,002,12[0,1],0,01,0,,1,1,4,k k k k k k k k k k k k k k k k k k k k ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=--+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦令上式等号左右端的对应元相等，得211121211122222212222221224k k k k k k k k k =-=-+-=-+-这是一组非线性微分方程。
由边界条件(3)K P =即11121222(3),(3)1,0(3),(3)0,2k k k k ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ 最优控制为11112112122212222()()(),()2*[0,1]2()2(),()T u t R B K t X t k k x t k x t k x t k k x t -=-⎡⎤⎡⎤=-=--⎢⎥⎢⎥⎣⎦⎣⎦3. ）4.能控的系统状态方程为122()(),()()x t x t x t u t ==这是一种双积分系统，其输出为1()x t ，其输入为()u t ，其传递函数为12()1()()x s G s u s s==其性能泛函为222112201[()2()()()()]2J x t bx t x t ax t u t dt ∞=+++⎰其中220a b ->求最优控制。
解：稳态时连续系统的状态调节器问题：由状态方程和性能指标求得0,101,,,10,01A B Q R ⎡⎤⎡⎤⎡⎤====⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦b ，b,a 显然Q 为半正定阵。
可控性阵为[]0,1,1,0B AB ⎡⎤=⎢⎥⎣⎦是非奇异的，系统可控。
考虑到()K t 是对称阵，设11121222(),K t k k =⎢⎥⎣⎦代入黎卡提方程1()()()()()()()()()()()T T K t K t A t A t K t K t B t R t B t K t Q t -=--+-即1112111211121112111212221222122212221222,,,,,0,10,001,[0,1],0,01,0,,1,,,k k k k k k k k k k b k k k k k k k k b a k k ⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=--+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦令上式等号左右端的对应元相等，得2111212122211222221212k k k k k k b k k k a=-=--=--当111222f t →∞时，k 、k 、k 都趋于零，则黎卡提微分方程变为黎卡提代数方程2121222112221201002k k k k b k k a=-=--=--上面的方程组可得111222k 、k 、k 的稳态值111222 =1 b k k k 为保证K 正定，根据塞尔韦斯特判据，K 的各阶主子式应大于零，即 *211221122120,0,k k k k k >>>将求得的111222k k k 、、的值代入上面正定性条件，可得1+a >最优控制可计算如下1111211212222()()(),()[0,1]()(),()T u t R B K t X t k k x t x t t k k x t -=-⎡⎤⎡⎤=-=-⎢⎥⎢⎥⎣⎦⎣⎦由于12()1()()x s G s u s s==拉氏反变换得1()x t ut =2()()1u t x t t=-+ 5. 22211210min (0.1),,J x u dt x x u x x ∞=+=-+=⎰求最优控制。
解：稳态时连续系统的状态调节器问题：由状态方程和性能指标求得1,010,0,,0.11,00A B Q R -⎡⎤⎡⎤⎡⎤====⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦，0,1显然Q 为半正定阵。
可控性阵为[]1,1,0,1B AB -⎡⎤=⎢⎥⎣⎦是非奇异的，系统可控。
%考虑到()K t 是对称阵，设11121222(),K t k k =⎢⎥⎣⎦代入黎卡提方程1()()()()()()()()()()()T T K t K t A t A t K t K t B t R t B t K t Q t -=--+-即1112111211121112111212221222122212221222,,,,,1,01,110,010[1,0],1,00,0,,0,,k k k k k k k k k k k k k k k k k k k k ⎡⎤--⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤=--+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦0,1令上式等号左右端的对应元相等，得211111212121122122221210210101k k k k k k k k k k =-=-+=-当111222f t →∞时，k 、k 、k 都趋于零，则黎卡提微分方程变为黎卡提代数方程211121211221221201020100101k k k k k k k =-=-+=-上面的方程组可得111222k 、k 、k 的稳态值111222=1 1k k k为保证K 正定，根据塞尔韦斯特判据，K 的各阶主子式应大于零，即211221122120,0,k k k k k >>>将求得的111222k k k 、、的值代入上面正定性条件，满足。
最优控制可计算如下11112111112212222()()(),()10[1,0]10()10(),()T u t R B K t X t k k x t k x t k x t k k x t -=-⎡⎤⎡⎤=-=--⎢⎥⎢⎥⎣⎦⎣⎦6. 线性系统的状态方程()(),(0)1x t u t x =-=性能泛函220(()())J x t u t dt ∞=+⎰试求最优控制函数。
解：0,1,2,2a b q r ==-==[因为()()x t u t =-，系统是可控的。
黎卡提代数方程10Ka aK Kb bK q r--+-=代入得1202KK -=解得20K => 最优控制1()()u t bKx t r =-代入得11()()*2()()2u t bKx t x t x t r =-==代入状态方程：()()x t x t =-所以tx ce -= 又因为(0)1x =所以1c =所以最优控制()tu t e -= 7. 22210min (),k k k k k k J xu x x u +==+=+∑试求最优控制函数。
解：本题为离散状态调节器问题。
由题意：1,1,0,1,1,3A B P Q R N ====== 黎卡提方程可写为111()()()[(1)()()()]()T T K k Q k A k K k B k R k B k A k ---=+++。
代入得11(1)()1[(1)1]1(1)1K k K k K k K k --+=+++=+++终端值(3)(3)0K P ==。
由3k =反向计算，求出(2)(1)(0)K K K 、、。
(3)(2)1=1(3)1K K K =++，(2)3(1)=1=(2)12K K K ++，(1)8(0)1=(1)15K K K =++最优控制1()()()()[()()]()T T u k R k B k A k K k Q k X k --=--代入得()[()1]()u k K k X k =--3(0)[(0)1](0)(0)5u K x x =--=-，2(1)(0)(0)(0)5x x u x =+=再计算(1)u11(1)(1)(0)25u x x =-=-，1(2)(1)(1)(0)5x x u x =+=再计算(2)u(2)[(2)1](2)0u K x =--=8. 给定一阶系统()(),(1)3,x t u t x ==性能泛函62201(5)()2J x u t dt =+⎰试求最优控制*,u 使J 取极小值。
(解：由题意得：0A =，1B =，2P =，0Q =，1R =黎卡提方程可写为1()()()()()()()()()()()TTK t K t A t A t K t K t B t R t B t K t Q t -=--+- 代入得2()()K t K t =解得：1()K t t c =-+又因为()2f K t P ==所以132c =-则12()131322K t t t =-=-- 最优控制计算如下2()()()()132u t K t X t X t t=-=--代入状态方程2()()()132x t u t x t t ==--解得()(213)x t c t =-又因为(1)3x =所以311c =-639()11t x t -+=9. 对一维线性系统1220(1)()2(),0,1,..., 1.()4(),()N k x k x k u k k N J x N u k ββ-=+=+=-=+∑为正常数求使J 取最小值的最优控制。
解：由题意：()1,()2,2,0,8A k B k P Q R β=====黎卡提方程可写为111()()()[(1)()()()]()T T K k Q k A k K k B k R k B k A k ---=+++ 代入得111(1)()[(1)]212(1)K k K k K k K k ββ--+=++=++ *1()()()()[()()(1)()]()(1)()TTU k L k X k L k R k B k K k B k B k K k A k -=-=+++()L k 最优反馈增益阵代入11(1)()()()[84(1)]2(1)()*()22(1)K k U k L k X k K k K k X k X k K k ββ-+=-=-+++=-++10. 921(),..(1)()(),(0)1,(10)02J u k s t x k x k u k x x α=+=+==∑求最优控制*()u k 和 最优轨迹*()x k 。
