伯努利实验

伯努利定理概率论伯努利定理是概率论中的一项重要定理，它描述了在随机试验中，某个事件发生的概率与其对立事件不发生的概率之间的关系。

本文将从概率论的角度对伯努利定理进行详细解析。

一、伯努利试验的概念伯努利试验是指满足以下条件的随机试验：1. 试验只有两个可能结果，分别记为事件A和事件A的对立事件非A；2. 每次试验的结果相互独立，即前一次试验的结果不会影响后一次试验的结果；3. 每次试验中事件A发生的概率为p，非A发生的概率为1-p。

二、伯努利定理的表述根据伯努利试验的定义，我们可以得到伯努利定理的表述：在n次独立重复进行的伯努利试验中，事件A发生k次的概率为：P(X=k) = C(n,k) * p^k * (1-p)^(n-k)其中，C(n,k)表示从n个元素中选取k个元素的组合数。

三、伯努利定理的应用伯努利定理在概率论和统计学中有着广泛的应用，下面列举几个常见的应用场景。

1. 二项分布当伯努利试验重复进行n次时，事件A发生k次的概率符合二项分布。

二项分布可以用来描述多次重复试验中事件发生次数的概率分布。

2. 投硬币问题将一枚硬币抛掷n次，每次出现正面的概率为p。

根据伯努利定理，我们可以计算出在n次抛掷中，出现k次正面的概率。

3. 赌博问题在赌博中，常常需要计算在多轮游戏中获胜的概率。

如果每轮游戏中获胜的概率为p，那么根据伯努利定理，我们可以计算出在n轮游戏中获胜k次的概率。

四、伯努利定理的意义伯努利定理是概率论中的基础定理之一，它揭示了随机试验中事件发生的规律。

通过应用伯努利定理，我们可以计算出各种概率问题的解答，帮助我们更好地理解和分析概率事件。

除了伯努利定理，还有一些与之相关的概率定理，如大数定律和中心极限定理。

大数定律指出，当试验次数足够多时，事件发生的频率会趋近于事件发生的概率。

中心极限定理则指出，当试验次数足够多时，多次试验结果的平均值将近似服从正态分布。

伯努利定理是概率论中的重要定理，它描述了在伯努利试验中事件发生的概率与其对立事件不发生的概率之间的关系。

返回
数据处理
▪ 实验报告须验证伯努利方程及静力学方程
返回
a、Hf(1-A) 点1~点A压头损失=v为零时点A测压管液柱高度-某测定 流量下测压管A的冲压头液柱高度
b、Hf(1-B) 点1~点B压头损失=v为零时点B测压管液柱高度-某测定 流量下测压管B的冲压头液柱高度
c、Hf(1-C) 点1~点C压头损失=v为零时点C测压管液柱高度-某测定 流量下测压管C的冲压头液柱高度
返回
实验步骤
▪ 1、调节出水阀门至一定开度。 ▪ 2、待液流稳定，且检查稳压水槽的恒定
水位后，测读柏努利方程实验管三个截面 三组测压管的液柱高度。可以重复测读三 次，合理选择稳定的读数或取其三次的平 均值，以提高测试的准确度。 ▪ 3、测定此工作状况下的液流流量。
返回
实验步骤
▪ 4、改变出水阀门的开度，在新工作状况下 重复上述测试。
2. 开启进水阀向稳压水槽注水，或开关试验导 管出口调节阀时，一定要缓慢地调节开启程 度，并随时注意设备内的变化。
3. 试验过程中需根据测压管量程范围，确定最 小和最大流量。
4. 为了便于观察测压管的液柱高度，可在临实 验测定前，向各测压管滴入几滴红墨水。
返回
数据处理
1.压头损失的计算
总压头=450mm水柱
▪ 以单位质量流体为衡算基准
gH1
v12 2
p1
gH2
v22 2
p2
hf
(1)
▪ 以单位重量流体为衡算基准
H1
v12 2g
p1
g
H2
v22 2g
p2
g
Hf
(2)
返回
实验原理
▪ 不可压缩流体的机械能衡算方程，可根据以下 情况进行简化：

推论
设在一次试验中，事件A首次发生的概率为p(0<p<1)，则在伯努利试验序列中，事件A在第 k次试验中才首 次发生的概率为。
特殊情形
二项分布
几何分布
二项分布
一般地，在n次独立重复试验中，ξ表示事件A发生的次数。如果事件A发生的概率是p，则不发生的概率 q=1-p，n次独立重复试验中，事件A发生k次的概率是：P(ξ=k)= (k=0,1,2,3…n），那么就说ξ服从参数p的二 项分布，其中p称为成功概率。记作：ξ~B(n,p)。
（1）几何分布的期望Eξ= ； （2）几何分布的方差Dξ=。
谢谢观看
单个伯努利试验是没有多大意义的，然而，当我们反复进行伯努利试验，去观察这些试验有多少是成功的， 多少是失败的，事情就变得有意义了，这些累计记录包含了很多潜在的非常有用的信息。
试验要点
试验要点
重复试验的相互独立性
伯努利试验是在同样的条件下重复地、相互独立地进行的一种随机试验，其中“在相同条件下”意在说明： 每一次试验的结果不会受其它实验结果的影响，事件之间相互独立。
多次试验
判断某种试验是否为伯努利试验的关键是：首先，必须是重复的试验，即多次试验，而非一次试验；其次， 每次试验的结果同其他各次试验的结果无关，即事件发
典例
（1）连续的n次射击； （2）连续的掷n次硬币。
相关定理
设在一次试验中，事件A发生的概率为p（0<p<1），则在n重伯努利试验中，事件A恰好发生 k次的概率 为：。
介绍
介绍
伯努利试验是一个有两种结果的简单试验，它的结果是成功或失败，黑或白，开或关，没有中间的立场，没 有妥协的余地。这样的例子也特别多，例如我们观察从一副纸牌中拿出一张牌，它或者是黑色或者是红色；接生 一个婴儿，或者是男孩或者是女孩；我们经历24小时的一天，或者遇到流星或者遇不到流星。在每一种情况下， 很方便设计一种结果“成功”，另外一种结果为“失败”，例如选出一张黑色牌，生出一个女儿，没有遇到流星 都可以表示为“成功”。然而，从概率的角度看，选择红牌、儿子、遇到流星为成功也是不会产生差异的。在这 种场合下，“成功”是没有价值取向的色彩。

伯努利方程实验实验一 伯努利方程实验一、实验目的观察流体在管道中流动时能量的相互转化现象，加深对柏努利方程的理解。

原理二、实验原理流体在流动时，具有3种机械能：位能、静压能和动能，这3种机械能是可以相互转化的。

在没有摩擦损失的自流管路中，任意两截面处的机械能总和是相等的。

在有摩擦损失的自流管路中，任意两截面处的总机械能之差为摩擦损失。

2．对理想流体，在系统中任一截面处，尽管三种机械能彼此不一定相等，但这三种机械能的总和是不变的。

对于实际流体，由于在内摩擦，流体在流动过程中总有一部分机械能随摩擦转化为热能而损耗了，故对于实际流体，任意两截面上的机械能的总和并不相等，两者的差值即为能量损失。

3流体流经管路某截面处的各种机械能大小均可以用测压管中的一 段液柱高度来表示，在流体力学中，用以表示各种机械能大小的流体柱高度称之为“压头’。

分别称为位压头、动压头、静压头、损失压头。

机械能可用测压管中液柱的高度来表示。

当测压管口平行于流动方向时，液柱的高度表示静压能；当测压管口正对流体流动方向时，液柱的高度表示动能与静压能之和，两者之差就是动能。

实验中通过测定流体在不同管径、不同位置测压管中液面高度，反映出摩擦损失的存在及动能、静压能之间的相互转化。

（4）流体的机械能衡算，以单位质量（1kg ）流体为衡算基准，当流体在两截面之间稳定流动且无外功加入时，伯努利方程的表达形式为 式中 z —— 位压头（m 流体柱）； —— 静压头（m 流体柱）； —— 动压头（m 流体柱）。

三、实验设备及流程Cgvg p z =++22ρg Pρ22v1. 实验装置流程如图3-1所示，实验设备由玻璃管、测压管、活动测压头、水槽、循环水泵等组成。

水槽中的水通过循环水泵将水送到高位槽，并由溢流口保持一定水位，然后流经玻璃管中的各测点，再通过出口阀A流回水箱，由此利用循环水在管路中流动观察流体流动时发生能量转化及产生能量损失。

活动测压头的小管端部封闭，管身开有小孔，小孔位置与玻璃管中心线平齐，小管又与测压管相通，转动活动测压头就可以测量动、静压头。

伯努利试验公式
伯努利试验公式是描述管道或管道中流体流动的基本物理定律之一。

其公式表示为：
P + 1/2ρv^2 + ρgh = 常数
其中，P为流体静压力，ρ为流体密度，v为流体流速，g为重力加速度，h为流体高度。

这个公式说明了在管道或管道中，流体静压力、动能和位能之和是一个常数。

换句话说，当流速增加时，静压力会下降，而动能和位能则会增加，以保持总能量不变。

这个公式在航空、汽车、液压和水力工程等领域中都得到了广泛应用。

例如，它可以用来计算飞机、汽车或船只的速度、液压系统的压力、水力发电厂的效率等等。

需要注意的是，伯努利试验公式只适用于稳态流动的情况，即流体的速度和压力分布不随时间变化。

在非稳态流动或湍流中，该公式的适用性可能会受到限制。

虑带有反射壁及弹性壁的随机游动等类型.
当 p = q = 1 时，随机游动称为是对称的，这时质点向 右或向左的概2 率是一样的. 这里只介绍两种最简单的随机
游动模型.
无限制的随机游动
假定质点在时刻0从原点出发，以 Sn表示它在时刻 t = n时的
位置. 为了使质点在时刻 t = n 时位于 y( k也可以是负整数 )，当且仅当在前 n 次游动中向右游动的次数（记为 x）比 向左游动的次数（记为 y）多 k 次.故有
以 f (k; r, p) 记其概率.
Ck 发生当且仅当前面的k-1 次试验中有 r -1 次出现成功， k - r 次失败，而在第 k 次试验的结果是成功，这两个事件的
概率分别为
C p q r−1 r−1 k −r k −1
和
p
利用试验的独立性得
f
(k;
r,
p)
=
Cr−1 k−1
pr−1qk−r
(2)事件A 在每次试验中出现的概率 p 保持不变.
(3)各次试验相互独立,
(4)共进行n次试验.
n 重伯努利试验的基本结果可以记作
ω = (ω1,ω2,",ωn )
其中 ω i 或者为A,或者为 A .这样的 ω 共有 2 n 个，这
2n 个样本点组成了样本空间 Ω .
设样本点 ω = (ω1 , ω2 ," , ω n ) 中有 k 个A ，n- k 个
并称出现 A 为“成功”，A 为“失败”.
这种只有两个结果的试验称为伯努利试验.
在伯努利试验中，首先要给出下面的概率：
P( A) = p, P( A) = q = 1− p. 其中： p ≥ 0, q ≥ 0, p + q = 1.

伯努利试验的公式伯努利试验，这可是个在概率学里相当重要的概念呢！咱先来说说伯努利试验到底是啥。

简单来讲，伯努利试验就是一种只有两种可能结果的试验，比如抛硬币，正面或者反面；投篮，进或者不进。

这两种结果我们通常称为“成功”和“失败”。

伯努利试验的公式是：P(X=k) = C(n, k) * p^k * (1 - p)^(n - k) 。

这里面的字母都代表着特定的意思，n 表示试验的次数，k 是成功的次数，p 是每次试验成功的概率。

比如说，咱假设投篮成功的概率是 0.6，要进行 5 次投篮，想知道恰好成功 3 次的概率。

那咱就可以用这个公式来算算。

C(5, 3)就是从 5 次里选 3 次成功的组合数，这得用组合的公式去算。

算出来再乘以 0.6 的 3 次方，再乘以 0.4 的 2 次方，就能得出恰好成功3 次的概率啦。

我想起之前给学生们讲这个公式的时候，有个小同学特别有意思。

当时我在黑板上写了一道例题，问大家：“如果一个抽奖活动，中奖概率是 0.2，抽 10 次，恰好中奖 2 次的概率是多少？”大家都开始埋头算，这时候有个小同学突然举手说：“老师，我觉得这抽奖不靠谱，概率这么低，还不如去买糖吃。

”全班同学都笑了。

不过笑归笑，大家还是认真地用公式算出了答案。

这个公式在实际生活中的应用可多了去了。

比如说产品质量检测，一批产品里次品出现的概率；或者是疾病传播，一个人在一定时间内感染某种疾病的概率等等。

再比如，有个工厂生产灯泡，知道次品率是 0.05，随机抽检 20 个灯泡，想知道有 1 个次品的概率，这时候伯努利试验的公式就能派上用场啦。

总之，伯努利试验的公式虽然看起来有点复杂，但只要理解了其中的原理，多做几道题练练手，就会发现它其实也没那么难。

而且学会了这个公式，能帮助我们解决好多实际问题，让我们对生活中的各种不确定性有更清晰的认识和把握。

希望大家都能把这个公式掌握好，在概率的世界里畅游无阻！。

伯努利试验概念： 是在同样的条件下重复地、各 次之间相互独立地进行的一种试验。
伯努利试验特征： 这种试验中，每一次试验只有 两种结果，即某事件A要么发生，要么不发生。并 且每次发生的概率都是相同的。
如何判断伯努利试验： 判断是否为独立重复试验的关 键是每次试验事件A的概率不变，并且每次试验的结果 同其他各次试验的结果无关，重复是指试验为一系列的 试验，并非一次试验，而是多次，但要注意重复事件发 生的概率相互之间没有影响。
奎屯
以上面的公式恰为[(1 p) p]n 展开式中的第 k 1 项，可见排列
组合、二项式定理及概率间存在着密切的联系 新疆 王新敞 奎屯
在 n 次独立重复试验中， 记 Ai 是“第 i 次试验的结果” 显然， P( A1 A2 An ) = P( A1 )P( A2 )
P( An )
∵“相同条件下”等价于各次试验的结果不会受其 他试验的影响, ∴独上立面重等 复试式验成的立特. 点：
1）每次试验只有两种结果，要么发生，要么不发 生；
学习小结:
1．独立重复试验模型要从三方面考虑 第一：每次试验是在同 新疆 王新敞 奎屯
样条件下进行 第二：各次试验中的事件是相互独立的 第三，每次
新疆
新疆
王新敞
王新敞
奎屯
奎屯
试验都只有两种结果，即事件要么发生，要么不发生 新疆 王新敞 奎屯 2．如果 1 次试验中事件 A 发生的概率是 p ，那么 n 次独立重
复试验中这个事件恰好发生 k
次的概率为
Pn (k )
Cnk
pk (1
p)nk
新疆 王新敞
奎屯
对于此式可以这么理解：由于 1 次试验中事件 A 要么发生，要么

实验二 伯努利实验一、实验目的流动流体所具有的总能量是由各种形式的能量所组成，并且各种形式的能量之间又相互转换。

当流量在导管内作定常流动时，在导管的各截面之间的各种形式机械能的变化规律，可由机械能衡算基本方程来表达。

这些规律对于解决流体流动过程的管路计算、流体压强、流速与流量的测量，以及流体输送等问题，都有着十分重要的作用。

本实验采用一种称之为伯努利试验仪的简单装置，实验观察不可压缩流体在导管内流动时的各种形式机械能的相互转化现象并验证机械能衡算方程（伯努利方程）。

通过实验加深对流体流动过程基本原理的理解。

二、实验原理l 、不可压缩的流体在导管中作稳定流动，系统与环境又无功的交换，若以单位质量流体为衡算基准，其机械能守恒方程式为：∑+++=++fhp u g z p u g z ρρ2222121122（1）式中，u l 、u 2 ——分别为液体管道上游的某截面和下游某截面处的流速，m·s -1；P 1、P 2 ——分别为流体在管道上游截面和下游截面处的压强，Pa ；z l 、z 2 ——分别为流体在管道上游截面和下游截面中心至基准水平的垂直距离，m ； ρ ——流体密度，Kg·m -3；∑h f ——流体两截面之间消耗的能量，J·Kg -1。

若以单位重量为衡算基准，机械能守恒方程式又可以表达为：∑+++=++fHgp gu z gp gu z ρρ2222121122 m 液柱（2）式中，z l 、z 2 ——液体的位压头，m 液柱；∑H f ——流动系统内因阻力造成的压头损失，m 液柱。

2、理想流体在管内稳定流动，若无外加能量和损失，则可得到：ρρ2222121122p u g z p u g z ++=++（3）式（3）表示1kg 理想流体在各截面上所具有的总机械能相等，但各截面上每一种形式的机械能并不一定相等，但各种形式的机械能之和为常数，能量可以相互转换。

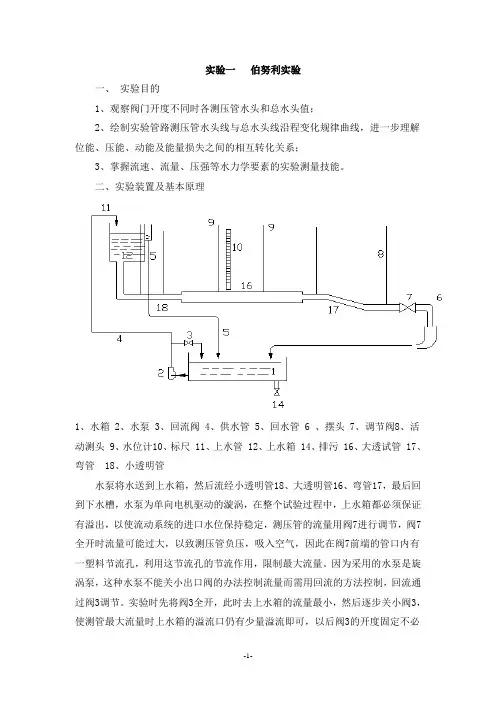
实验一伯努利实验一、实验目的1、观察阀门开度不同时各测压管水头和总水头值；2、绘制实验管路测压管水头线与总水头线沿程变化规律曲线，进一步理解位能、压能、动能及能量损失之间的相互转化关系；3、掌握流速、流量、压强等水力学要素的实验测量技能。

二、实验装置及基本原理1、水箱2、水泵3、回流阀4、供水管5、回水管 6 、摆头 7、调节阀8、活动测头 9、水位计10、标尺 11、上水管 12、上水箱 14、排污 16、大透试管 17、弯管 18、小透明管水泵将水送到上水箱，然后流经小透明管18、大透明管16、弯管17，最后回到下水槽，水泵为单向电机驱动的漩涡，在整个试验过程中，上水箱都必须保证有溢出，以使流动系统的进口水位保持稳定，测压管的流量用阀7进行调节，阀7全开时流量可能过大，以致测压管负压，吸入空气，因此在阀7前端的管口内有一塑料节流孔，利用这节流孔的节流作用，限制最大流量。

因为采用的水泵是旋涡泵，这种水泵不能关小出口阀的办法控制流量而需用回流的方法控制，回流通过阀3调节。

实验时先将阀3全开，此时去上水箱的流量最小，然后逐步关小阀3，使测管最大流量时上水箱的溢流口仍有少量溢流即可，以后阀3的开度固定不必每次都调节。

测压管各点上的压强，有活动测头8、水位计9测量，活动测头有一小管伸入透明测管内，小管末端封闭，而管身上钻有一个小测压孔，该孔处于透明测压管的中心线上，试验时，当小孔正对水流方向时，测得的是总压；而垂直水流方向测得的是测压管水头。

测压管的流量通过活动摆头6用体积法进行测量。

三、实验步骤1、实验前的准备（1）检查零流速时，各水位记高度是否一致，如不一致，可能是测管内有汽泡或者安装高度不一致，应采取相应措施进行处理。

（2）合上水泵电源开关，如水泵不动，应即停电检查。

（3）检查当阀7全开时，上水箱是否仍有溢出，如无溢出，应适当关小阀3。

（4）检查摆头是否灵活。

2、实验进行（1）首先记录调节阀全关时的水位，即零流量水位及实验水温。

P( A1A2 An ) P( A1)P( A2 A1)P( A3 ( A1A2 )) P( An ( A1 A2 An1))
全概率公式
设Ａ1 ，Ａ2 ，...，Ａn 构成一个完备事件组，且 Ｐ(Ａi )＞0 ，i＝1，2，...，n，则对任一随机事件Ｂ， 有
n
P(B) P( Ai )P(B | Ai ) i 1
C42 p2q42 6 0.052 0.952 0.0135
伯努利定理
定理
设在一次试验中事件Ａ发生的概率为 p (0<p<1) ， 则Ａ在n次伯努里试验中恰好发生 k次的概率为
Pn
(k)

CLeabharlann k npkqnk
其中 q 1 p
( k＝ 0，1，2，...，n )
例 有一批棉花种子,其出苗率为0.67,现每穴种4粒种子,
(1) 求恰有ｋ粒出苗的概率(0≤k≤4)； (2) 求至少有两粒出苗的概率．
解 (1) 该试验为4 重伯努利试验
n 4, p 0.67, q 1 p 0.33
P4(k) C4k pk q4k (0 k 4)
(2) 设Ｂ表示至少有2粒出苗的事件,则
P(B) P4 (2) P4 (3) P4 (4) 0.8918
例 设某人打靶，命中率为0.7，重复射击5次，求恰好 命中3次的概率。
解 该试验为5重伯努利试验，且 n=5,p=0.7;q=0.3;k=3
所求概率为
P( A) C53 0.73 0.32 0.3087
例 设某电子元件的使用寿命在1000小时以上的概 率为0.2，当三个电子元件相互独立使用时，求在使 用了1000小时的时候，最多只有一个损坏的概率。

Company LOGO
伯努利方程验证实验 及装置改进
小组成员： 指导老师：龙天渝
目录
1. 前言 2.实验原理 3.实验装置和方法 4.实验数据及分析 5.总结
一、前 言
❖ 伯努利方程采用能量守恒定律解决了流体的流动问题，明 确了动能和势能、流速和压强相互转换的普遍规律，是流 体力学中最基本、最重要的方程。
四.实验数据及分析
❖ 图5中的测压管水头线和总水头 线，线性规整、直观，很好地 表达了恒定总流中各能量的变 化关系。
❖ 总水头线总是沿程减少，这是 由于沿程总有能量损失，这个 损失包括沿程损失和局部损失:
❖ 沿程损失随着长度的增加而增 加，而局部损失是突然增加的， 因此，在实验管道的B,C点总水 头线急剧减少。
❖ 由表1可知，在理想恒定元流伯努利方程验证实验管中①一 ③测点的总水头相对误差在5%以内，从而验证了恒定元流伯 努利方程的正确性.
四.实验数据及分析
四.实验数据及分析
❖ 本实验中，恒定总流伯努利方程验证实验管道中测点(1)-(7)的测压管读数见 表2。根据表2中的第1组的测压管水头和总水头数据，可绘制出恒定总流伯努 利方程验证实验管道长度方向上A-E的测压管水头线和总水头线变化趋势。
，ｂ处速度
增加，压强减少，称为静压。由于毕托管比较细小，只是微弱的
改变原来的流场，且ａ与ｂ 间相距很短，可近似认为ｂ处压强
就是ａ处的静压，ａ、ｂ位于同一条流线上（元流上），此
时，测压管ｂ′的测定值为
。
二、实验原理
二、实验原理
❖ 变径实验管道
❖ 建立如图３所示的变径实验管道，连接处用突扩管（Ｂ处）
❖ 但是目前普遍采用的不可压缩流体恒定伯努利方程验证实 验及实验仪最突出的问题是没有将理想恒定元流伯努利方 程和实际恒定总流伯努利方程加以区分，将理想恒定流和 实际恒定流混为一谈，不利于学生对伯努利方程基本原理 的理解。

P( Bk ) P( ) Cnk p k q nk
Bk
事件A在n次试验中发生k次的概率为
Pn (k ) Cnk p k q nk
0 k n
这个概率常称为二项概率，记为 bk ; n, p
k k nk pq 即： b(k；n, p) Cn
k=0，1，2，…，n
解：50千瓦电力可用时供给5台机床开动，因而10台机床中 同时开动的台数为不超过5台时都可以正常工作，而每 台机床只有“开动”与“不开动”的两种情况，且开动 的概率为12/60=1/5。不开动的概率为4/5。设10台机床 k 1 k 4 10 k 中正在开动着的机床台数为 ，则 P ( k ) C10 ( ) ( ) 0 k 10
1699年，雅各布当选为巴黎科学院外籍院士；1701年被柏林 科学协会（后为柏林科学院）接纳为会员。 许多数学成果与雅各布的名字相联系。例如悬链线问题 （1690年），曲率半径公式（1694年），“伯努利双纽线” （1694年），“伯努利微分方程”（1695年），“等周问题” （1700年）等。 雅各布对数学最重大的贡献是在概率论研究方面。他从1685 年起发表关于赌博游戏中输赢次数问题的论文，后来写成巨著 《推测术》，这本书在他死后8年，即1713年才得以出版。 最为人们津津乐道的轶事之一，是雅各布醉心于研究对数螺 线，这项研究从1691年就开始了。他发现，对数螺线经过各种变 换后仍然是对数螺线，如它的渐屈线和渐伸线是对数螺线，自极 点至切线的垂足的轨迹，以极点为发光点经对数螺线反射后得到 的反射线，以及与所有这些反射线相切的曲线（回光线）都是对 数螺线。他惊叹这种曲线的神奇，竟在遗嘱里要求后人将对数螺 线刻在自己的墓碑上，并附以颂词“纵然变化，依然故我”，用 以象征死后永

柏努利实验一、实验目的l 、研究流体各种形式能量之间关系及转换，加深对能量转化概念的理解;2、深入了解柏努利方程的意义。

二、实验原理l 、不可压缩的实验液体在导管中作稳定流动时，其机械能守恒方程式为：∑+++=+++fe h p u g z W p u g z ρρ2222121122 （1）式中：u l 、u 2一分别为液体管道上游的某截面和下游某截面处的流速，m ／s ；P 1、P 2一分别为流体在管道上游截面和下游截面处的压强，Pa ；z l 、z 2一分别为流体在管道上游截面和下游截面中心至基准水平的垂直距离，m;ρ一流体密度，Kg ／m ； We —液体两截面之间获得的能量，J ／Kg;g 一重力加速度，m ／s 2； ∑h f 一流体两截面之间消耗的能量，J ／Kg 。

2、理想流体在管内稳定流动，若无外加能量和损失，则可得到：ρρ2222121122p u g z p u g z ++=++ （2）表示1kg 理想流体在各截面上所具有的总机械能相等，但各截面上每一种形式的机械能并不一定相等，但各种形式的机械能之和为常数，能量可以相互转换。

3、 流体静止，此时得到静力学方程式：ρρ2211p g z p g z +=+（3）所以流体静止状态仅为流动状态一种特殊形式。

三、实验装置及流程试验前，先关闭试验导管出口调节阀，并将水灌满流水糟，然后开启调节阀，水由进水管送入流水槽，流经水平安装的试验导管后，试验导管排出水和溢流出来的水直接排入下水道。

流体流量由试验导管出口阀控制。

进水管调节阀控制溢流水槽内的溢流量，以保持槽内液面稳定，保证流动系统在整个试验过程中维持稳定流动。

d=30mm d=18mm图1柏努利实验装置图四、实验内容（一）演示1、静止流体的机械能分布及转换将试验导管出口阀全部关闭，以便于观察（也可在测压管内滴入几滴红墨水），观察A、B、C、D点处测压管内液柱高低。

2、一定流量下流体的机械能分布及转换缓慢调节进水管调节阀，调节流量使溢流水槽中有足够的水溢出，再缓慢慢开启试验导管出口调节阀，使导管内水流动（注意出口调节阀的开度，在实验中能始终保持溢流水槽中有水溢出），当观察到试验导管中部的两支测压水柱略有差异时，将流量固定不变，当各测压管的水柱高度稳定不变时，说明导管内流动状态稳定。

设“发出信号.”为事件A，“接收信号.”为B 则
P ( A ) 0 . 6 ; P ( A ) 0 . 4 ; P ( B A ) 0 . 8 ; P ( B A ) 0 . 2 ; P ( B A ) 0 . 9 ; P ( B A ) 0 . 1
2， 在一盒子中装有15个乒乓球，其中有9个新球。 在第一次比赛时任意取出三个球，比赛后仍放回原 盒中；在第二次比赛时同样任意取出三个球，求第 二次取出的三个球均为新球的概率。
A A A A , A A A A , A A A A 1234 1234 1234
因为Ａ1，Ａ2，Ａ3，Ａ4 相互独立，所以
C 6
2 4
P ( A A A A ) P ( A ) P () A P () A P () A 1 2 3 4 1 2 3 4
0 . 05 0 . 95 p q
3 9 3 1 5
3 6 3 1 5
21 96 3 1 5
3 7 3 1 5
12 96 3 1 5
3 8 3 1 5
3 6 3 1 5
3 9 3 1 5
某工人照看三台机床，一个小时内1号，2号，3号 机床需要照看的概率分别为0.3, 0.2, 0.1。设各机床之 间是否需要照看是相互独立的，求在一小时内：1）没 有一台机床需要照看的概率；2）至少有一台不需要照 看的概率；3）至多有一台需要照看的概率。
P 4 ( k ) C p q
(2)
k k 4 k 4
(0k 4 )
设Ｂ表示至少有2粒出苗的事件,则
P ( B ) P ( 2 ) P ( 3 ) P ( 4 ) 4 4 4 0 . 8 9 1 8
例 设某人打靶，命中率为0.7，重复射击5次，求恰好

三重伯努利试验公式
三重伯努利试验公式是指在一次试验中，进行了三次伯努利试验的情况下，得到事件发生次数的概率公式。

假设进行三次伯努利试验，每次试验的结果只有两种可能，分别记为事件发生（记为S）和事件不发生（记为F）。

记第一次、第二次和第三次试验事件发生的概率分别为p，q，r。

根据伯努利试验的定义，每次试验的结果都是相互独立的。

因此，三次试验的结果可以看作是一个三元组（X,Y,Z），其中
X表示第一次试验结果，Y表示第二次试验结果，Z表示第三
次试验结果。

根据概率论的乘法原理，事件（X=k，Y=l，Z=m）的概率可
以表示为：
P(X=k, Y=l, Z=m) = p^k * q^l * r^m
其中k，l，m都是0或1。

为了求得事件发生次数的概率，我们需要考虑所有可能的情况。

事件发生次数为0的概率为：
P(0次) = P(X=0, Y=0, Z=0) = q^3
事件发生次数为1的概率为：
P(1次) = P(X=1, Y=0, Z=0) + P(X=0, Y=1, Z=0) + P(X=0, Y=0,
Z=1) = 3pqr
事件发生次数为2的概率为：
P(2次) = P(X=1, Y=1, Z=0) + P(X=1, Y=0, Z=1) + P(X=0, Y=1, Z=1) = 3p^2qr + 3pq^2r + 3pqr^2
事件发生次数为3的概率为：
P(3次) = P(X=1, Y=1, Z=1) = p^3
根据以上公式，我们可以计算事件发生次数的概率。

伯努利实验特征伯努利实验又称二维卡方检验，是衡量实验组与对照组在某个或某些变量上是否存在显著性差异的一种统计检验方法。

它是用来验证在6个或更多个变量中观测到的可能结果各种分布频率与常识上可预期的频率是否相符，因其检验方法统计领域著名统计学家R.A.Fisher在1920年代率先提出而得名。

伯努利实验可以用于检验超过二分类的变量，也可以用于检验某个统计指标，比如检验两批样本的均值是否有差异，以及检测连续变量的分布情况是否存在显著差异。

伯努利实验最主要的特点就是实验组与对照组的观察结果有正项亦有反项，分别是观察结果发生／未发生。

伯努利实验所提出的假设就是检验实验组与对照组在某测量指标上之间存在显著性差异的假说，即实验组与对照组的结果的发生概率不相等。

要想检验这个假说，需要先根据实验结果，生成一个2×2的联合概率分布，以频数表的形式汇总实验的观察数据并计算出联合分布的频率数，接着根据实验结果比较计算出的频率数与理论可能发生的频率数，采用卡方检验思想，判断实验结果是否与理论结果存在显著性差异。

伯努利实验的优势之一在于检验试验的可靠度比较高，虽然它不能用于非完全抽样的实验，但也可以把半完全抽样作为抽样方法，用其他抽样方法采集实验结果，把这些抽取的数据作为伯努利实验的样本，这样就可以获得较高的实验结果的准确度。

此外，对于调查对象的数量量也不需很大，若调查对象数量较少，仍可以看出结果的显著性差异。

此外，伯努利实验的使用还没有要求实验中所有参与者只有“成功”和“失败”两种可能结果，而是可以根据实验中所涉及到的多个变量，将成功与失败分为多种结果，例如偏好取决于所选择的产品种类，那么可以以“偏爱A”、“不偏爱A”、“偏爱B”、“不偏爱B”、“偏爱C”及“不偏爱C”的多种可能结果来定义抽样组在偏好度上的分类情况。

而伯努利实验有一个主要缺点，就是在实验中涉及多个变量时，因为每个变量都有着多种可能结果，因此在计算联合概率分布时数据量较大，容易出现混淆，也就是说，当变量数较多时，伯努利实验可能会出现无法求解的情况，因此，试验者不能太过依赖伯努利实验，它仅能作为参考，而不能用来作为多重假设的全面性检验。