下载文档原格式
三角函数的图像和性质1、用五点法作正弦函数和余弦函数的简图（描点法）：正弦函数y=sinx ，x ∈[0，2π]的图象中，五个关键点是：(0,0) (2π,1) (π,0) (23π,-1) (2π,0) 余弦函数y=cosx x ∈[0,2π]的图像中，五个关键点是：(0,1) (2π,0) (π,-1) (23π,0) (2π,1) 2 sin y x = cos y x = tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值 当22x k ππ=+时，max 1y =；当22x k ππ=- 时，min 1y =-．当2x k π=时，max 1y =；当2x k ππ=+时，min1y =-．既无最大值也无最小值周期性 2π 2ππ奇偶性奇函数 偶函数 奇函数单调性 在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦上是增函数； 在32,222k k ππππ⎡⎤++⎢⎥⎣⎦上是减函数． 在[]2,2k k πππ-上是增函数； 在[]2,2k k πππ+上是减函数．在,22k k ππππ⎛⎫-+⎪⎝⎭上是增函数．对称性 对称中心(),0k π 对称轴2x k ππ=+对称中心,02k ππ⎛⎫+ ⎪⎝⎭对称轴x k π=对称中心,02k π⎛⎫⎪⎝⎭无对称轴函数 性质例作下列函数的简图(1)y=|sinx|，x ∈[0，2π]， (2)y=-cosx ，x ∈[0，2π]例利用正弦函数和余弦函数的图象，求满足下列条件的x 的集合：21sin )1(≥x 21cos )2(≤x3、周期函数定义：对于函数()y f x =，如果存在一个非零常数T ，使得当x 取定义域内的每一个值时，都有：()()f x T f x +=，那么函数()y f x =就叫做周期函数，非零常数T 叫做这个函数的周期。
注意： 周期T 往往是多值的（如sin y x = 2π,4π,…,-2π,-4π,…都是周期）周期T 中最小的正数叫做()y f x =的最小正周期（有些周期函数没有最小正周期）sin y x =, cos y x =的最小正周期为2π （一般称为周期）正弦函数、余弦函数：ωπ=2T 。
正切、余切函数的图象和性质正切、余切函数的图象和性质张思明教学目的：〔略〕教学过程择录：一、引题：师：比照上一节的习题，请同学们看一看自己的作业本，对正弦和余弦函数，在作业中，我们已涉及了多少类型的问题？生众：P159〔11〕正弦，余弦函数的定义域：P158〔3〕正弦，余弦函数的最值〔值域〕：P158〔6〕正弦，余弦函数的奇偶性P159〔8〕正弦，余弦函数的单调性P159〔7〕正弦，余弦函数的应用一-----比大小P158〔4〕正弦，余弦函数的周期〔最小正周期〕P159〔12〕正弦，余弦函数的图象P160〔16、17〕正弦，余弦函数性质的应用教师在黑板上书写：〔1〕定义域〔2〕值域〔3〕奇偶性〔4〕单调性〔5〕比大小〔6〕求最小正周期〔7〕作图〔8〕应用教师：今天我们来学习正切、余切函数的图象和性质，可以想一想，我们要觖决什么问题？生众：不就是上面这几点问题吗？教师：说的不错，我们就是要来解决把“正弦、余弦函数〞换成“正切、余切函数〞后〔1〕~〔7〕后面加一个“是什么？〞这样一些问题。
请同学们带的这些问题看书5分钟〔P153~P157〕。
[评述]：这里是通过作业小结的方式引入问题。
学生常常是很肓目的做作业，很少观察作业所涉及的问题类型和范围。
教师有意识地引导学生作这种观察，既培养了学生看课本的习惯，又自然引出了今天的课题和要探索解决的问题。
二、学生自己回忆性设问，〔自问自答〕5分钟以后：学生阅读完毕，教师指导第一组学生〔7人〕为相邻的同桌的同学〔第二组学生〕就前面七个方向提一个有关正、余切函数性质的问题，要求是后面的同学不要提前面已经提到过的问题，并请同桌同学〔起立〕对着大家答复。
做完后，问、答的两组学生角色交换。
其它组的同学一边听，一边作判断，对的放过，不对时请同一行的同学予以更正：生1：正切函数的定义域是什么？邻生答：除了，k∈Z外的全体实数。
生2：正切函数的值域是整个y轴吗？邻生改正：应说成是全体实数生3：………生10：学过四种三角函数都是奇数吗？都是增函数吗？邻生答：不对，反例是余弦函数〕生11：正切函数是它定义域上的增函数吗？〔好问题！〕邻生答：是，其它学生更正：不是。
三角函数的正切与余切关系解析三角函数是数学中重要的概念之一，其中正切和余切是相互关联的两个函数。
在本文中，我们将详细解析正切和余切的关系及其相关性质。
一、正切与余切的定义正切函数（tangent function）和余切函数（cotangent function）是三角函数中的两个重要函数。
在单位圆上，这两个函数与正弦和余弦函数之间存在一定的关系。
正切函数定义如下：tan(x) = sin(x) / cos(x)余切函数定义如下：cot(x) = 1 / tan(x) = cos(x) / sin(x)其中，x为角度值或弧度值，sin(x)代表正弦函数值，cos(x)代表余弦函数值。
二、正切与余切的性质1. 定义域和值域：正切函数和余切函数的定义域为x ≠ (2k + 1)π/2 (k为整数)，即除去所有以π/2为倍数的点。
正切函数的值域为R，即所有实数。
余切函数的值域也为R，即所有实数。
2. 奇偶性：正切函数是奇函数，即tan(-x) = -tan(x)。
余切函数是奇函数，即cot(-x) = -cot(x)。
3. 周期性：正切函数和余切函数的周期都是π，即tan(x + π) = tan(x)，cot(x + π) = cot(x)。
4. 正切和余切的关系：由正弦和余弦函数定义可得，tan(x) = sin(x) / cos(x)，cot(x) = cos(x) / sin(x)。
这意味着正切和余切是正弦和余弦的倒数关系。
5. 正切和余切的图像：正切函数和余切函数的图像都是无界的，并且在定义域内具有周期性。
三、正切与余切的应用正切与余切在数学和科学中有广泛的应用，以下是其中一些重要应用：1. 三角方程的求解：在解三角方程时，正切和余切的性质可以用来简化等式，从而求解方程。
2. 函数图像的分析：正切和余切函数的图像特点可以用于分析函数的性质，如最值、增减性、极值点等。
3. 三角恒等式的证明：在证明三角恒等式时，正切和余切的关系可以用来推导等式的两边，从而证明恒等式的成立。
精锐教育学科教师辅导讲义讲义编号_学员编号： 年 级：高一 课 时 数：3 学员姓名： 辅导科目：数学 学科教师：课 题 正、余切函数的图像和性质授课日期及时段教学目的熟练掌握正、余切函数的图像及其性质（单调性、奇偶性、周期性）；能灵活利用他们的性质解题。
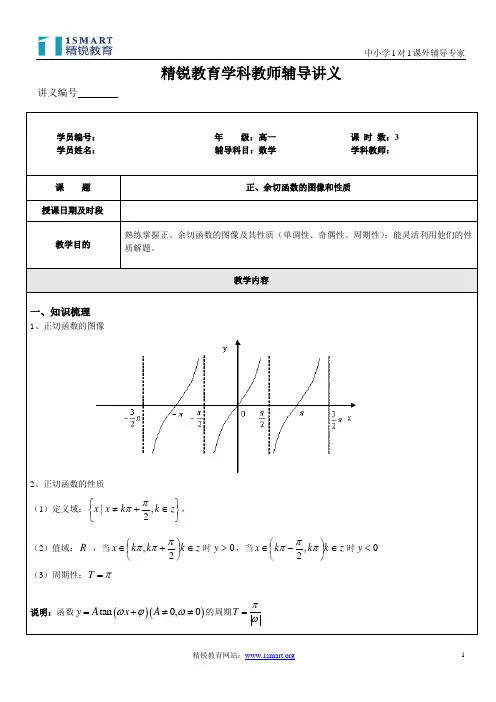
教学内容一、知识梳理1、正切函数的图像2、正切函数的性质 （1）定义域：⎭⎬⎫⎩⎨⎧∈+≠z k k x x ,2|ππ， （2）值域：R ，当z k k k x ∈⎪⎭⎫⎝⎛+∈2,πππ时0>y ，当z k k k x ∈⎪⎭⎫⎝⎛-∈πππ,2时0<y（3）周期性：π=T说明：函数()()tan 0,0y A x A ωϕω=+≠≠的周期T πω=求三角函数式的最小正周期时，要尽可能地化为只含一个三角函数，且三角函数的次数为1的形式，否则很容易出现错误。
（4）奇偶性：()x x tan tan -=-奇函数，对称中心是,02k π⎛⎫⎪⎝⎭()k Z ∈ 特别提醒：正(余)切型函数的对称中心有两类：一类是图像与x 轴的交点，另一类是渐近线与x 轴的交点，但无对称轴，这是与正弦、余弦函数的不同之处。
（5）单调性：在开区间z k k k ∈⎪⎭⎫⎝⎛+-2,2ππππ内，函数单调递增。
但要注意在整个定义域上不具有单调性。
余切函数的图像和性质：二、例题解析例1 函数y ＝x tan log 21的定义域是( )A ｛x ｜0＜x ≤4π） B ｛x ｜2k π＜x ≤2k π＋4π，k ∈Z }C ｛x ｜k π＜x ≤k π＋4π，k ∈Z }D ｛x ｜k π－2π＜x ≤k π＋4π，k ∈Z }巩固训练1、函数1tan y x =-的定义域是_______2、函数)1(cot log 2-x 的定义域是________2、函数tan 2()tan xf x x=的定义域为（ ） A ．{|x x R ∈ 且,4k x k Z π⎫≠∈⎬⎭B ．{|x x R ∈ 且,2x k k Z ππ⎫≠+∈⎬⎭C ．{|x x R ∈ 且,4x k k Z ππ⎫≠+∈⎬⎭D ．{|x x R ∈ 且,4k x k k Z ππ⎫≠-∈⎬⎭4、函数tan()4y x π=-的定义域是（ ）A ．|,4x x x R π⎧⎫≠∈⎨⎬⎩⎭ B ．|,4x x x R π⎧⎫≠-∈⎨⎬⎩⎭C ．|,,4x x k k R x R ππ⎧⎫≠+∈∈⎨⎬⎩⎭ D ．3|,,4x x k k Z x R ππ⎧⎫≠+∈∈⎨⎬⎩⎭例2 函数tan()(0)6y ax a π=+≠的周期为（ ）.A ．2a π B ．2aπ C ．a π D ．a π 例3 比较大小：（1）125tan 与137tan ； （2）⎪⎭⎫ ⎝⎛-34tan π与⎪⎭⎫⎝⎛-511tan π。
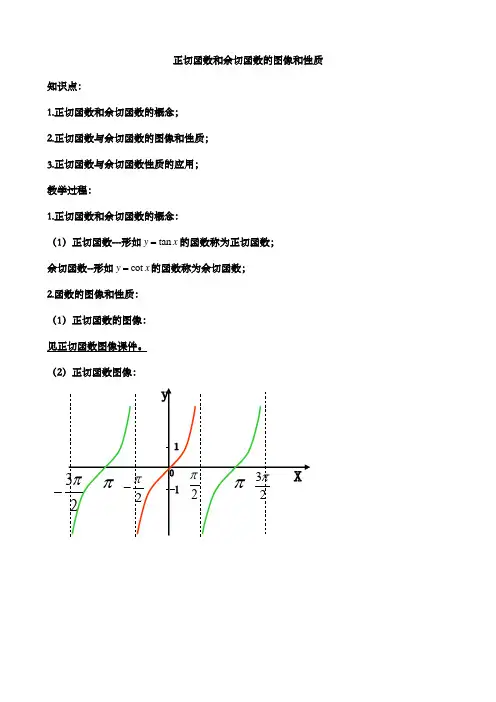
正切函数和余切函数的图像和性质知识点：1.正切函数和余切函数的概念；2.正切函数与余切函数的图像和性质；3.正切函数与余切函数性质的应用；教学过程：1.正切函数和余切函数的概念：（1）正切函数---形如tan=的函数称为正切函数；y x余切函数--形如cot=的函数称为余切函数；y x2.函数的图像和性质：（1）正切函数的图像：见正切函数图像课件。
（2）正切函数图像：-（3）与切函数的图像：归纳填表格：例1.求下列函数的周期： （1）tan(3)3y x π=-+；（2）221tgxy tg x=+；（3）cot tan y x x =-；（4）22tan21tan 2xy x=-； （5）sin 1tan tan 2x y x x ⎛⎫=+ ⎪⎝⎭例2.求下列函数的单调区间： （1）tan(2)24y x π=++；（2）tan()123x y π=-+-；（3）12log cot y x ⎛= ⎝⎭ 例3.求下列函数的定义域：（1）tan 4y x π⎛⎫=- ⎪⎝⎭；（2）y =（3）y = 例4.（1）求函数21)tan tan ]y x x =-的定义域； （2）解不等式：23tan (2)(3tan(2)044x x ππ+-+≤例5.已知2tan tan y x a x =-，当1[0,],[0,]34x a π∈∈时，函数max y =a 的值；例6.已知函数tan ,(0,)2y x x π=∈，若1212,(0,),2x x x x π∈≠。
求证：1212()()()22f x f x x xf ++>。
正切、余切函数的图象和性质
正切、余切函数的图象和性质
正切、余切函数的图象和性质
张思明
教学目的：（略）
教学过程择录：
一、引题：
师：对比上一节的习题，请同学们看一看自己的作业本，对正弦和余弦函数，在作业中，我们已涉及了多少类型的问题？
生众：P159（11）正弦，余弦函数的定义域：
P158（3）正弦，余弦函数的最值（值域）：
P158（6）正弦，余弦函数的奇偶性
P159（8）正弦，余弦函数的单调性
P159（7）正弦，余弦函数的应用一-----比大小
P158（4）正弦，余弦函数的周期（最小正周期）
P159（12）正弦，余弦函数的图象
P160（16、17）正弦，余弦函数性质的应用
教师在黑板上书写：（1）定义域（2）值域（3）奇偶性（4）单调性（5）比大小（6）求最小正周期（7）作图（8）应用教师：今天我们来学习正切、余切函数的图象和性质，可以想一想，我们要觖决什么问题？
生众：不就是上面这几点问题吗？
教师：说的不错，我们就是要来解决把“正弦、余弦函数”换成“正切、余切函数”后（1）~（7）后面加一个“是什么？”这样一些问题。
请同学们带的这些问题看书5分钟（P153~P157）。
[评述]：这里是通过作业小结的方式引入问题。
学生常常是很肓目的做作业，很少观察作业所涉及的问题类型和范围。
教师有意识地引导学生作这种观察，既培养了学生看课本的习惯，又自然引出了今天的课题和要探索解决的问题。
二、学生自己回顾
[1] [2] [3] [4] [5]。
三角函数的图象与性质教学目标1．熟练掌握正弦函数、余弦函数、正切函数、余切函数的性质，并能用它研究复合函数的性质．2．熟练掌握正弦函数、余弦函数、正切函数、余切函数图象的形状、态度，并会用“五点法”画出函数y=sin(ωx+φ)的图象。
3．理解图象平移变换、伸缩变换的意义，并会用这两种变换研究函数图象的变化．重点难点重点是通过复习，能运用四种三角函数的性质研究复合三角函数的性质及图象的特点，特别是三角函数的周期性，是需要重点明确的问题．难点是，在研究复合函数性质时，有些需要先进行三角变换，把问题转化到四种三角函数上，才能进行研究，这就增加了问题的综合性和难度．教学过程三角函数的图象与性质是三角函数的核心问题，要熟练、准确地掌握．特别是三角函数的周期性，反映了三角函数的特点，在复习“三角函数的性质与图象”时，要牢牢抓住“三角函数周期性”这一内容，认真体会周期性在三角函数所有性质中的地位和作用．这样才能把性质理解透彻．【要点复习】一.y=sinx的图象和性质：1．图象：列表后描点，用平滑曲线相连得到y=sinx，x∈［0，2π］的图象y=sinx，x∈R时的完整的图象．由此可见，画出y=sinx 的图象关键是首先要画出y=sinx 在［0，2π］内的图象．而y=sinx 在［0，2π］的图象有这样五个点很重要：(0,0),(2π,1),(π，0)，（32π，-1），（2π，0）；其中(0,0), (π，0)，（2π，0）是轴上的点，(2π,1), （32π，-1）分别是函数图象的最高、最低点．所以这五个点是确定y=sinx 图象的基本点．因此，代数描点法也可简称为“五点法”，以后再画y=sinx 图象时，就可直接使用五点法了．2．性质：（1）定义域：x ∈R ．（2）值域：y ∈［-1，1］, ∴y=sinx 是有界函数。
（3）周期性：正弦函数y=sinx 是周期函数．2π是它的最小正周期，2k π（k ∈Z ，k ＝0）都是它的周期．（4）单调性：从图象上可以看出正弦函数在整个实数域上不是增函数，也不是减函数，但具有增减区间。
板块一 基础知识一、锐角三角函数的定义1. 锐角A 的正弦、余弦、正切、余切都叫做A ∠的锐角三角函数．2. 正弦：Rt ABC ∆中，锐角A 的对边与斜边的比叫做A ∠的正弦，记作sin A ，即sin aA c =． 3. 余弦：Rt ABC ∆中，锐角A 的邻边与斜边的比叫做A ∠的余弦，记作cos A ，即cos b A c =． 4. 正切：Rt ABC ∆中，锐角A 的对边与邻边的比叫做A ∠的正切，记作tan A ，即tan a A b =． 5. 余切：Rt ABC ∆中，锐角A 的邻边与对边的比叫做A ∠的余切，记作cot A ，即cot b A a=． 从定义中可以看出，① 正弦、余弦、正切、余切都是在直角三角形中给出的，要避免应用时对任意三角形随便套用定义． ② sin A 、cos A 、tan A 、cot A 分别是正弦、余弦、正切、余切的数学表达符号，是一个整体，不能理解为sin 与A 、cos 与A 、tan 与A 、cot 与A 的乘积．③ 在直角三角形中，正弦、余弦、正切、余切分别是某个锐角的对边与斜边、邻边与斜边、对边与邻边、邻边与对边的比值，当这个锐角确定后，这些比值都是固定值．二、特殊角三角函数这些特殊角的三角函数值一定要牢牢记住．三、锐角三角函数的取值范围在Rt ABC ∆中，90C ∠=︒，000a b c a c b c >>><<，，，，，又sin a A c =，cos b A c =，tan a A b =，cot bA a=，三角函数 0︒ 30︒45︒60︒90︒sin A 012 22 321cos A 132 22 12 0tan A 03313-cot A - 3 1 33三角函数所以0sin 10cos 1tan 0cot 0A A A A <<<<>>，，，．四、三角函数关系 1. 同角三角函数关系： 22sin cos 1A A +=，sin tan cos AA A=，tan cot 1A A ⋅= 2. 互余角三角函数关系：⑴ 任意锐角的正弦值等于它的余角的余弦值：()sin cos 90A A =︒-； ⑵ 任意锐角的余弦值等于它的余角的正弦值：()cos sin 90A A =︒-； ⑶ 任意锐角的正切值等于它的余角的余切值：()tan cot 90A A =︒-；⑷ 任意锐角的余切值等于它的余角的正切值：()cot tan 90A A =︒-． 3. 锐角三角函数值的变化规律：令1c =，锐角A ∠越小，则a 越小，则b 越大；当A ∠越大，则a 就越大，b 就越小，且a c b c <<，，所以当角度在0~90︒︒范围内变化时，正弦值随角度的增大（或减小）而增大（或减小）；余弦值随角度的增大（或减小）而减小（或增大）．而正切值也是随角度的增大（或减小）而增大（或减小）；余切值随角度的增大（或减小）而减小（或增大）．可以应用0~90︒︒间的正弦值、余弦值、正切值、余切值的增减性来比较角的正弦、余弦、正切、余切值的大小，其规律是：⑴A B 、为锐角且A B >，则sin sin A B >，cos cos A B <，tan tan A B >，cot cot A B <；⑵A B 、为锐角且A B <，则sin sin A B <，cos cos A B >，tan tan A B <，cot cot A B >．该规律反过来也成立．板块二 常用公式1. 和角公式：cos()cos cos sin sin αβαβαβ+=-，sin()sin cos cos sin αβαβαβ+=+，tan tan tan()1tan tan αβαβαβ++=-⋅；2. 差角公式：cos()cos cos sin sin αβαβαβ-=+，sin()sin cos cos sin αβαβαβ-=-，tan tan tan()1tan tan αβαβαβ--=+⋅；3. 倍角公式：2222cos2cos sin 2cos 112sin ααααα=-=-=-，sin22sin cos ααα=，22tan tan 21tan ααα=-； 4. 半角公式：21cos cos 22αα+=，21cos sin 22αα-=，sin 1cos tan 21cos sin ααααα-==+； 5. 万能公式：22tan2sin 1tan 2ααα=+，221tan 2cos 1tan 2ααα-=+，22tan2tan 1tan 2ααα=-；6. 积化和差公式：1cos cos [cos()cos()]2αβαβαβ=++-，1cos sin [sin()sin()]2αβαβαβ=+--，1sin cos [sin()sin()]2αβαβαβ=++-，1sin sin [cos()cos()]2αβαβαβ=-+--．7. 和差化积公式：cos cos 2cos cos22αβαβαβ+-+=，cos cos 2sin sin22αβαβαβ+--=-，sin sin 2sin cos22αβαβαβ+-+=，sin sin 2cossin22αβαβαβ+--=．板块一、三角函数基础【例1】 已知如图：在Rt ABC ∆中，810BC AC ==，.求sin A 和sin B 的值。
余切函数的特性解析与变化规律余切函数（cot）是三角函数的一种，它表示正切函数（tan）的倒数。
在数学中，余切函数的特性及其变化规律具有一定的重要性。
本文将对余切函数的特性进行解析，并讨论其变化规律。
一、余切函数的定义余切函数cot(x)表示正切函数tan(x)的倒数，即cot(x) = 1/tan(x)。
然而，由于在某些特定的角度值上正切函数为零，因此在这些角度处无定义。
这些特定角度被称为余切函数的奇点。
二、余切函数的周期性余切函数具有周期性，且其周期等于π。
这意味着当x增加π，或减去π的整数倍时，余切函数的值会重复。
例如，cot(x) = cot(x + π) = cot(x - π)。
三、余切函数的图像余切函数的图像具有一些显著特点。
当x接近奇点时，余切函数的值会趋向正无穷大或负无穷大。
当x不是奇点时，余切函数的值在正无穷到负无穷之间变化。
这可以通过绘制余切函数的图像来观察到。
四、余切函数的变化规律1. 正值和负值：在第一象限和第三象限，余切函数值为正；而在第二象限和第四象限，余切函数值为负。
因此，余切函数在不同象限上的值有着不同的符号。
2. 最大值和最小值：余切函数在奇点处无定义，因此不存在最大值或最小值。
然而，在非奇点处，余切函数的值在-1和+1之间变化。
当x接近奇点时，余切函数的值趋近于无穷大。
3. 渐进线：余切函数的图像在奇点处有两条渐近线，即x = (2n +1)π/2，其中n为整数。
这两条渐近线将图像划分成多个区域。
4. 奇偶性：余切函数具有奇偶性，即cot(-x) = -cot(x)。
这意味着余切函数关于原点是奇函数，即对于任意x，cot(x) = -cot(-x)。
五、余切函数的应用余切函数在数学和物理等领域有着广泛的应用。
例如，在电路分析中，余切函数可以用来表示电阻和电抗的比值。
在三角恒等式和复数运算中，余切函数也起到重要的作用。
综上所述，余切函数cot(x)是一种具有周期性和奇偶性的三角函数。
