下载文档原格式
,m α，
,
,n β；则分别为
},m α和},n β。
当局中人Ⅰ选定纯策略i α和局中人Ⅱ选定纯策略后，就形成了一个纯局)j ，这样的纯局势共有m n ⨯个。
对任一纯局势赢得值为ij a ，称
12122
212n n m m mn a a a a a ⎤⎥⎥⎥⎥⎦
为局中人Ⅰ的赢得矩阵。
局中人Ⅱ的赢得矩阵就是当局中人Ⅰ，Ⅱ的策略集12,S S 及局中人Ⅰ的赢得矩阵对策也就给定了，记为{}12,,G S S A =。
在齐王赛马的例子中，齐王的赢得矩阵
},
,m α，
},n β，max ）
成立，记其值为）成立的纯局势()
,i j αβ**
在纯策略意义下的解（或鞍点）
},m α，},n S β，
1,2,
,,m x ∑1,2,
,,n y ∑分别称为局中人Ⅰ和Ⅱ的混合策略集分别称为局中人Ⅰ和Ⅱ的混合策略（或策略），对
),m x 可设想成当两个局中人多次重复进行对策
12,,
,m ααα的频率。
若只进行一次时对策，混合
对策可设想成局中人Ⅰ对各纯策略的偏爱程度。
求解混合策略的问题有图解法，迭代法、线性方程组法和线性规划法，在。
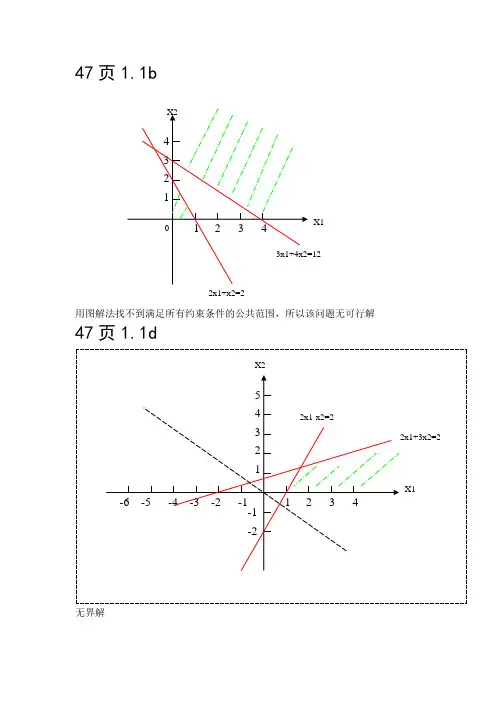
胡运权运筹学第五版答案【篇一：运筹学基础及应用第四版胡运权主编课后练习答案】xt>习题一 p46 1.1 (a)412该问题有无穷多最优解，即满足4x1z?3。
6x26且0?x2?的所有?x1,x2?，此时目标函数值(b)用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解。
1.2(a) 约束方程组的系数矩阵12a833106?403000200??0?1t最优解x??0,10,0,7,0,0?。
(b) 约束方程组的系数矩阵1a222314??2??最优解1.3(a)(1) 图解法11??2x??,0,,0?5?5?t。
最优解即为?3x14x295x12x28的解x31,2，最大值z352(2)单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 max z?10x1?5x2?0x3?0x4?3x1?4x2?x3?9s.t. ?5x12x2x48则p3,p4组成一个基。
令x1?x2?0得基可行解x??0,0,9,8?，由此列出初始单纯形表12。
??min?898,53?520，??min?2183,??142?2?新的单纯形表为1,20，表明已找到问题最优解x1?1, x2?32,x3?0 , x4?0。
最大值z*352(b) (1) 图解法6x1?2x2x1?x2?最优解即为?6x12x224x1?x2?5的解x73,22?，最大值z172(2) 单纯形法首先在各约束条件上添加松弛变量，将问题转化为标准形式 max z?2x1?x2?0x3?0x4?0x55x2?x3?15??s.t. ?6x1?2x2?x4?24xxx5125则p3，p4，p5组成一个基。
令x1?x2?0得基可行解x??0,0,15,24,5?，由此列出初始单纯形表12。
??min??,245?,??461?155,24,20，??min?3?32?2新的单纯形表为【篇二：运筹学基础及应用第四版胡运权主编课后练习答案】xt>习题一 p46 1.1 (a)41的所有?x1,x2?，此时目标函数值2该问题有无穷多最优解，即满足4x1?6x2?6且0?x2?z?3。
运筹学教程胡运权第5版1. 简介《运筹学教程》是一本经典的运筹学教材，由胡运权教授编写，已经出版了第5版。
本教程旨在介绍运筹学的基本概念、方法和应用，帮助读者掌握运筹学的基本原理和技巧。
2. 内容概述本教程分为十个章节，涵盖了运筹学的主要内容。
第一章：运筹学概述本章介绍了运筹学的基本概念和发展历程，阐述了运筹学在现代管理决策中的重要作用。
第二章：线性规划本章介绍线性规划的基本概念、模型和求解方法，包括单纯形法和对偶理论等内容。
第三章：整数规划本章介绍整数规划的基本概念和求解方法，包括分枝定界法和割平面法等内容。
第四章：非线性规划本章介绍非线性规划的基本概念和求解方法，包括梯度法和牛顿法等内容。
第五章：动态规划本章介绍动态规划的基本概念和求解方法，包括最优子结构和状态转移方程等内容。
第六章：网络优化本章介绍网络优化的基本概念和求解方法，包括最小生成树和最短路问题等内容。
第七章：多目标规划本章介绍多目标规划的基本概念和求解方法，包括帕累托最优解和权衡法等内容。
第八章：排队论本章介绍排队论的基本概念和模型，包括利用泊松分布和指数分布建模等内容。
第九章：库存管理本章介绍库存管理的基本概念和模型，包括经济订货量和安全库存等内容。
第十章：决策分析本章介绍决策分析的基本概念和方法，包括决策树和期望值法等内容。
3. 学习目标通过学习本教程，读者可以掌握以下技能：•理解运筹学的基本概念和方法；•掌握线性规划、整数规划、非线性规划等方法的应用；•学会运用动态规划、网络优化、多目标规划等方法解决实际问题；•掌握排队论、库存管理、决策分析等方法的应用。
4. 使用说明读者可以将本教程作为自学资料，按照章节顺序逐步学习。
每个章节都包括基本概念的讲解、求解方法的介绍和案例分析。
在阅读本教程时，读者可以使用Markdown文本格式进行标注和整理笔记。
Markdown具有简单易学、格式清晰的特点，适合用于文档编写和批注。
5. 结语《运筹学教程》是一本经典的运筹学教材，适合作为运筹学的入门教材或者参考资料。
