当前位置：文档之家 › 胡运权《运筹学教程》(第5版)配套题库-考研真题精选及课后习题(第一~三章)【圣才出品】

胡运权《运筹学教程》(第5版)配套题库-考研真题精选及课后习题(第一~三章)【圣才出品】

  • 格式：pdf
  • 大小：2.70 MB
  • 文档页数：113

下载文档原格式

  / 113

合集下载

《运筹学教程》胡云权-第五版-运筹学复习

《运筹学教程》胡云权-第五版-运筹学复习

x6
10
[2]
-5
1
0
-1
1
5
3M+2
3-4M
2M-5
0
-M
0
-z
-M
x4
2
0
[7/2 ]
1/2
1
1/2
-1/2
4/7
2
x1
5
1
-5/2
1/2
0
-1/2
1/2
-
0
7M/2+8
M/2-6
0
M/2+1
-3M/2-1
-z
3
x2
4/7
0
1
1/7
2/7
1/7
-1/7
2
x1
45/7
1
0
6/7
5/7
-1/7
1/7
✓ 右端项非负
解的重要概念
可行解（或可行点）：满足所有约束条件的向量 x ( x1 , x 2 , x n )
可行域：所有的可行解的全体
D { x Ax b, x 0}
最优解：在可行域中目标函数值最大（或最小）的可行解，最优解的全体
称为最优解集合
O {x D c x c y, y D }
0
x3
0
x4
0
x5

9
4
3
4
5
[ 10 ]
1
0
0
0
1
0
0
0
1
90
40
30
7
12
0
0
0
1
90
bi
360

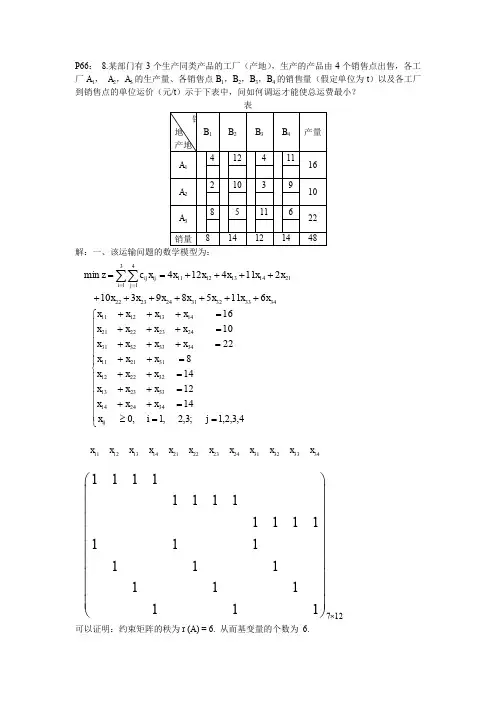
运筹学(胡运权版)第三章运输问题课后习题答案

运筹学(胡运权版)第三章运输问题课后习题答案

P66： 8.某部门有3个生产同类产品的工厂（产地），生产的产品由4个销售点出售，各工厂A 1， A 2，A 3的生产量、各销售点B 1，B 2，B 3，B 4的销售量（假定单位为t ）以及各工厂到销售点的单位运价（元/t ）示于下表中，问如何调运才能使总运费最小？表解：一、该运输问题的数学模型为：可以证明：约束矩阵的秩为r (A) = 6. 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解（初始调运方案）1. 最小元素法思想：优先满足运价（或运距）最小的供销业务。

其余（非基）变量全等于零。

此解满足所有约束条件，且基变量（非零变量）的个数为6（等于m+n-1=3+4-1=6).总运费为（目标函数值） ,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x ∑∑===3141i j ijij x c Z2. 伏格尔（Vogel)法伏格尔法的基本思想：运输表中各行各列的最小运价与次小运价之差值（罚数）应尽可能地小。

或者说：优先供应罚数最大行（或列）中最小运费的方格，以避免将运量分配到该行（或该列）次小运距的方格中。

运筹学基础及应用第五版 胡运权第三章

运筹学基础及应用第五版 胡运权第三章

例3
设有三个化肥厂供应四个地区的农用化肥，假
定等量的化肥在这些地区使用效果相同，已知各化肥厂 年产量，各地区年需要量及从各化肥厂到各地区单位化 肥的运价表如下，试决定使总的运费最节省的化肥调拨 方案。
解：这是一个产销不平衡的运输问题，总产量为
160万t，四个地区最低需求为110万t ，最高需求为无限。 当其它地区都是满足最低需求时，第Ⅳ地区每年最多能 分配到60万t ，这样最高需求就是210万t，大于产量。 为建立产销平衡表，在表中增加一假想化肥厂D ， 其年产量为50万t 。并把各地区的最低需求和额外需求 区分开来，建立产销平衡表。
例1
现在把问题概括一下，在线性规划中我们研究这样 一类运输问题：有某种物资需要调运，这种物资的计量
单位可以是重量、包装单位或其他。已知有m个地点可以
供应该种物资（以后通称产地，用 i 1,, m 表示），有 n个地点需要该种物资（以后通称销地，用 j 1,, n 表示），又知这m个产地的可供量（以后通称产量）为 （可通写为 a i ），n个销地的需要量（以后 a1 , a2 ,, am
第三章 运输问题
§1．运输问题的典例和数学模型
§ 2．表上作业法
§ 3．产销不平衡的运输问题及其应用
§1．运输问题的典例和数学模型
某食品公司经销主要产品之一是糖果，它下面 设有三个加工厂，每天的糖果生产量分别为： A1 7t ， A3 9t。该公司把这些糖果分别运往四个地区 A2 4t ， 的门市部销售，各地区每天的销售量： B1 3t ， B2 6t， B4 6t 。已知从每个加工厂到各销售门市部每 B3 5t， 吨糖果的运价如下表： 单位：元/t
产 销 平 衡 表
当一个产地的产量不能运往某一个销地的时候，认为 运价为M(表示任意大正数)。额外需求部分的销量，由于 是否满足都可以，所以假想厂运往这些销地的运价定为 0。

运筹学(胡运权)第五版课后答案-运筹作业

运筹学(胡运权)第五版课后答案-运筹作业

运筹学(胡运权)第五版课后答案-运筹作业47页1.1b用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解47页1.1d无界解1 2 3 454321-1-6 -5 -4 -3 -2X2X12x1--2x1+3x1 2 3 44321X12x1+x2=23x1+4x2=X1.2（b）约束方程的系数矩阵A= 1 2 3 42 1 1 2P1 P2 P3 P4基基解是否可行解目标函数值X1 X2 X3 X4P1 P2 -4 11/2 0 0 否P1 P3 2/5 0 11/5 0 是43/5 P1 P4 -1/3 0 0 11/6 否P2 P3 0 1/2 2 0 是 5 P2 P4 0 -1/2 0 2 否P3 P4 0 0 1 1 是 5最优解A=(0 1/2 2 0)T和(0 0 1 1)T49页13题设Xij为第i月租j个月的面积minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x1 3 +6000x23+7300x14s.t.x11+x12+x13+x14≥15x12+x13+x14+x21+x22+x23≥10x13+x14+x22+x23+x31+x32≥20x14+x23+x32+x41≥12Xij≥0用excel求解为：( )用LINDO求解：LP OPTIMUM FOUND AT STEP 3 OBJECTIVE FUNCTION V ALUE1) 118400.0V ARIABLE V ALUE REDUCED COSTZ 0.000000 1.000000X11 3.000000 0.000000X21 0.000000 2800.000000X31 8.000000 0.000000X41 0.000000 1100.000000X12 0.000000 1700.000000X22 0.000000 1700.000000X32 0.000000 0.000000X13 0.000000 400.000000X23 0.0000001500.000000X14 12.000000 0.000000ROW SLACK OR SURPLUS DUAL PRICES2) 0.000000 -2800.0000003) 2.000000 0.0000004) 0.000000 -2800.0000005) 0.000000 -1700.000000NO. ITERATIONS= 3答若使所费租借费用最小，需第一个月租一个月租期300平方米，租四个月租期1200平方米，第三个月租一个月租期800平方米，50页14题设a1，a2，a3, a4, a5分别为在A1, A2, B1, B2, B3加工的Ⅰ产品数量，b1，b2，b3分别为在A1, A2, B1加工的Ⅱ产品数量，c1为在A2，B2上加工的Ⅲ产品数量。

清华大学《运筹学教程》胡运权主编课后习题答案

清华大学《运筹学教程》胡运权主编课后习题答案

3 x1 x2 x5 3
st
4 x1 3 x2 x3 x6
x1
2 x2
x4
4
6
x j 0（, j 1,,4）
cj
CB
xB
b
-M x5 3
-M
x6
6
0
x4
4
cj zj
-4 x1 1
-M x6 2
0
x4
3
cj zj
-4
-1 0
x1
x2
x3
3
1
0
4
3 -1
1
20
7M-4 4M-1 -M
小于0 ,因此已经得到唯一最优解，最优解为：
X * 2 5 ,9 / 5,1,0T
max Z 10x1 15x2 12x3
5x1 3x2 x3 9
(4)
st
5x1 2x1
6x2 x2 x3
15x3 5
15
x j 0（, j 1,,3）
39
1.8 已知某线性规划问题的初始单纯形
表和用单纯形法迭代后得到下面表格,试求括
弧中未知数a∼l值。
项目
X1 X2 X3 X4 X5
X4 6 (b) (c) (d) 1 0
X5 1 -1 3 (e) 0 1
Cj－Zj
a -1 2 0 0
X1 (f) (g) 2 -1 1/2 0
X5 4 (h) (i) 1 1/2 1
Cj－Zj
0 -7 (j) (k) (l)
6 4
x1 , x2 0
无穷多最优解
(蓝 色 线 段 上 的 点 都 是 最优 解 ）
x1
6 5
,
x2

《运筹学(胡运权)》第五版课后习题答案

《运筹学(胡运权)》第五版课后习题答案
X2 0.000000 2.000000
X33.000000 0.000000
X1,X2,X3 0.000000 0.000000
ROW SLACK OR SURPLUS DUAL PRICES
2) 0.000000 0.200000
3) 0.000000 0.600000
4) 0.0000000.000000
6) 0.0000000.008571
7) 0.000000 0.110000
8) 0.000000 -1.500000
NO. ITERATIONS= 6
计算lindo截屏
2.1a:
对偶问题为：
maxz=2y1+3y2+5y3
s.t.
y1+2y2+y3≤2
3y3+y2+4y3≤2
4y1+3y2+3y3=4
A1 1200.000000 0.000000
A2 0.000000 9.640000
A3 285.714294 0.000000
B3 10000.0000000.000000
C1 0.000000 15.900000
B1 0.000000 0.230000
A4 342.857147 0.000000
X2 1.000000 2.000000 INFINITY
X3 4.000000 1.000000 1.500000
X1,X2,X3 0.000000 0.000000 INFINITY
RIGHTHAND SIDE RANGES
ROW CURRENT ALLOWABLE ALLOWABLE
RHS INCREASE DECREASE

(完整版)运筹学胡运权第五版课件(第1章)

(完整版)运筹学胡运权第五版课件(第1章)
四运筹学研究的基本特点?系统的整体优化?多学科的配合?模型方法的应用五五运筹学研究的基本步骤运筹学研究的基本步骤?分析与表述问题?建立数学模型?对问题求解?对模型和模型导出的解进行检验?建立对解的有效控制?方案的实施第一章线性规划及单纯形法linearprogrammingandsimplexmethodggp11一般线性规划问题的数学模型11问题的提出例1用一块边长为a的正方形铁皮做一个无盖长方体容器应如何裁剪可使做成的容器的容积最大
（3）L.P. 的顶点与基可行解一一对应。
§1.3 单纯形法（Simplex Method）原理
3-1 预备知识：凸集与顶点
（1）凸集：对于集合C中任意两点连线段上的点，若全在C内， 则称集合C为凸集。
直观特征：图形从内部向外部凸出。
凸集
非凸集
（2）顶点：凸集中不在任意两点的连线段内部的点。
X1
转化为
（2）若约束条件为不等式，
则依次引入松弛变量或剩余变量（统称为松弛变量），
转化为等式约束条件。
约束为≥不等式，减去松弛变量，化为等式约束条件；
多 退
约束为≤不等式，加上松弛变量，化为等式约束条件。
少 补
注意：松弛变量在目标函数中系数全为0。
例：max z=2 x1+3 x2
2 x1+2 x2 12
s.t.
4x1
16
5 x2 15
x10， x2 0
标准化
max z 2x1 3x2 0x3 0x4 0x5
2x1 2x2 x3
12
s.t.
4
x1
5 x2
x4 16 x5 15
x1, x2 , x3, x4 , x5 0
（3）若决策变量xj≤0，则令

胡运权《运筹学教程》习题答案(第一章)[1]

胡运权《运筹学教程》习题答案(第一章)[1]

第一章习题解答1.1 用图解法求解下列线性规划问题。

并指出问题具有惟一最优解、无穷多最优解、无界解还是无可行解。

+=32min 21x x Z +=23max 21x x Z ⎪⎩⎪⎨⎧≥≥+≥+0,422664.)1(212121x x x x x x st ⎪⎩⎪⎨⎧≥≥+≤+0,124322.)2(212121x x x x x x st ⎪⎩⎪⎨⎧≤≤≤≤≤++=85105120106.max )3(212121x x x x st x x Z ⎪⎩⎪⎨⎧≥≤+−≥−+=0,23222.65max )4(21212121x x x x x x st x x Z 第一章习题解答无穷多最优解，,422664.32min )1(21212121⎪⎩⎪⎨⎧≥≥+≥++=x x x x x x st x x Z 是一个最优解3,31,121===Z x x 该问题无解⎪⎩⎪⎨⎧≥≥+≤++=0,124322.23max )2(21212121x x x x x x st x x Z 第一章习题解答85105120106.max )3(212121⎪⎩⎪⎨⎧≤≤≤≤≤++=x x x x st x x Z 唯最优解16,6,1021===Z x x 唯一最优解，该问题有无界解⎪⎩⎪⎨⎧≥≤+−≥−+=0,23222.65max )4(21212121x x x x x x st x x Z 第一章习题解答1.2 将下述线性规划问题化成标准形式。

1422245243min )1(432143214321⎪⎪⎧≤+−+−=−+−+−+−=x x x x x x x x x x x x Z .,0,,23243214321⎪⎪⎩⎨≥≥−++−无约束x x x x x x x x st ⎪⎩⎪⎨⎧≥≤≤−+−=++−+−=无约束321321321321,0,0624322min )2(x x x x x x x x x st x x x Z 第一章习题解答.2321422245243min )1(4321432143214321⎪⎪⎪⎨⎧≥−++−≤+−+−=−+−+−+−=x x x x x x x x x x x x st x x x x Z ,0,,4321⎪⎩≥无约束x x x x ⎪⎪⎩⎪⎪⎨⎧≥=−+−++−=+−+−+=−+−+−+−+−=0,,,,,232142222455243max 64241321642413215424132142413214241321x x x x x x x x x x x x x x x x x x x x x x x st x x x x x Z 第一章习题解答⎪⎪⎨⎧≥≤≤−+−=++−+−=无约束321321321321,0,0624322min)2(x x x x x x x x x st x x x Z ⎩⎪⎩⎪⎨⎧≥=++−+=−++−+−+=0,,,,6243322max 43231214323121323121323121x x x x x x x x x x x x x x st x x x x Z第一章习题解答634334max )3(3212121⎪⎪⎧=−+=++=x x x x x st x x Z 517,0,1,59,524,,1,0424321421=====⎪⎪⎩⎨=≥=++Z x x x x j x x x x j 该题是唯一最优解：）（"第一章习题解答⎪⎧≤++−≤++++=151565935121510max 321321x x x x x x x x x Z 该题无可行解。

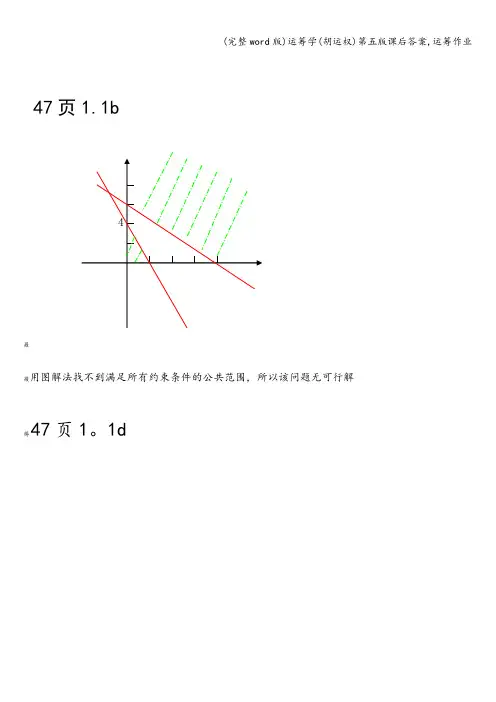
(完整word版)运筹学(胡运权)第五版课后答案,运筹作业

(完整word版)运筹学(胡运权)第五版课后答案,运筹作业

47页1.1b羅蕿用图解法找不到满足所有约束条件的公共范围，所以该问题无可行解薅47页1。

1d蒂无界解（b）衿1.2蕿约束方程的系数矩阵A=1234莇2112蚄P1P2P3P4,运筹作业肀最优解A=（01/220）T和(0011）T页13题肆49膃设Xij为第i月租j个月的面积羄minz=2800x11+2800x21+2800x31+2800x41+4500x12+4500x22+4500x32+6000x13+6000x23+7300x 14螁s.t.聿x11+x12+x13+x14≥15膃x12+x13+x14+x21+x22+x23≥10膀x13+x14+x22+x23+x31+x32≥20艿x14+x23+x32+x41≥12袇Xij≥0芃用excel求解为：薁用LINDO求解：羁LPOPTIMUMFOUNDATSTEP3薆OBJECTIVEFUNCTIONVALUE 蚇1)118400.0羂VARIABLEVALUEREDUCEDCOST 荿Z0.0000001。

000000虿X113.0000000。

000000螇X210。

0000002800。

000000莃X318。

0000000.000000肁X410.0000001100。

000000莈X120.0000001700.000000袆X220.0000001700。

000000螄X320.0000000。

000000蕿X130.000000400.000000膇X230。

0000001500。

000000袆X1412.0000000.000000袁ROWSLACKORSURPLUSDUALPRICES芁2)0。

000000—2800。

000000羆3）2.0000000.000000羆4)0。

000000—2800.000000节5）0。

000000-1700.000000蝿NO。

ITERATIONS=3罿答若使所费租借费用最小，需第一个月租一个月租期300平方米，租四个月租期1200平方米，第三个月租一个月租期800平方米,页14题肆50蚃设a1，a2，a3,a4,a5分别为在A1，A2，B1，B2，B3加工的Ⅰ产品数量，b1，b2，b3分别为在A1，A2，B1加工的Ⅱ产品数量,c1为在A2，B2上加工的Ⅲ产品数量。

胡运权运筹学第五版第一章习题讲解

胡运权运筹学第五版第一章习题讲解

1.3 答案：
●单纯形法：
Cj CB 0 0 基 x3 x4 Cj-Zj 0 x3
10
x1
Cj-Zj
8/5
1
0
2/5
1 1
0
0 5/14
1/5
-2 -3/14
5
x2
3/2
0
10
x1
Cj-Zj
1
1
0
0
0
-1/7
-5/14
2/7
-25/14
Return

课后题答案
z' -3x1 x 2 'x 2 ' '-2x 3 '0x 4 0x 5 - Mx6 - Mx7
台时 限制 6000 1000 0 4000 7000 4000
单位台 时费用 0.05 0.03 0.06 0.11 0.05
6 4 7 0.25 0.36 0.25 0.44 0.25 0.35
6 4 7 0.21 0.36 0.21 0.44 0.21 0.77
8
8 11
0.5 0.48
0.27 0.48

课后题答案
1.1（a）答案： 该问题有无穷多最优解。 取特殊值：(1.5,0) 计算目标函数最优值 得:min z=3。
1.1（a）
1.1（b）答案： 由图可知：该Lp问题没 有可行域，即可得出： 该问题无可行解
1.1(b)
Return

课后题答案
1.2（b）答案：
基解 基
x1 P2 P3 P4 P3 -4 2/5 -113 ) 10 x211 6000 7( x x x ) 9 x 12 x 121 122 123 221 322 10000 6( x111 x121 ) 8( x211 x221 ) 4000 s.t. 4( x112 x122 ) 11x322 7000 7( x113 x123 ) 4000 x111 , x112 , x113 , x121 , x122 , x123 , x211 , x221 , x322 0

运筹学基础及应用第五版胡运权第一章

运筹学基础及应用第五版胡运权第一章
问题的提出 某企业计划生产Ⅰ、Ⅱ两种产品。这两种产品都要分别在A、B、C、D四种不同设备上加工。生产每件产品Ⅰ需占用各设备分别为2、1、4、0h，生产每件产品Ⅱ，需占用各设备分别为2、2、0、4h。已知各设备计划期内用于生产这两种产品的能力分别为12、8、16、12h，又知每生产一件产品Ⅰ企业能获得2元利润，每生产一件产品Ⅱ企业能获得3元利润，问企业应安排生产两种产品各多少件，使总的利润收入为最大。
xi 0
aij
aLj
xL 0
i
∴ P1 , P2,······,PL-1, PL+1,······ Pm, Pj 线性无关。
∴ X1 也为基本可行解。
四、最优性检验和解的判别
令
，其中 随基的改变而改变
X1 = (x1 0- a1j ,x2 0- a2j ,···,xm 0- amj ,0,···,,···,0)T
必要性：X非基本可行解 X非凸集顶点 不失一般性，设X=(x1,x2,······,xm,0,0,······,0)T，为非基本可行解， ∵ X为可行解，
证：等价于 X非基本可行解X非凸集顶点
又 X是非基本可行解， ∴ P1,P2,······,Pm线性相关，即有 1P1+2P2+······+mPm=0， 其中1，2，······，m不全为0，两端同乘≠0，得 1P1+2P2+······+mPm=0，······（2）
∵ >0, 1->0 ，当xj=0， 必有yj=zj=0
∴
pjyj =
j=1
n
pjyj=b ······(1)
j=1
r
pjzj =
j=1
n
pjzj=b ······(2)

清华大学《运筹学教程》胡运权主编课后习题答案(第一章)

清华大学《运筹学教程》胡运权主编课后习题答案(第一章)

2)c=0
3)c>0
d<0 d=0 d>0
0
c 3 d 4
A1点 A1点 A3点
A2A3线段
3 c 5 4 d 2
c 5 d 2 c 5 d 2
c 3 d 4
A2点
A1A2线段 A1点
l.6 考虑下述线性规划问题：
max Z c1 x1 c2 x2 a11 x1 a12 x2 b1 st .a21 x1 a22 x2 b2 x1 , x2 0
-1
x2
0
x3
0
x4
-M
x5
-M
x6
CB
xB
x5
x6
x4
i
-M -M 0
3 6 4
[3] 4 1
1 3 2
0 -1 0
0 0 1
1 0 0
0 1 0 0
1 3/2 4 3 6/5 9/5
cj zj
7M-4
1 2 3 1 0 0 0
4M-1
1/3 [5/3] 5/3
5M/3+1/3
-M
0 -1 0 -M
0
0 0 1 0
0
1/3 -4/3 -1/3
-7M/3+4/3
-4 -M 0
x1
0
1 0 0
x6
x4
cj zj
cj
x6
是否基 可行解
Z
(x1,x2,x3)
(x1,x2,x4) (x1,x2,x5) (x1,x2,x6)
0
0 0 7/4
61/3
10 3 -4
-7/6
0 0 0

运筹学(胡运权)第五版复习提纲汇总

运筹学(胡运权)第五版复习提纲汇总

《运筹学1》复习提纲第一章线性规划和单纯形法1. 规划问题的三要素2. 线性规划问题的条件3. 线性规划问题的标准形式4. 标准化方法5.作用在目标函数中的系数松弛变量化不等式约束为等式约束0人工变量使系数矩阵有单位矩阵-M（大M法）6. 可行解、可行域、最优解7. 基、基向量、基变量、非基变量、基解、基可行解（至多个）、可行基、最优基8. 各种解之间的关系9. 图解法10. 检验数11.线性规划问题解的类型用最终表判别的方法无可行解有非0人工变量有可行解有唯一最优解无非0人工变量，非基变量的检验数全为负数有无穷多最优解无非0人工变量，非基变量的检验数全非正，且有一个非基变量的检验数为0有无界解无非0人工变量，有一个非基变量的检验数为正数且这一列的系数全非正12. 单纯形表的结构：前两行，后一行，前三列，后一列，主体部分13. 单纯形法的步骤14. 人工变量法（1）大M法（2）两阶段法15. 单纯形法的向量矩阵描述（不考）初始表中的基变量在最终表中的矩阵是B-1最终表中的基变量在初始表中的矩阵是B 课后练习1.1,1.2(b,1.3(a,1.6(a,1.7(a,1.8,1.12,1.14第二章线性规划的对偶理论1、原问题的基本形式对偶问题的基本形式2、原问题与对偶问题的互化3、对偶问题的基本性质1 弱对偶性2 最优性3 无界性4 强对偶性5 互补松弛性（由松得紧性）6 互补的基解4、利用对偶理论求最优解的方法5、影子价格6、灵敏度分析（不考）1 分析Cj，可使最优解不变2 分析bi，可使最优基不变3 增加一个变量的分析课后练习2.1(a,b,2.2,2.4,2.9(a,b,c第三章运输问题1、运输问题的已知条件：产销平衡表，单位运价表运输问题有最优解的条件：产销平衡2、m产n销的运输问题有mn个决策变量，有m+n个约束条件，有m+n-1个基变量（有数字格），有mn-(m+n-1个非基变量（空格）3、调运方案表（基可行解）：有数字格，空格4、空格的闭回路的构成闭回路的作用：1 计算检验数2 改进方案5、利用检验数判断调运方案的最优性若有负检验数，则此方案要改进；若无负检验数，则此方案为最优方案。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2．μ是关于可行流 f 的一条增广链，则在μ上有：对一切（i，j）∈μ－，有 fij＞0。（ ） [暨南大学 2019 研]
【答案】√ 【解析】由增广链定义可知，当边（i，j）属于μ的反向边集时，该条边的流量大于 0。
3．事件 j 的最早时间 TE（j）是指以事件 j 为开工事件的工序最迟必须开工时间。（ ） [暨南大学 2019 研]
零元素的最少直线数目的集合。结果如下：
4 / 113
圣才电子书 十万种考研考证电子书、题库视频学习平台

（4）在未被覆盖的元素中找最小元素，未被覆盖的行分别减去该最小元素，在出现负
数的列上整列加上最小元素，得到新矩阵 C′：
0 2 6 1 0 0 4
表 1-1-1
解：（1）先对各行减去本行的最小元素，再对各列减去本列最小元素，得到矩阵 C 如
下：
0 2 6 9
C 1 4 4 0 1 0 0 3 2 3 6 0
（2）确定独立零元素，对 C 加圈，得到
◎ 2 6 9
C
1
1
4 ◎
4
◎ 3
2
3
6
（3）由于只有 3 个独立零元素，少于系数矩阵阶数 n＝4，故需要确定能够覆盖所有
A．没有无穷多最优解 B．没有最优解 C．有无界解 D．有最优解 【答案】B 【解析】有最优解的前提是有可行解，该题无可行解，则也无最优解。
2．如果某种资源的影子价格大于其市场价格，则说明（ ）。[暨南大学 2019 研] A．该资源稀缺 B．该资源过剩 C．企业应尽快处理该资源 D．企业应充分利用该资源，开辟新的生产途径 【答案】A 【解析】当资源的影子价格不为 0 时，表明该种资源在生产中已耗费完毕；且若影子 价格大于其市场价格，说明企业应买进该种资源，该种资源稀缺。
图 1-1-1 解：将最短路问题分为 4 个阶段，第一阶段状态为 A，第二阶段状态为 B、C，第三阶 段状态为 D，第四阶段状态为 E、F。采用逆序算法： 当 k＝4 时，f4（E）＝276，f4（F）＝186； 当 k＝3 时，f3（D）＝min{d（D，E）＋ f4（E）， d（D，E）＋ f4（F）}＝min{58 ＋276，110＋186}＝296，路径为 D→F→G； 当 k＝2 时，f2（B）＝min{d（B，E）＋ f4（E）， d（B，D）＋ f3（D）}＝min{300 ＋276，350＋296}＝576，路径为 B→E→G； f2（C）＝ d（C，D）＋ f3（D）＝241＋296＝537，路径为 C→D→F→G； 当 k＝1 时，f1（A）＝min{ d（A，B）＋ f2（B）， d（A，C）＋ f2（C）}＝min{404 ＋576，479＋537}＝980，路径为 A→B→E→G ∴点 A 到点 G 的最短路径为 A→B→E→G，共 980 公里。
1 2 5
0
（5）对其加圈，得到：
◎ 2 6 10
C 1
3 ◎
3
4
1
2
5 ◎
（6）同样发现独立零元素个数小于阶数，重复步骤（3）、（4），可得最终加圈矩阵 C″：
◎ 0 4 10
C
0
3
1 1 ◎ 0 ◎ 6
1
◎
3
0
或
0 ◎ 4 10
C ◎ 3
1 0
1 ◎
0
6
1
0
3 ◎
最优指派方案有两种：
3 / 113
圣才电子书 十万种考研考证电子书、题库视频学习平台

单时差等于其紧后工作的最早开工时间与本工作的最早完工时间之差。
四、计算题
1．有 4 个工人，要指派他们分别完成 4 种工作，每人做各种工作所消耗的时间如表 1-1-1 所示，问指派哪个人去完成哪种工作，可使总的消耗时间为最小？[北京邮电大学 2018 研]
圣才电子书

十万种考研考证电子书、题库视频学习平台
第一部分 考研真题精选
一、判断题
1．要求不超过第一目标值、恰好完成第二目标值，目标函数是 min z＝p1d1＋＋p2（d2 －－d2＋）。（ ）[暨南大学 2019 研]
【答案】× 【解析】不超过第一目标值、恰好完成第二目标值的目标函数应为 min z＝p1d1＋＋p2 （d2－＋d2＋）。
2．简述后悔值决策准则。[南京航空航天大学 2018 研] 答：后悔值决策准则基本思想在于尽量减少决策后的遗憾，使决策者不后悔或少后悔。 具体计算时，先根据效益矩阵最大值减去矩阵中的每个数，得到后悔矩阵；再取各方案最大 后悔值，最后取不同方案最大后悔值中的最小值，以该方案作为最优方案。
3．简述工序单时差。[南京航空航天大学 2018 研] 答：工序单时差指在不影响紧后工资的最早开工时间条件下，该工作可以延迟其开工时 间的最大幅度，用 r（i，j）表示。其计算公式为：r（i，j）＝tES（j，k）－tEF（i，j），即
3．表上作业法中初始方案均为（ ）。[暨南大学 2019 研] A．最优解 B．非可行解
2 / 113
圣才电子书

C．待改进解
十万种考研考证电子书、题库视频学习平台
D．可行解
【答案】D
【解析】表上作业法迭代过程中得出的所有解都是运输问题的基可行解。
三、简答题
1．简述增广链的概念。[南京航空航天大学 2018 研] 答：设 f 是一个可行流，vs 是网络的起点，vt 是网络的终点，μ是从 vs 到 vt 的一条链， 若μ满足下列条件： （1）在弧（vi，vj）∈μ＋上，0≤fij＜cij，即μ＋中每一前向弧是非饱和弧。 （2）在弧（vi，vj）∈μ－上，0＜fij≤cij，即μ－中每一后向弧是非零流弧。 称μ是关于可行流 f 的一条增广链。
①甲－A，乙－D，丙－C，丁－B
②甲－B，乙－A，丙－C，丁－D
5 / 113
圣才电子书 十万种考研考证电子书、题库视频学习平台

最小总消耗时间均为 70。
2．图 1-1-1 中每条边上的数字表示边的长度（单位：公里），求点 A 到点 G 的最短路 径（写出过程）。[中山大学 2019 研]
【答案】× 【解析】事件 j 的最早时间 TE（j）表明以它为始点的各工作最早可能开始的时间，也 表示以它为终点的全部工作的最早可能完成时间。
二、选择题
1 / 113
圣才电子书 十万种考研考证电子书、题库视频学习平台

1．若线性规划问题没有可行解，可行解集是空集，则此问题（ ）。[暨南大学 2019 研]