走进美妙的数学花园-真题

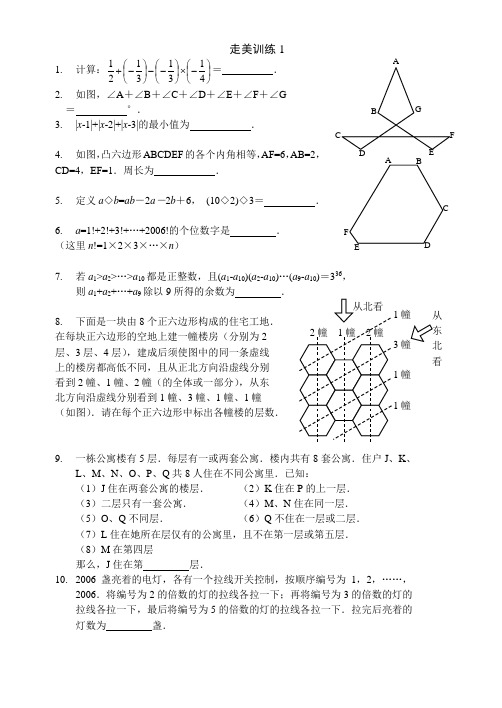
走美训练11. 计算：⎪⎭⎫⎝⎛-⨯⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-+41313121＝ ．2. 如图，∠A ＋∠B ＋∠C ＋∠D ＋∠E ＋∠F ＋∠G ＝ °．3. |x -1|+|x -2|+|x -3|的最小值为 ．4. 如图，凸六边形ABCDEF 的各个内角相等，AF=6，AB=2，CD=4，EF=1．周长为 ．5. 定义a ◇b =ab －2a －2b ＋6， (10◇2)◇3＝ ．6. a =1!+2!+3!+…+2006!的个位数字是 ． （这里n !=1×2×3×…×n ）7. 若a 1>a 2>…>a 10都是正整数，且(a 1-a 10)(a 2-a 10)…(a 9-a 10)＝336，则a 1+a 2+…+a 9除以9所得的余数为 ．8. 下面是一块由8个正六边形构成的住宅工地． 在每块正六边形的空地上建一幢楼房（分别为2 层、3层、4层），建成后须使图中的同一条虚线 上的楼房都高低不同，且从正北方向沿虚线分别 看到2幢、1幢、2幢（的全体或一部分），从东 北方向沿虚线分别看到1幢、3幢、1幢、1幢 （如图）．请在每个正六边形中标出各幢楼的层数．9. 一栋公寓楼有5层．每层有一或两套公寓．楼内共有8套公寓．住户J 、K 、L 、M 、N 、O 、P 、Q 共8人住在不同公寓里．已知：（1）J 住在两套公寓的楼层．（2）K 住在P 的上一层．（3）二层只有一套公寓． （4）M 、N 住在同一层． （5）O 、Q 不同层． （6）Q 不住在一层或二层． （7）L 住在她所在层仅有的公寓里，且不在第一层或第五层． （8）M 在第四层那么，J 住在第 层．10. 2006盏亮着的电灯，各有一个拉线开关控制，按顺序编号为1，2，……，2006．将编号为2的倍数的灯的拉线各拉一下；再将编号为3的倍数的灯的拉线各拉一下，最后将编号为5的倍数的灯的拉线各拉一下．拉完后亮着的灯数为 盏．1幢3 1幢 1幢从 看。

第二届“走进美妙的数学花园”中国青少年数学论坛（四年级）试题答案及解析共12题，每题10分【题1】9999×7777+3333×6666=____________。

答案：99980001解法：9999×7777+3333×6666=9999×7777+9999×2222=9999×（7777+2222）=9999×（10000－1）=99990000－9999=99980001【题2】一个七位数7272 被3除余1，被9除余4，这个数最小是____________。

答案：2004727解法：设这个七位数为7272abc7272a b c ≡1（mod3），则a+b+c ≡1（mod3） 7272abc ≡4（mod9），则a+b+c ≡4（mod9）所以，a+b+c 最小值为4故这个七位数最小为2004727。

【题3】右图是由25个边长为3 厘米的小正方形拼成，它的周长为__ ___厘米。

答案：84解法：这个图形的周长等于如图虚线正方形的周长。

3×7×4=84（厘米）【题4】甲、乙两人带着相同数量的钱一起去买练习本。

甲花光了自己所有的钱，并向乙借了1元2角，刚好买了12本。

乙剩下的钱恰好还可以买9本。

练习本的单价是_________。

答案：8角解法：甲、乙两人所带钱数相同，甲向乙借了1元2角后，甲比乙多2元4角，而甲比乙恰好多买3本练习本，故练习本的单价为8角。

1元2角=12角12×2÷（12－9）=8（角）每本练习本8角【题5】有9张纸牌，分别为1至9。

A、B、C、D四人取牌，每人取2张。

现已知A取的两张牌之和是10；B取的两张牌之差是1；C取的两张牌之积是24；D取的两张牌之商是3。

剩下的一张是___________。

答案：7解法：C取的两张牌之积是24，只能是4和6或3和8。

1、2012×9+2012×8-2012×7=2、已知a@b=2×a+b，那么99@1=3、4个一样的宽为2厘米的长方形拼成一个大长方形，大长方形的周长是厘米4、“走进美妙的数学花园”中，不同的汉字代表不同的数字，那么，走+进+美+妙+的+数+学+花+园的计算结果最小是。

5、请把1000表示成5个数的和，5个数中出现的数字完全相同，1000= + + + +6、甲、乙、丙共有99元，甲的钱比乙的钱的2倍少2元，乙的钱比丙的3倍少3元，甲有元7、袋子中有若干个球，每次拿出其中的一半又一个球，这样共操作了4次，袋中还有5个球。

袋中原有个球8、某年6月恰有5个星期一和5个星期日，这个月的15号是星期。

9、如图，一个四位数加上一个三位数和胃2012，这两个数的数字和等于。

10、10个相同的玻璃球分给3个人，每人至少一个，有不同的分配方法。

11、玉米炮有单筒玉米炮、双筒玉米炮、三筒玉米炮三种。

单筒玉米炮每次发射1根玉米，可以消灭8个僵尸；双筒玉米炮每次发射2根玉米，每根玉米消灭7个僵尸，玉米炮一共发射5次，发射玉米11根，至少消灭个僵尸。

12、有五个互不相等的非零自然数，如果其中一个减少45，另外四个数都变成原先的2倍，那么得到的仍然是这5个数，这五个数的总和是。

13、一个三位数，等于它的数字和的13，这样的三位数有个，分别是。

14、国际象棋中，皇后可以沿横线、竖线、斜线吃子，在4×4的棋盘中最多可以放入皇后，它们相互之间不能吃子，在图中给出你的放法（用“O”表示）15、11个方格从左到右排列，左边的5个方格中已各放了1枚棋子（3白2黑），每次操作必须同时移动2枚相邻的黑白棋子到2个相邻的空格中，但不能交换这2枚棋子的左右顺序，要把这五枚柜子全部放到右边5个方格中，且2枚黑子在最右边2格，至少移动次。

“走进美妙数学花园”决赛六年级试题一、填空题（共12题，第1～4题每题8分）1、计算：314×31.4+628×68.6+68.6×686=（ ）。

2、将一个长28cm,宽18cm 的长方形铁片的四个角各截去一个边长为4cm 的正方形,再将此铁片折成一个无盖的长方形容器。

容器的容积为（ ）立方厘米。

3、一个长方形和一个等腰三角形如图放置，图中六块的面积分别为1，1，1，1，2，3。

大长方形的面积是（ ）。

4、一个数n 的数字中为奇数的那些数字的和记为S(n)，为偶数的那些数字的和记为E(n)。

例如S(134)=1+3=4，E(134) =4。

S(1)+ S(2) +……+S(100)= （ ）。

E (1)+E(2) +……+E(100)= （ ）。

5、今有A 、B 两个港口，A 在B 的上游60千米处。

甲、乙两船分别从A 、B 两港同时出必，都向上游航行。

甲船出发时，有一物品掉落水中，浮在水面，随水流漂往下游。

甲船出发航行一段后，调头去追落水的物品。

当甲船追上落水物品时，恰好和乙船相遇。

已知甲、乙两船在静水中的航行速度相同，且这个速度为水速的6倍。

当甲船调头时，甲船已航行（ ）千米。

6、一个两位数，数字和是质数。

而且，这个两位数分别乘以3，5，7之后，得到的数的数字和都仍为质数，满足条件的两位数为（ ）。

7、N 是一个各位数字互不相等的自然数，它能被它的每个数字整除。

N 的最大值是（ ）。

8、4支足球队单循环赛，每两队都赛一场，每两队都赛一场，每场胜者得3分，负者得0分，平局各得1分。

比赛结束4支队的得分恰好是4个连续自然数。

第四名输给第（ ）名。

9、如图，正方形ABCD 的边长为6，AE=1.5，CF=2。

长方形EFGH 的面积为（ ）。

10、小王8点骑摩托车从甲地出发前往乙地，8点15追上一个早已从甲地出发的骑车人。

小李开大客车从甲地出发前往乙地，8点半追上这个骑车人。

第五届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛初赛八年级试卷（B 卷）姓名填空题（共14题，满分150.第1-4题每题8分，第5-8题每题10分，第9-12题每题12分，第13~14题每题15分） 1. 求9+49+299+8999+99999= .2. 一个百位为1的三位数，等于它的三个数的立方和.这个三位数是 .3. 在某架无刻度的天平上称量重物，有1克，2克，3克，15克，40克的砝码各一个.如果天平两端均可放置砝码，那么，可以称出的重物的克数有 种.4. 金与银做成的王冠重250克，放在水中减轻16克.已知金在水中轻119，银在水中轻110.这块王冠中金 克，银 克.5. x 、y 、z 为实数且x+y+z=，则x+y+z= .6. 301010107⎡⎤⎢⎥+⎣⎦的个位数为 . 其中[ x]表示x 的整数部分. 7. 若a 3ab -+2（-3）=0, 则()()()()()()11111122a 12b 12ab a b a b ++++=++++++ .8. 整数x 、y 满足等式 22744,x y x y x y ++=++的值是 . 9. 一个直角三角形三边的长a 、b 、c 都是整数，且满足()()()()()()1111ab a 1b 1a 22a 12b 12b ++++++++++= .10. 已知1. 2256x 3x x 2x 3--+-= .11.自然数N 被2、3、4、5、6、7、8、9整除，前四位为2007. N 的最小值为 .12. 正整数数列n A 满足：n 3n 2n 1n n 1n n 123A A A A A A ++++=≥=（+），，，，， . 已知6A =8820，7A = .13. 一个长方形和一个等腰直角三角形如图 放置， 图中的5个阴影三角形的面积各不相等，且从小到大构成等差数列.其中S 是等差数列中的第 列.14. 如下表，在77⨯的正方形表格中又9个数和4个字母，其中J 、Q 、K 都表示10，A 既可以表示1也可以表示11.将数或字母在原来的列中移动，设法使数与字母的总数多于1的每行、每列斜线上的数与字母的和等于21.将你的结果填在右图中.第五届“走进美妙的数学花园”中国青少年数学论坛趣味解题技能展示八年级参考答案14、。

第六届“走进美妙数学花园”六年级决赛试题一、填空题Ⅰ(每题8分，共40分)1、算式(2022-9)÷0.7÷1.1的计算结果是。

2、全世界胡杨90%在中国，中国胡杨90%在新疆，新疆胡杨90%在塔里木，塔里木的胡杨占全世界的 %。

3、半径为10、20、30的三个扇形如下列图放置，S2是S1的倍。

4、50个不同的正整数，它们的总和是2022，那么这些数里奇数至多有个。

5、A、B、C三队竞赛篮球，A队以83∶73战胜B队，B队以88∶79战胜C队，C队以84∶76战胜A队，三队中得失分率的出线。

一个队的得失分率为(得的总分)/(失的总分)，如，A队得失分率为(83+76)/(73+84)。

三队中队出线。

二、填空题Ⅱ(每题10分，共50分)6、如图，一个边长为120cm的等边三角形被分成了面积相等的五等份，那么，AB= cm。

7、某校六年级学生中男生占52%，男生中爱踢球的占80%，女生中不爱踢球的占70%。

那么，在该校六年级全体学生中，爱踢球的学生占 %。

8、在每个方框中填入一数字，使得乘法竖式成立。

已知乘积有两种不同的得数，那么这两个得数的差是。

9、大小一样的金、银、铜、铁、锡正方体各一个，拼成如图的十字，一共有种不同的拼法(旋转后可以重合的拼法看成是一样的拼法)。

10、在右图的每个格子中填入1～的一个，使得每行、每列所填的数字各不一样。

每个粗框左上角的数和“+”、“-”、“×”、“÷”分别表示粗框内所填数字的和、差、积、商(例如“600×”表示它所在的粗框内的四个数字的乘积是600)。

三、填空题Ⅲ(每题12分，共60分)11、用1、3、5、7、9这五个数字组成若干个合数，每个数字恰好用一次。

那么，这些合数的总和最小是。

12、图1盒子高为20cm，底面数据如图2，这个盒子的容积是 cm3。

(π取3.14)13、一件工程按甲、乙、丙各一天的挨次工作，恰需要成天数工作完毕。

第三-六届“走进美妙数学花园”六年级决赛试题及答案-第三届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛决赛小学六年级试卷一、填空题（共10道题，每题10分）1、印度也像中国一样有着灿烂的文化，古代印度有这样一道有趣的数学题：有一群蜜蜂，其中1/5落在牡丹花上，1/3落在栀子花上，这两者的差的三倍，飞向月季花，最后剩下一只小蜜蜂在芳香的茉莉花和玉兰花之间飞来飞去，共有（）只蜜蜂。

2、在甲容器中装有浓度为10.5%的盐水90毫升，乙容器中装有浓度为11.7%的盐水210毫升，如果先从甲、乙容器中倒出同样多的盐水，再将它们分别倒入对方的容器内搅匀，结果得到浓度相同的盐水，各倒出了（）毫升盐水。

3、在下图中，A为半径为3的⊙O外一点，弦BC∥AO且BC=3。

连结AC。

阴影面积等于（）（∏取3.14）4、用0～9这10个数字组成若干个质数,每个数字都恰好用一次,这些质数的和最小是（）。

5、从上海开车去南京，原计划中午11：30到达，但出发后车速提高了1/7，11点钟就到了，第二天返回时，同一时间从南京出发，按原速行驶了120千米后，再将车速提高1/6，到达上海时恰好11：10，上海、南京两市间的路程是（）千米。

6、将0～9这10个数字填入下图的方框中，使得等式成立，现在已经填入“3”，请将其他9个数字填入（注：首位不能为0）（□□□+□-□□）×3□÷□□=20057、一些士兵排成一列横队，第一次从左到右1至4报数，第二次从右到左1至6报数，两次都报3的恰有5名，这列士兵最多有（）名。

8、两个长方形如图摆放，M为AD的中点，阴影部分的面积=（）。

9、把一个大长方体木块表面上涂满红色后，分割成若干个棱长为1的小正方体，其中恰有两个面涂上红色的小正方体恰好是2005块，大长方体体积的最小值是（）。

10、如图，6个3×2的小方格表拼成了6×6的大方格表，请在空白处填入1～6中的数，使得每行、每列中的数各不相同，并且原来6个3×2的小方格表中的数也各不相同。

第八届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示初赛四年级试卷（A卷）一、填空题I1.4⨯=____________-2102010÷0.252.今年某地举行一位名人的一百多年诞辰纪念，这位名人的诞辰年代是四位数，其中有两个相邻的数相同，这四个数字的和是24，这位名人诞生于__________年。

3.下面算式中，每个字代表一个数字，不同的字代表不同的数字。

求“走”+“进”+“美”+“妙”+“数”+“学”+“花”+“园”+“好”=_____________4.上半场湖人队以68:59领先骑士队，第三节骑士队以98:96反超。

问：第三节这一节骑士队胜湖人队_________分。

5.2010年是虎年，请把1,3,5，……，21这11个奇数不重复地填入虎额上的“王”字中，使三行、一列的和都等于35。

二、填空题II6.下面的算式中，相同字母表示相同的数字，不同的字母表示不同的数字。

两位数EF=________7．如图，在连接正六边形的3个顶点而成的三角形中，与正六边形有公共边的三角形有_________个。

8．小青蛙沿着台阶往上跳，每跳一次都比上一次升高4厘米，它从离地面10厘米处开始跳，这一处称为小青蛙的第一次的落脚点，那么它的第100个落脚点正好在台阶尽头的亭子内，这亭子距地面_________厘米。

9．小姑娘先写出她母亲的年龄，接着在后面写上她自己的年龄，构成一个4位数，然后从这个4位数中减去她们的年龄差，得到数4289，这个小姑娘________岁。

10．一个自然数，它加上1是2的倍数，它的2倍加上1是3的倍数，它的3倍加上1是5的倍数。

这样的自然数中最小的一个是__________。

三、填空题III11．小辉的语文作业本上抄写了若干句三字经和千字文，三字经3字一句，千字文4字一句，语文老师数了一遍，三字经和千字文总共是95句，其中三字经的字数比千字文字数的3倍多60个字，小辉的作业本上三字经有_______句，千字文有_______句。

第十四届“走进美妙的数学花园”上海初赛三年级试题详解一、填空题（每小题8分，共40分）【第1题】20×16＋1－10=______。

《考点》整数计算〖解析〗原式＝320－10＋1＝311【第2题】一群鸡和兔子，共有48只脚，兔子有4只，鸡有______只。

《考点》鸡兔同笼、应用题〖解析〗兔子有4只，兔子共有4×4＝16只脚，那么鸡就共有48－16＝32只脚，所以鸡有32÷2＝16只。

【第3题】洋洋说，爸爸比我大24岁，明年爸爸的年龄正好是我的4倍，洋洋今年______岁。

《考点》年龄问题〖解析〗明年爸爸的年龄正好是我的4倍，此时年龄差仍为24岁，所以洋洋今年24÷（4－1）－1＝7岁。

【第4题】根据图中给出的相关数字，下面图形的周长是______。

《考点》巧求周长〖解析〗本题可以采取平移法或标向法。

这里用标向法来解，箭头向右的线段长度之和等于箭头向左的线段长度之和，箭头向上的线段长度之和等于箭头向下的线段长度之和，所以算此图形的周长只需算两个方向线段的长度，即向下（下）和向右（左），图形的周长是（8＋5＋12）×2＝50。

【第5题】在小于2016的正整数中，被63除后，商和余数相同的数有______个。

《考点》余数问题〖解析〗2016÷63＝32，商最大为31，最小为1，所以商和余数相同的数有31个。

二、填空题（每小题10分，共50分）【第6题】右图的两个竖式中，相同的汉字代表相同的数字，不同的汉字代表不同的数字，那么六位数美妙数学花园＝。

《考点》数字迷〖解析〗法一：由右图可以得到学＋园＝10，数＋花＝10，那么数、花同奇或同偶，所以数－花一定是偶数，学要向数借1才可以减园，即10＋学－园＝6，所以园＝7，学＝3。

由此可以推出数－1－花＝1或10＋数－1－花＝1，（1）若数－花＝2，那么数＝6，花＝4，妙＝0，美＝2，美妙数学花园＝206347。

第二届“走进美妙的数学花园”中国青少年数学论坛（三年级）试题答案及解析共12题,每题10分【题1】2999+999×999= 。

答案：1001000解法：2999+999×999=2000+999×（1+999）=2×1000+999×1000=1000×（2+999）=1001000【题2】2×3×5×7×11×13×17÷（2004－2）= 。

答案：255解法：2×3×5×7×11×13×17÷（2004－2）=（2×3×5×17）×（7×11×13）÷2002=510×1001÷（2×1001）=255【题3】一串黑白珠子穿在一起（如下图），共有108个。

这串珠子中白珠子有_________只。

答案：43解法：这串珠子从第3个开始每5个为一组（3黑2白）循环出现，108=3+5×21，共有21组多3个，所以白珠子有2×21+1=43（只）。

【题4】将1~9这9个数字填入下图的9个圆圈内，使得每条线段两端上的两个数字之和各不相同（即得到12个不同的和）。

答案：如图【题5】下图可沿格线分成三块，然后拼成一个正方形。

请将第一块的方格都标上“1”，第二块的方格都标上“2”。

答案：如图【题6】鸡兔共27只，兔的脚比鸡的脚多18只。

兔_ _____只。

答案：12解法：假设这27只全是兔，则兔的脚比鸡的脚多27×4－0=108（只），而实际上只多18只。

故鸡有（108－18）÷（4+2）=15（只）则兔有27－15=12（只）。

【题7】两筐苹果一样重。

第一筐卖出8千克，第二筐卖出16千克。

ABCD第十一届“走进美妙的数学花园”青少年展示交流活动趣味数学解题技能展示小学六年级试卷（B 卷）一、填空题 I （每题 8 分，共 40 分）1. 183⨯ 279⨯361-182⨯ 278⨯360 的计算结果是（填写 A 、B 、C 、D 四个字母中的一个）A.217017B.207217C.207216D.217016【考点】计算 【难度】☆☆ 【答案】A【分析】若学生对代数比较熟练，可以用(a +1)(b +1)(c +1) = abc + ab + bc + ca + a + b + c +1来减少计算量．2. 假设地球是个均匀的球体（半径 6378 千米），围绕地球赤道正上方上有一圈铁丝，铁丝的周长比地球赤道长 1 米，在赤道和铁丝之间会有一个缝隙，下列动物中，有 种可以安全通过铁丝．①蚂蚁；②蜜蜂；③青蛙；④老鼠；⑤猫；⑥成年奶牛；⑦大象 【考点】圆 【难度】☆☆ 【答案】5【分析】设地球周长为 a 米，铁丝周长为 a +1 米，那么通过c = πd 可知，铁丝的直径比地球直径 1多了 π米，缝隙的高度为该值的一半，约为 16 厘米，所以前四个动物都可以通过．至于猫能不能通过就看出题人想法了．3. 将 0-5 这六个数字中的 4 个数字填入由图的圆圈中，没条线段两端的数字作差（大或小），可以得到 5 个差，这 5 个查恰好为 1-5.在所有满足条件的填法中，四位数 ABCD （首位不能为 0）的最小值 是 ．【考点】数字谜 【难度】☆☆ 【答案】1052【分析】让四位数最小，那么 A 为 1，B 为 0，又因为必须有一个差为 5，故而 CD 中有一个是 5．若C 为5，那么D 只能为2 或3；若D 为5，那么C 无解；故而最小值为1052．4.一次考试中，总人数的1又3 人得了3 分，总人数的1又4 人得了4 分，总人数的1又5 人得了3 4 55 分，其余人都得2 分．已知得2 分的人数和得5 分的人数一样多，则有人得了4 分．【考点】比例应用题【难度】☆☆【答案】259【分析】设总人数为60 份，那么3 分的是20 份+3 人，4 分的是15 份+4 人，5 份的是12 份+5 人，剩下2 分的是13 份-12 人，5 分和2 分一样多，所以1 份是17 人，4 分人数为15⨯17 +4=259 人．5.在一个长20 米、宽8 米、深1.6 米的长方体游泳池的四壁及地面贴瓷砖，瓷砖是边长为0.2 米的正方形，共需瓷砖块．【考点】立体几何【难度】☆☆【答案】6240【分析】地面上横向100 块，纵向40 块，共4000 块；四壁高为8 块，共8⨯（100+40）⨯2=2240块，所有的瓷砖为6240 块．二、填空题II（每题10 分，共50 分）6.如右图所示，正方形的边长是20 厘米，阴影部分面积为平方厘米．（π取3.14）【考点】圆【难度】☆☆【答案】400【分析】阴影面积=四个小半圆面积+正方形面积-大圆面积，而方外圆面积是方内圆面积两倍，且两个小半圆可组成一个方内圆，故而阴影部分面积=正方形面积，为400．7.两个相同的玻璃被，都装满了糖水，糖与水的质量比分别是1:7 和1:9，现将这两杯糖水混合，混合后糖水的含糖率是％．【考点】比例【难度】☆☆2 0＋13【答案】11.25【分析】设原来每个杯子 40 份液体，那么第一杯 5 份糖，第二杯 4 份糖，混合后共 80 份液体，9 份糖，含糖量为9 ÷80⨯100% =11.25%8. 一个游戏需要 8 人参加，分成红、黄两队，每队各 4 人，一对兄弟来参加这个游戏，他们俩很想被分在同一队，但是谁被编入哪个队是完全随机的，那么这对兄弟被分进同一队的可能性是 【考点】概率 【难度】☆☆ 3【答案】73【分析】不管第一个兄弟在哪个队，该队都剩下 3 个空位，第二个兄弟进入这个空位的概率就是79. 将数字 1-9 填入右图算式的 9 个方格中，每个数字只能用一次，算式中和的最大值为．【考点】数字谜 【难度】☆☆ 【答案】3972【分析】让和最大，则和的百位为 9，若和的十位不为 8，那么第二个加数百位最大为 7，但是十位无法提供进位；所以和的十位最大为 7．此时第二个加数百位为 8．第三个加数千位为 3，剩下 1、2、4、5、6．若个位没有进位，只能是2 +1+ 2 = 5 ，那么十位无法凑出和为 7．故而个位有进位， 满足要求的最大的和为12 + 804 + 3156 = 3972．10. 军区食堂晚饭需用 1000 斤大米和 200 斤小米，军需员到米店后发现米店正在促销．“大米 1 元 1斤，每购 10 斤送 1 斤小米（不足 10 斤部分不送）；小米 2 元 1 斤，每购 5 斤送 2 斤大米（不足 5斤部分不送）．军需员至少要付 元钱才能买够晚饭需用的米． 【考点】列方程解应用题、估算 【难度】☆☆☆☆ 【答案】1168【分析】仔细观察两种米的促销方法，会发现其折扣本质是相同的（如果把“10 斤大米”和“5斤小米”看做一份促销品的话，那么 10 元钱能买到的折扣都是 1 5份促销品），故不存在多买大米好还是多买小米好的问题，只需凑足所需重量，就一定是最省的方法；设买大米 x 斤，小米 y 斤，列⎨ ⎧x + 2y ≤ 1000 方程组：⎪ 51 来估算大米与小米应买多少斤；得到大致重量：大米买 950 斤，小米买 105⎪ x + y ≤ 200 ⎩10斤，此时花了 1160 元，已有 992 斤大米和 200 斤小米，再用 8 元买 8 斤大米即可，最少用 1168 元 （构造方法不唯一）.三、填空题 III （每题 12 分，共 60 分）11. 定义a &b = (a + 2)(b + 2) - 2算式1⨯3⨯5⨯7⨯9⨯11⨯13- (1&3&5&7 &9 &11）的计算结果是 ．【考点】类比与猜想 【难度】☆☆☆ 【答案】2【分析】1&3 = 3⨯5 - 2 ， 1&3&5 = (1⨯3⨯5 - 2 + 2)⨯7 - 2 =1⨯3⨯5⨯7 - 2 ……以此类推，1&3&5&7 &9&11 =1⨯3⨯5⨯7⨯9⨯11⨯13- 2，故原式答案为 2．12. 右图中共能数出个三角形．【考点】几何计数 【难度】☆☆☆☆ 【答案】76【分析】单个的三角形有 24 个，两个小三角形构成的由 24 个，三个小三角形构成的有 12 个，一个外围三角形加 3 个内圈三角形构成的有 12 个，加上两个六边形里各有两个正三角 形，共 76 个．13. 甲乙两船从一条和的 A 、B 两个码头同时出发，相向而行，甲船的静水速度比乙船的静水速度快20％，水速为乙船静水速度的 10％，两船在距离中点 10 千米处相遇．A 、B 两个码头间的距离为千米．【考点】流水行船 【难度】☆☆☆ 【答案】110【分析】设水速为 1，则乙船静水速度为 10，甲船静水速度为 12．若乙顺水甲逆水则两船在中点相遇，不符合要求，故而甲是顺水，甲速度为 13，乙速度为 9．若全程为 22 份，相遇时甲走了 13 份，故 2 份为 10 千米，全程为 110 千米．14.一个四位数，他最小的8 个约数的和是43，那么这个四位回文数是．（回文数例如：1111、4334、3210123）【考点】约数、整除性质【难度】☆☆☆☆☆【答案】2772【分析】由整除性质，4 位回文数一定是11 的倍数．若没有约数2，那么不可能满足最小8 个约数和为43；若没有约数3，1+ 2 + 4 + 5 + 7 + 8 +10 +11 = 48 > 43 ，也不满足要求．若没有约数4，1+ 2 + 3+ 5 + 6 + 7 + 9 +10 = 43 ，但是同时有约数7、9、10、11 的数只能是6930，也不满足回文数．所以约数1、2、3、4、6、11 是必须存在的．若有约数5，则一定有约数10，这个四位数个位是0，不可能是回文数．所以最小的8 个之和为43，只有1、2、3、4、6、7、9、11 这一种情况满足要求．他们最小公倍数为2772，符合回文数要求，2772 的其他倍数也不是回文数．15.小俊掷骰子游戏，刚开始他站在起点格（如图），如果他掷出1 至5 点，掷出几点就前进几格，如果他掷出 6 点或某次前进后超出终点格，则立即返回起点格；若小俊掷了四次恰好到达终点格，掷骰子的顺序有种可能．起 1 2 3 4 5 6 7 8 9 终【考点】类比与猜想【难度】☆☆☆【答案】92【分析】注意终点是10 号格．从起点出发，两次即到达终点的方法有5+5 一种．若恰好三次到达，可以第一次扔6，有1 种情况；也可以第一次不扔6，第一次扔1 有2 种、扔2 有3 种，扔3 有4种、扔4 有5 种，扔5 有4 种，共19 种．恰好四次到达，可以第二次扔后爆掉，第一次可以扔1到5 五种，也可以在第一次扔出6 爆掉，转化为3 次到达的情况，有19 种，共1+19+5+19=44 种．。

“走进美妙数学花园”决赛六年级试题共12题，每题10分1、1.25×17.6+36÷0.8+2.64×12.5=（）。

2、如图，∠A+∠B+∠C+∠D+∠E+∠F+∠G=（）。

3、下图是常见的正方体，我们可以看到三面，共有3×9=27个边长为1的正方形。

在这三面上有三条“蛇”。

每条由5个连续的正方形（每两个连续正方形有一条公共边）组成，不全在一个面上。

每两条蛇互不接触（两条蛇的方格不能有公共点）。

请将这三条蛇画出来。

4、商店一次进货6桶，重量分别为15千克、16千克、18千克、19千克、20千克、31千克。

上午卖出去2桶，下午卖出去3桶，下午卖得的钱数正好是上午的2倍。

剩下的一桶重（）千克。

5、李白提壶去买洒，遇店加一倍，见花喝一斗。

三遇店和花，喝光壶中酒。

壶中原有（）斗酒。

6、若干个硬币排成下图。

每个硬币所在行的硬币数与所在列的硬币数相减得出一个差（大数或小数），如对于a，差为7-5=2。

所有差的总和为（）。

7、有10根长度不等的木条，每根长度都是整数，最短的为1，最长的89。

现在想用其中的3根拼成一个三角形木架，但是不管怎样都不能拼成。

这10根木条中第二长的木条长（）。

8、如图，9个3×3的小方格表合并成一个9×9的大方格表。

每个格子中填入1～9中的一个数，每个数在每一行、每一列中都只出现一次，并且在原来的每个3×3的小方格表中也只出现一次。

10个“☆”处所填数的总和是（）。

9、一栋公寓楼有5层。

每层有一或两套公寓。

楼内共有8套公寓。

住户J、K、L、M、N、O、P、Q共8人住在不同公寓里。

已知：（1）J住在两套公寓的楼层。

（2）K住在P的上一层。

（3）二层只有一套公寓。

（4）M、N住在同一层。

（5）O、Q不同层。

（6）Q不住在一层或二层。

（7）L住在她所在层公有的公寓里，且不在第一层或第五层。

（8）M在第四层。

J住在第（）层里。

第六届“走进美妙的数学花园”中国青少年数学论坛趣味数学解题技能展示大赛决赛七年级试卷（B卷）一、填空题Ⅰ（每题8分，共40分）1、222222200820072006200521-+-++-=.2、A＝20072007…2007（共1000个2007），B＝20082008…2008（共1000个2008），1000A÷B的整数部分为 .3、在1、2、…、2007、2008之间添上加减号，使和的绝对值最小.算式是：. 4、将2个相同的黑球和11个相同的白球排在一个圆周上，共有种不同的排法。

（旋转，翻转相同的方法算同一种）5、在一列数11442、、、中，每连续四个数中，后三个数的积是前三个数的积的倒数。

这列数中的第100个数的积是。

二、填空题Ⅱ（每题10分，共50分）6、20082008的末两位数字为。

7、如图，四边形ABCD为正方形，AB=8，E为边CD上一点，4CE=CD，射线BE上一点F，EF=DF，∆EFD的面积为。

8、在20072008⨯的方格表上画一条对角线，这条对角线穿过个小方格。

9、正整数N是它的数字和的2008倍。

N的最小值是。

10、在1、2、3、…、2008中，取一个6的倍数，再取一个5的倍数，且这两个数的差为4。

取法共有种。

三、填空题Ⅲ（每题12分，共60分）11、将2008拆成n个自然数的和，这n个自然数的个位数字都相同。

如果将这n个数的个位数字都擦掉，剩下的数组成一个公差是6的等差数列。

n最大是。

12、梯形的上底a、下底b和高h都是整数。

下底比上底长10cm，h小于a，梯形面积是561cm2，三元整数组（,,a b h）为（写出所有可能）：13、N为正整数，且2N能被N+2008整除。

N的最小值为。

14、举出一个直角三角形，边长为整数，周长为平方数，面积是立方数。

直角三角形的三边长可以是。

15、在下图55⨯和方格中，沿着已有的线画一个简单连续的闭合圈作篱笆，篱笆不能“自身相交”。

1.走进美妙的数学世界知识纵横从蛮荒时代的结绳计数到现代通讯和信息时代神奇的数学,•人类任何时候都受到数学的恩惠和影响,数学科学是人类长期以来研究数、•量的关系和空间形式而形成的庞大科学体系.走进美妙的数学世界,我们将一起走进崭新的“代数”世界，•不断扩充的数系、奇妙的字母表示数、威力巨大的方程、不等式模型、运动变化的函数观念；走进美妙的数学世界，我们将一起走进丰富的“图形”世界，拼剪、折叠、平移、旋转，在操作与实验活动中，发现这些图形的奇妙的性质，用它们设计精美的图案；走进美妙的数学世界，我们将畅游在无边的“数据”世界，从图表中获取信息，并选择合适的图表来表达数据和信息；走进美妙的数学世界，它将开阔我们的视野，它提醒我们有无形的灵魂，它改变我们的思维方式，它涤尽我们的蒙昧与无知。

诺贝尔奖获得者、著名物理学家杨振宇说：“我赞美数学的优美和力量，它有战术的机巧与灵活，又有战略上的雄才远虑，而且，奇迹的奇迹，它的一些美妙概念竟是支配物理世界的基本结构。

”例题求解【例1】(1)我们平常用的数是十进制数,如2639=2×103+6×102+3×10+9,表示十进制的数要用10个数的数码(又叫数字):0,1,2,3……9,在电子计算机中用的是二进制,只要两个数码0和1,如二进制中101=1×22+0×21+1等于十进制的数5,•那么二进制中的1101等于十进制的数_________. (2001年浙江省金华市中考题)(2)探究数学“黑洞”：“黑洞”原指非常奇怪的天体，它体积小，密度大，•吸引力强，任何物体到了它那里都别想再“爬”出来，无独有偶，数字中也有类似的“黑洞”，满足某种条件的所有数，通过一种运算，都能被它吸进去，无一能逃脱它的魔掌，譬如：任意找一个３的倍数的数，先把这个数的每一个数位上的数字都立方，再相加，得到一个新数，然后把这个新数的每一个数位上数字再立方、求和……，重复运算下去，就能得到一个固定的数T=__________,•我们称之为数字“黑洞”。

第四届“走进美妙的数学花园-四年级四年级主试题委员会趣味数学解题技能展示大赛初赛（四年级）共12题,每题10分1.计算：110＋111＋112＋＋126＝2.在一个3某3的方格表中，除中间一格无棋子外，其余每格都有4枚一样的棋子，这样每边三个格子中都有12枚棋子。

去掉4枚棋子，请你适当调整一下，使每边三格中仍有12枚棋子，并且4个角上的棋子数仍然相等（画图表示）。

3.下图是一座迷宫，请画出任意一条从A到B的通道。

AB4.沿格线把右图分成形状大小都一样的四块。

用不同的阴影表示。

5.有一道关于蜗牛爬墙的题：“日升六尺六，夜降三尺三。

墙高一丈九，几日到顶端”。

蜗牛第天首次到顶端。

6.每只完整的螃蟹有2只螯、8只脚。

现有一批螃蟹，共有25只螯，120只脚。

其中可能有一些缺螯少脚的，但每只螃蟹至少保留1只螯、4只脚。

这批螃蟹至多有只，至少有只。

四年级主试题委员会7.如图，长方形ABCD中有一个正方形EFGH，且AF=16厘米，HC=13厘米，长方形ABCD的周长为厘米。

FBEACDGH8.右图是常见的正方体，我们可以看到三面，共有3某9=27个边长为1的正方形。

在这三面上有三条“蛇”。

每条由5个连续的正方形（每两个连续正方形有一条公共边）组成，不全在一个面上。

每两条蛇互不接触（两条蛇的方格不能有公共点）。

请将这三条蛇画出来。

（用阴影将蛇所在的正方形画出来）9.如图，9个3某3的小方格表合并成一个9某9的大方格表。

183☆☆2每个格子中填入1～9中的一个数，每个数在每一行、每571☆5964一列中都只出现一次，并且在原来的每个3某3的小方格74859☆表中也只出现一次。

10个“☆”处所填数的总和31☆4☆☆是514☆3☆6367486☆7952310.奶糖每千克24元，水果糖每千克18元。

买两种糖果花了同样多的钱，但水果糖比奶糖多4千克。

水果糖千克，奶糖千克。

811.如图，请在右图每个方框中填入一个不是8的数字，使乘法8竖式成立。