初中数学三角函数公式归纳汇总

01定义式02函数公式倒数关系：①②③商数关系：①②平方关系：①②③03诱导公式公式1：设为任意角，终边相同的角的同一三角函数的值相等：公式2：设为任意角，与的三角函数值之间的关系：公式3：任意角与的三角函数值之间的关系：公式4：与的三角函数值之间的关系：公式5：与的三角函数值之间的关系：公式6：及与的三角函数值之间的关系：记背诀窍：奇变偶不变，符号看象限，即形如（2k+1）90°±α，则函数名称变为余名函数，正弦变余弦，余弦变正弦，正切变余切，余切变正切。

形如2k×90°±α，则函数名称不变。

04基本公式【和差角公式】◆ 二角和差公式◆ 三角和公式【和差化积公式】口诀：正加正，正在前，余加余，余并肩，正减正，余在前，余减余，负正弦．【积化和差公式】【倍角公式】◆ 二倍角公式◆ 三倍角公式◆ 四倍角公式sin4a=-4*[cosa*sina*(2*sina^2-1)]cos4a=1+(-8*cosa^2+8*cosa^4)tan4a=(4*tana-4*tana^3)/(1-6*tana^2+tana^4)◆ 五倍角公式◆ 半角公式（正负由所在的象限决定）◆ 万能公式◆ 辅助角公式◆ 余弦定理◆ 三角函数公式算面积定理：在△ABC中，其面积就应该是底边对应的高的1/2，不妨设BC边对应的高是AD，那么△ABC的面积就是AD*BC*1/2。

而AD是垂直于BC的，这样△ADC就是直角三角形了，显然，由此可以得出，AD=ACsinC，将这个式子带回三角形的计算公式中就可以得到：，同理，即可得出三角形的面积等于两邻边及其夹角正弦值的乘积的一半。

◆ 公式：若△ABC中角A，B，C所对的三边是a,b,c：则S△ABC=1/2absinC=1/2bcsinA=1/2acsinB.◆ 反三角函数反三角函数主要是三个：y＝arcsin(x)，定义域[-1,1] ，值域[-π/2,π/2]y=arccos(x)，定义域[-1,1] ，值域[0,π]y=arctan(x)，定义域(-∞,+∞)，值域(-π/2,π/2)sinarcsin(x)=x,定义域[-1,1],值域【-π/2,π/2】◆ 反三角函数公式:arcsin(-x)=-arcsinxarccos(-x)=π－arccosxarctan(-x)=-arctanxarccot(-x)=π－arccotxarcsin x+arccosx=π/2=arctanx+arccotx sin(arcsinx)=x=cos(arccosx) =tan(arctanx)=cot(arccotx)当x∈〔—π/2，π/2〕时，有arcsin(sinx)=x当x∈〔0,π〕,arccos(cosx)=xx∈(—π/2，π/2),arctan(tanx)=xx∈(0，π),arccot(cotx)=x x〉0,arctanx=arctan1/x,arccotx类似若(arctanx+arctany)∈(—π/2，π/2),则arctanx+arctany=arctan(x+y/1-xy)。

初中数学三角函数公式汇总一、正弦函数公式1. 正弦函数的基本定义：在直角三角形中，对于一个锐角A，正弦函数定义为：sin A = 对边 / 斜边2. 正弦函数的倒数公式：两个锐角的正弦函数互为倒数，即：sin (90° - A) = 1 / sin A3. 正弦函数的和差公式：sin (A ± B) = sin A · cos B ± cos A · sin B4. 正弦函数的倍角公式：sin 2A = 2 · sin A · cos A二、余弦函数公式1. 余弦函数的基本定义：在直角三角形中，对于一个锐角A，余弦函数定义为：cos A = 邻边 / 斜边2. 余弦函数的倒数公式：两个锐角的余弦函数互为倒数，即：cos (90° - A) = 1 / cos A3. 余弦函数的和差公式：cos (A ± B) = cos A · cos B ∓ sin A · sin B4. 余弦函数的倍角公式：cos 2A = cos²A - sin²A = 2 · cos²A - 1 = 1 - 2 · sin²A三、正切函数公式1. 正切函数的基本定义：在直角三角形中，对于一个锐角A，正切函数定义为：tan A = 对边 / 邻边2. 正切函数的倒数公式：两个锐角的正切函数互为倒数，即：tan (90° - A) = 1 / tan A3. 正切函数的和差公式：tan (A ± B) = (tan A ± tan B) / (1 ∓ tan A · tan B)4. 正切函数的倍角公式：tan 2A = (2 · tan A) / (1 - tan²A)四、余切函数公式1. 余切函数的基本定义：在直角三角形中，对于一个锐角A，余切函数定义为：cot A = 邻边 / 对边 = 1 / tan A2. 余切函数的倒数公式：两个锐角的余切函数互为倒数，即：cot (90° - A) = 1 / cot A3. 余切函数的和差公式：cot (A ± B) = (cot A · cot B - 1) / (cot B ± cot A)4. 余切函数的倍角公式：cot 2A = (cot²A - 1) / (2 · cot A)五、正割函数和余割函数公式1. 正割函数的定义：在直角三角形中，对于一个锐角A，正割函数定义为：sec A = 斜边 / 邻边 = 1 / cos A2. 余割函数的定义：在直角三角形中，对于一个锐角A，余割函数定义为：csc A = 斜边 / 对边 = 1 / sin A以上是初中数学常见的三角函数公式汇总，这些公式在解决三角函数相关问题时非常有用。

初中三角函数常用公式大全一、基本关系式：1. 正弦定理：在任意三角形ABC中，有a/sinA=b/sinB=c/sinC=2R，其中a，b，c分别为三角形ABC的三边，A，B，C为对应的角，R为三角形的外接圆半径。

2. 余弦定理：在任意三角形ABC中，有c²=a²+b²-2abcosC。

3. 正弦公式：在任意三角形ABC中，有sinA/a=sinB/b=sinC/c。

4. 余弦公式：在任意三角形ABC中，有cosA=(b²+c²-a²)/2bc，cosB=(c²+a²-b²)/2ac，cosC=(a²+b²-c²)/2ab。

二、常用比值关系：1. 任意角的正弦公式：在直角三角形中，sinθ=对边/斜边。

2. 任意角的余弦公式：在直角三角形中，cosθ=邻边/斜边。

3. 任意角的正切公式：在直角三角形中，tanθ=对边/邻边。

4. 任意角的余切公式：在直角三角形中，cotθ=邻边/对边。

5. 任意角的正割公式：在直角三角形中，secθ=斜边/邻边。

6. 任意角的余割公式：在直角三角形中，cscθ=斜边/对边。

三、特殊角的值：1. π/6的正弦和余弦值：sin(π/6)=1/2，cos(π/6)=√3/22. π/4的正弦和余弦值：sin(π/4)=cos(π/4)=√2/23. π/3的正弦和余弦值：sin(π/3)=√3/2，cos(π/3)=1/24. π/2的正弦和余弦值：sin(π/2)=1，cos(π/2)=0。

四、和差化积公式：1. sin(A±B)=sinAcosB±cosAsinB。

2. cos(A±B)=cosAcosB∓sinAsinB。

3. tan(A±B)=(tanA±tanB)/(1∓tanAtanB)。

初中数学三角函数公式汇总0 1定义式0 2函数公式倒数关系：①②③商数关系：①②平方关系：①②③0 3诱导公式公式1：设为任意角，终边相同的角的同一三角函数的值相等：公式2：设为任意角，与的三角函数值之间的关系：公式3：任意角与的三角函数值之间的关系：公式4：与的三角函数值之间的关系：公式5：与的三角函数值之间的关系：公式6：及与的三角函数值之间的关系：记背诀窍：奇变偶不变，符号看象限，即形如（2k+1）90°±α，则函数名称变为余名函数，正弦变余弦，余弦变正弦，正切变余切，余切变正切。

形如2k×90°±α，则函数名称不变。

0 4基本公式【和差角公式】◆二角和差公式◆三角和公式【和差化积公式】口诀：正加正，正在前，余加余，余并肩，正减正，余在前，余减余，负正弦．【积化和差公式】【倍角公式】◆二倍角公式◆三倍角公式◆四倍角公式sin4a=-4*[cosa*sina*(2*sina^2-1)]cos4a=1+(-8*cosa^2+8*cosa^4)tan4a=(4*tana-4*tana^3)/(1-6*tana^2+tana^4)◆五倍角公式◆半角公式（正负由所在的象限决定）◆万能公式◆辅助角公式◆余弦定理◆三角函数公式算面积定理：在△ABC中，其面积就应该是底边对应的高的1/2，不妨设BC边对应的高是AD，那么△ABC的面积就是AD*BC*1/2。

而AD是垂直于BC的，这样△ADC就是直角三角形了，显然，由此可以得出，AD=ACsinC，将这个式子带回三角形的计算公式中就可以得到：，同理，即可得出三角形的面积等于两邻边及其夹角正弦值的乘积的一半。

◆公式：若△ABC中角A，B，C所对的三边是a,b,c：则S△ABC=1/2absinC=1/2bcsinA=1/2acsinB.◆反三角函数反三角函数主要是三个：y＝arcsin(x)，定义域[-1,1] ，值域[-π/2,π/2]y=arccos(x)，定义域[-1,1] ，值域[0,π]y=arctan(x)，定义域(-∞,+∞)，值域(-π/2,π/2)sinarcsin(x)=x,定义域[-1,1],值域【-π/2,π/2】◆反三角函数公式:arcsin(-x)=-arcsinxarccos(-x)=π－arccosxarctan(-x)=-arctanxarccot(-x)=π－arccotxarcsinx+arccosx=π/2=arctanx+arccotxsin(arcsinx)=x=cos(arccosx)=tan(arctanx)=cot(arccotx)当x∈〔—π/2，π/2〕时，有arcsin(sinx)=x当x∈〔0,π〕,arccos(cosx)=xx∈(—π/2，π/2),arctan(tanx)=xx∈(0，π),arccot(cotx)=x x〉0,arctanx=arctan1/x,arccotx类似若(arctanx+arctany)∈(—π/2，π/2),则arctanx+arctany=arctan(x+y/1-xy)。

(完整版)三角函数公式表1. 正弦函数 (sin):定义：正弦函数是直角三角形中对边与斜边的比值。

公式：sin(θ) = 对边 / 斜边范围：1 ≤ sin(θ) ≤ 1特殊值：sin(0°) = 0, sin(30°) = 1/2, sin(45°) = √2/2, sin(60°) = √3/2, sin(90°) = 12. 余弦函数 (cos):定义：余弦函数是直角三角形中邻边与斜边的比值。

公式：cos(θ) = 邻边 / 斜边范围：1 ≤ cos(θ) ≤ 1特殊值：cos(0°) = 1, cos(30°) = √3/2, cos(45°) = √2/2, cos(60°) = 1/2, cos(90°) = 03. 正切函数 (tan):定义：正切函数是直角三角形中对边与邻边的比值。

公式：tan(θ) = 对边 / 邻边范围：tan(θ) 可以取任意实数值特殊值：tan(0°) = 0, tan(30°) = 1/√3, tan(45°) = 1, tan(60°)= √3, tan(90°) 不存在（无穷大）4. 余切函数 (cot):定义：余切函数是直角三角形中邻边与对边的比值。

公式：cot(θ) = 邻边 / 对边范围：cot(θ) 可以取任意实数值特殊值：cot(0°) 不存在（无穷大）, cot(30°) = √3, cot(45°) = 1, cot(60°) = 1/√3, cot(90°) = 05. 正割函数 (sec):定义：正割函数是直角三角形中斜边与邻边的比值。

公式：sec(θ)= 1 / cos(θ)范围：sec(θ) 可以取任意实数值特殊值：sec(0°) = 1, sec(30°) = 2, sec(45°) = √2, sec(60°) = 2/√3, sec(90°) 不存在（无穷大）6. 余割函数 (csc):定义：余割函数是直角三角形中斜边与对边的比值。

初中三角函数公式及定理大全1、正弦定理：在三角形中，各边和它所对的角的正弦的比相等，即a/sinA=b/sinB=c/sinC=2R 。

（其中R为外接圆的半径），2、第一余弦定理：三角形中任意一边等于其他两边以及对应角余弦的交叉乘积的和，即a=c cosB + b cosC。

初中三角函数公式及定理大全1锐角三角函数定义:锐角角A的正弦(sin),余弦(cos)和正切(tan),余切(cot)以及正割(sec)，余割(csc)都叫做角A的锐角三角函数。

正弦(sin)：对边比斜边，即sinA=a/c余弦(cos)：邻边比斜边，即cosA=b/c正切(tan)：对边比邻边，即tanA=a/b余切(cot)：邻边比对边，即cotA=b/a正割(sec)：斜边比邻边，即secA=c/b余割(csc)：斜边比对边，即cscA=c/a初中三角函数公式及定理大全2互余角的关系sin(π-α)=cosα, cos(π-α)=sinα,tan(π-α)=cotα, cot(π-α)=tanα.积的关系sinα=tanα·cosαcosα=cotα·sinαtanα=sinα·secαcotα=cosα·cscαsecα=tanα·cscαcscα=secα·cotα初中三角函数公式及定理大全3平方关系sin^2(α)+cos^2(α)=1tan^2(α)+1=sec^2(α)cot^2(α)+1=csc^2(α)倒数关系tanα·cotα=1sinα·cscα=1cosα·secα=1初中三角函数公式及定理大全4三角函数的和差化积公式sinA+sinB=2sin[(A+B)/2]cos[(A-B)/2]sinA-sinB=2cos[(A+B)/2]sin[(A-B)/2]cosA+cosB=2cos[(A+B)/2]cos[(A-B)/2]cosA-cosB=-2sin[(A+B)/2]sin[(A-B)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB) tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)。

初中数学必背三角函数公式大全初中数学必背的知识点，三角函数公式大全同学们总结归纳过吗?如果没有快来小编这里瞧瞧。

下面是由小编为大家整理的“初中数学必背三角函数公式大全”，仅供参考，欢迎大家阅读。

初中数学必背三角函数公式大全常用三角函数公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosBtanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB- ctgA+ctgBsin(A+B)/sinAsinB拓展阅读：三角函数导数公式大全(sinx)' = cosx(cosx)' = - sinx(tanx)'=1/(cosx)^2=(secx)^2=1+(tanx)^2 -(cotx)'=1/(sinx)^2=(cscx)^2=1+(cotx)^2 (secx)'=tanx·secx(cscx)'=-cotx·cscx(arcsinx)'=1/(1-x^2)^1/2(arccosx)'=-1/(1-x^2)^1/2(arctanx)'=1/(1+x^2)(arccotx)'=-1/(1+x^2)(arcsecx)'=1/(|x|(x^2-1)^1/2)(arccscx)'=-1/(|x|(x^2-1)^1/2)(sinhx)'=coshx(coshx)'=sinhx(tanhx)'=1/(coshx)^2=(sechx)^2(coth)'=-1/(sinhx)^2=-(cschx)^2(sechx)'=-tanhx·sechx(cschx)'=-cothx·cschx。

tan( α+β+γ)=(tan α+tan β+tan γ-tan α· tanβ· tanγ) ÷ (1tan α· tanβ-tan β· tanγ-tan γ· tanα)
5 、幂级数
c0+c1x+c2x2+...+cnxn+...=
∑cnxn (n=0.. ∞)
c0+c1(x-a)+c2(x-a)2+...+cn(x-a)n+...=
90 ° -(60 ° -a)]sin[-90
° +(60 ° +a)] =-4cosacos(6
a)[-cos(60
° +a)] =4cosacos(60
° -a)cos(60
上述两式相比可得： tan3a=tana · tan(60 ° +a)
· tan(60 ° -a)
6、四倍角公式
sin4a=-4*[cosa*sina*(2*sina^2-1)] cos4a=1+(-8*cosa^2+8*cosa^4) tan4a=(4*tana-4*tana^3)/(1-6*tana^2+tana^4)
1
三角函数公式
一、定义公式
锐角三角函数 任意角三角函数
正弦（ sin ） 余弦（ cos ） 正切（ tan 或 tg ） 余切（ cot 或 ctg ） 正割（ sec ） 余割（ csc） 正弦（ sin ） 余弦（ cos ） 正切（ tan 或 tg ） 余切（ cot 或 ctg ） 正割（ sec ） 余割（ csc）
在任意△ ABC 中，角 A 、 B 、 C 所对的边长分别为 a 、 b 、 c ， 三角形 外接圆的半径为 R．则有：

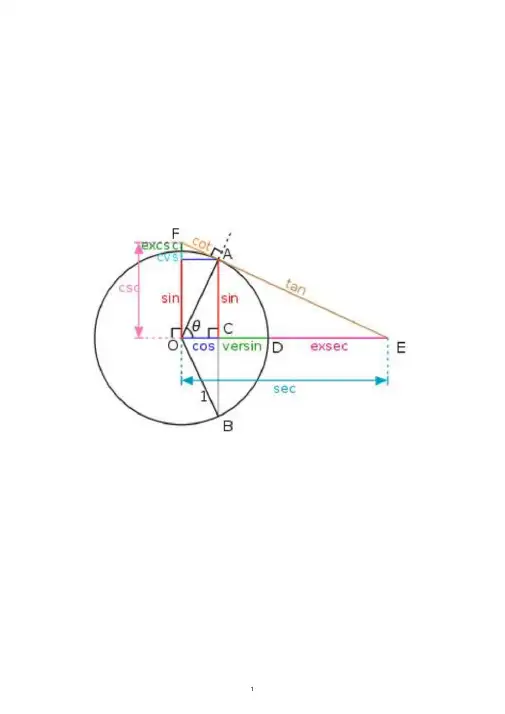
三角函数公式一、任意角的三角函数在角α的终边上任取．．一点),(y x P ,记：22y x r +=， 正弦函数：ry=αsin 余弦函数：r x =αcos 正切函数：x y =αtan余切函数：y x =αcot 正割函数：xr=αsec 余割函数：yr=αcsc 二、同角三角函数的基本关系式六边形记忆法：图形结构“上弦中切下割,左正右余中间1”；记忆方法“对角线上两个函数的积为1；阴影三角形上两顶点的三角函数值的平方和等于下顶点的三角函数值的平方；任意一顶点的三角函数值等于相邻两个顶点的三角函数值的乘积。

”倒数关系：1csc sin =⋅x x ,1sec cos =⋅x x ，1cot tan =⋅x x 。

商数关系：x x x cos sin tan =，xxx sin cos cot =。

平方关系：1cos sin 22=+x x ，x x 22sec tan 1=+，x x 22csc cot 1=+。

积的关系：sinx=tanx·cosx cosx=sinx·cotx tanx=sinx·secxcotx=cosx·cscx secx=tanx·cscx cscx=secx·cotx三、诱导公式公式一：设α为任意角,终边相同的角的同一三角函数的值相等:sin （2kπ＋α）＝sinα cos（2kπ＋α）＝cosαtan （2kπ＋α）＝tanα cot（2kπ＋α)＝cotα (其中k ∈Z) 公式二：设α为任意角，π＋α的三角函数的值与α的三角函数值之间的关系： sin （π＋α）＝－sinα cos（π＋α）＝－cosα tan （π＋α）＝tanα cot（π＋α）＝cotα公式三：任意角α与－α的三角函数值之间的关系： sin （－α）＝－sinα cos（－α）＝cosα tan(－α）＝－tanα cot（－α）＝－cotα公式四：利用公式二和公式三可以得到π－α与α的三角函数值之间的关系： sin （π－α）＝sinα cos（π－α）＝－cosα tan （π－α）＝－tanα cot(π－α）＝－cotα 公式五：απ-2与α的三角函数值之间的关系:sin （απ-2）＝cosα cos（απ-2）＝sinα tan （απ-2）＝cotα cot（απ-2）＝tanα公式六:απ+2与α的三角函数值之间的关系:sin （απ+2）＝cosα cos（απ+2）＝－sinαtan(απ+2)＝－cotα cot（απ+2）＝－tanα公式七：απ-23与α的三角函数值之间的关系： sin(απ-23）＝－cosα cos（απ-23）＝－sinαtan （απ-23)＝cotα cot（απ-23）＝tanα公式八：απ+23与α的三角函数值之间的关系：sin(απ+23）＝－cosα cos（απ+23）＝sinαtan （απ+23）＝－cotα cot（απ+23）＝－tanα公式九：利用公式一和公式三可以得到2π－α与α的三角函数值之间的关系： sin （2π－α)＝－sinα cos(2π－α）＝cosα tan （2π－α)＝－tanα cot（2π－α）＝－cotα⑴παk 2+)(Z k ∈、α-、απ+、απ-、απ-2的三角函数值,等于α的同名函数值，前面加上一个把α看成．．锐角时原函数值的符号。

初中三角函数公式大全初中阶段主要学习的三角函数公式有正弦定理、余弦定理、正切定理以及诱导公式等。

下面将分别介绍这些公式。

一、正弦定理正弦定理是用来求解三角形的边长和角度的重要公式。

设三角形ABC的边长分别为a、b 和c，对应的角度分别为A、B和C，则正弦定理可以表示为：a/sinA = b/sinB = c/sinC根据正弦定理，如果我们已知两个角和它们对应的两条边的长度，可以通过公式求解第三条边的长度；如果我们已知一个角和它对应的两条边的长度，可以通过公式求解另外两个角的大小。

二、余弦定理余弦定理是在已知三角形的两边和夹角情况下，求解第三边的长度的重要公式。

设三角形ABC的边长分别为a、b和c，对应的角度分别为A、B和C，则余弦定理可以表示为：c² = a² + b² - 2abcosC根据余弦定理，如果我们已知三角形的两边和它们之间的夹角，可以通过公式求解第三边的长度；如果我们已知三角形的三个边长，可以通过公式求解任意一个角的大小。

三、正切定理正切定理是在已知三角形的两边和夹角情况下，求解切线斜率的重要公式。

设三角形ABC 的边长分别为a、b和c，对应的角度分别为A、B和C，则正切定理可以表示为：tanA = a/b根据正切定理，如果我们已知三角形的两边和它们之间的夹角，可以通过公式求解切线斜率；如果我们已知切线斜率和其中一条边的长度，可以通过公式求解夹角的大小。

四、诱导公式诱导公式是将不常用的角度转换为常用角度的公式，常用的诱导公式如下：sin(π-x) = sinxcos(π-x) = -cosxtan(π-x) = -tanxsin(π+x) = -sinxcos(π+x) = -cosxtan(π+x) = tanxsin(2π-x) = -sinxcos(2π-x) = cosxtan(2π-x) = -tanx其中，x为任意角度。

这些公式可以帮助我们在解决三角函数问题时进行角度的转化，简化计算过程。

三角函数公式总结三角函数是数学中重要的概念之一，广泛应用于几何学、物理学等领域。

通过对三角函数的深入理解和掌握，可以大大提高我们解决各种实际问题的能力。

本文将对常见的三角函数公式进行总结，并介绍其应用。

一、正弦函数公式正弦函数是三角函数中最常见的函数之一，表示为sin(x)。

在直角三角形中，正弦函数可以定义为对边与斜边之比。

正弦函数公式可以由勾股定理推导而得。

1. 正弦函数的基本关系：sin(x) = 对边 / 斜边2. 正弦函数的周期性：sin(x + 2π) = sin(x)3. 正弦函数的奇偶性：4. 正弦函数的和差公式：sin(x + y) = sin(x)cos(y) + cos(x)sin(y)sin(x - y) = sin(x)cos(y) - cos(x)sin(y)二、余弦函数公式余弦函数是三角函数中的另一个重要概念，表示为cos(x)。

在直角三角形中，余弦函数可以定义为邻边与斜边之比。

余弦函数公式也可以通过勾股定理得到。

1. 余弦函数的基本关系：cos(x) = 邻边 / 斜边2. 余弦函数的周期性：cos(x + 2π) = cos(x)3. 余弦函数的奇偶性：4. 余弦函数的和差公式：cos(x + y) = cos(x)cos(y) - sin(x)sin(y)cos(x - y) = cos(x)cos(y) + sin(x)sin(y)三、正切函数公式正切函数表示为tan(x)，可以定义为正弦函数与余弦函数的商。

正切函数在解决角度问题时特别有用。

1. 正切函数的基本关系：tan(x) = 正弦函数 / 余弦函数2. 正切函数的周期性：tan(x + π) = tan(x)3. 正切函数的奇偶性：tan(-x) = -tan(x)4. 正切函数的和差公式：tan(x + y) = (tan(x) + tan(y)) / (1 - tan(x)tan(y))tan(x - y) = (tan(x) - tan(y)) / (1 + tan(x)tan(y))四、其他三角函数公式除了正弦函数、余弦函数和正切函数，还有其他一些常见的三角函数公式。

(完整版)初中三角函数公式表一、三角函数的基本定义在初中数学中，三角函数主要涉及正弦函数（sin）、余弦函数（cos）和正切函数（tan）。

这些函数与直角三角形的三边长度有着密切的关系。

1. 正弦函数（sin）：正弦函数表示直角三角形中，对应于一个锐角的斜边与斜边与邻边之比。

公式为：sin(θ) = 对边 / 斜边。

2. 余弦函数（cos）：余弦函数表示直角三角形中，对应于一个锐角的邻边与斜边之比。

公式为：cos(θ) = 邻边 / 斜边。

3. 正切函数（tan）：正切函数表示直角三角形中，对应于一个锐角的斜边与邻边之比。

公式为：tan(θ) = 对边 / 邻边。

二、三角函数的相互关系1. 正弦函数和余弦函数的关系：sin(θ) = cos(90° θ)，cos(θ) = sin(90° θ)。

2. 正切函数和余弦函数的关系：tan(θ) = sin(θ) / cos(θ)。

3. 正切函数和正弦函数的关系：tan(θ) = sin(θ) / cos(θ)。

三、三角函数的特殊值1. 0°：sin(0°) = 0，cos(0°) = 1，tan(0°) = 0。

2. 30°：sin(30°) = 1/2，cos(30°) = √3/2，tan(30°) =1/√3。

3. 45°：sin(45°) = √2/2，cos(45°) = √2/2，tan(45°)= 1。

4. 60°：sin(60°) = √3/2，cos(60°) = 1/2，tan(60°) = √3。

5. 90°：sin(90°) = 1，cos(90°) = 0，tan(90°) 无定义。

四、三角函数的周期性三角函数具有周期性，即函数值在一定的周期内会重复出现。

三角函数公式大全锐角三角函数公式sin α=∠α的对边/ 斜边cos α=∠α的邻边/ 斜边tan α=∠α的对边/ ∠α的邻边cot α=∠α的邻边/ ∠α的对边倍角公式Sin2A=2SinA CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1tan2A=2tanA/1-tanA^2注：SinA^2 是sinA的平方sin2A三倍角公式sin3α=4sinα·sinπ/3+αsinπ/3-αcos3α=4cosα·cosπ/3+αcosπ/3-αtan3a = tan a ·tanπ/3+a·tanπ/3-a三倍角公式推导sin3a=sin2a+a=sin2acosa+cos2asina辅助角公式Asinα+Bcosα=A^2+B^2^1/2sinα+t,其中sint=B/A^2+B^2^1/2cost=A/A^2+B^2^1/2tant=B/AAsinα+Bcosα=A^2+B^2^1/2cosα-t,tant=A/B降幂公式sin^2α=1-cos2α/2=versin2α/2cos^2α=1+cos2α/2=covers2α/2tan^2α=1-cos2α/1+cos2α推导公式tanα+cotα=2/sin2αtanα-cotα=-2cot2α1+cos2α=2cos^2α1-cos2α=2sin^2α1+sinα=sinα/2+cosα/2^2=2sina1-sin²a+1-2sin²asina=3sina-4sin³acos3a=cos2a+a=cos2acosa-sin2asina=2cos²a-1cosa-21-sin²acosa=4cos³a-3cosasin3a=3sina-4sin³a=4sina3/4-sin²a=4sina√3/2²-sin²a=4sinasin²60°-sin²a=4sinasin60°+sinasin60°-sina=4sina2sin60+a/2cos60°-a/22sin60°-a/2cos60°-a/2=4sinasin60°+asin60°-acos3a=4cos³a-3cosa=4cosacos²a-3/4=4cosacos²a-√3/2²=4cosacos²a-cos²30°=4cosacosa+cos30°cosa-cos30°=4cosa2cosa+30°/2cosa-30°/2{-2sina+30°/2sina-30°/2}=-4cosasina+30°sina-30°=-4cosasin90°-60°-asin-90°+60°+a=-4cosacos60°-a-cos60°+a=4cosacos60°-acos60°+a上述两式相比可得tan3a=tanatan60°-atan60°+a半角公式tanA/2=1-cosA/sinA=sinA/1+cosA;cotA/2=sinA/1-cosA=1+cosA/sinA.sin^2a/2=1-cosa/2cos^2a/2=1+cosa/2tana/2=1-cosa/sina=sina/1+cosa三角和sinα+β+γ=sinα·cosβ·cosγ+cosα·sinβ·cosγ+cosα·cosβ·sinγ-sinα·sin β·sinγcosα+β+γ=cosα·cosβ·cosγ-cosα·sinβ·sinγ-sinα·cosβ·sinγ-sinα·sin β·cosγtanα+β+γ=tanα+tanβ+tanγ-tanα·tanβ·tanγ/1-tanα·tanβ-tanβ·tanγ-tan γ·tanα两角和差cosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβsinα±β=sinα·cosβ±cosα·sinβtanα+β=tanα+tanβ/1-tanα·tanβtanα-β=tanα-tanβ/1+tanα·tanβ和差化积sinθ+sinφ= 2 sinθ+φ/2 cosθ-φ/2sinθ-sinφ= 2 cosθ+φ/2 sinθ-φ/2cosθ+cosφ= 2 cosθ+φ/2 cosθ-φ/2cosθ-cosφ= -2 sinθ+φ/2 sinθ-φ/2tanA+tanB=sinA+B/cosAcosB=tanA+B1-tanAtanBtanA-tanB=sinA-B/cosAcosB=tanA-B1+tanAtanB积化和差sinαsinβ= cosα-β-cosα+β/2cosαcosβ= cosα+β+cosα-β/2sinαcosβ= sinα+β+sinα-β/2cosαsinβ= sinα+β-sinα-β/2诱导公式sin-α= -sinαcos-α= cosαtan —a=-tanαsinπ/2-α= cosαcosπ/2-α= sinαsinπ/2+α= cosαcosπ/2+α= -sinαsinπ-α= sinαcosπ-α= -cosαsinπ+α= -sinαcosπ+α= -cosαtanA= sinA/cosAtanπ/2＋α＝－cotαtanπ/2－α＝cotαtanπ－α＝－tanαtanπ＋α＝tanα诱导公式记背诀窍：奇变偶不变,符号看象限万能公式sinα=2tanα/2/1+tan＾α/2cosα=1-tan＾α/2/1+tan＾α/2tanα=2tanα/2/1-tan＾α/2其它公式1sinα^2+cosα^2=121+tanα^2=secα^231+cotα^2=cscα^2证明下面两式,只需将一式,左右同除sinα^2,第二个除cosα^2即可4对于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC证:A+B=π-CtanA+B=tanπ-CtanA+tanB/1-tanAtanB=tanπ-tanC/1+tanπtanC整理可得tanA+tanB+tanC=tanAtanBtanC得证同样可以得证,当x+y+z=nπn∈Z时,该关系式也成立由tanA+tanB+tanC=tanAtanBtanC可得出以下结论5cotAcotB+cotAcotC+cotBcotC=16cotA/2+cotB/2+cotC/2=cotA/2cotB/2cotC/27cosA^2+cosB^2+cosC^2=1-2cosAcosBcosC8sinA^2+sinB^2+sinC^2=2+2cosAcosBcosC9sinα+sinα+2π/n+sinα+2π2/n+sinα+2π3/n+……+sinα+2πn-1/n=0cosα+cosα+2π/n+cosα+2π2/n+cosα+2π3/n+……+cosα+2πn-1/n=0 以及sin^2α+sin^2α-2π/3+sin^2α+2π/3=3/2tanAtanBtanA+B+tanA+tanB-tanA+B=0。

中学三角函数公式归纳汇总一、基本关系与公式1. 正弦函数（sin）：- 定义：在直角三角形中，对于角A，正弦函数是对边与斜边的比值，即sinA = 对边/斜边。

- 符号表示：sinA = a/c2. 余弦函数（cos）：- 定义：在直角三角形中，对于角A，余弦函数是邻边与斜边的比值，即cosA = 邻边/斜边。

- 符号表示：cosA = b/c3. 正切函数（tan）：- 定义：在直角三角形中，对于角A，正切函数是对边与邻边的比值，即tanA = 对边/邻边。

- 符号表示：tanA = a/b4. 余切函数（cot）：- 定义：在直角三角形中，对于角A，余切函数是邻边与对边的比值，即cotA = 邻边/对边。

- 符号表示：cotA = b/a5. 正割函数（sec）：- 定义：在直角三角形中，对于角A，正割函数是斜边与邻边的比值，即secA = 斜边/邻边。

- 符号表示：secA = c/b6. 余割函数（csc）：- 定义：在直角三角形中，对于角A，余割函数是斜边与对边的比值，即cscA = 斜边/对边。

- 符号表示：cscA = c/a二、三角函数的特殊角公式1.正弦函数的特殊角公式：- sin0° = 0- sin30° = 1/2- sin45° = √2/2- sin60° = √3/2- sin90° = 12.余弦函数的特殊角公式：- cos0° = 1- cos30° = √3/2- cos45° = √2/2- cos60° = 1/2- cos90° = 03.正切函数的特殊角公式：- tan0° = 0- tan30° = √3/3- tan45° = 1- tan60° = √3- tan90° = 不存在4.余切函数的特殊角公式：- cot0° = 不存在- cot30° = √3- cot45° = 1- cot60° = √3/3- cot90° = 05.正割函数的特殊角公式：- sec0° = 1- sec30° = 2/√3- sec45° = √2- sec60° = 2- sec90° = 不存在6.余割函数的特殊角公式：- csc0° = 不存在- csc30° = 2- csc45° = √2- csc60° = 2/√3- csc90° = 1三、和差公式1.正弦函数的和差公式：- sin(A±B) = sinAcosB ± cosAsinB2.余弦函数的和差公式：- cos(A±B) = cosAcosB ∓ sinAsinB3.正切函数的和差公式：- tan(A±B) = (tanA ± tanB)/(1 ∓ tanAtanB)四、倍角公式1.正弦函数的倍角公式：- sin2A = 2sinAcosA2.余弦函数的倍角公式：- cos2A = cos²A - sin²A = 2cos²A - 1 = 1 - 2sin²A3.正切函数的倍角公式：- tan2A = (2tanA)/(1 - tan²A)五、半角公式1.正弦函数的半角公式：- sin(A/2) = ±√[(1 - cosA)/2]2.余弦函数的半角公式：- cos(A/2) = ±√[(1 + cosA)/2]3.正切函数的半角公式：- tan(A/2) = ±√[(1 - cosA)/(1 + cosA)]这些是中学三角函数的部分公式归纳和汇总，希望对你的学习有所帮助！。

初一数学三角形公式总结归纳常见三角诱导公式公式一：终边相同的角的同一三角函数的值相等设α为任意锐角，弧度制下的角的表示：sin(2kπ+α)=sinα(k∈Z)cos(2kπ+α)=cosα(k∈Z)tan(2kπ+α)=tanα(k∈Z)cot(2kπ+α)=cotα(k∈Z)公式二：π+α的三角函数值与α的三角函数值之间的关系设α为任意角，弧度制下的角的表示：sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三：任意角α与-α的三角函数值之间的关系sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα初中数学三角函数公式大全两角和公式sin(A+B)=sinAcosB+cosAsinBsin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB)tan(A-B)=(tanA-tanB)/(1+tanAtanB)ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA)ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)sin(A/2)=√((1-cosA)/2)sin(A/2)=-√((1-cosA)/2) cos(A/2)=√((1+cosA)/2)cos(A/2)=-√((1+cosA)/2) tan(A/2)=√((1-cosA)/((1+cosA))tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA))ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积公式2sinAcosB=sin(A+B)+sin(A-B)2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B)-2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosBtanA-tanB=sin(A-B)/cosAcosB倍角公式Sin2A=2SinA.CosACos2A=CosA^2-SinA^2=1-2SinA^2=2CosA^2-1 tan2A=(2tanA)/(1-tanA^2)(注：SinA^2是sinA的平方sin2(A))tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA);cot(A/2)=sinA/(1-cosA)=(1+cosA)/sinA.sin^2(a/2)=(1-cos(a))/2cos^2(a/2)=(1+cos(a))/2tan(a/2)=(1-cos(a))/sin(a)=sin(a)/(1+cos(a))积化和差公式sinαsinβ=[cos(α-β)-cos(α+β)]/2cosαcosβ=[cos(α+β)+cos(α-β)]/2sinαcosβ=[sin(α+β)+sin(α-β)]/2万能公式sinα=2tan(α/2)/[1+tan^(α/2)]cosα=[1-tan^(α/2)]/1+tan^(α/2)]tanα=2tan(α/2)/[1-tan^(α/2)]三角形的公式定理1.过两点有且只有一条直线2.两点之间线段最短3.同角或等角的补角相等4.同角或等角的余角相等5.过一点有且只有一条直线和已知直线垂直6.直线外一点与直线上各点连接的所有线段中，垂线段最短7.平行公理经过直线外一点，有且只有一条直线与这条直线平行8.如果两条直线都和第三条直线平行，这两条直线也互相平行9.同位角相等，两直线平行10.内错角相等，两直线平行11.同旁内角互补，两直线平行12.两直线平行，同位角相等13.两直线平行，内错角相等14.两直线平行，同旁内角互补15.定理三角形两边的和大于第三边16.推论三角形两边的差小于第三边17.三角形内角和定理三角形三个内角的和等于180°18.推论1直角三角形的两个锐角互余19.推论2三角形的一个外角等于和它不相邻的两个内角的和20.推论3三角形的一个外角大于任何一个和它不相邻的内角21.全等三角形的对应边、对应角相等22.边角边公理有两边和它们的夹角对应相等的两个三角形全等23.角边角公理有两角和它们的夹边对应相等的两个三角形全等24.推论有两角和其中一角的对边对应相等的两个三角形全等25边边边公理有三边对应相等的两个三角形全等26斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等27.定理1：在角的平分线上的点到这个角的两边的距离相等28.定理2：到一个角的两边的距离相同的点，在这个角的平分线上29.角的平分线是到角的两边距离相等的所有点的集合30.等腰三角形的性质定理等腰三角形的两个底角相等31.推论1：等腰三角形顶角的平分线平分底边并且垂直于底边32.等腰三角形的顶角平分线、底边上的中线和高互相重合33.推论3：等边三角形的各角都相等，并且每一个角都等于60°34等腰三角形的判定定理如果一个三角形有两个角相等，那么这两个角所对的边也相等(等角对等边)35.推论1：三个角都相等的三角形是等边三角形36.推论2：有一个角等于60°的等腰三角形是等边三角形37.在直角三角形中，如果一个锐角等于30°那么它所对的直角边等于斜边的一半38.直角三角形斜边上的中线等于斜边上的一半39.定理线段垂直平分线上的点和这条线段两个端点的距离相等40.逆定理和一条线段两个端点距离相等的点，在这条线段的垂直平分线上41.线段的垂直平分线可看作和线段两端点距离相等的所有点的集合42.定理1关于某条直线对称的两个图形是全等形43.定理2如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线44.定理3两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上45.逆定理如果两个图形的对应点连线被同一条直线垂直平分，那么这两个图形关于这条直线对称46.勾股定理直角三角形两直角边a、b的平方和、等于斜边c的平方，即a+b=c47.勾股定理的逆定理如果三角形的三边长a、b、c有关系a+b=c，那么这个三角形是直角三角形48.定理四边形的内角和等于360°49.四边形的外角和等于360°50.多边形内角和定理n边形的内角的和等于(n-2)×180°51.推论任意多边的外角和等于360°52.平行四边形性质定理1平行四边形的对角相等53.平行四边形性质定理2平行四边形的对边相等54.推论夹在两条平行线间的平行线段相等55.平行四边形性质定理3平行四边形的对角线互相平分56.平行四边形判定定理1两组对角分别相等的四边形是平行四边形57.平行四边形判定定理2两组对边分别相等的四边形是平行四边形58.平行四边形判定定理3对角线互相平分的四边形是平行四边形59.平行四边形判定定理4一组对边平行相等的四边形是平行四边形60.矩形性质定理1矩形的四个角都是直角61.矩形性质定理2矩形的对角线相等62.矩形判定定理1有三个角是直角的四边形是矩形63.矩形判定定理2对角线相等的平行四边形是矩形64.菱形性质定理1菱形的四条边都相等65.菱形性质定理2菱形的对角线互相垂直，并且每一条对角线平分一组对角66.菱形面积=对角线乘积的一半，即S=(a×b)÷267.菱形判定定理1四边都相等的四边形是菱形68.菱形判定定理2对角线互相垂直的平行四边形是菱形69.正方形性质定理1正方形的四个角都是直角，四条边都相等70.正方形性质定理2正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角71.定理1关于中心对称的两个图形是全等的72.定理2关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分73.逆定理如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称74.等腰梯形性质定理等腰梯形在同一底上的两个角相等75.等腰梯形的两条对角线相等76.等腰梯形判定定理在同一底上的两个角相等的梯形是等腰梯形77.对角线相等的梯形是等腰梯形78.平行线等分线段定理如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等79.推论1：经过梯形一腰的中点与底平行的直线，必平分另一腰80.推论2：经过三角形一边的中点与另一边平行的直线，必平分第三边81.三角形中位线定理三角形的中位线平行于第三边，并且等于它的一半82.梯形中位线定理梯形的中位线平行于两底，并且等于两底和的一半L=(a+b)÷2S=L×h83.(1)比例的基本性质如果a:b=c:d,那么ad=bc如果ad=bc,那么a:b=c:d84.(2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d85.(3)等比性质如果a/b=c/d=。

中考生常用三角函数公式1、同角三角函数的差不多关系倒数关系: tan cot＝1 sin csc＝1 cos sec＝1商的关系：sin/cos＝tan＝sec/csc cos/sin＝cot＝csc/sec平方关系：sin^2()＋cos^2()＝1 1＋tan^2()＝sec^2() 1＋cot^2()＝csc^2()平常针对不同条件的常用的两个公式sin +cos =1tan *cot =1一个专门公式（sina+sin）*（sina+sin）=sin（a+）*sin（a-）2、锐角三角函数公式正弦：sin =的对边/ 的斜边余弦：cos =的邻边/的斜边正切：tan =的对边/的邻边余切：cot =的邻边/的对边3、二倍角公式正弦sin2A=2sinAcosA余弦1.Cos2a=Cos^2(a)-Sin^2(a) =2Cos^2(a)-1 =1-2Sin^2(a)2.Cos2a=1-2Sin^2(a)3.Cos2a=2Cos^2(a)-1正切tan2A=（2tanA）/（1-tan^2(A)）4、三倍角公式sin3=4sinsin(/3+)sin(/3-)cos3=4coscos(/3+)cos(/3-)tan3a = tan a tan(/3+a) tan(/3-a)5、n倍角公式sin（n a）=Rsina sin（a+/n）……sin（a+（n-1）/n）。

其中R=2^（n-1）6、半角公式tan(A/2)=(1-cosA)/sinA=sinA/(1+cosA); cot(A/2)=sinA/(1-cosA)=(1+cos A)/sinA. sin^2(a/2)=(1-cos(a))/2 cos^2(a/2)=(1+cos(a))/2 tan(a/2)=(1-cos(a))/s in(a)=sin(a)/(1+cos(a))7、和差化积sin+sin = 2 sin[(+)/2] cos[(-)/2]sin-sin = 2 cos[(+)/2] sin[(-)/2]cos+cos = 2 cos[(+)/2] cos[(-)/2]cos-cos = -2 sin[(+)/2] sin[(-)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)8、两角和公式cos(+)=coscos-sinsincos(-)=coscos+sinsinsin(+)=sincos+cossinsin(-)=sincos -cossin9、积化和差sinsin = [cos(-)-cos(+)] /2 coscos = [cos(+)+cos(-)]/2 sincos = [sin(+) +sin(-)]/2 cossin = [sin(+)-sin(-)]/210、双曲函数sinh(a) = [e^a-e^(-a)]/2 cosh(a) = [e^a+e^(-a)]/2 tanh(a) = sin h(a)/cos h(a)公式一：设为任意角，终边相同的角的同一三角函数的值相等：sin（2 k＋）= sin cos（2k＋）= cos tan（2k＋）= tan cot（2k＋）= cot 公式二：设为任意角，的三角函数值与的三角函数值之间的关系：sin （＋）= -sin cos（＋）= -cos tan（＋）= tan cot（＋）= cot 公式三：任意角与-的三角函数值之间的关系：sin（-）= -sin cos（-）= cos tan（-）= -tan cot（-）= -cot公式四：利用公式二和公式三能够得到与的三角函数值之间的关系：s in（）= sin cos（）= -cos tan（）= -tan cot（）= -cot公式五：利用公式-和公式三能够得到2与的三角函数值之间的关系：s in（2）= -sin cos（2）= cos tan（2）= -tan cot（2）= -cot公式六：/2及3/2与的三角函数值之间的关系：sin（/2+）= cos cos（/ 2+）= -sin tan（/2+）= -cot cot（/2+）= -tan sin（/2-）= cos cos（/2-）=sin tan（/2-）= cot cot（/2-）= tan sin（3/2+）= -cos cos（3/2+）= sin tan（3/2+）= -cot cot（3/2+）= -tan sin（3/2-）= -cos cos（3/2-）= -sin tan（3/2-）= cot cot（3/2-）= tan (以上kZ) Asin(t+)+ Bsin(t+) = {(A +B +2ABcos(-)} sin{ t + arcsin[ (Asin+Bsin) / {A^2 +B^2; +2ABcos(-)} } 表示根号,包括{……}中的内容11、诱导公式sin(-) = -sin cos(-) = cos tan (-)=-tan sin(/2-) = cos cos(/2-) = sin si n(/2+) = cos cos(/2+) = -sin sin() = sin cos() = -cos sin() = -sin cos() = -cos tanA= sinA/cosA tan（/2＋）＝－cot tan（/2－）＝cot tan（－）＝－tan tan（＋）＝tan 诱导公式记背诀窍：奇变偶不变，符号12、万能公式sin=2tan(/2)/[1+(tan(/2))] cos=[1-(tan(/2))]/[1+(tan(/2))] tan=2tan(/2)/[1-(t an(/2))]13、其它公式(1) (sin)+(cos)=1(2)1+(tan)=(sec)(3)1+(cot)=(csc)(4)关于任意非直角三角形,总有tanA+tanB+tanC=tanAtanBtanC (5)cotA cotB+cotAcotC+cotBcotC=1 (6)cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)c ot(C/2)(7)(cosA）+(cosB）+(cosC）=1-2cosAcosBcosC(8)（sinA）+（sinB）+（sinC）=2+2cosAcosBcosC家庭是幼儿语言活动的重要环境，为了与家长配合做好幼儿阅读训练工作，小孩一入园就召开家长会，给家长提出早期抓好幼儿阅读的要求。