《方程的根与函数的零点》导学案

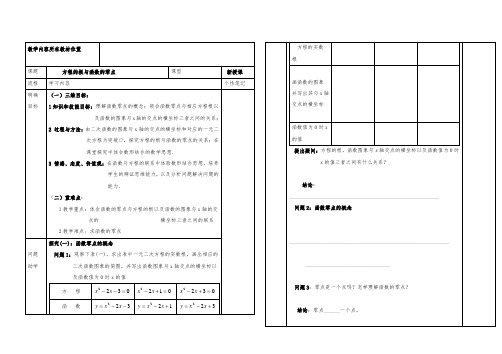
《方程的根与函数的零点》导学案一．学习目标1.结合二次函数的图像，判断一元二次方程根的存在性及根的个数，从而了解函数的零点与方程的根的关系．2.理解并会用函数在某个区间上存在零点的判定方法．二．学习重点、难点重点：了解函数零点的概念，体会方程的根与函数零点之间的联系，掌握函数零点存在性的判断．难点：准确认识零点的概念，能利用判定定理判断零点的存在或确定零点．三．学习过程 （一）课前思考问题1 判断方程2230x x --=根的个数，并求解问题2 作出函数223y x x =--的图象，并思考函数图象与问题1中方程的根有什么联系？思考结论： 问题3 上述关系对于一般的一元二次方程()200ax bx c a ++=≠及其相应的二次函数()20y ax bx c a =++≠是否也成立呢？判别式ac b 42-=∆()200ax bx c a ++=≠的根 ()20y ax bx c a =++≠图象与x轴的交点0>∆0=∆0<∆（二）课堂学习函数零点的定义：______________________________________________________________ ______________________________________________________________例1 求函数)1lg()(-=x x f 的零点．变式练习：求下列函数的零点．（1）65)(2+-=x x x f （2）12)(-=xx f解题小结____________________________________________________________________________________________________________________________________ __________________________________________________________________动手探究：已知函数()y f x =的图象是一条连续不断的曲线，且过点()(),A a f a 、()(),B b f b ，请在下列四个坐标系中分别作出函数()y f x =的一个可能图象．思考：函数满足什么条件，在区间()b a ,上一定有零点？ 探究结论__________________________________________________________________________A ·B ·A ·B ·A ·B ·A ·B ·__________________________________________________________________________ 定理：______________________________________________________________________________________________________________________________________________________________________________________________________________________________反馈练习：1．已知函数()f x 的图象是连续不断的，且有如下对应值表：x1 2 3 4 5 6 ()f x 136.13615.552-3.9210.88-52.488-232.064请写出3个一定存在零点的区间________________________________________________．2．能确定在区间()1,0上有零点的函数是（ ）．A ．()12+=x x fB ．()323+-=x x x fC ．()223-+=x x x fD ．()322++=x x x f3．函数()x f y =在定义域内满足()()()b a R b a b f a f <∈<⋅,,0，则函数()x f 在()b a ,内（ ）A ．只有一个零点B ．至少有一个零点C ．无零点D ．无法确定有无零点 练习心得________________________________________________________________________________________________________________________________________________例2 求函数()ln 26f x x x =+-零点的个数． 归纳总结____________________________________________________________________________________________________________________________________________________________ 反思小结1.你通过本节课的学习，有什么收获？____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________2.对于本节课学习的内容你还有什么疑问？____________________________________________________________________________________________________________________________________________________________________（三）课后作业必做题：《学习与评价》第78页：第10、11题选做题：已知()()221421f x m x mx m =+++-．（1）m 为何值时，函数有两个零点？（2）若函数恰有一个零点在原点右侧，求m 的值．。

《方程的根与函数的零点》导学案一．学习目标1.结合二次函数的图像，判断一元二次方程根的存在性及根的个数，从而了解函数的零点与方程的根的关系．2.理解并会用函数在某个区间上存在零点的判定方法．二．学习重点、难点重点：了解函数零点的概念，体会方程的根与函数零点之间的联系，掌握函数零点存在性的判断．难点：准确认识零点的概念，能利用判定定理判断零点的存在或确定零点．三．学习过程 （一）课前思考问题1 判断方程2230x x --=根的个数，并求解问题2 作出函数223y x x =--的图象，并思考函数图象与问题1中方程的根有什么联系？思考结论： 问题3 上述关系对于一般的一元二次方程()200ax bx c a ++=≠及其相应的二次函数()20y ax bx c a =++≠是否也成立呢？判别式ac b 42-=∆()200ax bx c a ++=≠的根 ()20y ax bx c a =++≠图象与x轴的交点0>∆0=∆0<∆（二）课堂学习函数零点的定义：______________________________________________________________ ______________________________________________________________例1 求函数)1lg()(-=x x f 的零点．变式练习：求下列函数的零点．（1）65)(2+-=x x x f （2）12)(-=xx f解题小结____________________________________________________________________________________________________________________________________ __________________________________________________________________动手探究：已知函数()y f x =的图象是一条连续不断的曲线，且过点()(),A a f a 、()(),B b f b ，请在下列四个坐标系中分别作出函数()y f x =的一个可能图象．思考：函数满足什么条件，在区间()b a ,上一定有零点？ 探究结论__________________________________________________________________________A ·B ·A ·B ·A ·B ·A ·B ·__________________________________________________________________________ 定理：______________________________________________________________________________________________________________________________________________________________________________________________________________________________反馈练习：1．已知函数()f x 的图象是连续不断的，且有如下对应值表：x1 2 3 4 5 6 ()f x 136.13615.552-3.9210.88-52.488-232.064请写出3个一定存在零点的区间________________________________________________．2．能确定在区间()1,0上有零点的函数是（ ）．A ．()12+=x x f B ．()323+-=x x x fC ．()223-+=x x x f D ．()322++=x x x f3．函数()x f y =在定义域内满足()()()b a R b a b f a f <∈<⋅,,0，则函数()x f 在()b a ,内（ ）A ．只有一个零点B ．至少有一个零点C ．无零点D ．无法确定有无零点 练习心得________________________________________________________________________________________________________________________________________________例2 求函数()ln 26f x x x =+-零点的个数． 归纳总结____________________________________________________________________________________________________________________________________________________________ 反思小结1.你通过本节课的学习，有什么收获？____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________2.对于本节课学习的内容你还有什么疑问？____________________________________________________________________________________________________________________________________________________________________（三）课后作业必做题：《学习与评价》第78页：第10、11题选做题：已知()()221421f x m x mx m =+++-．（1）m 为何值时，函数有两个零点？（2）若函数恰有一个零点在原点右侧，求m 的值．。

3.1.1方程的根与函数的零点导学案（2课时）课前预习案【使用说明和学法指导】1、仔细阅读课本，课前完成好预习学案，牢记基础知识，掌握基本题型，时间不超过20分钟。

在做题过程中，如遇不会的问题再回去阅读课本；AA 完成所有题目，BB 完成除★★外所有题目，CC 完成不带★题目。

2、认真限时完成，书写规范；课上小组合作探究，答疑解惑。

3、小组长在课上讨论环节时要在组内起引领作用，控制讨论节奏。

4、必须掌握的数学方法和数学思想：数形结合思想；利用零点的概念、方程的根与函数的零点的关系、零点存有性定理准确处理和解决具体问题。

课前准备：1、课本、《方程的根与函数的零点导学案》、典题本、练习本、双色笔。

2、分析错因，自纠学案。

3、标记疑难，以备讨论。

一．学习目标：1、理解函数的零点概念，理解并掌握函数零点与相对应方程根的联系 。

2、掌握判定函数零点存有的条件，并能确定具体函数存有零点的区间；3、学会将求方程的根的问题转化为求相对应函数零点的问题，转化为求相对应函数的图象与x 轴的交点问题，转化为求两函数图象的交点问题；4、激情投入，高效学习，培养学生形成扎实严谨的科学态度和勇于探索的数学精神。

重点：体会函数的零点与方程的根之间的联系，掌握零点存有的判定条件及应用．难点：探究发现函数零点的存有性.求函数零点的个数、方程根的个数、两函数图象交点的个数问题二．预习导学：自主学习教材P86～P87页内容，思考下列问题，找出疑惑之处。

复习：①函数零点定义：对于函数()y f x =,把使得 的实数x 叫做()y f x =的零点复习：②函数()y f x =有零点的等价条件函数 ()y f x =有零点⇔方程()0f x =有⇔函数()y f x =的图像函数()y f x =的零点⇔方程()0f x =的⇔函数()y f x =的图像复习：③函数零点的求法：代数法、图象法基础落实：④函数零点存有性定理如果函数()y f x =在区间[a,b]上的图象是 的一条曲线，并且有，那么，函数()y f x =在区间（a,b ）内有零点，即存有c ∈（a,b ），使得()0f c =，这个c 也就是方程()0f x =的根三．小试牛刀：（1）函数82xy =-的零点为（2）函数()2x f x x =+ 的一个零点所在的大致区间为（ ）A.（-2，-1）B.（-1，0）C.（0，1）D. （1，2）一、合作探究重点讨论内容：1、零点存有的判定条件；（结合思考1-6及例1）2、函数零点的个数、方程根的个数与两函数图象交点的个数问题的等价转化。

3.1.1方程的根和函数的零点1.理解函数零点的概念，领会函数的零点与相应方程的根的关系，掌握零点存在定理.2.从函数与方程的联系中体会数学中转化思想的意义和方法.3.理性思考、激情投入，体验学习和成功的快乐.重点：零点的定义及零点存在定理；难点：零点存在与否及零点个数的判断.1.结合预习案学习教材86——88页；独立完成探究题，并总结规律方法.2．针对预习自学及探究中找出的疑点，课上小组讨论.3．带有*的为选做.预学案零点的概念：1.函数()y f x=的零点的定义: .2.可以从以下三个方面来理解函数()y f x=的零点（1）函数的零点指的是一个实数，当函数的自变量取这个实数时，其对应的函数值为 .（2）函数的零点可以理解为函数的图象与x轴的交点的 .（3）确定函数()y f x=的零点，就是求方程的 . 3. 函数的零点、方程的根、函数的图象与x轴的交点三者的关系是.我的疑惑。

导学案探究点一函数零点存在性定理1.函数零点存在性定理内容：.2.根据函数零点存在性定理，函数()y f x=满足条件：（1）函数()y f x=在区间[,]a b上的图象是，（2）()()0f a f b⋅<，则函数()y f x=在区间内有零点。

探究点二利用图像求零点例1.求下列函数的零点（1）()23f x x=- (2)2()23f x x x=--(3)2()23f x x x=-+(4) 2()44f x x x=-+方法规律总结：探究点三 零点存在定理例2、（2010天津高考）函数()23x f x x =+的零点所在的一个区间是（ ） A ．（-2，-1） B ．（-1,0） C ．（0,1） D ．（1,2）例3、判断下列函数在给定的区间上是否有零点.（1）()3x f x e x =--在区间[1,2]上.(2)3()35f x x x =--+在区间[0,1]和[1,2]上.变式训练 2()32f x x x =-+在区间[0,3]上.反思与总结固 学 案1. 函数2()76f x x x =-+的零点为（ ） A ．1 B ．6 C ．1 ,6 D ．（1,0），（6,0）2.（2011济南模拟）函数2()23f x x mx =-+有一个零点为12，则(1)f 等于（ ） A ．12-B ．2-C ．0D ．2 3.函数()y f x =在(0,2)上有零点，则（ ）A ．(0)0,(2)0f f ><B ．(0)(2)0f f <C ．在区间(0,2)内存在1x 、2x ，使得12()()0f x f x <D ．以上说法都不正确4、*对于函数2()f x x mx n =++，若()0,()0,f a f b >>则函数()f x 在区间(,)a b 内（ ） A 一定有零点 B 一定没有零点 C 可能有两个零点 D 至多有一个零点5、*已知2()(1)1(0,2)f x x a x =+-+在上有两个零点，求参数a 的取值范围.。

2.4.1方程的根与函数的零点通过本节学习应达到如下目标:1、理解函数（结合二次函数）零点的概念，领会函数零点与相应方程要的关系，掌握零点存在的判定条件．2、通过对零点定义的探究掌握零点存在性的判定方法．3、在函数与方程的联系中体验数学中的转化思想的意义和价值．学习重点：零点的概念及存在性的判定．学习难点：零点的确定．学习过程（一） 自主探究1、 观察下面几个一元二次方程及其相应的二次函数如：方程0322=--x x 与函数322--=x x y方程0122=+-x x 与函数122+-=x x y方程0322=+-x x 与函数322+-=x x y (在下面坐标系中分别做出上述二次函数的图象，并解出的方程根)试说明方程的根与图象与x 轴交点的关系。

(1) (2) (3)2、利用上述关系，试说明一般的一元二次方程)0(02≠=++a c bx ax 的根及其对应的二次函数)0(2≠++=a c bx ax y 的图象有怎样的关系？3、利用以上两个问题的的发现，试总结函数)(x f y =零点的定义，并说明函数)(x f y =的零点，方程0)(=x f 实数根，函数)(x f y =的图象与x 轴交点的横坐标的关系？（二）合作探讨1、（Ⅰ）观察二次函数32)(2--=x x x f 的图象 (见图1) ，完成下面各小题。

1) 在区间]1,2[-上有零点______； =-)2(f _______，=)1(f _______,)2(-f ·)1(f _____0（＜或＞）． 2) 在区间]4,2[上有零点______； )2(f ·)4(f ____0（＜或＞）．（Ⅱ）观察下面函数)(x f y =的图象(如图)，完成下面各小题。

1)在区间],[b a 上______(有/无)零点；)(a f ·)(b f _____0（＜或＞）． 2) 在区间],[c b 上______(有/无)零点；)(b f ·)(c f _____0（＜或＞）． 3) 区间],[d c 上______(有/无)零点；)(c f ·)(d f _____0（＜或＞）． 4) 区间],[d a 上______(有/无)零点；有 个零点；)(a f ·)(d f _____0（＜或＞）． 由以上几步探索，可以得出什么样的结论？2、(根的存在性定理)：在根的存在性定理中只须加入什么条件，零点的个数就是唯一的？3、求函数62ln )(-+=x x x f 的零点个数．(可以借助计算机或计算器来画函数的图象)（三）巩固练习1．利用函数图象判断下列方程有没有根，有几个根：（1）0532=++-x x ； （2）3)2(2-=-x x ；（3）442-=x x ； （4）532522+=+x x x ．2．利用函数的图象，指出下列函数零点所在的大致区间：（1）53)(3+--=x x x f ； （2）3)2ln(2)(--=x x x f ；（3）44)(1-+=-x e x f x ； （4）x x x x x f ++-+=)4)(3)(2(3)(．（四） 能力拓展：设函数12)(+-=ax x f x 。

第三章函数的应用3.1.1 方程的根与函数的零点（导学案）【课时目标】1.理解函数零点的概念以及函数零点与方程根的联系.2.掌握函数零点的存在性定理．3.能够结合二次函数的图象判断一元二次方程根的存在性及根的个数，理解二次函数的图象与x轴的交点和相应的一元二次方程根的关系.【知识梳理】预习课本P86-P881．函数y＝ax2＋bx＋c(a≠0)的图象与x轴的交点和相应的ax2＋bx＋c＝0(a≠0)的根的关系Δ>0 Δ＝0 Δ<02.对于函数y＝f(x)，我们把________________叫做函数y＝f(x)的零点．3．方程、函数、图象之间的关系方程f(x)＝0__________⇔函数y＝f(x)的图象______________⇔函数y ＝f(x)__________．【探究讨论】请观看视频——穿越国门若将中俄两国国界看成x 轴，火车途径的两个站点抽象到平面中来为点A ，B （两点对应的横坐标分别为a,b ），回到函数问题中来，请在下列四个图中分别画出过A ，B 两点的一条连续不断的曲线表示一个函数。

（1） （2）（3） （4）【思考1】满足什么条件，函数()y f x =在区间()b a ,上一定有零点？4．函数零点的存在性定理如果函数y ＝f(x)在区间[a ，b]上的图象是________的一条曲线，并且有____________，那么，函数y ＝f(x)在区间(a ，b)内________，即存在c ∈(a ，b)，使得__________，这个c 也就是方程f(x)＝0的根．【思考2】如果函数有零点，有几个零点？【牛刀小试】()21.log 1f x x =-求函数的零点.()2.23 A.(-2,-1) B.(-1,0) C.(0,1) D.(1,2)x f x x =-函数的零点所在的区间是（ ）3.()35x f x x =+-判断的零点个数.【课后思考】如何求出函数()ln 26f x x x =+-的零点？。

§3.1函数与方程3.1.1方程的根与函数的零点学习目标 1.了解函数的零点、方程的根与图象交点三者之间的联系.2.会借助零点存在性定理判断函数的零点所在的大致区间.3.能借助函数单调性及图象判断零点个数.知识点一函数的零点对于函数y＝f(x)，我们把使f(x)＝0的实数x叫做函数y＝f(x)的零点.方程、函数、图象之间的关系：方程f(x)＝0有实数根⇔函数y＝f(x)的图象与x轴有交点⇔函数y＝f(x)有零点.思考(1)函数的“零点”是一个点吗？(2)函数y＝x2有零点吗？答案(1)不是；(2)有零点，零点为0.知识点二函数的零点、方程的根、函数图象与x轴的交点函数y＝f(x)的零点就是方程f(x)＝0的实数根，也就是函数y＝f(x)的图象与x轴的交点的横坐标，即方程f(x)＝0的实数根⇔函数y＝f(x)的图象与x轴的交点的横坐标⇔函数y＝f(x)的零点. 思考函数f(x)＝ax2＋x－2有一个零点是1，这个函数还有其他零点吗？答案f(x)＝ax2＋x－2有一个零点是1，即a·12＋1－2＝0，∴a＝1，∴f(x)＝x2＋x－2，令x2＋x－2＝0，得x＝1或x＝－2，∴这个函数还有一个零点为－2.知识点三零点存在性定理如果函数y＝f(x)在区间[a，b]上的图象是连续不断的一条曲线，并且有f(a)·f(b)<0，那么，函数y＝f(x)在区间(a，b)内有零点，即存在c∈(a，b)，使得f(c)＝0，这个c也就是方程f(x)＝0的根.1.函数f (x )＝3x －2的零点为23.( √ )2.若f (a )·f (b )>0，则f (x )在[a ，b ]内无零点.( × )3.若f (x )在[a ，b ]上为单调函数，且f (a )·f (b )<0，则f (x )在(a ，b )内有且只有一个零点.( √ )4.若f (x )在(a ，b )内有且只有一个零点，则f (a )·f (b )<0.( × )题型一 求函数的零点例1 (1)函数y ＝1＋1x 的零点是( )A.(－1,0)B.－1C.1D.0 答案 B解析 由1＋1x＝0，得x ＝－1.(2)函数f (x )＝(lg x )2－lg x 的零点为________. 考点 函数零点的概念 题点 求函数的零点 答案 x ＝1或x ＝10解析 由(lg x )2－lg x ＝0，得lg x (lg x －1)＝0， ∴lg x ＝0或lg x ＝1，∴x ＝1或x ＝10.反思感悟 函数y ＝f (x )的零点就是方程f (x )＝0的实数根，也就是函数y ＝f (x )的图象与x 轴交点的横坐标，所以函数的零点是一个数，而不是一个点.在写函数零点时，所写的一定是一个数字，而不是一个坐标.跟踪训练1 (1)函数f (x )＝2x －1－3的零点是______.(2)若函数f (x )＝ax －b (b ≠0)有一个零点3，则函数g (x )＝bx 2＋3ax 的零点是________. 答案 (1)log 26 (2)－1和0解析 (1)解方程2x －1－3＝0，得x ＝log 26，所以函数的零点是log 26. (2)因为f (x )＝ax －b 的零点是3，所以f (3)＝0，即3a －b ＝0，即b ＝3a .所以g (x )＝bx 2＋3ax ＝bx 2＋bx ＝bx (x ＋1)，所以方程g (x )＝0的两个根为－1和0， 即函数g (x )的零点为－1和0.题型二 探求零点所在区间例2 (1)在下列区间中，函数f (x )＝e x ＋4x －3的零点所在的区间为( ) A.⎝⎛⎭⎫－14，0 B.⎝⎛⎭⎫0，14 C.⎝⎛⎭⎫14，12 D.⎝⎛⎭⎫12，34答案 C解析 因为f ⎝⎛⎭⎫14＝4e －2<0，f ⎝⎛⎭⎫12＝e －1>0，所以f ⎝⎛⎭⎫14·f ⎝⎛⎭⎫12<0，又函数f (x )在定义域上单调递增，所以零点在区间⎝⎛⎭⎫14，12上.(2)二次函数f (x )＝ax 2＋bx ＋c 的部分对应值如下表：不求a ，b ，c 的值，判断方程ax 2＋bx ＋c ＝0的两根所在的区间是( ) A.(－3，－1)，(2,4) B.(－3，－1)，(－1,1) C.(－1,1)，(1,2) D.(－∞，－3)，(4，＋∞)答案 A解析 因为f (－3)＝6>0，f (－1)＝－4<0，所以在区间(－3，－1)内必有实数根，又f (2)＝－4<0，f (4)＝6>0，所以在区间(2,4)内必有实数根，故选A.反思感悟 判断单调函数零点所在区间的方法：将区间端点值代入函数解析式求出函数值，进行符号判断即可得出结论，此类问题的难点往往是函数值符号的判断，对此可运用函数的有关性质进行判断.跟踪训练2 根据表格中的数据，可以断定方程e x －(x ＋2)＝0(e ≈2.72)的一个根所在的区间是( )A.(－1,0)B.(0,1)C.(1,2)D.(2,3) 考点 函数零点存在性定理 题点 判断函数零点所在的区间 答案 C解析 令f (x )＝e x －(x ＋2)，则f (－1)≈0.37－1<0，f (0)＝1－2<0，f (1)≈2.72－3<0，f (2)≈7.40－4＝3.40>0.由于f (1)·f (2)<0，∴方程e x －(x ＋2)＝0的一个根在(1,2)内. 题型三 函数零点的个数例3 已知0<a <1，则函数y ＝a |x |－|log a x |的零点的个数为( ) A.1 B.2 C.3 D.4 答案 B解析 函数y ＝a |x |－|log a x |(0<a <1)的零点的个数即方程a |x |＝|log a x |(0<a <1)的根的个数，也就是函数f (x )＝a |x |(0<a <1)与g (x )＝|log a x |(0<a <1)的图象的交点的个数.画出函数f (x )＝a |x |(0<a <1)与g (x )＝|log a x |(0<a <1)的图象，如图所示，观察可得函数f (x )＝a |x |(0<a <1)与g (x )＝|log a x |(0<a <1)的图象的交点的个数为2，从而函数y ＝a |x |－|log a x |的零点的个数为2.延伸探究1.把本例函数“y ＝a |x |－|log a x |”改为“y ＝2x |log a x |－1”，再判断其零点个数.解 由2x |log a x |－1＝0得|log a x |＝⎝⎛⎭⎫12x，作出y ＝⎝⎛⎭⎫12x 及y ＝|log a x |(0<a <1)的图象如图所示.由图可知，两函数的图象有两个交点， 所以函数y ＝2x |log a x |－1有两个零点.2.若把本例条件换成“函数f (x )＝|2x －2|－b 有两个零点”，求实数b 的取值范围. 解 由f (x )＝|2x －2|－b ＝0，得|2x －2|＝b .在同一平面直角坐标系中分别画出y ＝|2x －2|与y ＝b 的图象，如图所示.则当0<b <2时，两函数图象有两个交点，即函数f (x )＝|2x －2|－b 有两个零点.反思感悟 判断函数零点个数的方法主要有：(1)可以利用零点存在性定理来确定零点的存在性，然后借助函数的单调性判断零点的个数.(2)利用函数图象交点的个数判定函数零点的个数.跟踪训练3 求函数f (x )＝ln x ＋2x －6零点的个数. 考点 函数的零点与方程根的关系 题点 判断函数零点的个数解 方法一 由于f (2)＝ln 2＋4－6<0，f (3)＝ln 3＋6－6>0，即f (2)·f (3)<0，又f (x )的图象在(2,3)上是不间断的，所以函数f (x )在区间(2,3)内有零点.又因为函数f (x )在定义域(0，＋∞)内是增函数，所以它仅有一个零点.方法二 通过作出函数y ＝ln x ，y ＝－2x ＋6的图象，观察两图象的交点个数得出结论.也就是将函数f (x )＝ln x ＋2x －6的零点个数转化为函数y ＝ln x 与y ＝－2x ＋6的图象交点的个数. 由图象可知两函数有一个交点，即函数f (x )有一个零点.根据零点情况求参数范围典例 若函数f (x )＝x 2＋2mx ＋2m ＋1在区间(－1,0)和(1,2)内各有一个零点，求实数m 的取值范围.考点 函数的零点与方程根的关系 题点 两根分别属于两区间解 函数f (x )＝x 2＋2mx ＋2m ＋1的零点分别在区间(－1,0)和(1,2)内，即函数f (x )＝x 2＋2mx ＋2m ＋1的图象与x 轴的交点一个在(－1,0)内，一个在(1,2)内，根据图象(图略)列出不等式组⎩⎪⎨⎪⎧f (－1)＝2＞0，f (0)＝2m ＋1＜0，f (1)＝4m ＋2＜0，f (2)＝6m ＋5＞0，解得⎩⎨⎧m ＜－12，m ＞－56，∴－56＜m ＜－12，∴实数m 的取值范围是⎝⎛⎭⎫－56，－12. [素养评析] 函数的零点即函数图象与x 轴交点的横坐标，这样就建立了数与形的联系，利用函数图象描述问题，充分体现直观想象的数学核心素养.1.函数y ＝ln x 的零点是( ) A.(0,0) B.x ＝0 C.x ＝1 D.不存在 考点 函数零点的概念 题点 求函数的零点 答案 C2.下列各图象表示的函数中没有零点的是( )考点 函数零点的概念 题点 判断函数有无零点 答案 D3.函数f (x )＝4x －2x －2的零点是( ) A.(1,0) B.1 C.12 D.－1答案 B4.函数f (x )＝2x －1x的零点所在的区间是( )A.(1，＋∞)B.⎝⎛⎭⎫12，1 C.⎝⎛⎭⎫13，12 D.⎝⎛⎭⎫14，13答案 B5.函数f (x )＝x 3－⎝⎛⎭⎫12x的零点有______个. 考点 函数的零点与方程根的关系 题点 判断函数零点的个数 答案 11.方程f (x )＝g (x )的根是函数f (x )与g (x )的图象交点的横坐标，也是函数y ＝f (x )－g (x )的图象与x 轴交点的横坐标.2.在函数零点存在性定理中，要注意三点：(1)函数是连续的；(2)定理不可逆；(3)至少存在一个零点.3.解决函数的零点存在性问题常用的办法有三种：(1)用定理；(2)解方程；(3)用图象.4.函数与方程有着密切的联系，有些方程问题可以转化为函数问题求解，同样，函数问题有时可以转化为方程问题，这正是函数与方程思想的基础.。

第1课时方程的根与函数的零点1.了解方程的根与函数零点的概念,会利用零点的概念解决简单的问题.2.理解零点存在性定理,会利用零点存在性定理判断零点的存在性或者零点所在的范围.一个小朋友画了两幅图:问题1:上面的两幅图哪一个能说明此小朋友一定曾经渡过河?显然,图1说明了此小朋友曾经渡过河,但对于图2,则无法判断,用数学的角度来看,如果把小朋友运动的轨迹当作函数图象,小河看作x轴,那么问题即转化为函数图象与x轴是否存在交点.问题2:(1)什么是函数的零点,零点是点吗?(2)二次函数的零点个数如何判断?(1)对于函数y=f(x),我们把使的实数x叫作函数y=f(x)的零点.由定义可知零点是一个实数不是点.(2)在二次函数y=ax2+bx+c(a≠0)中,当时,有两个零点;当Δ=0时,有零点;当时,没有零点.问题3:函数y=f(x)的零点,方程f(x)=0的根,函数y=f(x)与x轴交点的横坐标,这三者有什么关系?函数y=f(x)的零点就是方程f(x)=0的实数根,也就是函数y=f(x)的图象与x轴交点的横坐标.事实上,方程f(x)=0有实数根⇔函数y=f(x)的图象与x轴有交点⇔函数y=f(x)有零点.问题4:(1)零点存在性定理的内容是什么?(2)如果函数y=f(x)在区间[a,b]上满足零点存在性定理的条件,即存在零点,那么在(a,b)上到底有几个零点呢?(3)如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,且在区间(a,b)内有零点,那么你认为f(a)·f(b)与0的关系是怎样的?请举例说明.(1)零点存在性定理:如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.(2)至少有一个.(3)如图所示,可以小于0,可以等于0,也可以大于0.1.函数y=x2-2x-3的零点是().A.(-1,0),(3,0)B.x=-1C.x=3D.-1和32.若函数f(x)=x2+2x+a有零点,则实数a的取值范围是().A.a<1B.a>1C.a≤1D.a≥13.观察函数y=f(x)的图象,则f(x)在区间[a,b]上(填“有”或“无”)零点;f(a)·f(b)0(填“<”或“>”),在区间[b,c]上(填“有”或“无”)零点;f(b)·f(c)0(填“<”或“>”),在区间[c,d]上(填“有”或“无”)零点;f(c)·f(d)0(填“<”或“>”).4.已知函数f(x)=2x-x2,问方程f(x)=0在区间[-1,0]内是否有解,为什么?利用零点的概念求零点判断下列函数是否存在零点,如果存在,请求出.(1)f(x)=;(2)f(x)=x2+2x+4;(3)f(x)=2x-3;(4)f(x)=1-log3x.零点个数的判断判断函数f(x)=ln x+x2-3的零点的个数.零点所在区间的判断函数f(x)=lg x-的零点所在的大致区间是().A.(6,7)B.(7,8)C.(8,9)D.(9,10)下列函数中存在两个零点的是().A.f(x)=2x-2B.f(x)=lg(x2-2)C.f(x)=x2-2x+1D.f(x)=e x-1-2判断函数f(x)=x2-的零点的个数.方程2x+x=0在下列哪个区间内有实数根().A.(-2,-1)B.(0,1)C.(1,2)D.(-1,0)1.下列图象表示的函数中没有零点的是().2.已知函数f(x)函数f(x)在区间[1,6]上的零点至少有().A.2个B.3个C.4个D.5个3.函数f(x)为偶函数,其图象与x轴有四个交点,则该函数的所有零点之和为.4.已知函数f(x)=x3-2x2-5x+6的一个零点为1.求函数f(x)的其他零点.(2013年·重庆卷)若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)的两个零点分别位于区间().A.(a,b)和(b,c)内B.(-∞,a)和(a,b)内C.(b,c)和(c,+∞)内D.(-∞,a)和(c,+∞)内考题变式(我来改编):答案第三章函数的应用第1课时方程的根与函数的零点知识体系梳理问题2:(1)f(x)=0(2)Δ>0一个Δ<0问题4:(1)f(a)·f(b)<0基础学习交流1.D由x2-2x-3=0得x=-1或x=3.2.C函数f(x)=x2+2x+a有零点,即方程x2+2x+a=0有实数根,所以Δ=4-4a≥0,得a≤1.3.有< 有< 有< 根据“如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根”来判断.4.解:因为f(-1)=2-1-(-1)2=-<0,f(0)=20-02=1>0,而函数f(x)=2x-x2在[-1,0]上的图象是一条连续曲线,所以f(x)在区间[-1,0]内有零点,即方程f(x)=0在区间[-1,0]内有解.重点难点探究探究一:【解析】(1)令=0,解得x=-3,所以函数f(x)=的零点是-3.(2)令x2+2x+4=0,因为Δ=22-4×1×4=-12<0,所以方程x2+2x+4=0无实数根,所以函数f(x)=x2+2x+4不存在零点.(3)令2x-3=0,解得x=log23,所以函数f(x)=2x-3的零点是log23.(4)令1-log3x=0,解得x=3,所以函数f(x)=1-log3x的零点是3.【小结】求函数f(x)的零点时,通常转化为解方程f(x)=0,若方程f(x)=0有实数根,则函数f(x)存在零点,该方程的根就是函数f(x)的零点;否则,函数f(x)不存在零点.探究二:【解析】(法一)函数对应的方程为ln x+x2-3=0,即为函数y=ln x与y=3-x2的图象交点个数.在同一坐标系下,作出两函数的图象.如图,两函数图象有一个交点.从而ln x+x2-3=0有一个根,即函数y=ln x+x2-3有一个零点.(法二)∵f(1)=ln 1+12-3=-2<0,f(2)=ln 2+22-3=ln 2+1>0,∴f(1)·f(2)<0,又f(x)=ln x+x2-3在(1,2)上是不间断的,∴f(x)在(1,2)上必有零点,又f(x)在(0,+∞)上是递增的,∴零点只有一个.【小结】判断函数零点个数的主要方法:(1)利用方程根,转化为解方程,有几个根就有几个零点;(2)画出函数y=f(x)的图象,判定它与x轴的交点个数,从而判定零点的个数;(3)结合单调性,利用f(a)·f(b)<0,可判定y=f(x)在(a,b)上零点的个数;(4)转化成两个函数图象的交点问题.探究三:【解析】易知f(x)在(0,+∞)上是递增的.∵f(6)=lg 6-=lg 6-<0,f(7)=lg 7-<0,f(8)=lg 8-<0,f(9)=lg 9-1<0,f(10)=lg 10->0,∴f(9)·f(10)<0,∴f(x)=lg x-的零点所在的大致区间为(9,10).【答案】D【小结】判断函数零点所在区间的三个步骤:(1)代:将区间端点代入函数求出函数的值.(2)判:把所得函数值相乘,并进行符号判断.(3)结:若符号为正且函数在该区间内是单调函数,则在该区间内无零点,若符号为负且函数连续,则在该区间内至少有一个零点.思维拓展应用应用一:B A中零点为1;B中零点为±;C中零点为1;D中零点为1+ln 2,故选B.应用二:(法一)由x2-=0,得x2=.令h(x)=x2(x≠0),g(x)=,在同一坐标系中画出h(x)和g(x)的图象,由图可知两函数图象只有一个交点.故函数f(x)=x2-只有一个零点.(法二)当x<0时,f(x)>0恒成立,当x>0时,f(x)是递增的且不间断,又f(1)=1-1=0,故f(x)只有一个零点.应用三:D令f(x)=2x+x,∵f(-1)·f(0)=(-)×1<0,∴f(x)=2x+x的零点在区间(-1,0)内,故2x+x=0在区间(-1,0)内有实数根.基础智能检测1.A观察图象可知A中图象表示的函数没有零点.2.B∵f(2)·f(3)<0,∴f(x)在[2,3]上至少有1个零点,同理f(x)在[3,4]、[4,5]上都存在至少1个零点,∴f(x)在[1,6]上的零点至少有3个,故选B.3.0因为f(x)为偶函数,所以其零点互为相反数,故四个零点之和为0.4.解:由题意,设f(x)=(x-1)(x2+mx+n)=x3+(m-1)x2+(n-m)x-n,则解得令f(x)=0,即(x-1)(x2-x-6)=0⇒(x-1)(x-3)(x+2)=0,解得x=-2,1,3.∴函数f(x)的其他零点是-2,3.全新视角拓展A因为f(a)=(a-b)(a-c)>0,f(b)=(b-c)(b-a)<0,f(c)=(c-a)(c-b)>0,所以f(a)f(b)<0,f(b)f(c)<0,所以函数的两个零点分别在(a,b)和(b,c)内.思维导图构建实数x x轴有零点f(a)·f(b)<0。