当前位置：文档之家 › 建筑力学_结构第四章_应力和强度

建筑力学_结构第四章_应力和强度

  • 格式：ppt
  • 大小：1.73 MB
  • 文档页数：54

下载文档原格式

  / 54

合集下载

杆件的应力与强度—组合变形(建筑力学)

杆件的应力与强度—组合变形(建筑力学)

组合变形
教学目标
知识目标
1.理解组合变形的基本概念； 2.掌握斜弯曲梁的强度计算方法； 3.掌握单向偏心压缩（拉伸）杆件的强度计算方法。
技能目标
1.能够将组合变形问题分解为基本变形的组合； 2.能够对斜弯曲、偏心压缩（拉伸）等组合变形进行强度计算。
重点和难点
重点内容
难点内容
1.组合变形的基本概念；
压缩（拉伸）与弯曲
代入公式得： 解得：h≥280 mm Nhomakorabea此时截面中的最大压应力为：
课程研究内容
1.将组合变形问题分解为基本变形的组合；
2.简单组合变形强度计算方法。 2.应用叠加法解决工程中组合变形实际问题。
组合变形概念 • 组合变形：同时发生两种或两种以上的简单变形。
组合变形实例
组合变形实例
组合变形实例
组合变形实例
组合变形的分析方法
叠加法求解组合变形的计算步骤： （1）将构件的组合变形分解为基本变形； （2）分析、计算构件在每一种基本变形情况下产生的应力； （3）将同一点处的应力进行叠加，计算杆件危险点处的应力，然后进行强 度计算。
（2）内力分析。两个方向弯曲的最大弯矩值都是发生在固定端 截面处，分别为：
My=FL=2×2=4kN.m
斜弯曲
（3）应力分析。由变形情况可知，梁的最大拉应力发生在A点处，梁 的最大压应力发生在B点处，分别为：
故：梁的最大拉应力和最大压应力均为107.73MPa。
压缩（拉伸）与弯曲
l
φ Px 轴向力 ： Px=Pcosφ P 横向力： Py=Psinφ
斜弯曲
斜弯曲
斜弯曲
斜弯曲
【例1】如图所示为一悬臂梁，采用25a号 工字钢，已知q=5kN/m, F=2kN,Wy=48.28cm3,Wz=401.9cm3,求梁 的最大拉应力和最大压应力。
材料力学应力状态和强度理论

材料力学应力状态和强度理论


x 122.5MPa x 64.6MPa
σy 0
τ y 64.6
(122.5 , 64.6)
D1
B2
o
C
B1
(0 , - 64.6)
由 x ， x 定出 D1 点 由 y ， y 定出 D2 点 以 D1D2 为直径作应力圆。
D2
A1，A2 两点的横坐标分别代表 a 点的两个主应力
1 oA1 150MPa
1 x 136.5MPa
σ x 136.5MPa σy 0
τx0 τy0
2 3 0
D2 (0,0)
D1(136.5,0)
x 136.5MPa
b
σ1
σ x 136.5MPa τ x 0
σy 0
τy0
1 所在的主平面就是 x 平面 , 即梁的横截面 C 。
解析法求 a 点的主平面和主应力
解： x 100MPa, y 20MPa, x 40MPa, 300
20
300
100 40
x 100MPa, y 20MPa, x 40MPa, 300
x
2
y
x
2
y
cos
2
x
sin
2
x
2
y
sin
2
x
cos
2
300
100
(20) 2
100
(20) 2
cos( 600)
m
F
A
F
m
A
F
F
A
A 点 横截面 m—m 上的应力为： F
A
n
m
F
A
F
m
n
F
A
2
（完整版）《建筑力学与结构》课程题库试题

（完整版）《建筑力学与结构》课程题库试题

（完整版）《建筑力学与结构》课程题库试题第一章静力学基础一、填空题1、力是。

2、力是矢量，力的三要素分别为：3、刚体是4、所谓平衡，就是指5、力对物体的作用效果一般分效应和效应。

6、二力平衡条件是。

7、加减平衡力系原理是指。

8、力的可传性是。

9、作用于物体上同一点的两个力，可以合成为一个合力，该合力的大小和方向由力的10、平面汇交力系的合力矢量等于，合力在某轴上的投影等于。

11、力矩的大小等于__ ____和__ _______的乘积。

通常规定力使物体绕矩心12、当平面力系可以合成为一个合力时，则其合力对于作用面内任一点之矩，等于力系中各分力对同一点之矩的13、力偶是。

力偶对刚体的作用效应只有。

14、力偶对物体的转动效应取决于、__ __、 ___ _三要素。

15、只要保持力偶的三要素不变，可将力偶移至刚体上的任意位置而不改变其作用效应.16、平面力偶系的合成结果为_ ，合力偶矩的值等于。

17、作用于刚体上的力，均可从_到刚体上任一点，但必须同时在附加一个。

二、判断题：（对的画“√”，错的画“×”）1、两物体间相互作用的力总是同时存在，并且两力等值、反向共线，作用在同一个物体上。

（）2、力的大小等于零或力的作用线通过矩心时，力矩等于零（）3、力偶无合力，且力偶只能用力偶来等效。

（）4、力偶对其作用面内不同点之矩不同。

（）5、分力一定小于合力（）。

6、任意两个力都可以简化为一个合力。

（）7、平面一般力系的合力对作用面内任一点的矩，等于力系各力对同一点的矩的代数和。

（）8、力是滑移矢量，沿其作用线滑移不改变对物体的作用效果。

（）三、计算题1、计算图示结构中力F对O点的力矩2、试计算下图中力对A点之矩四、下列习题中，未画出重力的各物体的自重不计，所有接触面均为光滑接触。

1、试画出下列各物体（不包括销钉与支座）的受力图。

2、如图示，已知F 1=F 2=100N ，F 3=150N ，F 4=200N ，试求其合力。

建筑力学与结构-4 纵向受力构件

建筑力学与结构-4 纵向受力构件


由∑Fy=0： N21－N23sinα－0.5=0
N23=N21-0.5/sinα=3.54（N23为正，表示与图中假设方向一 致）
由∑Fx=0： N23cosα－N24=0
N24=N23cosα=2.5（N24为正，表示与图中假设方向一致， 所以为压力）
由∑Fy=0： N32sinα－N34=0
4.2.1.2 截面形式及尺寸
轴压柱常见截面形式有正方形、矩形、圆形及
多边形。 矩形截面尺寸不宜小于250mm×250mm。为了 避免柱长细比过大，承载力降低过多，常取l0/b≤30， l0/h≤25，b、h分别表示截面的短边和长边，l0表示柱
子的计算长度，它与柱子两端的约束能力大小有关。
4.2.1.3 配筋构造
螺旋箍筋是受力钢筋，这种柱破坏时由于螺旋
箍筋的套箍作用，使得核心混凝土（螺旋筋或焊接 环筋所包围的混凝土）处于三向受压状态，从而间 接提高柱子的承载力。所以螺旋箍筋也称间接钢筋， 螺旋箍筋柱也称间接箍筋柱。螺旋箍筋柱常用的截
面形式为圆形或多边形。
4.2.1 构造要求
4.2.1.1 材料要求
混凝土宜采用C20、C25、C30或更高强度等级。
表4.1 纵向受力构件类型
类别 轴心受力构件（e0=0） 轴心受拉构件 轴心受压构件
简图
变形特
点 举例
只有伸长变形
屋架中受拉杆件、圆形
只有压缩变形
屋架中受压杆等
类别
偏心受力构件(e0≠0)
轴心受拉构件 轴心受压构件
简图 变形特 点 举例 既有伸长变形，又有弯 曲变形 屋架下弦杆（节间有竖 向荷载，主要是钢屋 架）、砌体中的墙梁 既有压缩变形，又有弯曲 变形 框架柱、排架柱、偏心受 压砌体、屋架上弦杆（节 间有竖向荷载）等
电子课件—建筑力学与结构(第三版)—A09-1562 第四章构件的内力、强度和刚度计算课件

电子课件—建筑力学与结构(第三版)—A09-1562 第四章构件的内力、强度和刚度计算课件


（m）或毫米（mm）。
• 线应变:单位长度的变形称为线应变，用ε表示.
l
• ε= l
• 规定拉伸时ε为正，反之为负，线应变无量纲
Logo
2．胡克定律
• 在弹性范围内，杆件的纵向变形与杆件所受的轴
力及杆件长度成正比，与杆件的横截面面积成反比
，这就是胡克定律。 FNL
• Δl = EA
• σ=Eε
（4-3）
• d≥ = 4FN [ ]
470.7103 N =23.02mm，取d=24mm
3.14170MPa
Logo
• ※【例4-6】如图4-18a所示的铰接支架中，杆AC为圆形钢杆
，直径d=10mm，许用应力[σ]=160MPa，横梁BC受到均匀分 布荷载q作用。试根据正应力强度条件确定许用荷载[q]的值。
图4—14 例4—２图
Logo
解：
（1）计算各杆的轴力。如图4-14b所示，取结点B为研究对象 ，杆件轴力均假设为受拉（背离结点）。根据平面汇交力系的平
衡条件得
∑Fy=0：-FNBCsin45°-W=0
FNBC=
-
W sin 45°
=
-
20kN 0.707
= - 28.3kN （压力）
∑Fx=0： -FNBCcos45°-FNBA=0
（4-4）
• 式（4-4）是胡克定律的另一种表达形式。它表明
：在弹性受力范围内，应力与应变成正比。
• E称为材料的弹性模量，与材料的性质有关，单位
为兆帕（MPa）。
Logo
【例4—7】如图4—19所示为一圆形变截面钢杆。各段受力 大 小 及 方 向 如 图 所 示 ， 各 段 横 截 面 面 积 分 别 为 AAB＝ 250 mm2，ABC＝200 mm2，ACD＝150 mm2，各段长度分别为 LAB=1m,LBC=1.5m,LCD=2m,钢的弹性模量E=200 GPa，试 求该杆的总变形。
《建筑力学》高版本 教学课件 建筑力学 第四章(最终)

《建筑力学》高版本 教学课件 建筑力学 第四章(最终)

A M 当角位移 2π 时，则力偶矩 M 在转动一周的角位移上所做的功即为
A M M 2π 若电动机的转速为 n (r/min)，此时角位移 2π n，则力偶矩 M 在一分钟 内的角位移上所做的功为
A M M 2π n
2. 功和功率的关系
电动机的功率有两种单位制：千瓦 (Nk) 和马力 (Np)。 如果输入功率 Nk 为千瓦 (kW)，由于 1 kW 1 kN m/s,1 min 60 s ，则在 1 min 内输入的功为
4.1.1 轴向拉 (压) 变形
图4-1 受力特点：杆件所受外力与杆轴线重合。 变形特点：杆件沿轴线方向伸长或缩短。 产生轴向拉(压)变形的杆件称为拉(压)杆。如图 4-1a 所示，构架中的 AB 杆和 BC 杆分别为拉杆和压杆。
4.1.2 剪切变形
图4-2 受力特点：杆件受一对相距很近、大小相等、方向相反、作用线垂直于 杆轴线的外力 (简称横向力) 的作用。 变形特点：杆件横截面将沿外力方向产生相对错动变形。如图4-2a 所示。 剪切变形的杆件通常为拉 (压) 杆的连接件。例如图4-2b、c 所示的螺栓 连接件的变形均为剪切变形。
③ 平衡求内力：即由静力平衡条件求内力
由
Fx 0
求得
FN F 0
FN F
求得的轴力为正值，表明轴力FN 与假设方向 一致，即为拉力。
若取右半部分为研究对象，如图4-7c 所示，
由
Fx 0
求得
F F'N 0 F 'N F FN
图4-7
上述计算表明：求轴向拉 (压) 杆 m‒m 截面上 的轴力时，不论取 m‒m 截面以左部分杆为研究对象， 还是取 m‒m 截面以右部分杆为研究对象，所求 m‒m 截面上的轴力总是相等的，因为 FN 与 F 'N 是一对作 用力与反作用力的关系。轴力的正、负号规定：轴 力 FN 以拉为正，压为负。
组合变形杆件的强度—斜弯曲梁的应力和强度计算(建筑力学)

组合变形杆件的强度—斜弯曲梁的应力和强度计算(建筑力学)

6
180 120 2 6
mm 3
4.32 105 mm 3
屋面坡度为1：2，则
tan 1 sin 0.4472
2
cos 0.8944
斜弯曲梁的强度计算
（3）强度校核
max
M zmax M ymax
Wz
Wy
M max cos
Wz
M max sin
Wy
cos sin
M max( Wz
A处的正应力为最大拉应力，点C处的正应力为最大压应力：
yA yC ymax
zA zC zmax
max min
t max
cmax
My Iy
zmax
Mz Iz
ymax
My Wy
Mz Wz
M
sin
Wy
cos
Wz
M z 2.51 0.336 2 3.172 kN m M y 1.256 2 2.215 kN m
斜弯曲梁的强度计算
抗弯截面系数为：
Wz
bh2 6
0.6h h2 6
0.1h3
Wy
hb2 6
h (0.6h)2 6
0.06h3
由强度条件：
max
Mz Wz
My Wy
3.172 106 0.1h3
2.512 106 0.06h3
73.587 106 h3
≤[
]
h ≥ 3 73.587 106 194.5(mm) 10
取h = 200mm，b = 120mm。
斜弯曲梁的应力计算 一、斜弯曲的概念
对称截面梁在水平和铅垂两纵向 对称平面内同时承受横向外力的作用， 这时梁分别在水平纵对称面和铅垂纵 对称面内发生对称弯曲，称为斜弯曲 （即为两个相互垂直平面内的弯曲） x
《建筑力学课件-应力状态与应力变化》

《建筑力学课件-应力状态与应力变化》


等效应力的含义
介绍等效应力的概念和在应 力分析中的作用。
等效应力计算方法
讨论不同的计算方法，并重 点介绍单轴拉伸情况下的计 算公式。
等效应力的应用
探讨等效应力在实际建筑结 构中的重要性和应用。
应力状态
1 应力状态的概念
解释应力状态是指材料内部 处于各种应力下的状态。
2 平面应力状态和空间应
力状态
比较平面内的应力状态和立 体内的应力状态的异同。
介绍弹性模量的概念和其在应力变化中 的作用。
随应变弹性模量
了解随应变弹性模量的定义和在结构分 析中的应用。
塑性变形与应力变化特点
1 塑性变形的含义
解释塑性变形是指材料在超过弹性限度后发 生的变形。
2 应力变化的特点
描述塑性变形中应力的变化规律以及其对结 构的影响。
总结
通过这个课件，你已经学会了理解应力状态和应力变化的基本概念，以及它 们在建筑力学中的重要性。掌握这些知识，将有助于你在实际工程中做出准 确的应力分析和设计。
3 均匀分布和不均匀分布
描述应力在结构中的均匀分布和不均匀分布情况。
基本应力状态的描述
拉伸应力
压缩应力
说明拉伸应力的特点和应用领域。
探索压缩应力的特点和在结构中 的应用。
剪切应力
解释剪切应力的本质和结构中的 重要性。
应力变化与弹性模量
1
泊松比的定义

2
探讨泊松比对应力变化的影响和意义。
3
弹性模量的定义
建筑力学课件-应力状态 与应力变化
这个建筑力学课件将向你介绍应力状态和应力变化的重要概念。通过图文并 茂的方式，帮助你全面了解应力及其分类、表达方式，以及应力状态的描述 和变化。
建筑力学课件 应力

建筑力学课件 应力


FN 2 6 .3 × 1 0 3 N 6 = = = 1 3 1 × 1 0 = 1 3 1M P a −3 2 A π × (1 6 × 1 0 ) / 4
例4-4: 已知钢木组合桁架如图，F=16kN, [σ]=120MPa。 试选择钢拉杆D I 的直径。 F F F E F F C A H I D 6×3m=18m 4m B
4 × FN max 4 × 8 ×103 −2 d≥ = = 0.92 × 10 m 6 π [σ ] 3.14 ×120 ×10
取 d=10mm
例4-5: 已知杆AC由两根等边角钢80mm× 80mm × 7mm组成， 杆AB由两根10号工字钢组成, [σ]=170MPa。试求许可载荷[ F ]。
∆P dP p = lim = ∆A→0 ∆A d应力τ
与截面垂直 与截面相切 P2
P1
mτ
p σ P3
P4
m
σ =dN / dA
垂直于截面的正应 力引起材料的分离破坏。 正应力反应内力在截面 上各点拉伸(或压缩)作用 的大小程度。正应力拉 为正，压为负。
τ= dQ / dA
FAy
（1）求支座反力： FAy=40kN; FBy=40kN
FBy
（2）计算DI杆轴力 用截面法，取隔离体： C ΣMA=0, FN2 ×6-F ×3=0 FN2=8kN A FAy （3）设计（最小）截面尺寸：
π d 4
2
F
1
FN1
E 4m FN3
FN2 H
D 2 I 3
=
A
≥
F
[σ ]
N
m a x
1 2
FN1 A FN2 F
由 FNmax≤ A[σ] FN1 ≤ A1[σ] ， 2 F ≤ A1[σ] FN2 ≤ A2[σ] 1.732 F ≤ A2[σ] 所以定义[F1] ，[F2] [ F1]= F ≤ A1[σ] /2=184.6kN [ F2]= F = ≤ A2[σ] /1.732=280.7kN 要同时保证AB、AC杆的强度，应取较小值。结构许可载荷 [F]=min{[ F1], [ F2]}=184.6kN
梁的应力及强度计算—提高梁弯曲强度的措施(建筑力学)

梁的应力及强度计算—提高梁弯曲强度的措施(建筑力学)

提高梁弯曲强度的措施
弯曲正应力是控制梁弯曲强度的主要因素
max
M max Wz
[ ]
设法减小梁内的最大工作正应力，提高梁的承载能力，提高梁的弯曲强度。
1.改善梁的受力情况，以降低最大弯矩Mmax的值； 2.采用合理的截面形状，以提高Wz的数值，使材料得到充分利用。
提高梁弯曲强度的措施
1.降低最大弯矩Mmax的措施 （1）合理布置荷载作用位置及方式
My2
cmax IZ y2 c t max My1 y1 t
IZ
提高梁弯曲强度的措施
3.采用等强度梁（合理设计梁的外形）
在工程实际中，常根据弯矩沿梁轴的变化情况，将梁相应设计成变截面的。 横截面沿梁轴变化的梁，称为变截面梁。
等强度梁——各个横截面具有同样强度的梁。
＝M (x) max W (x)
或
W
(
x)＝
M (x)
（2）采用W/A值大的截面形状 直径为h的圆截面
高为h宽为b的矩形截面
h 3
W 32 h 0.125h
A h 2 8
4
W
1 6
h
0.167h
A bh 6
高为h的槽形或工字形钢截面
W (0.27 ~ 0.31)h A
从正应力的分布规律可知：当距中性轴最远点处应力达到相应许用应力时，
中性轴上或附近的应力分别为零或较小，这部分材料没有充分发挥作用，故应
提高梁弯曲强度的措施
2. 采用合理的截面形状 合理截面形状——指用较少材料获得最大的Wz值。
（1）当截面面积和形状相同时，采用合理的放置方式。
竖放时Wz（b）与横放时Wz（c）比值 因此，矩形截面梁竖放比平放合理。
Wz (b) (bh2 ) /(hb2 ) h 1 Wz (c) 6 6 b
杆件的应力与强度—杆件拉压时应力与强度(建筑力学)

杆件的应力与强度—杆件拉压时应力与强度(建筑力学)


轴向拉（压）杆的强度
2 强度计算
1. 校核强度 2. 设计截面
3. 确定许用载荷
轴向拉（压）杆的强度
【例2】
一直杆AB的受力情况如图（a）所示。直杆的横截面面积A=10 cm2，C点 的拉力为40 kN，D 点拉力为130 kN，材料的许用应力［σ］=160 MPa， 试校核杆的强度。
轴向拉（压）杆的强度
1.轴向拉（压）杆横截面上的应力计算； 2.轴向拉（压）杆的强度计算。
难点内容
1.轴向拉（压）杆件的强度计算； 2.根据已知条件判别轴向拉（压）杆的危险截面。
轴向拉（压）杆截面上的应力
轴向拉（压）杆横截面上应力的分布
轴向拉（压）杆截面上的应力
轴向拉（压）杆横截面上应力的分布特点
轴向拉（压）杆截面上的应力
【例2】 【解】 首先作出直杆AB的轴力图，如图5-27（b）所示。由于是等直杆， CD段的截面是产生最大内力的危险截面，因此由强度条件得：
故满足强度条件。
【例3】
轴向拉（压）杆的强度
图（a）所示为正方形截面阶梯形柱。 已知：材料的许用压应力［σ］=1.05 MPa，弹性模 量 E=3 GPa，荷载FP=60 kN，柱自重不计。试校核 该柱的强度。
轴向拉（压）杆的强度
1 极限应力
2 许应用力 3 安全因数
式中：
—— 许用应力 —— 极限应力 —— 安全因数
对塑性材料一般取：ns=1.4～1.7， 对脆性材料一般取：nb=2.5～5.0。
轴向拉（压）杆的强度
1 强度条件
对于等截面杆件：
式中，Fnmax 和 A 分别为危险截面上的轴力及其横截面面积。
杆件拉压时应力与强度
教学目标
知识目标

建筑力学常见问题解答4杆件的强度、刚度和稳定性计算

建筑力学常见问题解答4 杆件的强度、刚度和稳定性计算1.构件的承载能力，指的是什么？答：构件满足强度、刚度和稳定性要求的能力称为构件的承载能力。

(1)足够的强度。

即要求构件应具有足够的抵抗破坏的能力，在荷载作用下不致于发生破坏。

(2)足够的刚度。

即要求构件应具有足够的抵抗变形的能力，在荷载作用下不致于发生过大的变形而影响使用。

(3)足够的稳定性。

即要求构件应具有保持原有平衡状态的能力，在荷载作用下不致于突然丧失稳定。

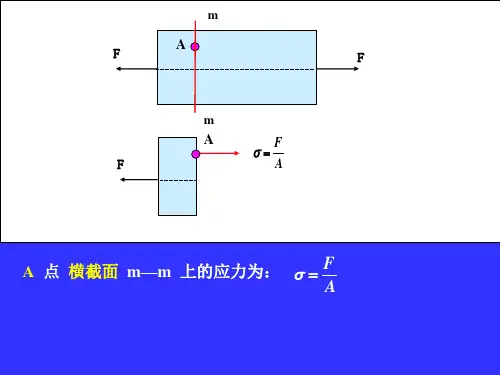
2.什么是应力、正应力、切应力？应力的单位如何表示？答：内力在一点处的集度称为应力。

垂直于截面的应力分量称为正应力或法向应力，用σ表示；相切于截面的应力分量称切应力或切向应力，用τ表示。

应力的单位为Pa。

1 Pa=1 N／m2工程实际中应力数值较大，常用MPa或GPa作单位1 MPa=106Pa1 GPa=109Pa3.应力和内力的关系是什么？答：内力在一点处的集度称为应力。

4.应变和变形有什么不同？答：单位长度上的变形称为应变。

单位纵向长度上的变形称纵向线应变，简称线应变，以ε表示。

单位横向长度上的变形称横向线应变，以ε/表示横向应变。

5.什么是线应变？什么是横向应变？什么是泊松比？答：（1）线应变单位长度上的变形称纵向线应变，简称线应变，以ε表示。

对于轴力为常量的等截面直杆，其纵向变形在杆内分布均匀，故线应变为l l∆=ε（4-2）拉伸时ε为正，压缩时ε为负。

线应变是无量纲（无单位）的量。

（2）横向应变拉(压)杆产生纵向变形时，横向也产生变形。

设杆件变形前的横向尺寸为a，变形后为a1，则横向变形为aaa-=∆1横向应变ε/为aa∆=/ε （4-3） 杆件伸长时，横向减小，ε/为负值；杆件压缩时，横向增大，ε/为正值。

因此，拉(压)杆的线应变ε与横向应变ε/的符号总是相反的。

（3）横向变形系数或泊松比试验证明，当杆件应力不超过某一限度时，横向应变ε/与线应变ε的绝对值之比为一常数。

《建筑力学》第4章计算题知识讲解

《建筑力学》第4章计算题计 算 题( 第四章 )4.1 试作图示各杆的轴力图。

图题4. 14.2 图示等截面混凝土的吊柱和立柱，已知横截面面积A 和长度a ，材料的重度γ，受力如图示，其中10F Aa γ=。

试按两种情况作轴力图，并求各段横截面上的应力，⑴不考虑柱的自重；⑵考虑柱的自重。

图题4.24.3 一起重架由100×100mm2 的木杆BC 和 直径为30mm 的钢拉杆AB 组成，如图所示。

现起吊一重物WF =40kN 。

求杆AB 和BC 中的正应力。

图题4.34.4 图示钢制阶梯形直杆，各段横截面面积分别为21100mm A =，2280mm A =，23120mm A =，钢材的弹性模量GPa E 200=，试求：（1）各段的轴力，指出最大轴力发生在哪一段，最大应力发生在哪一段； （2）计算杆的总变形；图题4.44.5 图示短柱，上段为钢制，长200mm ，截面尺寸为100×100mm2；下段为 铝制，长300mm ，截面尺寸 为200×200mm 2。

当柱顶受F 力作 用时，柱子总长度减少了0.4mm 。

试求F 值。

已知：(E 钢=200GPa ，E 铝=70GPa)。

4.6 图示等直杆AC ，材料的容重为ρg ， 弹性模量为E ，横截面积为A 。

求直杆B 截面的位移ΔB 。

题4.5图 题4.6图4.7 两块钢板用四个铆钉连接，受力kN 4=F 作用，设每个铆钉承担4F 的力，铆钉的直径mm 5=d ，钢板的宽mm 50=b ，厚度mm 1=δ，连接按（a ）、（b ）两种形式进行，试分别作钢板的轴力图，并求最大应力max σ。

题4.7图4.8 用钢索起吊一钢管如图所示，已知钢管重kN10=G F ，钢索的直径mm 40=d ，许用应力[]MPa 10=σ，试校核钢索的强度。

4.9 正方形截面的阶梯混凝土柱受力如图示。

设混凝土的320kN m γ=，载荷kN 100=F ，许用应力[]MPa 2=σ。

《建筑力学》最新备课课件：第四章：四大强度理论


第四章 强度理论
（2）主应力、主平面
y xy
max
x
2
y
(
x
y
)
2
2
xy
2
68.3MPa
x
m in
x
2
y
(
x
y
)2
2
xy
2
48.3MPa
1 68.3MPa, 2 0, 3 48.3MPa
第四章 强度理论
y xy
主平面的方位：
tg20
2 xy x
y
x
60 0.6 60 40
y xy
x
第四章 强度理论
解：（1） 斜面上的应力
y xy
x
y
2
x
y
2
cos 2
xy
sin 2
60 40 60 40 cos(60 ) 30sin(60 )
2
2
x
9.02MPa
x
y
2
sin
2
xy
cos
2
60 40 sin(60 ) 30cos(60 ) 2
58.3MPa
－形状改变比能的极限值，由单拉实验测得
第四章 强度理论
形状改变比能理论（第四强度理论） 屈服条件 强度条件
实验表明：对塑性材料，此理论比第三强度理 论更符合试验结果，在工程中得到了广泛应用。
第四章 强度理论
强度理论的统一表达式： r [ ]
相当应力
r ,1 1 [ ] r,2 1 ( 2 3 ) [ ]
第四章 强度理论
2
1
0 3
2
3
由三向应力圆可以看出：
max

建筑力学第四章_杆件的强度、刚度和稳定性计算


材料的力学性能 工程材料根据其断裂时发生变形的大小 分为脆性材料和塑性材料两大类。在常温、静
载条件下，这两种材料在拉伸和压缩时的力学性能 具有明显的差异。
1）低碳钢拉伸时的力学性能
标准试样（圆截面）
常 温 、 静 载
标准试样（矩形截面） 试样原始标距与原始横截面面积 l0 k A 关系者, 有为比例试样。 国际上使用的比例系数k的值为5.65。 若k 为5.65的值不能符合这一最小标距要求 时，可以采取较高的值（优先采用11.3值）。
zc
C II 3
y
zc
4030 4 cm
5、惯性半径 工程中因为计算需要，常将图形的惯性 矩表示为图形面积A与某一长度平方的乘积。
I y iy A, I z iz A
2
2
即：
iy
Iy A
,
Iz iz A
iy , iz ——惯性半径 （单位：m ）
z dz z
例：1、矩形。求
I y1
II y1
II
3
zc
A AI + AII
zc S y1 A

I II S y1 + S y1
3 20 (-1.5) + 3 17 (-3 - 8.5) AI + AII 3 20 + 3 17 -6.1cm
(2)求 I zc , I yc
1 1 3 I zc I + I 3 20 + 17 33 3 12 12
△A
I
应力表示了受力杆件某截面上一点的内力分 布疏密程度，内力集度.
F1 F2
应力就是单 位面积上的力
Fn
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

§4-2 弯曲时的正应力
变形的几何关系 纵向纤维线应变变化规律: 变形前： a b o 1o 2 d x ab ( y )d 变形后:
o 1o 2 d x d
ab的伸长量：
S ab dx ( y )d d yd
ab的线应变:
3.分别求a、b、c三点正应力
a=MCya/Iz=1MPa(拉) b=MCyb/Iz=0, c=MCyc/Iz=1.5MPa(压)
§4-2 弯曲时的正应力
危险截面: 最大弯矩所在截面 Mmax 横力弯曲时最大正应力 危险点：距中性轴最远边缘点 y max
m ax
M
m ax
y m ax
max
M Wz
W
z
b I
z
h 2

12
h h 2
3

b 6
h
2
§4-3
梁的正应力强度
提高梁弯曲强度的措施
在面积相等的情况下，选择抗弯模量大的截面 z
W
z1

D
32
3
D
a a z
当
D1
4
2
a 时,a
bh 6
2
2
R ; ( D1 / 2 )
3
2
W
z2


(
R)
6
1.18 W
受载后
P
a´ c´
P
平面假设：纵向纤维变形相同，原为平面的横截面在变形后仍为平面。 均匀材料、均匀变形，内力当然均匀分布。 2. 拉伸应力： P

N

N A
轴力引起的正应力 —— ： 在横截面上均布。
三、 强度设计准则（强度条件）：
保证构件不发生强度破坏并有一定安全余量的条件准则。

m ax
正应力公式只能用于发生平面弯曲的梁; 材料处于线弹性范围内; 对于具有一个纵向对称面的梁均适用; 可推广应用于横力弯曲时梁的正应力计算.
§4-2 弯曲时的正应力
纯弯曲理论在横力弯曲中的推广 当L/h≥5时，横截面上的剪力对正应力分布
和最大值的影响一般在5％以内，因此横力弯曲时横 截面上的正应力 采用下式
z1
当
D1
4
2 a1 时 , a1
2
2 D 1
2 a1
z
a1
W z4
bh 6
2

4 a1 6
3
1 . 67 W z 1
工字形截面
§4-3
梁的正应力强度
提高梁弯曲强度的措施
合理安排梁的支座和荷载
目的: 减小梁的最大弯矩 外伸梁和简支梁的比较:
§4-3
梁的正应力强度
提高梁弯曲强度的措施

S dx yd
d

y

§4-2 弯曲时的正应力
• 物理方面(弹性)
E

Ey

静力平衡关系 (合力矩定理、合力定理)
N
M


dA 0
A
y

z d A 0
A
Mz

y d A M
A
Hale Waihona Puke §4-2 弯曲时的正应力 推论1 : 中性轴必通过截面形心 推论2 : z 轴为主惯性轴 正应力计算公式
2
+ M
qL 8
2
x
M
m ax

4050 Nm
q=3.6kN/m
求最大应力并校核强度

max

M
max
Wz

6M bh
max 2

6 4050 0 . 12 0 . 18 [ ]
2
qL 2
V
6.25MPa
7MPa
+
–
2
x
qL
m ax 1 . 5
V m ax A

矩形截面梁
剪应力分布假设 横截面上的剪应力都平行于剪 力V 剪应力沿截面宽度均匀分布， 与中性轴等距处大小相等
§4-4
梁的剪应力强度
矩形截面梁剪应力计算公式

dM S z
*
dx I zb

QSz I zb
*
Q—横截面上剪力； Iz—整个横截面对中性轴的惯性矩； b — 所求剪应力处的截面宽度； Sz*—所求剪应力处横线一侧部分面积A*对中性轴静矩
W
z

I
z
h 2

12

b 6
h
2
W
z

I d
z

64 d
d
4
Wz
I
z
D 2

64
(D
4
d )
4
D 2 d D


32
d
3
2
2


32
D [1 (
3
) ]
4
§4-3
梁的正应力强度
正应力强度条件
m ax
M
m ax
WZ
[ ]
[]— 材料的容许应力
矩形和工字形截面梁正应力
lim
Δ N dN dA Δ A0 Δ A
p

M

位于截面内的应力称为“剪应力”(Shearing Stress)。
lim
ΔA0
ΔV ΔA
2

dV dA
应力的单位： N/m
即 帕斯卡 Pa
1GPa =103MPa =109Pa
二、拉（压）杆横截面上的应力 1. 变形规律试验及平面假设： 变形前 a c b d b´ d´ 横截面
矩形(bh=0.12m0.18m）截面木梁
如图，[]=7MPa，[]=0. 9 M Pa， 试求最大正应力和最大剪应力之比 ,并校核梁的强度。 –
2
L=3m
qL 2
+
x
qL
解：画内力图求危险截面内力
qL 2
qL 8
V max

2
3600 3 2
3600 3 8
5400 N
σ
x

M(x)y I z
§4-2 弯曲时的正应力
示例： 矩形截面悬臂梁受均布荷载q=2kN/m, b=120mm, h=180mm,L=2m.求C截面a、b、c正应力 1.C截面上弯矩
MC=-q×L/2 ×L/4=-qL2/8=-1kN· m
2.矩形截面惯性矩
Iz=bh3/12=0.583×10-4 m4
铆接或焊接的组合截面，其腹板的厚度与高度比小于型钢的
1 . 5 5400 0 . 12 0 . 18 0.9MPa [ ]
0.375MPa
+ M
qL 8
2
x
应力之比

m ax
m ax

M
m ax
2A 3Q
Wz

L h
16 . 7
§4-3
梁的正应力强度
提高梁弯曲强度的措施
采用合理截面形状
原则：当面积A一定时,尽可能 增大截面的高度,并将较多的材 料布置在远离中性轴的地方,以 得到较大的抗弯截面模量。
c)
中
性
z m
梁横截面上的变形 规律：
（1）纵向线a-a和b-b， 由变形前的直线变成 了平行的圆弧线，凹 边的纵向线缩短，凸 边纵向线伸长。 （2）在变形前，与梁轴 线垂直的横向直线mm和n-n变形后仍保持 为直线，相互倾斜了 一个角度，但仍与弯 曲后的梁轴线保持垂 直。
m
中性层
层
x
O y
d)
m
Iz
令Iz /ymax=Wz ,则max=Mmax/Wz Wz —抗弯截面模量
矩形截面:Wz=bh2/6, Wy=hb2/6 圆形截面:Wz= Wy= D3/32 正方形截面:Wz= Wy= a3/6
一、极惯性矩： 定义：平面图形中任一微面积dA与它到坐 标原点Ｏ的距离ρ平方的乘积ρ2dA,称为该面积 dA对于坐标原点o的极惯性矩。
§4-2 弯曲时的正应力
梁横截面上正应力的最大值：
永远出现在梁截面的上、下边缘处

m ax

t m ax

c m ax

My I
m ax z
令Wz
Iz y m ax
——抗弯截面模量
M Wz
则

max

t max
c max
§4-2 弯曲时的正应力
正应力公式的使用条件及推广
Q m ax S z I zb



[] —材料弯曲时容许剪应力
§4-4
梁的剪应力强度
设计梁时必须同时满足正应力和剪应力的强度条件。对 细长梁，弯曲正应力强度条件是主要的，一般按正应力强度 条件设计，不需要校核剪应力强度，只有在个别特殊情况下 才需要校核剪应力强度。 需要校核剪应力的几种特殊情况： 梁的跨度较短，M 较小，而V较大时，要校核剪应力。
截面对坐标原点o的极惯性矩为：
IP
§4-3
截面的几何特征

A
dA ;
2
简单图形的极惯性矩可由定义式积分计算。
D
实心圆截面： 空心圆截面：
IP
IP

2
0
2 dA
4 4
2
D
32 d
D
4
;
)