键的强度计算

平键联接的强度计算
平键联接传递转矩时，联接中各零件的受力如图所示。

对于采用常见的材料组合和按标准选取尺寸的普通平键联接，其主要失效是工作面被压溃，而一般不会出现键的剪断。

因此，通常只按工作面上的挤压应力进行强度校核计算。

对于导向键联接和滑键联接，其主要失效形式是工作面的过度磨损。

因此，通常按工作面上的压力进行条件性的强度校核计算。

假定载荷在键的工作面上均匀分布，普通平键联接的强度条件为：
导向平键联接和滑键联接的强度条件为：
式中：
T－传递的转矩（T=F×y≈F×d/2），单位为N·m；
k－键与轮毂键槽的接触高度，k=0.5h，h为键的高度，单位为mm；
l－键的工作长度，圆头平键l=L-b，平头平键l=L，单圆头平键l=L-b/2，L为键的长度，b为键的
宽度，单位均为mm；
d－轴的直径，单位为mm；
[σp]－键、轴、轮毂三者中最弱材料的许用挤压应力，单位为MPa；
[p] －键、轴、轮毂三者中最弱材料的许用压力，单位为MPa；
在进行强度计算校核后，如果强度不够，可采用双键联接。

这时一方面应考虑键的合理布置，即两个平键最好布置在沿周向相隔180°；另一方面,应考虑两个键上载荷分配的不均匀性，在进一步的强度校
核中只按1.5个键计算。

化学键的强度和键长计算化学键是由原子之间的电荷云重叠形成的强相互作用力，它是物质中最基本的连接方式。

化学键的强度和键长是两个重要的物理参数，对于理解分子结构和化学反应机理有着重要的意义。

本文将介绍如何计算化学键的强度和键长。

一、离子键的强度和键长计算离子键是由金属与非金属之间的电荷转移形成的键。

其强度和键长的计算可以通过库仑定律来实现。

库仑定律表达了两个带电粒子之间相互作用力的大小与它们之间距离的平方成反比关系。

若两个离子之间的电荷分别为q1和q2，它们之间的距离为r，那么它们之间的作用力F可以通过下式计算：F = k * q1 * q2 / r^2其中，k是库仑常数，其数值为8.9875×10^9 N·m^2/C^2。

由于离子键中离子具有完全转移电荷的特点，因此离子键的键长可以通过原子半径之和来近似计算，即：r = r1 + r2其中，r1和r2分别是两个离子的半径。

二、共价键的强度和键长计算共价键是由两个非金属原子之间的电子共享形成的键。

其强度可以通过化学键能来进行计算。

化学键能是指在气体状态下，将1摩尔分子中的键断裂所需要吸收的能量。

假设共价键中的两个原子之间的距离为r，那么化学键能E可以通过下式计算：E = -A / r^n + B / r^m其中，A、B、n和m是与具体共价键有关的参数。

它们的数值将取决于共价键中的原子种类和电子数。

共价键的键长可以通过最小化化学键能来计算。

即找到使化学键能达到最小值的键长r0，即：dE/dr = 0通过求解上述方程，即可得到共价键的键长r0。

三、其他键的强度和键长计算除了离子键和共价键，还存在其他类型的键，如金属键和氢键。

金属键是由金属原子之间形成的键，而氢键是由氢原子与其他原子之间形成的键。

它们的强度和键长的计算方法与离子键和共价键略有不同。

金属键的强度可以通过Hume-Rothery规则来大致估计。

该规则基于金属晶体中的电子云重叠程度来计算金属键的强度。

返回目录
项目
公式
单位
结果
传递功率P kW 2转速n
r/min 60输入转矩T=9549*P/n N.m 318.3平均圆直径dm
mm 30名义切向力Ft=2000*T/dm N
21220键齿数N 6键长l
mm 50单位载荷
W=Ft/（N*l）
N/mm 70.73333333
工作齿高h W =h min
mm 4齿面压应力σH =W/h w <[σH ]MPa 17.68333333
材料的屈服强度σ0.2
MPa
340齿面接触强度的安全系数S H =1.25～1.52使用系数K 1
1齿侧间隙系数K 2=1.1～2.0 1.5分配系数K 3 1.2轴向偏载系数
K 4
1
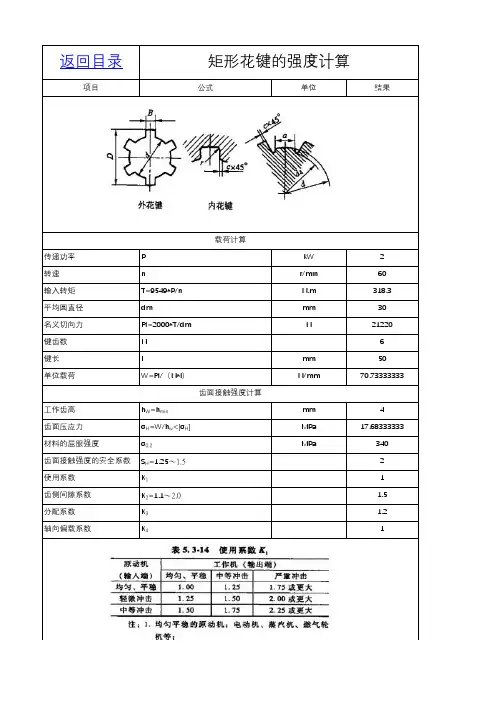
矩形花键的强度计算
载荷计算
齿面接触强度计算
齿面许用压应力[σH]=σ0.2/（S H*K1*K2*K3*K4）MPa94.44444444
齿根抗弯强度计算
齿全高h5
齿根危险截面的弦齿厚S Fn 4.5
齿根弯曲应力σF=6*h*W/S Fn^2<[σF]104.7901235抗弯强度计算的安全系数S F=1.25～22
齿面的许用弯曲应力[σF]=σb/（S F*K1*K2*K3*K4）MPa94.44444444材料的抗拉强度σb MPa340
齿根抗剪强度计算
齿根最大扭转切应力τFmax=τm*αm<[τF]
花键收尾处的切应力τm=16000*T/Pi/dh^3。

化学键的强度和键长计算案例分析化学键是化学反应的基础，它决定了分子的稳定性和性质。

本文将通过案例分析化学键的强度和键长的计算方法，帮助读者更好地理解这一概念。

1. 引言化学键是原子之间电子的共享或转移所形成的力，它能够将原子牢固地连接在一起。

化学键的强度和键长是描述两个原子之间相互作用程度的重要指标。

2. 强度计算化学键的强度可以通过键能计算。

键能是指在分子中解离1摩尔该化学键所需要吸收的能量。

常见的计算键能的方法有两种：实验测量和计算模拟。

2.1 实验测量法实验测量法是通过实验手段来确定键能。

一种常见的方法是利用光谱技术，如红外光谱或拉曼光谱，观察分子中键振动所对应的频率，再通过实验数据和相关的计算公式，可以计算出键能值。

2.2 计算模拟法计算模拟法是通过计算机程序对化学键进行模拟和计算，得到键能的近似值。

这种方法适用于计算简单分子的键能，常用的计算方法有量子力学计算和分子力学计算。

3. 键长计算键长是指两个原子之间的距离。

在计算键长时，一般采用实验测量和理论计算两种方法。

3.1 实验测量法实验测量法是通过实验手段来确定键长。

一种常用的方法是X射线晶体学，通过晶体结构的分析，可以得到分子中化学键的准确长度。

3.2 理论计算法理论计算法是通过计算模拟来预测键长。

分子力学计算是其中较常用的方法，通过构建分子模型、考虑分子的力场和相互作用力，利用计算机对分子的结构进行模拟和计算，得到键长的近似值。

4. 案例分析以氢氧化钠（NaOH）分子为例，分析其化学键的强度和键长。

4.1 强度计算利用计算模拟法，采用量子力学计算方法，可以得到Na-O键的键能为X kJ/mol。

4.2 键长计算利用理论计算法，通过分子力学计算，可以预测Na-O键的键长为X Å。

5. 结论通过案例分析，我们可以看到计算模拟是一种有效的方法来计算化学键的强度和键长。

然而，实验测量仍然是确保准确性的主要手段。

我们需要综合利用实验测量和计算模拟的结果来获得更准确的化学键信息。

化学键的强度与键能计算方法化学键是指由原子间的电子转移或共享而形成的化学连接。

它的强度和键能是评估一种化学键稳定性的重要指标。

本文将介绍化学键的强度与键能计算方法，并探讨其在化学研究中的应用。

一、化学键的强度化学键的强度是指键在受外界作用下能够抵抗断裂的能力。

化学键的强度与键能密切相关，其取决于键的类型和原子之间的相互作用力。

1. 离子键的强度离子键是通过电子转移形成的化学键。

离子键的强度主要取决于离子的电荷大小和离子半径。

通常情况下，同等价数的阳离子和阴离子之间形成的离子键强度较大。

2. 共价键的强度共价键是通过电子共享形成的化学键。

共价键的强度与其键长和键级有关。

一般来说，键长越短、键级越高的共价键强度越大。

3. 金属键的强度金属键是由金属原子形成的化学键。

金属键的强度取决于金属原子的密排程度、电子海模型以及原子间的电子云重叠程度。

金属键一般具有较高的强度。

二、键能的计算方法键能是指在克服化学键吸引力时需要释放的能量。

由于化学键的形成和断裂通常涉及到大量的原子和分子，实验测量键能相对复杂。

因此，理论计算方法成为研究键能的重要手段。

1. 密度泛函理论(DFT)密度泛函理论是一种基于量子力学的计算方法，通过对电子的运动轨迹进行求解，进而计算化学键的键能。

DFT方法可以根据分子的几何结构和电子密度来计算键能，精度较高。

2. 分子动力学模拟(MD)分子动力学模拟是一种基于牛顿力学的计算方法，通过模拟分子与分子之间的相互作用，推导出键能。

MD方法可以根据分子的动力学行为模拟化学键的断裂过程，对键能进行计算。

3. 经验估算法经验估算法基于实验数据和已有的化学规律，通过建立统计模型来估算化学键的键能。

常用的经验估算法有Mulliken等离子体模型、Clementi-Raimondi规则等。

三、应用与展望化学键的强度和键能计算方法在化学研究中具有广泛的应用。

它们可以用于研究分子的稳定性、反应动力学以及材料的力学特性等。

化学物质化学键强度练习题键能与键长的计算化学物质化学键强度练习题：键能与键长的计算化学键是化学物质中连接原子的力，它决定了物质的性质和反应能力。

化学键的强度可以通过键能和键长来计算和描述。

本文将介绍一些与化学键强度相关的练习题，并探讨如何计算键能和键长。

1. 某化合物的键长为1.2埃，键能为400 kJ/mol。

请计算该键的强度。

为计算键的强度，我们可以使用以下公式：键强度 = 键能 / 键长根据给定的数据，我们可以进行计算：键强度= 400 kJ/mol / 1.2 Å ≈ 333 kJ/mol·Å所以，该键的强度为333 kJ/mol·Å。

2. 某分子的键长为1.4埃，键强度为250 kJ/mol·Å。

请计算该键的键能。

键能 = 键强度 ×键长根据给定的数据，我们可以进行计算：键能= 250 kJ/mol·Å × 1.4 Å ≈ 350 kJ/mol所以，该键的键能为350 kJ/mol。

通过上述两个例子，我们可以看出键能和键长是化学键强度的两个关键因素。

键能是指在断裂一组键时需要吸收或释放的能量，而键长则表示两个原子之间的距离。

除了通过实验测定外，我们还可以通过理论方法来估算键能和键长。

其中一种常用的方法是量子力学计算，例如密度泛函理论(DFT)和分子力场方法。

这些方法可以基于原子的电子结构和相互作用来预测键的强度。

化学键的强度对于理解物质的性质、反应机理以及材料设计具有重要意义。

例如，酸碱中和反应中的键强度和键长变化将直接影响反应速率和平衡。

此外，通过调整键强度和键长，可以增强材料的力学性能、电子传导性能等。

总结起来，键能和键长是衡量化学键强度的重要指标。

通过实验或理论计算，我们可以准确地确定键能和键长的数值。

这些数据有助于我们了解物质的性质、反应机理，并指导材料设计与合成。

键连接的选择和计算1．键的选择I 轴齿轮1处选择普通平头平键键128,12,8,40b mm h mm L mm ⨯===；联轴器处选择普通平头平键键87,8,7,32b mm h mm L mm ⨯===；II 轴齿轮2处选择普通平头平键键149,14,9,36b mm h mm L mm ⨯===；齿轮3处选择普通平头平键键149,14,9,70b mm h mm L mm ⨯===；III 轴齿轮4处选择普通平头平键键2012,20,12,70b mm h mm L mm ⨯===；联轴器处选择普通平头平键键1610,16,10,70b mm h mm L mm ⨯===；2．键的强度计算假定载荷在键的工作面上均匀分布，普通平键联接的强度条件为3210[]P P T kldσσ⨯=≤ 查表6-2得，钢材料在轻微冲击下的许用挤压应力为100~120MPa ，所以取 []120P MPa σ=(1) I 轴齿轮1上键的强度计算1111170.180.50.58440T N mk h mm l L mm=⋅==⨯===所以 122[]44040P P MPa σσ==≤⨯⨯ 满足强度条件I 轴联轴器上键的强度计算1111170.180.50.57 3.532T N mk h mm l L mm=⋅==⨯===所以 31270.181050[]3.53225P P MPa σσ⨯⨯==≤⨯⨯ 满足强度条件(2). II 轴上齿轮2处键的强度计算22222317.70.50.59 4.536T N mk h mm l L mm=⋅==⨯===所以 322317.71087[]4.53645P P MPa σσ⨯⨯==≤⨯⨯ 满足强度条件 II 轴上齿轮3处键的强度计算22222317.70.50.59 4.570T N mk h mm l L mm=⋅==⨯===所以 322317.71045[]4.57045P P MPa σσ⨯⨯==≤⨯⨯ 满足强度条件(3) III 轴齿轮4处键的强度计算 3333310250.50.512670T N mk h mm l L mm=⋅==⨯===所以 369.7[]67070P P MPa σσ==≤⨯⨯ 满足强度条件 联轴器处键的强度计算3333310250.50.510570T N mk h mm l L mm=⋅==⨯===所以 332102510106[]57055P P MPa σσ⨯⨯==≤⨯⨯ 满足强度条件。

化学键的强度与解离能的计算化学键是指由原子间相互作用形成的连接力，它决定了分子的性质和反应能力。

化学键的强度与解离能密切相关，本文将介绍化学键的强度与解离能的计算方法。

一、离子键的强度与解离能的计算离子键是由正、负电荷离子之间的静电吸引力形成的化学键。

它的强度与解离能可以通过库仑定律进行计算。

库仑定律表示两个电荷之间的相互作用力与电荷的乘积成正比，与它们之间的距离的平方成反比。

假设有两个离子，一个正电荷为q1，另一个负电荷为q2，它们之间的距离为r，则它们之间的电荷相互作用力F可以表示为：F = k * |q1 * q2| / r^2其中，k为比例常数，可以用来表示各种物理常数。

离子键的强度与解离能可以通过计算电荷相互作用力来确定。

二、共价键的强度与解离能的计算共价键是由原子间电子的共享形成的化学键。

它的强度与解离能可以通过化学键的键能来计算。

键能是指在形成化学键时释放的或吸收的能量。

一般来说，键能可以通过反应焓的变化来计算。

假设有一个反应X + Y -> XY，其中X和Y为反应物，XY为产物。

它们之间的键能可以表示为：E = ΔH / n其中，ΔH为反应焓的变化，n为键的个数。

通过测定反应焓的变化，可以计算出键的强度与解离能。

三、金属键的强度与解离能的计算金属键是由金属原子之间的金属键相互作用形成的化学键。

金属键的强度与解离能可以通过金属原子之间的离子半径和电子密度来计算。

一般来说，金属键的强度与解离能与金属离子的半径成反比。

金属离子的半径越小，金属键的强度与解离能越大。

此外，金属离子的电子密度越高，金属键的强度与解离能也越大。

因此，金属键的强度与解离能可以通过测定金属离子的半径和电子密度来计算。

综上所述，化学键的强度与解离能可以通过不同的计算方法来确定。

离子键的强度与解离能可以使用库仑定律计算，共价键的强度与解离能可以通过反应焓的变化确定，金属键的强度与解离能可以通过金属离子的半径和电子密度来计算。

化学中的键长与化学键的强度关系化学键是由原子之间的电子云的相互作用形成的，它们在化学反应中扮演着重要的角色。

化学键的强度与键长之间存在着紧密的关系。

本文将探讨化学中的键长与化学键的强度之间的关系。

首先，我们来了解一下化学键的定义。

化学键是指两个原子之间因电子云的相互作用而形成的连接。

化学键的形成是原子之间共享电子对或通过电子的转移实现的。

根据共享的电子对数目可以将化学键分为单键、双键、三键等。

化学键的强度与键长之间的关系可用弗鲁克公式来描述，即F=k(Q1Q2/r^2)，其中F表示化学键的力矩，k为一个比例常数，Q1和Q2分别为两个相互作用的原子的电荷，r为原子间距。

从弗鲁克公式可以看出，原子间的距离r对化学键的强度有着直接的影响。

当两个原子的距离增加时，化学键的强度减弱，反之亦然。

这是因为原子之间的距离增加会导致相互作用的电子云的重叠减少，从而减弱了化学键的强度。

此外，化学键的强度还与原子的电荷有关。

电荷的多少决定了电子云的分布和电云的相互吸引力。

当原子的电荷增加时，化学键的强度也会增加。

因此，原子的电荷与化学键的强度呈正相关关系。

除了键长和原子电荷，其他因素也会对化学键的强度产生影响，如两个原子的原子半径、原子核的电荷和电子的云密度分布等。

这些因素的综合作用会影响化学键的强度。

需要注意的是，虽然键长与化学键的强度之间存在着关系，但并不是所有情况下键长的增加都会导致化学键的强度减弱。

在某些情况下，增大键长可能会导致一种新的键型的形成，从而增强了化学键的强度。

总结起来，化学中的键长与化学键的强度之间存在着密切的关系。

原子间的距离越大，化学键的强度越小；原子的电荷越大，化学键的强度越大。

此外，其他因素如原子半径、电子云密度分布等也会对化学键的强度产生影响。

通过对这些因素的理解，我们可以更好地认识和理解化学键在化学反应中的作用。

化学键的强度与键能的计算公式化学键是连接原子的力，其强度与键能密切相关。

本文将讨论化学键的强度与计算键能的公式。

首先，我们需要了解化学键以及其相关的概念和定义。

1. 化学键的定义与概念在化学中，原子通过化学键结合在一起形成分子或化合物。

化学键可以分为共价键、离子键和金属键等不同类型。

- 共价键：共用一对电子，通常形成于非金属之间。

它是一种相对较强的化学键，能够通过共享电子而形成分子。

- 离子键：由正负离子吸引力形成，常见于金属与非金属之间的化合物。

离子键通常较强，但也易于解离。

- 金属键：金属中的离子通过自由电子形成，共享电子云。

金属键通常较强，但较为弹性。

2. 化学键的强度与键能化学键的强度与键能的概念存在着密切的联系。

化学键的强度指的是键在受到外力作用下的抗拉能力，是一种物理性质。

而键能是产生和断裂化学键所需要的能量，是一种热力学性质。

3. 强度与键能的关系化学键的强度与键能之间存在一定的关系，但并不完全一致。

键能是评估键的稳定性和化学反应的重要指标，而强度则更多地反映了键在外力作用下的稳定程度。

化学键的强度与键能可通过以下公式计算：强度 = 断裂能 / 断面积其中，断裂能是指断裂一个单位长度的键所需要的能量，单位通常为焦耳/摩尔。

断面积则指单位长度断裂后键的切面面积。

键能可通过以下公式计算：键能 = 断裂能 ×键长度这个公式是基于键能是断裂能与断开键的长度之积的计算。

在实际应用中，我们可以利用各种实验和计算方法来测定化学键的强度和键能。

例如，拉伸实验可以通过在一个小样品上施加外力，使其断裂，并根据断裂过程中释放出的能量来计算键能。

总结：化学键的强度与键能密切相关，但并不完全一致。

化学键的强度反映了键在外力作用下的稳定程度，而键能则是评估键的稳定性和化学反应的重要指标。

强度与键能可以通过相关公式进行计算，从而在理论上或实验上评估化学键的特性。

随着科学技术的不断发展，人们对化学键的了解也在不断深入。

化学键的强度与键能的计算化学键是化学反应中形成的化合物中两个原子之间的力。

化学键的强度和稳定性对于理解化学反应和物质性质非常重要。

本文将介绍化学键的强度和键能的计算方法。

一、化学键的强度化学键的强度是指在断裂该化学键时所需的能量。

通常，化学键的强度可以通过测量断裂化学键所需的能量来确定。

下面介绍几种常见的化学键和它们的强度。

1. 离子键离子键是由正负离子之间的静电引力所形成的化学键。

离子键的强度取决于离子间的电荷和离子间的距离。

通常，开尔文（kJ/mol）是度量化学键强度的常用单位。

2. 共价键共价键是由两个非金属原子之间共享电子形成的化学键。

共价键的强度取决于键的长度、键的角度以及原子之间的电负性差异。

一般来说，共价键的强度介于离子键和金属键之间。

3. 金属键金属键是由金属原子间的金属键合形成的。

金属键的强度取决于金属离子的电子云的排列规律。

金属键是一种相对较弱的化学键。

二、键能的计算键能是指形成一个化学键时释放或吸收的能量。

可以通过计算化学反应的焓变来确定键能。

以下是一些计算键能的常用方法。

1. 离子键能的计算离子键能可以通过计算离子化反应的焓变来估算。

离子键能的计算公式如下：离子键能 = 晶体离子的总电荷 ×离子间距离 / 2其中，离子键能的单位是焦耳（J）。

2. 共价键能的计算共价键能可以通过计算化学反应的焓变来估算。

共价键能的计算公式如下：共价键能 = 共价键的键级 × 348 / 2其中，共价键能的单位是千焦耳（kJ/mol），348是CO键的键能。

3. 化学键能的估算化学键能可以通过实验或理论计算来获得。

实验方法包括热化学分析、热量计量等。

理论计算方法则利用量子力学和分子力学手段进行计算。

结论化学键的强度对于理解化学反应和物质性质起着至关重要的作用。

离子键、共价键和金属键是常见的化学键类型，它们的强度取决于离子间电荷、距离、共享电子数量以及原子的排列规律。

键能可以通过计算化学反应的焓变来估算，离子键能和共价键能的计算公式分别为离子键能=晶体离子的总电荷×离子间距离/2以及共价键能=共价键的键级×348/2。

化学键的强度与键能的计算化学键是物质中原子之间的相互作用力，它的强度决定了物质的性质和化学反应的进行。

而化学键的强度又可以通过键能来进行计算。

一、化学键的强度化学键的强度是指抵抗外部力破坏的能力，直接影响物质的稳定性和化学性质。

化学键的强度与键的种类和键的长度有关。

1. 金属键的强度金属键是金属内部形成的一种化学键，金属键的强度比较高。

这是因为金属元素的价电子比较少，形成的金属键中电子云能够自由移动，形成电子海模型，使金属具有良好的导电性和热导性。

2. 共价键的强度共价键是非金属元素之间形成的化学键，共价键的强度比金属键略弱。

共价键的强度与键的长度有关，共价键较短的分子通常比较稳定。

3. 离子键的强度离子键是由阳离子和阴离子之间形成的化学键，离子键的强度介于金属键和共价键之间。

离子键的强度取决于离子的电荷量和离子的半径。

二、键能的计算键能是指在断裂一个化学键时所需施加的能量。

通过计算键能可以了解化学键的强度。

1. 共价键的键能计算共价键的键能可以通过简化的形式来进行计算，例如可以使用伯特兰方程（Berthelot equation）或者通过对称性因子（symmetry factor）进行近似计算。

这些方法可以用来估计共价键的键能。

2. 金属键的键能计算金属键的键能可以通过比较不同金属的晶体结构和含有金属键的化合物的性质来进行估计。

实验技术如X射线衍射可以提供关于晶体结构的信息，从而推导出金属键的键能。

3. 离子键的键能计算离子键的键能可以通过离子热动力学数据来计算。

通过测量离子热（lattice energy）和晶体结构信息，可以估计离子键的键能。

总结：化学键的强度直接影响物质的性质和化学反应的进行。

金属键常具有较高的强度，而共价键和离子键的强度与键的长度、电荷量、半径等因素有关。

通过计算键能可以了解化学键的强度。

不同类型的键有不同的计算方法，如共价键的计算可以使用伯特兰方程或对称性因子进行估计，金属键的计算可以通过比较晶体结构和化合物的性质，离子键可以通过测量离子热和晶体结构信息来计算。

化学键的强度和键能的计算和比较化学键是物质中原子之间的相互作用力，它决定了物质的性质和反应能力。

在化学中，我们常常需要计算和比较不同化学键的强度和键能。

本文将探讨化学键强度和键能的计算方法，并比较不同类型化学键的特点。

一、离子键的强度和键能计算离子键是由离子之间的静电相互作用形成的。

其强度和键能可以通过库仑定律进行计算。

库仑定律描述了两个电荷之间的相互作用力与它们之间距离的关系。

对于离子键，库仑定律可以表示为：F = k * (q1 * q2) / r^2其中，F为相互作用力，k为比例常数，q1和q2为两个离子的电荷量，r为两个离子之间的距离。

根据库仑定律，离子键的强度和键能与离子电荷量的乘积成正比，与离子间距离的平方成反比。

二、共价键的强度和键能计算共价键是由原子之间的电子共享形成的。

其强度和键能可以通过分子轨道理论和量子力学计算。

分子轨道理论认为，共价键可以看作是原子轨道的线性组合形成的分子轨道。

通过求解分子轨道的波函数，可以得到共价键的能量。

量子力学计算可以通过求解薛定谔方程来获得共价键的波函数和能量。

薛定谔方程描述了分子中电子的运动状态。

通过数值方法或近似方法，可以求解薛定谔方程，得到共价键的能量。

三、金属键的强度和键能计算金属键是由金属原子之间的金属键形成的。

其强度和键能可以通过密堆积模型和电子气模型进行计算。

密堆积模型认为，金属原子在晶体中紧密堆积，形成金属键。

通过计算金属原子的配位数和密堆积度，可以估算金属键的强度。

电子气模型认为，金属中的自由电子形成了电子气，与金属正离子形成金属键。

通过计算金属中自由电子的密度和电子云的能量，可以得到金属键的强度和键能。

四、比较不同类型化学键的特点离子键具有较高的强度和键能，因为离子之间的静电相互作用力较强。

离子键的特点是电子转移，形成带电离子。

离子键在晶体中形成离子晶体，具有高熔点和脆性。

共价键具有中等的强度和键能，因为原子之间的电子共享较弱。

化学中的键长与化学键的强度关系化学键是由原子之间的电子云的相互作用形成的，它们在化学反应中扮演着重要的角色。

化学键的强度与键长之间存在着紧密的关系。

本文将探讨化学中的键长与化学键的强度之间的关系。

首先，我们来了解一下化学键的定义。

化学键是指两个原子之间因电子云的相互作用而形成的连接。

化学键的形成是原子之间共享电子对或通过电子的转移实现的。

根据共享的电子对数目可以将化学键分为单键、双键、三键等。

化学键的强度与键长之间的关系可用弗鲁克公式来描述，即F=k(Q1Q2/r^2)，其中F表示化学键的力矩，k为一个比例常数，Q1和Q2分别为两个相互作用的原子的电荷，r为原子间距。

从弗鲁克公式可以看出，原子间的距离r对化学键的强度有着直接的影响。

当两个原子的距离增加时，化学键的强度减弱，反之亦然。

这是因为原子之间的距离增加会导致相互作用的电子云的重叠减少，从而减弱了化学键的强度。

此外，化学键的强度还与原子的电荷有关。

电荷的多少决定了电子云的分布和电云的相互吸引力。

当原子的电荷增加时，化学键的强度也会增加。

因此，原子的电荷与化学键的强度呈正相关关系。

除了键长和原子电荷，其他因素也会对化学键的强度产生影响，如两个原子的原子半径、原子核的电荷和电子的云密度分布等。

这些因素的综合作用会影响化学键的强度。

需要注意的是，虽然键长与化学键的强度之间存在着关系，但并不是所有情况下键长的增加都会导致化学键的强度减弱。

在某些情况下，增大键长可能会导致一种新的键型的形成，从而增强了化学键的强度。

总结起来，化学中的键长与化学键的强度之间存在着密切的关系。

原子间的距离越大，化学键的强度越小；原子的电荷越大，化学键的强度越大。

此外，其他因素如原子半径、电子云密度分布等也会对化学键的强度产生影响。

通过对这些因素的理解，我们可以更好地认识和理解化学键在化学反应中的作用。

化学键的键能计算在化学中，化学键是连接原子的力，它们是物质结构和性质的基础。

而键能则是描述化学键的强度的物理量。

本文将介绍化学键的键能计算方法。

一、电负性差值法电负性差值法是一种常用的计算化学键能的方法。

根据元素的电负性值，可以推测某个化学键是否是离子键、极性共价键还是非极性共价键。

1. 离子键的键能计算离子键是由电子的转移而形成的化学键。

它的键能可以通过用下式计算得到：E = k * (|q1 * q2|) / d其中，E表示键能，k表示库仑常数，q1和q2分别表示连结原子中的电荷数，d表示两个原子之间的距离。

这个计算方法基于库仑定律，可以比较准确地计算离子键的键能。

2. 极性共价键的键能计算极性共价键是由两种非金属元素组成的化学键。

它的键能可以通过用下式计算得到：E = k * ((q1 * q2) / d^2) * (1 - cosθ)其中，E表示键能，k表示库仑常数，q1和q2分别表示连结原子中的偏离电荷数，d表示两个原子之间的距离，θ表示键的夹角。

这个计算方法考虑了键的极性和角度的影响。

3. 非极性共价键的键能计算非极性共价键是由两种相同或相似的非金属元素组成的化学键。

它的键能可以通过用下式计算得到：E = k * ((q1 * q2) / d^2)其中，E表示键能，k表示库仑常数，q1和q2分别表示连结原子中的偏离电荷数，d表示两个原子之间的距离。

这个计算方法忽略了键的极性和角度的影响。

二、轨道重叠法轨道重叠法是另一种计算化学键能的方法，它基于两原子轨道的重叠程度来估算键的强度。

根据轨道理论，分子的键能可以通过以下公式计算：E = S * (H11 + H22 - 2H12)其中，E表示键能，S表示轨道重叠积分，H11和H22分别表示孤立原子轨道的哈密顿量，H12表示两个原子轨道之间的相互作用哈密顿量。

三、实验测定法除了理论计算方法，实验测定法也是一种常用的计算化学键能的方式。

通过测量物质在化学反应中的能量变化，可以推断出化学键的强度。