高二数学线面距离和面面距离的求法

立体几何中空间距离的求法
立体几何中空间距离的求法
443711 湖北省兴山一中 万忠国
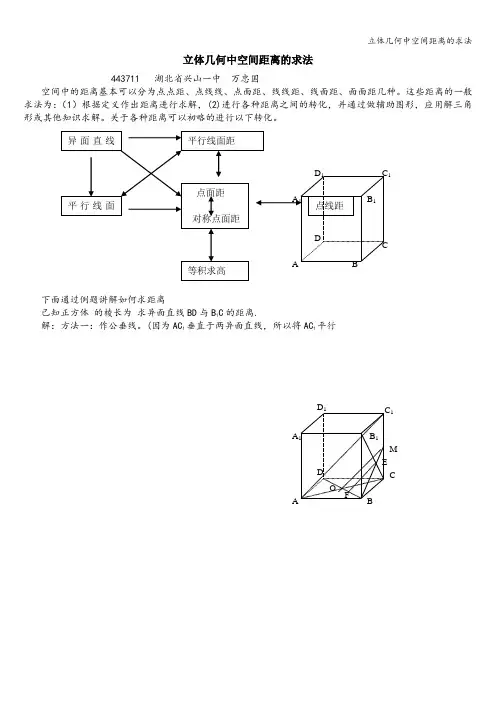
空间中的距离基本可以分为点点距、点线线、点面距、线线距、线面距、面面距几种。

这些距离的一般求法为：（1）根据定义作出距离进行求解，(2)进行各种距离之间的转化，并通过做辅助图形，应用解三角形或其他知识求解。

关于各种距离可以初略的进行以下转化。

下面通过例题讲解如何求距离
已知正方体 的棱长为 求异面直线BD 与B 1C 的距离.
解：方法一：作公垂线。

(因为AC 1垂直于两异面直线，所以将AC 1平行
1 A
B 1
B
D 1
C
D A 1
C 1
E
O
M F。

两个面的距离公式
一、空间中两个平行平面的距离公式。

（一）定义。

1. 在空间中，如果两个平面α∥β，那么这两个平面间的距离就是在其中一个平面α上任取一点P，点P到另一个平面β的距离。

（二）公式推导。

1. 设平面α的法向量为→n=(A,B,C)，P(x_0,y_0,z_0)是平面α上一点，平面β的方程为Ax + By+ Cz+D = 0。

- 根据点到平面的距离公式d=frac{|
Ax_0+By_0+Cz_0+D|}{√(A^2)+B^{2+C^2}}。

- 因为P(x_0,y_0,z_0)在平面α上，设平面α的方程为Ax + By + Cz+D_1=0，则Ax_0+By_0+Cz_0+D_1 = 0，即Ax_0+By_0+Cz_0=-D_1。

- 那么平面α与平面β（Ax + By+ Cz+D = 0）的距离d=frac{| D -
D_1|}{√(A^2)+B^{2+C^2}}。

二、空间中异面直线间的距离公式。

（一）定义。

1. 异面直线a，b的公垂线段的长度称为异面直线a，b的距离。

（二）公式推导（向量法）
1. 设异面直线a，b的方向向量分别为→m，→n，A，B分别是直线a，b上的点。

- 向量→AB，则异面直线a，b的距离
d=frac{|(→m×→n)·→AB|}{|→m×→n|}。

- 这里→m×→n是→m和→n的向量积，其模|→m×→n|=|→m||→n|sinθ（θ为→m与→n的夹角），(→m×→n)·→AB是向量(→m×→n)与→AB的数量积。

高中数学线面距离方法汇总全文共四篇示例，供读者参考第一篇示例：高中数学中，线面距离是一个重要的概念，涉及到线和平面之间的最短距离。

在解决数学问题时，线面距离方法可以帮助我们快速准确地求解各种题目。

今天我们就来总结一下高中数学中常见的线面距离方法。

一、直线和平面的距离1. 点到平面的距离公式设平面方程为Ax+By+Cz+D=0，点P(x0,y0,z0)在平面上，则点P到平面的距离为：d = |Ax0+By0+Cz0+D| / √(A²+B²+C²)其中(a,b,c)为直线上的一点。

3. 平行线面距离如果直线l平行于平面Π，直线和平面之间的距离为两者所含向量的点积模的比值，也就是直线上的一点到平面的距离就是这一点到平面上任意一点的距离。

二、两平面之间的距离如果两个平面Π1和Π2的法向量分别为n1和n2，平面到平面的距离为：d = |d|sinθd是两平面之间的距离，θ是n1和n2的夹角。

如果两个平行的平面Π1: Ax+By+Cz+D1=0和Π2:Ax+By+Cz+D2=0，它们的距离为：三、点到线的距离设线段两端点为A和B，点P到线段的距离为点P到直线AB的距离，如果点P在直线AB的延长线上，则点P到线段的距离等于点P到端点A或B的距离。

设两条线段AB和CD，线段到线段的最短距离取决于它们的垂直距离，并且有可能在端点处取得最小值。

我们可以通过求解两线段组成的四边形的四边长度来求解线段到线段的最短距离。

通过以上总结，我们可以看到，在高中数学中，线面距离方法应用广泛，涉及到点、线、面之间的距离。

在解决数学问题时，我们可以根据具体情况选择合适的方法，通过计算距离来求解各种问题。

希望本文对大家在学习数学时有所帮助。

【字数：583字】第二篇示例：高中数学中，线面距离方法是指计算线段与平面之间的距离的一种数学方法。

在几何学中，线段与平面之间的距离是一种重要的概念，它在实际问题中经常被用到，比如在建筑设计中确定物体之间的距离，或者在物理学中计算物体移动的距离等。

平面距离公式平面距离公式是描述平面上两点之间的距离的数学公式。

在平面几何中，我们经常需要计算两点之间的距离，这在实际生活中有很多应用，比如测量距离、导航等。

下面将介绍平面距离公式及其应用。

平面距离公式的一般形式为：d = √((x2-x1)² + (y2-y1)²)，其中(x1, y1)和(x2, y2)分别表示平面上的两个点的坐标，d表示两点之间的距离。

这个公式的原理是根据勾股定理，将两点之间的直线距离转化为坐标差的平方和的平方根。

通过这个公式，我们可以方便地计算平面上任意两点之间的距离。

在实际应用中，平面距离公式有很多用途。

首先，它可以用于测量平面上的实际距离。

比如在建筑工程中，我们需要测量两个建筑物之间的距离，可以通过测量它们的坐标，然后利用平面距离公式计算出实际距离。

平面距离公式也可以用于导航系统中。

在现代社会中，人们经常使用导航软件来指导驾驶或步行。

导航系统会根据起点和终点的坐标，利用平面距离公式计算出最短路径，并给出相应的导航指示。

平面距离公式还可以用于地理信息系统（GIS）中。

GIS是一种用来收集、管理、分析和展示地理信息的系统。

在GIS中，平面距离公式可以用来计算地图上两个点之间的距离，从而实现地理数据的分析和可视化。

除了上述应用外，平面距离公式还可以用于计算机图形学、物理学、经济学等领域。

在计算机图形学中，平面距离公式可以用来计算图像上两个像素点之间的距离，从而实现图像处理和计算机视觉任务。

在物理学中，平面距离公式可以用来计算物体的运动轨迹和速度。

在经济学中，平面距离公式可以用来计算两个城市之间的距离，从而分析贸易和交通网络。

平面距离公式是一种非常重要的数学工具，它可以用来计算平面上任意两点之间的距离。

通过应用平面距离公式，我们可以解决很多实际问题，包括测量距离、导航、地理信息分析等。

希望通过本文的介绍，读者对平面距离公式有更深入的了解，并能在实际应用中灵活运用。

高中数学“线面距离”典例剖析线面距离典例剖析【例1】求证：如果一个平面经过一条线段的中点，那么这条线段的两个端点到这个平面的距离相等.已知：线段AB的中点为O，O∈平面α.求证：A、B两点到平面α的距离相等.证明：(1)当线段在平面α上时，A、B两点显然到平面α的距离相等且为0.(2)当线段AB不在平面α上时，作AA1⊥α，BB1⊥α，A1和B1为垂足，则AA1、BB1分别是A、B到平面α的距离，且AA1∥BB1，AA1、BB1确定平面β，β∩α=A1B1.∵O∈AB，ABβ，∴O∈β，又O∈α.∴O∈A1B1.∴AA1&perp ;A1O，BB1⊥B1O.∵∠AOA1=∠BOB1，AO=BO，∴Rt△AA1O≌Rt△BB1O.∴AA1=BB1，即线段AB的两个端点到平面α的距离相等.点评：该题中，证明A1、O、B1三点共线是关键，离开这一点，就无法证明三角形全等.另外，第(1)步有些同学往往漏掉，使证明失掉严谨性.【例2】如图，已知AB是异面直线A、B的公垂线段，Bα，a∥α，求证：线段AB的长就是a与平面α之间的距离.证明：∵Ba，∴由直线a、点B可确定平面，设为β，则α和β相交，设=a′.∵a∥α，&the re4;a∥a′.又∵AB⊥a，∴AB⊥a′.∵a、b是异面直线，∴b∩a′=B.又b、a′α，∴AB⊥α，a∈a，A∥α.∴AB的长为a到α之间的距离.点评：由本例的结论知异面直线a、b之间的距离(公垂线段AB的长度)就是a与α之间的距离，利用这个结论，求异面直线间的距离可转化为求线面之间的距离.【例3】如图，已知梯形ABCD的一底边AB在平面α内，另一底边DC在平面α外，对角线交点O到平面α的距离为d，若AB∶CD=m∶n，求CD到平面α的距离.解：∵CD在平面α外，CD∥BA，BAα，∴CD∥平面α.作CC1⊥α，C1为垂足，则CC1就是CD和平面α的距离.作OO1⊥AC1于O1，∵CC1⊥AC1，∴OO1∥CC1.∵CC1⊥α，∴OO1⊥α.∴OO1是O到平面α的距离，即OO1=d.在梯形ABCD中，==，∴=.在平面ACC1内，==，∴CC1=d.因此，CD到平面α的距离为d.点评：求线面之间的距离，“作、证、算”三步必不可少，即找出代表距离的垂线段并证明之，然后构造平面图形(多数为三角形)来算出.归根结底求解它们都可以和直线与平面垂直建立密切的联系。

向量法求直线到面的距离公式
直线到面的距离是指，在几何空间中，一条直线和一个面的距离。

这里，直线和面之间的距离，可以通过向量法来求解。

首先，我们使用向量法来求解直线到面的距离，需要用到两个向量：一个是直线向量，表示直线在空间中的方向；另一个是面法向量，表示面在空间中的方向。

其次，通过以上两个向量求解直线到面的距离，我们可以使用以下公式：
距离 = |直线向量 X 面法向量| / |面法向量|
其中，| |表示向量的模，这个公式表示直线到面的距离就是直线向量和面法向量的叉乘，除以面法向量的模。

最后，向量法求解直线到面的距离在几何学中是一个重要的概念，它可以用来解决许多实际问题，如机械结构中的接触力分析等。

总之，要求解直线到面的距离，可以使用向量法，公式为：距离= |直线向量 X 面法向量| / |面法向量|。

空间距离的常用求法策略内蒙古科技大学附属中学 申炎 （014030）本文主要介绍高中阶段在立体几何中求解空间距离的一些常用方法，这些方法包括了点面距离，线面距离，面面距离以及异面直线距离求解的常用方法，其中包含近年来的高考题真题，并为这些题目提供了一些新的解法。

一 直接法直接利用点到面的距离，线面距离，两平行平面的距离以及两异面直线的距离的定义来计算求解。

例1(2008年重庆文 20)如图,α和β为平面，l αβ=，A α∈，B β∈，5AB =，A ，B 在棱l上的射影分别为A '，B '，3AA '=，2BB '=。

若二面角l αβ--的大小为32π，求：点B 到平面α的距离。

解：如图，过点'B 作直线//B C AA ''且使B C AA ''=。

过点B 作BD CB '⊥，交CB '的延长线于D 。

由已知AA l '⊥，可得DB l '⊥，又已知BB l '⊥，故l⊥平面BB D '，得BD l ⊥。

又因BD CB '⊥，从而BD α⊥平面，BD 之长即为点B 到平面α的距离。

因B C l '⊥且BB l '⊥，故BB C '∠为二面角l αβ--的平面角。

由题意，BB C '∠=32π,因此在RT BB D '中，2BB '=，BB D '∠ =π-BB C '∠=3π，BD =sin BB BB D ''∠ =3。

点评：在直接法作点到平面的距离时，要注意确定垂足的位置，以便于计算。

C1CA1AB例2（2008年重庆理19）如图,在ABC 中，2B π∠=，152AC =，D 、E 两点分别在AB 、AC 上，使2AD AEDB EC==，3DE =。

现将ABC 沿DE 折成直二面角，求：异面直线AD 与BC 的距离。

1.直线在平面内的判定(1)利用公理1：一直线上不重合的两点在平面内，则这条直线在平面内.(2)若两个平面互相垂直，则经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内，即若,A，AB，则AB.(3)过一点和一条已知直线垂直的所有直线，都在过此点而垂直于已知直线的平面内，即若Aa,ab，A,b，则a.(4)过平面外一点和该平面平行的直线，都在过此点而与该平面平行的平面内，即若P，P，∥，Pa,a∥，则a.(5)如果一条直线与一个平面平行，那么过这个平面内一点与这条直线平行的直线必在这个平面内，即若a∥,A，Ab,b∥a,则b.2.存在性和唯一性定理(1)过直线外一点与这条直线平行的直线有且只有一条;(2)过一点与已知平面垂直的直线有且只有一条;(3)过平面外一点与这个平面平行的平面有且只有一个;(4)与两条异面直线都垂直相交的直线有且只有一条;(5)过一点与已知直线垂直的平面有且只有一个;(6)过平面的一条斜线且与该平面垂直的平面有且只有一个;(7)过两条异面直线中的一条而与另一条平行的平面有且只有一个;(8)过两条互相垂直的异面直线中的一条而与另一条垂直的平面有且只有一个.3.射影及有关性质(1)点在平面上的射影自一点向平面引垂线，垂足叫做这点在这个平面上的射影，点的射影还是点.(2)直线在平面上的射影自直线上的两个点向平面引垂线，过两垂足的直线叫做直线在这平面上的射影.和射影面垂直的直线的射影是一个点;不与射影面垂直的直线的射影是一条直线.(3)图形在平面上的射影一个平面图形上所有的点在一个平面上的射影的集合叫做这个平面图形在该平面上的射影.当图形所在平面与射影面垂直时，射影是一条线段;当图形所在平面不与射影面垂直时，射影仍是一个图形.(4)射影的有关性质从平面外一点向这个平面所引的垂线段和斜线段中：(i)射影相等的两条斜线段相等，射影较长的斜线段也较长;(ii)相等的斜线段的射影相等，较长的斜线段的射影也较长;(iii)垂线段比任何一条斜线段都短.4.空间中的各种角等角定理及其推论定理若一个角的两边和另一个角的两边分别平行，并且方向相同，则这两个角相等.推论若两条相交直线和另两条相交直线分别平行，则这两组直线所成的锐角(或直角)相等.异面直线所成的角(1)定义：a、b是两条异面直线，经过空间任意一点O，分别引直线a∥a,b∥b,则a 和b所成的锐角(或直角)叫做异面直线a和b所成的角.(2)取值范围：090.(3)求解方法①根据定义，通过平移，找到异面直线所成的角;②解含有的三角形，求出角的大小.5.直线和平面所成的角(1)定义和平面所成的角有三种：(i)垂线面所成的角的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角.(ii)垂线与平面所成的角直线垂直于平面，则它们所成的角是直角.(iii)一条直线和平面平行，或在平面内，则它们所成的角是0的角.(2)取值范围090(3)求解方法①作出斜线在平面上的射影，找到斜线与平面所成的角.②解含的三角形，求出其大小.③最小角定理斜线和平面所成的角，是这条斜线和平面内经过斜足的直线所成的一切角中最小的角，亦可说，斜线和平面所成的角不大于斜线与平面内任何直线所成的角.6.二面角及二面角的平面角(1)半平面直线把平面分成两个部分，每一部分都叫做半平面.(2)二面角条直线出发的两个半平面所组成的图形叫做二面角.这条直线叫做二面角的棱，这两个平面叫做二面角的面，即二面角由半平面一棱一半平面组成.若两个平面相交，则以两个平面的交线为棱形成四个二面角.二面角的大小用它的平面角来度量，通常认为二面角的平面角的取值范围是0180(3)二面角的平面角①以二面角棱上任意一点为端点，分别在两个面内作垂直于棱的射线，这两条射线所组成的角叫做二面角的平面角.如图，PCD是二面角-AB-的平面角.平面角PCD的大小与顶点C在棱AB上的位置无关.②二面角的平面角具有下列性质：(i)二面角的棱垂直于它的平面角所在的平面，即AB平面PCD.(ii)从二面角的平面角的一边上任意一点(异于角的顶点)作另一面的垂线，垂足必在平面角的另一边(或其反向延长线)上.(iii)二面角的平面角所在的平面与二面角的两个面都垂直，即平面PCD，平面PCD.③找(或作)二面角的平面角的主要方法.(i)定义法(ii)垂面法(iii)三垂线法(Ⅳ)根据特殊图形的性质(4)求二面角大小的常见方法①先找(或作)出二面角的平面角，再通过解三角形求得的值.②利用面积射影定理S=Scos其中S为二面角一个面内平面图形的面积，S是这个平面图形在另一个面上的射影图形的面积，为二面角的大小.③利用异面直线上两点间的距离公式求二面角的大小.7.空间的各种距离点到平面的距离(1)定义面外一点引一个平面的垂线，这个点和垂足间的距离叫做这个点到这个平面的距离.(2)求点面距离常用的方法：1)直接利用定义求①找到(或作出)表示距离的线段;②抓住线段(所求距离)所在三角形解之.2)利用两平面互相垂直的性质.即如果已知点在已知平面的垂面上，则已知点到两平面交线的距离就是所求的点面距离.3)体积法其步骤是：①在平面内选取适当三点，和已知点构成三棱锥;②求出此三棱锥的体积V和所取三点构成三角形的面积S;③由V=Sh，求出h即为所求.这种方法的优点是不必作出垂线即可求点面距离.难点在于如何构造合适的三棱锥以便于计算.4)转化法将点到平面的距离转化为(平行)直线与平面的距离来求.8.直线和平面的距离(1)定义一条直线和一个平面平行，这条直线上任意一点到平面的距离，叫做这条直线和平面的距离.(2)求线面距离常用的方法①直接利用定义求证(或连或作)某线段为距离，然后通过解三角形计算之.②将线面距离转化为点面距离，然后运用解三角形或体积法求解之.③作辅助垂直平面，把求线面距离转化为求点线距离.9.平行平面的距离(1)定义个平行平面同时垂直的直线，叫做这两个平行平面的公垂线.公垂线夹在两个平行平面间的部分，叫做这两个平行平面的公垂线段.两个平行平面的公垂线段的长度叫做这两个平行平面的距离.(2)求平行平面距离常用的方法①直接利用定义求证(或连或作)某线段为距离，然后通过解三角形计算之.②把面面平行距离转化为线面平行距离，再转化为线线平行距离，最后转化为点线(面)距离，通过解三角形或体积法求解之.10.异面直线的距离(1)定义条异面直线都垂直相交的直线叫做两条异面直线的公垂线.两条异面直线的公垂线在这两条异面直线间的线段的长度，叫做两条异面直线的距离.任何两条确定的异面直线都存在唯一的公垂线段.(2)求两条异面直线的距离常用的方法①定义法题目所给的条件，找出(或作出)两条异面直线的公垂线段，再根据有关定理、性质求出公垂线段的长.此法一般多用于两异面直线互相垂直的情形.②转化法为以下两种形式：线面距离面面距离③等体积法④最值法⑤射影法⑥公式法。