0021算法笔记——【贪心算法】贪心算法与活动安排问题
- 格式:docx
- 大小:101.17 KB
- 文档页数:8

贪⼼算法(会场安排问题、区间选点)学习算法课程之后的第⼀次记录,渐渐的,程序设计考虑的因素增多,程序=数据结构+算法,这个等式让我深有体会。
从开始简单的C++编程,再到选择合适数据结构,现在需要更进⼀步,从算法层次上考虑程序执⾏的效率。
我对算法的理解是⽤更少的开销获得更优的执⾏效果。
分治法、动态规划在此之前没有记录下来,学到贪⼼算法的时候,觉得需要总结⼀下学过的东西,也能更好的理解。
动态规划的设计,要满⾜最优⼦结构性质和重叠⼦问题,采⽤⾃底向上的策略,计算出最优值,找到整体最优解。
这个过程有时候挺难的,主要在写出递归式,要⾃底向上填表。
贪⼼策略有点像动态规划,但在⼀些⽅⾯是不同的,有时候贪⼼算法的思想更容易想到。
它要满⾜⼦问题最优⽽得到整体最优?两个条件:最优⼦结构性质和贪⼼选择性质。
满⾜贪⼼选择性质⼀定满⾜最优⼦结构性质,⽽满⾜最优⼦结构性质不⼀定满⾜贪⼼选择性质,⽐如背包问题可以⽤贪⼼算法解决,⽽0-1背包问题只能⽤动态规划。
典型的贪⼼问题活动安排,有n个活动,给出开始时间和结束时间,要尽可能安排多的活动(时间互相不冲突)。
解决这个问题正确的贪⼼思想是以每个活动结束时间为⽐较变量,按结束时间升序排好活动次序,接着就进⾏⽐较选择。
⽽会场安排问题与活动⼜有些不同之处,下⾯是我的解题过程。
7-2 会场安排问题 (20 分)假设要在⾜够多的会场⾥安排⼀批活动,并希望使⽤尽可能少的会场。
设计⼀个有效的贪⼼算法进⾏安排。
(这个问题实际上是著名的图着⾊问题。
若将每⼀个活动作为图的⼀个顶点,不相容活动间⽤边相连。
使相邻顶点着有不同颜⾊的最⼩着⾊数,相应于要找的最⼩会场数。
)输⼊格式:第⼀⾏有 1 个正整数k,表⽰有 k个待安排的活动。
接下来的 k⾏中,每⾏有 2个正整数,分别表⽰ k个待安排的活动开始时间和结束时间。
时间以 0 点开始的分钟计。
输出格式:输出最少会场数。
输⼊样例:51 2312 2825 3527 8036 50输出样例:3#include<iostream>#include<algorithm>using namespace std;struct node {int begin;int end;int flag;//标记该活动是否被安排,0表⽰未安排,1表⽰已安排}t[10001];int cmp(const node &a,const node &b)//⽐较规则:以结束时间升序排列{return a.end<b.end;}int main(){int i,j,n;node temp;cin>>n;for(i=0;i<n;i++){cin>>t[i].begin>>t[i].end;t[i].flag=0;}sort(t,t+n,cmp);int sum=0;//总共需要的会场数量for(i=0;i<n;i++)//⽅法2{if(!t[i].flag)//找到未安排的活动,进⾏场地安排{sum++;int p=i;for(j=p+1;j<n;j++)//当前活动结束时间与下⼀个活动开始不相交,则安排到同⼀个会场{if(t[p].end<=t[j].begin&&!t[j].flag){p=j;t[j].flag=1;}}t[i].flag=1;}}cout<<sum;return0;}View Code贪⼼策略为:把尽可能多的时间互不冲突的活动安排到⼀个会场,若活动时间交叉,则在安排到另⼀个会场。

0021算法笔记——【贪心算法】贪心算法与活动安排问题1、贪心算法(1)原理:在对问题求解时,总是做出在当前看来是最好的选择。
也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。
(2)特性:贪心算法采用自顶向下,以迭代的方法做出相继的贪心选择,每做一次贪心选择就将所求问题简化为一个规模更小的子问题,通过每一步贪心选择,可得到问题的一个最优解,虽然每一步上都要保证能获得局部最优解,但由此产生的全局解有时不一定是最优的,所以贪婪法不要回溯。
能够用贪心算法求解的问题一般具有两个重要特性:贪心选择性质和最优子结构性质。
1)贪心选择性质所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。
这是贪心算法可行的第一个基本要素。
贪心算法则通常以自顶向下的方式进行,以迭代的方式作出相继的贪心选择,每作一次贪心选择就将所求问题简化为规模更小的子问题。
对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所作的贪心选择最终导致问题的整体最优解。
证明的大致过程为:首先考察问题的一个整体最优解,并证明可修改这个最优解,使其以贪心选择开始。
做了贪心选择后,原问题简化为规模更小的类似子问题。
然后用数学归纳法证明通过每一步做贪心选择,最终可得到问题的整体最优解。
其中,证明贪心选择后的问题简化为规模更小的类似子问题的关键在于利用该问题的最优子结构性质。
2)最优子结构性质当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。
(3)贪心算法与动态规划算法的差异:动态规划和贪心算法都是一种递推算法,均有最优子结构性质,通过局部最优解来推导全局最优解。
两者之间的区别在于:贪心算法中作出的每步贪心决策都无法改变,因为贪心策略是由上一步的最优解推导下一步的最优解,而上一部之前的最优解则不作保留,贪心算法每一步的最优解一定包含上一步的最优解。




贪心算法的定义及应用贪心算法是一种高效的算法设计思路,无需寻找最优解算法或穷举所有可能解算法,而是通过每一步选择当前最好的策略,从而获得最终的最优解。
贪心算法是一种自顶向下的设计思路,它通过不断地逼近最优解路径,逐步确定每一步的决策方案,是目前计算机科学研究领域内广为应用的算法设计思路。
贪心算法的定义贪心算法顾名思义就是贪心,算法按照贪心的策略算出局部最优解,最终得到全局最优解。
其核心思想是,每次最优的选择一定会使最终结果最好。
贪心算法是指,在每一步,算法都会根据当前状态选择最好的决策方案。
然而应当注意的是,贪心算法的结果并不保证一定是最优的。
因此,在应用贪心算法时,需要评估算法的复杂度和效率,并确定贪心策略是否会导致漏算。
贪心算法应用贪心算法在生活中的应用广泛,例如网络中的最短路径、哈夫曼编码、任务调度等,以下是详细的应用介绍。
1. 集合覆盖问题假设你要向N个城市打广告,你需要选择一些卫星电视台,一台卫星电视台能够覆盖一定数量城市,并能发广告,如何选择卫星电视台来完成任务并覆盖所有城市?贪心算法解决此问题的步骤如下:(1)选出一个覆盖最多城市的卫星电视台。
(2)重复步骤1,直至所有城市都被完整覆盖。
2. 背包问题设有一个容量为W的背包和n个物品,第i个物品的价值为vi, 重量为wi,如何选择物品使得背包价值最大。
贪心算法解决此问题的步骤如下:(1)计算物品的性价比,即vi/wi。
(2)按照性价比从高到低排序。
(3)选取性价比最高的物品放入背包,直到背包已满。
(4)若背包未满,则选择性价比次高的物品放入背包。
3. 时间段最大利润问题给定一些项目,每个项目都有开始时间和结束时间,选择某些项目进行完成可以获得利润,如何选择获得最大利润?贪心算法解决此问题的步骤如下:(1)按照项目结束时间从早到晚排序。
(2)选择可以完成的项目中利润最大的。
(3)重复步骤2,直到所有项目都完成。
结语贪心算法作为一种高效的算法设计思路,在实际编程应用中可以帮助我们快速解决问题,提升程序效率。
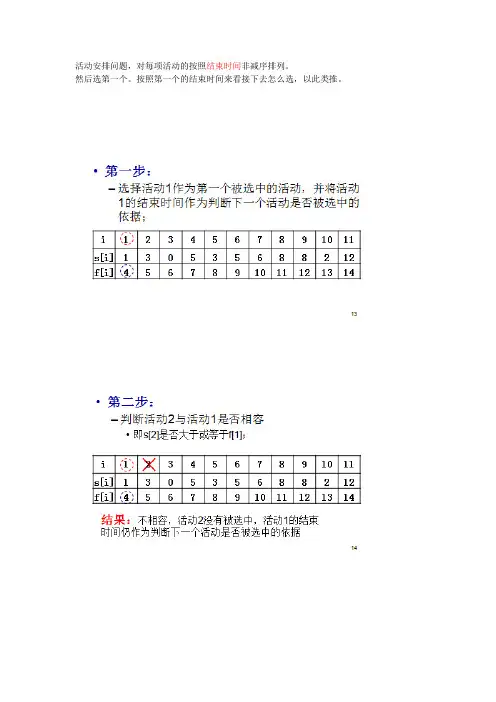
活动安排问题,对每项活动的按照结束时间非减序排列。
然后选第一个。
按照第一个的结束时间来看接下去怎么选,以此类推。
贪心选择性质的证明:
1.活动安排问题的一个最优解是以贪心选择开始。
即最优解包含第一个活动(叫做活动1)。
证明:假设有一个最优解叫做A。
它的活动也是以结束时间的非减序进行排列。
假设A中第一个活动叫做K。
如果K是我们的活动1,则A就是以活动1开始的。
如果K不是活动1.则把K从A中去掉,并加上活动1,而且活动1是相容的是因为活动1 的
结束时间最早。
所以证明了活动安排问题的一个最优解是以贪心选择开始。
最优子结构的证明:
把起始时间大于活动1的结束时间的活动去掉,A也可以把K去掉,这样子有一个递推的关系就是(总活动中)接下去那个与活动1相容的解必然可以相容在最优解(A-K)里面。
(因它又可以化为一个贪心选择的开始)所以每一步做出的贪心选择将使得原问题化为规模变小的相似的子问题。

算法设计贪心算法的思想与实现算法是计算机科学领域中的核心概念,它指导着解决问题的方法和步骤。
贪心算法是一种常用的算法设计思想,它在求解最优化问题时,每一步都采取当前状态下最优的选择,希望得到全局最优解。
本文将介绍贪心算法的思想和实现方式,并通过一个实际问题的案例来说明其应用。
一、贪心算法的思想贪心算法是一种贪心思想的应用,即每一步都做出在当前看来最好的选择。
它不关心整体的结果,只关心当下最优解。
贪心算法通常可以通过以下三个步骤实现:1. 贪心选择策略:在每一步中,通过一定的策略选择当前看来最优的解。
2. 确定限制条件:确定所得到的选择是否满足问题的限制条件。
3. 最优子结构:通过贪心选择策略,将原问题分解为若干子问题,每个子问题都具有最优子结构。
贪心算法的核心思想在于每一步都是局部最优解,通过一系列局部最优解,最终得到全局最优解。
然而,贪心算法并不能保证得到全局最优解,只适用于满足贪心选择策略、具有最优子结构和无后效性的问题。
二、贪心算法的实现贪心算法的实现通常分为以下几个步骤:1. 建立数学模型:通过数学表达式对问题进行建模。
2. 确定贪心选择策略:根据问题的特点和要求,确定一种贪心选择策略。
3. 构造贪心算法:根据贪心选择策略,构造出一个贪心算法来求解问题。
4. 证明算法的正确性:通过数学证明等方式,证明贪心算法得到的解是问题的最优解。
三、贪心算法的应用贪心算法可以应用于众多实际问题的求解,例如最小生成树、最短路径、背包问题等。
下面以活动选择问题为例来说明贪心算法的应用。
假设有n个活动,每个活动都有一个开始时间和结束时间。
要求从这些活动中选择出最多的互不冲突的活动(即活动之间不能出现时间上的重叠),请设计一个贪心算法来解决该问题。
算法步骤:1. 将活动按照结束时间的先后顺序进行排序。
2. 选择第一个活动作为已安排的活动。
3. 从剩余的活动中选择结束时间与已安排活动的开始时间不重叠的活动,将其加入到已安排的活动中。

贪心算法解析在计算机科学领域中,贪心算法是一种简单却高效的算法,主要用于解决优化问题。
贪心算法的基本思想是:每一步都选择当前最优的解决方案,最终得到全局最优解。
贪心算法的核心在于贪心策略。
贪心策略是指每一步都选取当前最优解,即对当前局部最优解不做考虑就直接进行决策。
贪心算法的优点在于其时间复杂度比较低,常常能够在很短的时间内找到一个不错的解决方案。
但是,使用贪心算法求解问题时需要注意,贪心算法要求问题具有最优子结构性质(即所有子问题的最优解能够推导出全局最优解),而且贪心算法并不能保证求得最优解。
下面通过几个实例来讲解贪心算法的应用。
例一:找零钱问题假设我们有 $n$ 种面额不同的硬币,它们的面值分别为 $v_1, v_2, ..., v_n$。
我们要找回 $p$ 元钱,问最少需要多少枚硬币。
这个问题可以用贪心算法来解决。
贪心策略是每次取尽量大的面额,直到找回的零钱等于 $p$ 元为止。
具体步骤如下:1. 将硬币按照面额从大到小排序;2. 依次取硬币,如果当前硬币的面额小于要找的零钱,就继续取;否则,取下一个硬币;3. 当找回的钱数等于 $p$ 时停止。
为了证明这个贪心算法确实是正确的,我们可以假设另外有一种更优的算法。
我们可以证明,如果这个算法与贪心算法在某一步不同时,那么这个算法肯定不是最优解。
因此,我们只需要证明贪心算法的每一步都能得到最优解,即可证明贪心算法是正确的。
例二:活动安排问题假设有一组活动,每个活动都有开始时间和结束时间。
假设活动 $i$ 的开始时间为 $s_i$,结束时间为 $f_i$。
问最多可以安排多少个活动。
这个问题可以用贪心算法来解决。
贪心策略是每次选择结束时间最早的活动。
具体步骤如下:1. 将活动按照结束时间从早到晚排序;2. 选择剩余结束时间最早的活动,将其加入集合中,将其结束时间赋值给变量 $last$;3. 对于接下来的活动,若其开始时间 $s_i \geq last$,则将其加入集合中,将其结束时间赋值给 $last$;否则,忽略这个活动。

计算机算法贪心算法基础知识全面解析计算机算法是计算机科学中的重要分支,它研究了如何有效地解决问题和执行任务。
在算法的研究中,贪心算法是一种常用且重要的策略。
本文将全面解析贪心算法的基础知识,包括其定义、特点、应用场景和实现方法。
一、贪心算法的定义和特点贪心算法是一种通过每一步的最优选择,最终达到整体的最优解的策略。
它的基本思想是总是做出在当前状态下看起来最好的选择,而不考虑其对未来的影响。
贪心算法具有以下特点:1. 简单:贪心算法通常思路简单,易于理解和实现。
2. 高效:贪心算法的时间复杂度通常较低,能够在较短的时间内得到近似最优解。
3. 局部最优:贪心算法每一步的选择都是局部最优的,但不一定能够得到全局最优解。
二、贪心算法的应用场景贪心算法在解决一些最优化问题、组合优化问题和调度问题等方面有广泛的应用。
下面列举几个常见的应用场景。
1. 钱币找零:给定不同面额的硬币和一个要找零的金额,贪心算法可以求解找零所需的最小硬币数。
2. 区间覆盖:给定一组区间,选择尽可能少的区间,使得它们的并集覆盖给定的区间。
3. 任务调度:给定一组任务和它们所需的执行时间,贪心算法可以求解在最短时间内完成所有任务的调度顺序。
4. 哈夫曼编码:根据字符出现的频率构建最优的前缀编码树,用于数据压缩和传输。
三、贪心算法的实现方法贪心算法的实现通常分为以下两种方法:1. 按优先级选择:根据问题的具体要求,将可选的方案按照优先级进行排序,每次选择优先级最高的方案。
2. 按增量选择:从问题的初始状态开始,通过每一步的选择逐步构建解决方案,直到达到最终状态。
不同的问题会适用不同的实现方法,需要根据具体情况选择最合适的策略。
总结:贪心算法是一种常用且重要的算法策略,通过每一步的最优选择达到整体最优解。
它的简单性和高效性使得它在实际问题中有广泛的应用。
我们通过定义和特点、应用场景以及实现方法等方面,对贪心算法的基础知识进行了全面解析。
对于进一步学习和探索贪心算法,可以深入研究不同应用领域下的具体案例和算法实现。

贪婪算法(贪⼼算法)贪⼼算法简介:@anthor:QYX 贪⼼算法是指:在每⼀步求解的步骤中,它要求“贪婪”的选择最佳操作,并希望通过⼀系列的最优选择,能够产⽣⼀个问题的(全局的)最优解。
贪⼼算法每⼀步必须满⾜⼀下条件: 1、可⾏的:即它必须满⾜问题的约束。
2、局部最优:他是当前步骤中所有可⾏选择中最佳的局部选择。
3、不可取消:即选择⼀旦做出,在算法的后⾯步骤就不可改变了。
贪⼼算法的定义:贪⼼算法是指在对问题求解时,总是做出在当前看来是最好的选择。
也就是说,不从整体最优上加以考虑,只做出在某种意义上的局部最优解。
贪⼼算法不是对所有问题都能得到整体最优解,关键是贪⼼策略的选择,选择的贪⼼策略必须具备⽆后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
解题的⼀般步骤是:1.建⽴数学模型来描述问题;2.把求解的问题分成若⼲个⼦问题;3.对每⼀⼦问题求解,得到⼦问题的局部最优解;4.把⼦问题的局部最优解合成原来问题的⼀个解。
如果⼤家⽐较了解动态规划,就会发现它们之间的相似之处。
最优解问题⼤部分都可以拆分成⼀个个的⼦问题,把解空间的遍历视作对⼦问题树的遍历,则以某种形式对树整个的遍历⼀遍就可以求出最优解,⼤部分情况下这是不可⾏的。
贪⼼算法和动态规划本质上是对⼦问题树的⼀种修剪,两种算法要求问题都具有的⼀个性质就是⼦问题最优性(组成最优解的每⼀个⼦问题的解,对于这个⼦问题本⾝肯定也是最优的)。
动态规划⽅法代表了这⼀类问题的⼀般解法,我们⾃底向上构造⼦问题的解,对每⼀个⼦树的根,求出下⾯每⼀个叶⼦的值,并且以其中的最优值作为⾃⾝的值,其它的值舍弃。
⽽贪⼼算法是动态规划⽅法的⼀个特例,可以证明每⼀个⼦树的根的值不取决于下⾯叶⼦的值,⽽只取决于当前问题的状况。
换句话说,不需要知道⼀个节点所有⼦树的情况,就可以求出这个节点的值。
由于贪⼼算法的这个特性,它对解空间树的遍历不需要⾃底向上,⽽只需要⾃根开始,选择最优的路,⼀直⾛到底就可以了。
贪心算法总结什么是贪心算法?贪心算法(Greedy Algorithm)是一种用于求解优化问题的常见算法,其核心思想是在每一步都选择当前最优解,希望最终能够得到全局最优解。
贪心算法在每一步仅考虑局部最优,而不关心全局最优,因此它的计算速度较快。
然而,由于贪心算法没有考虑全局,在某些情况下可能无法得到最优解。
贪心算法并不适用于所有的问题,只适用于一些特殊的问题,例如背包问题、最小生成树问题等。
在实际应用中,需要根据具体问题的特点来判断是否可以使用贪心算法来解决。
贪心算法的基本思路贪心算法的基本思路可以概括为以下几步:1.确定最优解的性质:首先要确定在每一步选择中,能够得到局部最优解。
2.构造贪心选择:根据最优解的性质,每一步都做出一个贪心选择,选择能够获得当前最大或最小收益的方案。
3.确定限制条件:确定问题的限制条件,包括物品的容量、时间限制等。
4.根据限制条件,进行剪枝策略:如果某种选择在限制条件下无法满足要求,则需要进行剪枝,排除该选择。
5.循环执行贪心选择,直到问题得到解决。
贪心算法的优缺点贪心算法具有以下优点:•计算速度快:贪心算法在每一步只考虑局部最优解,不需要对全局进行搜索,因此计算速度较快。
•算法思路简单:贪心算法的思路相对简单,易于理解和实现。
•适用范围广:贪心算法适用于一些特殊问题,如最短路径、最小生成树等。
然而,贪心算法也存在一些缺点:•可能无法得到最优解:由于贪心算法仅考虑局部最优解,而不关心全局最优解,因此可能无法得到最优解。
•需要满足贪心选择性质:贪心算法要求问题具有贪心选择性质,即每一步都能够得到局部最优解。
如果问题不具备这个性质,贪心算法可能不适用。
贪心算法的应用场景贪心算法适用于一些特殊的问题,以下是一些常见的应用场景:1. 最短路径问题最短路径问题是指在一个加权有向图中,找出从一个顶点到另一个顶点的最短路径。
贪心算法可以用来解决一些简单的最短路径问题,如Dijkstra算法。
贪心算法解决活动安排问题金潇Use the greedy algorithm to solve the arrangement for activitiesJinxiao摘要:贪心算法在当前来看是最好的选择。
是用利用启发式策略,在不从整体最优上加以考虑的情况下,来做出局部最优选择的一种算法。
本文通过贪心算法的经典案例—活动安排问题入手,描述了贪心算法的基本思想和可能产生的问题,并简述该算法的好处和特点,最后给出几种经典的贪心算法。
关键字:贪心算法、局部最优选择Abstract:A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stage with the hope of finding the global optimum. This article through the greedy algorithm of the classic case--activities problems, describes the greedy algorithm the basic ideas and possible problems, and briefly introduces the advantages and characteristics of the algorithm, and finally gives several classic the greedy algorithm. Keywords:greedy algorithm、the locally optimal choice1.引言:贪心法是一种改进了的分级处理方法。
用贪心法设计算法的特点是一步一步地进行,每一步上都要保证能获得局部最优解。
贪心算法理解贪心算法的基本原理和应用场景贪心算法:理解贪心算法的基本原理和应用场景简介:贪心算法(Greedy Algorithm)是一种常用的算法设计和解决问题的方法。
它以一种贪婪的方式做出每一步的选择,希望最终能够达到整体上的最优解。
本文将介绍贪心算法的基本原理和常见应用场景。
一、贪心算法的基本原理贪心算法的基本原理是每次都做出当前最优的选择,希望最终能够达到整体上的最优解。
贪心算法的优点在于简单、高效,但由于它只关注当前最优解,因此可能无法得到全局最优解。
贪心算法的基本步骤如下:1. 将问题划分为若干子问题,每个子问题都有多个选择;2. 分析子问题的选择,以及每个选择的最优解;3. 根据每个子问题的最优解,做出当前最优的选择;4. 更新已做出选择的子问题集合;5. 重复步骤3和4,直到解决全部子问题。
二、贪心算法的应用场景1. 零钱兑换问题零钱兑换问题是指给定一个金额和一组零钱的面值,如何用最少数量的零钱找零。
贪心算法可以从面值最大的零钱开始,每次找零选择当前面值最大的零钱,直到达到目标金额。
2. 区间调度问题区间调度问题是指给定一组区间,如何选择最多数量的不相交区间。
贪心算法可以根据区间的结束时间进行排序,每次选择结束时间最早的区间,并排除与之重叠的其他区间。
3. 背包问题背包问题是指给定一组物品和一个固定容量的背包,如何选择物品放入背包,使得背包中物品的总价值最大。
贪心算法可以通过计算每个物品的单位价值(即物品的价值与重量的比值)来选择单位价值最高的物品放入背包。
4. 最短路径问题最短路径问题是指在一个有向图或无向图中,找到两个节点之间的最短路径。
贪心算法可以使用Dijkstra算法,每次选择离起始节点最近的未访问节点进行扩展,直到找到目标节点。
5. 活动选择问题活动选择问题是指在一组活动中,选出最大的互相兼容的活动子集合。
贪心算法可以根据活动的结束时间进行排序,每次选择结束时间最早的活动,并排除与之重叠的其他活动。
《算法导论》读书笔记之第16章贪心算法—活动选择问题前言:贪心算法也是用来解决最优化问题,将一个问题分成子问题,在现在子问题最优解的时,选择当前看起来是最优的解,期望通过所做的局部最优选择来产生一个全局最优解。
书中先从活动选择问题来引入贪心算法,分别采用动态规划方法和贪心算法进行分析。
本篇笔记给出活动选择问题的详细分析过程,并给出详细的实现代码进行测试验证。
关于贪心算法的详细分析过程,下次在讨论。
1、活动选择问题描述有一个需要使用每个资源的n个活动组成的集合S= {a1,a2,···,a n },资源每次只能由一个活动使用。
每个活动a i都有一个开始时间s i 和结束时间f i,且0≤s i<f i<∞。
一旦被选择后,活动a i就占据半开时间区间[s i,f i)。
如果[s i,f i]和[s j,f j]互不重叠,则称a i和a j两个活动是兼容的。
该问题就是要找出一个由互相兼容的活动组成的最大子集。
例如下图所示的活动集合S,其中各项活动按照结束时间单调递增排序。
从图中可以看出S中共有11个活动,最大的相互兼容的活动子集为:{a1,a4,a8,a11,}和{a2,a4,a9,a11}。
2、动态规划解决过程(1)活动选择问题的最优子结构定义子问题解空间S ij是S的子集,其中的每个获得都是互相兼容的。
即每个活动都是在a i结束之后开始,且在a j开始之前结束。
为了方便讨论和后面的计算,添加两个虚构活动a0和a n+1,其中f0=0,s n+1=∞。
结论:当i≥j时,S ij为空集。
如果活动按照结束时间单调递增排序,子问题空间被用来从S ij中选择最大兼容活动子集,其中0≤i<j≤n+1,所以其他的S ij都是空集。
最优子结构为:假设S ij的最优解A ij包含活动a k,则对S ik的解A ik和S kj的解A kj必定是最优的。
通过一个活动a k将问题分成两个子问题,下面的公式可以计算出S ij的解A ij。
算法导论——贪心算法求解最优化问题的算法通常需要经过一系列的步骤,在每个步骤都面临多种选择。
对于许多最优化问题,使用动态规划算法来求最优解有些杀鸡用牛刀了,可以使用更简单、更高效的算法。
贪心算法(greedy algorithm)就是这样的算法,它在每一步都做出当时看起来最佳的选择。
也就是说,它总是做出局部最优的选择,寄希望这样的选择能导致全局最优解。
本章介绍一些贪心算法能找到最优解的最优化问题。
贪心算法并不保证得到最优解,但对很多问题确实可以求得最优解。
我们首先在16.1节介绍一个简单但非平凡的问题—活动选择问题,这是一个可以用贪心算法求得最优解的问题。
首先考虑用动态规划方法解决这个问题,然后证明一直做出贪心选择就可以得到最优解,从而得到一个贪心算法。
16. 2节会回顾贪心方法的基本要素,并给出一个直接的方法,可用来证明贪心算法的正确性。
16. 3节提出贪心技术的一个重要应用:设计数据压缩编码(Huffman编码)。
在16. 4节中,我们讨论一种称为“拟阵"(matroid)的组合结构的理论基础,贪心算法总是能获得这种结构的最优解。
最后,16. 5节将拟阵应用于单位时间任务调度问题,每个任务均有截止时间和超时惩罚。
贪心方法是一种强有力的算法设计方法,可以很好地解决很多问题。
在后面的章节中,我们会提出很多利用贪心策略设计的算法,包括最小生成树(minimum-spanning-tree)算法(第23章)、单源最短路径的djikstra算法(第24章),以及集合覆盖问题的Chvatal贪心启发式算法(第35章)。
最小生成树算法提供了一个经典的贪心方法的例子。
16.1 贪心选择假如我们无需求解所有子问题就可以选择出一个活动加人到最优解,将会怎样?这将使我们省去递归式(16. 2)中固有的考查所有选择的过程。
实际上,对于活动选择问题,我们只需考虑一个选择:贪心选择。
对于活动选择问题,什么是贪心选择?直观上,我们应该选择这样一个活动,选出它后剩下的资源应能被尽量多的其他任务所用。
运用贪心算法解决活动安排问题李文治,陈平,谢华欣,韩月梅(陕西师范大学计算机科学学院09级软件工程,西安,710062)摘要:生活中经常可以遇到这样一些问题,需要对一些资源进行优化分配已达到资源利用率的最大化。
如对会场会议的安排、对赛场比赛的安排、课程的安排、以及扩展到电脑中操作系统对不同进程资源的分配问题。
使用贪心算法可以很快的解决此类安排问题。
关键词:活动安排安排;贪心算法;Using the greedy algorithm to solve the problem of activityarrangementLi Wenzhi, Chen Ping, Xie Huaxin, Han Y uemei( Shaanxi Normal University computer science institute of software engineering, Xi'an, 710062)Abstract:life can often encounter such problems, the need for some resource optimized allocation has achieve the maximization of resource utilization. As for the meeting venue arrangement, the Games arrangement, the arrangement of the courses, as well as an extension to the computer operating system on the process of different resource allocation problems. The use of greedy algorithm can quickly solve such arrangements.Keywords:activity arrangement; greedy algorithm;1引言生活中经常可以遇到这样一些问题,需要对一些资源进行优化分配已达到资源利用率的最大化。
0021算法笔记——【贪心算法】贪心算法与活动安排问题1、贪心算法(1)原理:在对问题求解时,总是做出在当前看来是最好的选择。
也就是说,不从整体最优上加以考虑,他所做出的仅是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,但对范围相当广泛的许多问题他能产生整体最优解或者是整体最优解的近似解。
(2)特性:贪心算法采用自顶向下,以迭代的方法做出相继的贪心选择,每做一次贪心选择就将所求问题简化为一个规模更小的子问题,通过每一步贪心选择,可得到问题的一个最优解,虽然每一步上都要保证能获得局部最优解,但由此产生的全局解有时不一定是最优的,所以贪婪法不要回溯。
能够用贪心算法求解的问题一般具有两个重要特性:贪心选择性质和最优子结构性质。
1)贪心选择性质所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。
这是贪心算法可行的第一个基本要素。
贪心算法则通常以自顶向下的方式进行,以迭代的方式作出相继的贪心选择,每作一次贪心选择就将所求问题简化为规模更小的子问题。
对于一个具体问题,要确定它是否具有贪心选择性质,必须证明每一步所作的贪心选择最终导致问题的整体最优解。
证明的大致过程为:首先考察问题的一个整体最优解,并证明可修改这个最优解,使其以贪心选择开始。
做了贪心选择后,原问题简化为规模更小的类似子问题。
然后用数学归纳法证明通过每一步做贪心选择,最终可得到问题的整体最优解。
其中,证明贪心选择后的问题简化为规模更小的类似子问题的关键在于利用该问题的最优子结构性质。
2)最优子结构性质当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。
(3)贪心算法与动态规划算法的差异:动态规划和贪心算法都是一种递推算法,均有最优子结构性质,通过局部最优解来推导全局最优解。
两者之间的区别在于:贪心算法中作出的每步贪心决策都无法改变,因为贪心策略是由上一步的最优解推导下一步的最优解,而上一部之前的最优解则不作保留,贪心算法每一步的最优解一定包含上一步的最优解。
动态规划算法中全局最优解中一定包含某个局部最优解,但不一定包含前一个局部最优解,因此需要记录之前的所有最优解。
(4)基本思路:1)建立数学模型来描述问题。
2)把求解的问题分成若干个子问题。
3)对每一子问题求解,得到子问题的局部最优解。
4)把子问题的解局部最优解合成原来解问题的一个解。
2、活动安排问题活动安排问题就是要在所给的活动集合中选出最大的相容活动子集合,是可以用贪心算法有效求解的很好例子。
该问题要求高效地安排一系列争用某一公共资源的活动。
贪心算法提供了一个简单、漂亮的方法使得尽可能多的活动能兼容地使用公共资源。
问题描述:设有n个活动的集合E={1,2,…,n},其中每个活动都要求使用同一资源,如演讲会场等,而在同一时间内只有一个活动能使用这一资源。
每个活动i都有一个要求使用该资源的起始时间si和一个结束时间fi,且si<fi。
如果选择了活动i,则它在半开时间区间[si, fi)内占用资源。
若区间[si, fi)与区间[sj, fj)不相交,则称活动i与活动j是相容的。
也就是说,当si≥fj或sj≥fi时,活动i与活动j相容。
活动安排问题就是要在所给的活动集合中选出最大的相容活动子集合。
求解思路:将活动按照结束时间进行从小到大排序。
然后用i代表第i个活动,s[i]代表第i个活动开始时间,f[i]代表第i个活动的结束时间。
按照从小到大排序,挑选出结束时间尽量早的活动,并且满足后一个活动的起始时间晚于前一个活动的结束时间,全部找出这些活动就是最大的相容活动子集合。
事实上系统一次检查活动i是否与当前已选择的所有活动相容。
若相容活动i加入已选择活动的集合中,否则,不选择活动i,而继续下一活动与集合A中活动的相容性。
若活动i与之相容,则i成为最近加入集合A的活动,并取代活动j的位置。
下面给出求解活动安排问题的贪心算法,各活动的起始时间和结束时间存储于数组s和f中,且按结束时间的非减序排列。
如果所给的活动未按此序排列,可以用O(nlogn)的时间重排。
具体代码如下:[cpp]view plain copy1.//4d1 活动安排问题贪心算法2.#include "stdafx.h"3.#include <iostream>ing namespace std;5.6.template<class Type>7.void GreedySelector(int n, Type s[], Type f[], bool A[]);8.9.const int N = 11;10.11.int main()12.{13.//下标从1开始,存储活动开始时间14.int s[] = {0,1,3,0,5,3,5,6,8,8,2,12};15.16.//下标从1开始,存储活动结束时间17.int f[] = {0,4,5,6,7,8,9,10,11,12,13,14};18.19.bool A[N+1];20.21. cout<<"各活动的开始时间,结束时间分别为:"<<endl;22.for(int i=1;i<=N;i++)23. {24. cout<<"["<<i<<"]:"<<"("<<s[i]<<","<<f[i]<<")"<<endl;25. }26. GreedySelector(N,s,f,A);27. cout<<"最大相容活动子集为:"<<endl;28.for(int i=1;i<=N;i++)29. {30.if(A[i]){31. cout<<"["<<i<<"]:"<<"("<<s[i]<<","<<f[i]<<")"<<endl;32. }33. }34.35.return 0;36.}37.38.template<class Type>39.void GreedySelector(int n, Type s[], Type f[], bool A[])40.{41. A[1]=true;42.int j=1;//记录最近一次加入A中的活动43.44.for (int i=2;i<=n;i++)//依次检查活动i是否与当前已选择的活动相容45. {46.if (s[i]>=f[j])47. {48. A[i]=true;49. j=i;50. }51.else52. {53. A[i]=false;54. }55. }56.}由于输入的活动以其完成时间的非减序排列,所以算法greedySelector每次总是选择具有最早完成时间的相容活动加入集合A中。
直观上,按这种方法选择相容活动为未安排活动留下尽可能多的时间。
也就是说,该算法的贪心选择的意义是使剩余的可安排时间段极大化,以便安排尽可能多的相容活动。
算法greedySelector的效率极高。
当输入的活动已按结束时间的非减序排列,算法只需O(n)的时间安排n个活动,使最多的活动能相容地使用公共资源。
如果所给出的活动未按非减序排列,可以用O(nlogn)的时间重排。
例:设待安排的11个活动的开始时间和结束时间按结束时间的非减序排列如下:算法greedySelector的计算过程如下图所示。
图中每行相应于算法的一次迭代。
阴影长条表示的活动是已选入集合A的活动,而空白长条表示的活动是当前正在检查相容性的活动。
若被检查的活动i的开始时间Si小于最近选择的活动j的结束时间fi,则不选择活动i,否则选择活动i加入集合A中。
贪心算法并不总能求得问题的整体最优解。
但对于活动安排问题,贪心算法greedySelector却总能求得的整体最优解,即它最终所确定的相容活动集合A的规模最大。
这个结论可以用数学归纳法证明。
证明如下:设E={0,1,2,…,n-1}为所给的活动集合。
由于E 中活动安排安结束时间的非减序排列,所以活动0具有最早完成时间。
首先证明活动安排问题有一个最优解以贪心选择开始,即该最优解中包含活动0.设a是所给的活动安排问题的一个最优解,且a中活动也按结束时间非减序排列,a中的第一个活动是活动k。
如k=0,则a就是一个以贪心选择开始的最优解。
若k>0,则我们设b=a-{k}∪{0}。
由于end[0] ≤end[k],且a中活动是互为相容的,故b中的活动也是互为相容的。
又由于b中的活动个数与a中活动个数相同,且a是最优的,故b也是最优的。
也就是说b是一个以贪心选择活动0开始的最优活动安排。
因此,证明了总存在一个以贪心选择开始的最优活动安排方案,也就是算法具有贪心选择性质。
程序运行结果如下:。