第二章 数理逻辑

高一数学现代数学阅读附答案可以的，下面是你所要求的文档：在这份文档中，我们将提供高一数学现代数学的阅读材料，并附上答案供参考。

以下是各个章节的内容介绍和相关的练题和答案。

第一章：集合论本章将介绍集合论的基本概念和运算方法。

通过研究本章，学生将深入了解集合的逻辑关系和基本运算。

以下是练题和答案：1. 什么是集合的并集运算？试举例说明。

答案：集合A和集合B的并集，表示为A∪B，是包含了A和B中所有元素的集合。

例如，A = {1, 2, 3}，B = {3, 4, 5}，则A∪B = {1, 2, 3, 4, 5}。

2. 什么是集合的交集运算？给出一个具体的例子。

答案：集合A和集合B的交集，表示为A∩B，是包含了同时属于A和B的元素的集合。

例如，A = {1, 2, 3}，B = {3, 4, 5}，则A∩B = {3}。

第二章：数理逻辑本章将介绍数理逻辑的基本原理和运算规则。

通过研究本章，学生将掌握数理逻辑中的命题、联结词和推理规则。

以下是练题和答案：1. 什么是命题逻辑中的合取运算？举一个具体的例子。

答案：命题逻辑中的合取运算，也称为逻辑与运算，表示为∧。

它要求两个命题同时为真时结果为真，其他情况均为假。

例如，对于命题P：“今天是星期一”和命题Q：“天气晴朗”，当P和Q同时成立时，P∧Q为真。

2. 什么是命题逻辑中的析取运算？给出一个具体的例子。

答案：命题逻辑中的析取运算，也称为逻辑或运算，表示为∨。

它要求两个命题至少有一个为真时结果为真，其他情况均为假。

例如，对于命题P：“今天是星期一”和命题Q：“天气晴朗”，当P和Q中只要有一个成立时，P∨Q为真。

第三章：概率论本章将介绍概率论的基本概念和计算方法。

通过研究本章，学生将能够理解概率的定义、计算概率的方法和概率与事件的关系。

以下是练题和答案：1. 什么是事件的概率？如何计算事件的概率？答案：事件的概率是指该事件发生的可能性。

计算事件的概率可以通过计算有利结果的数量与总可能结果的数量之比来得到。

初二数学数理逻辑的基本概念与应用数理逻辑是数学的一个重要分支，它研究的是关于命题、推理和证明的基本规律。

初中数学教育中，数理逻辑的学习有助于培养学生的逻辑思维能力，提高解决问题的能力。

本文将介绍初二数学数理逻辑的基本概念与应用。

一、命题与命题的逻辑连接词命题是陈述性句子，其内容可以被判定为真或假。

在数理逻辑中常用字母P、Q、R等表示命题。

命题的逻辑连接词有与、或、非、蕴含、等价等。

其中，与表示同时满足两个命题，或表示满足其中之一或两者均满足，非表示取反，蕴含表示若命题A成立，则命题B也必定成立，等价表示两个命题具有相同的真值。

二、真值表与命题的逻辑运算真值表是用来表示不同情况下命题的真假取值的表格。

对于n个命题，其真值表一共有2^n行。

通过真值表可以清晰地展示命题之间的逻辑运算关系。

在数理逻辑中，通过运用真值表可以判断命题之间的逻辑等价性，从而简化问题的求解。

三、充分条件与必要条件充分条件与必要条件是描述命题之间关系的重要概念。

如果命题A成立是命题B成立的条件，那么称A是B的充分条件，B是A的必要条件。

例如，命题A：某人是男性；命题B：某人能上军校。

那么，A是B的充分条件，B是A的必要条件。

数理逻辑中，通过充分条件与必要条件可以进行逆否、逆否命题的推理。

四、命题的推理与证明命题的推理是数理逻辑中的核心内容，它通过合理的推理关系来得出新的命题。

常见的推理方法包括：直接推理、间接推理、归谬法等。

证明是数学中重要的思维方式，通过逻辑推理和严密的论证来验证数学命题的正确性。

初二数学中常见的证明方法有直接证明、间接证明、反证法等。

五、数理逻辑在数学问题中的应用数理逻辑在数学问题中有广泛的应用，通过运用数理逻辑，能够解决一些复杂的问题。

数理逻辑的应用包括：1. 排列组合问题：通过运用命题的逻辑运算，可以得出不同条件下的排列组合问题的解答方法，如“有6本不同的书放入两个箱子中，计算放法的总数”。

2. 方程与不等式的解：通过分析命题的充分条件和必要条件，可以得出方程与不等式的解集，如“解方程2x-5=9”。

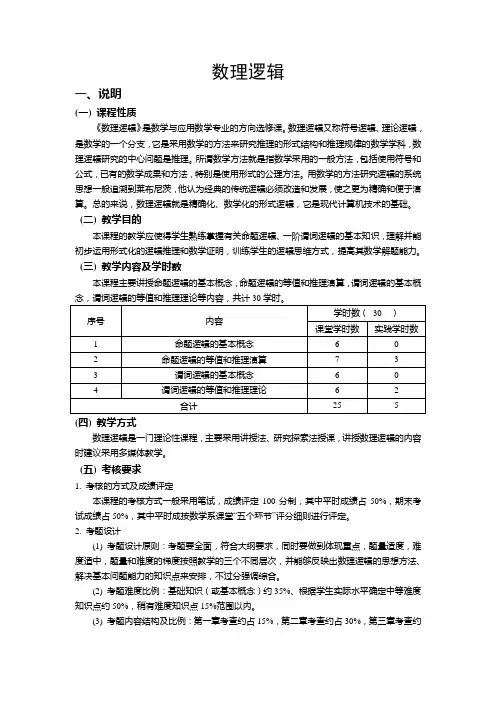
数理逻辑一、说明(一) 课程性质《数理逻辑》是数学与应用数学专业的方向选修课。

数理逻辑又称符号逻辑、理论逻辑，是数学的一个分支，它是采用数学的方法来研究推理的形式结构和推理规律的数学学科，数理逻辑研究的中心问题是推理。

所谓数学方法就是指数学采用的一般方法，包括使用符号和公式，已有的数学成果和方法，特别是使用形式的公理方法。

用数学的方法研究逻辑的系统思想一般追溯到莱布尼茨，他认为经典的传统逻辑必须改造和发展，使之更为精确和便于演算。

总的来说，数理逻辑就是精确化、数学化的形式逻辑，它是现代计算机技术的基础。

(二) 教学目的本课程的教学应使得学生熟练掌握有关命题逻辑、一阶谓词逻辑的基本知识，理解并能初步运用形式化的逻辑推理和数学证明，训练学生的逻辑思维方式，提高其数学解题能力。

(三) 教学内容及学时数本课程主要讲授命题逻辑的基本概念，命题逻辑的等值和推理演算，谓词逻辑的基本概念，谓词逻辑的等值和推理理论等内容，共计30学时。

序号内容学时数（30 ）课堂学时数实践学时数1 命题逻辑的基本概念 6 02 命题逻辑的等值和推理演算7 33 谓词逻辑的基本概念 6 04 谓词逻辑的等值和推理理论 6 2合计25 5 (四) 教学方式数理逻辑是一门理论性课程，主要采用讲授法、研究探索法授课，讲授数理逻辑的内容时建议采用多媒体教学。

(五) 考核要求1. 考核的方式及成绩评定本课程的考核方式一般采用笔试，成绩评定100分制，其中平时成绩占50%，期末考试成绩占50%，其中平时成按数学系课堂“五个环节”评分细则进行评定。

2. 考题设计(1) 考题设计原则：考题要全面，符合大纲要求，同时要做到体现重点，题量适度，难度适中，题量和难度的梯度按照教学的三个不同层次，并能够反映出数理逻辑的思想方法、解决基本问题能力的知识点来安排，不过分强调综合。

(2) 考题难度比例：基础知识（或基本概念）约35%、根据学生实际水平确定中等难度知识点约50%，稍有难度知识点15%范围以内。

离散数学之数理逻辑2第一篇数理逻辑数理逻辑是应用数学方法引进一套符号系统来研究思维的形式结构和规律的学科，它起源于公元十七世纪。

十九世纪英国的德·摩根和乔治·布尔发展了逻辑代数，二十世纪三十年代数理逻辑进入了成熟时期，基本内容（命题逻辑和谓词逻辑）有了明确的理论基础，成为数学的一个重要分支，同时也是电子元件设计和性质分析的工具。

冯·诺意曼，图灵，克林，…等人研究了逻辑与计算的关系。

基于理论研究和实践，随着1946年第一台通用电子数字计算机的诞生和近代科学的发展，计算技术中提出了大量的逻辑问题，逻辑程序设计语言的研制，更促进了数理逻辑的发展。

除古典二值（真，假）逻辑外，还研究了多值逻辑、模态逻辑、概率逻辑、模糊逻辑、非单调逻辑等。

不仅有演绎逻辑，也还有归纳逻辑。

计算机科学中还专门研究计算逻辑、程序逻辑、时序逻辑等。

现代数理逻辑分为四论：证明论，递归论（它们与形式语言语法有关），模型论，公理化集合论（它们与形式语言的语义有关）。

第1-1章命题逻辑学习要求: 掌握命题，命题公式，重言式，等价式，蕴涵式等基本概念，能利用逻辑联结词或真值表，等价式与蕴涵式进行命题演算和推理；学习范式时与集合的范式进行对比。

表述客观世界的各种现象，表述人们的思想，表述各门学科的规则、理论等，除使用自然语言（这常常是上有歧异性的）外，还要使用一些特定的术语、符号、规律等“对象语言”，这些是所研究学科的一种特殊的形式化语言，研究思维结构与规律的逻辑学也有其对象语言。

本章就是讨论逻辑学中的对象语言—命题及其演算，它相当于自然语言中的语句。

§1-1-1 命题逻辑联结词与真值表一、命题的基本概念首先我们从下面的例子加以分析。

例1-1-1.1人总是要死的。

例1-1-1.2苏格拉底是人。

例1-1-1.3苏格拉底是要死的。

例1-1-1.4中国人民是勤劳和勇敢的。

例1-1-1.5鸵鸟是鸟。

例1-1-1.6 1是质（素）数。

大学数学数理逻辑数理逻辑是大学数学中的一门重要学科，它研究命题、论证和推理的规律和方法。

数理逻辑在数学、计算机科学、哲学等领域有着广泛的应用。

本文将从数理逻辑的基本概念、命题逻辑和谓词逻辑等方面进行论述，以帮助读者更好地理解和应用数理逻辑。

一、数理逻辑的概念和基本原理数理逻辑，又称形式逻辑，是一种通过形式化的符号系统来研究命题、论证和推理的学科。

它主要关注推理的正确性和有效性，旨在分析命题之间的逻辑关系，并通过推理规则来推断新的结论。

数理逻辑的基本原理包括命题、谓词、量词和推理规则等。

命题是陈述句，可以为真或者假，其真值可以通过逻辑运算进行组合。

谓词是对对象进行描述的函数，通过给定一个或多个对象来判断一个命题的真值。

量词用来量化命题中的变量，包括全称量词和存在量词。

推理规则是根据数理逻辑的规则进行合乎逻辑的推理步骤，如假言推理、略化推理等。

二、命题逻辑命题逻辑是数理逻辑的一个重要分支，它研究命题之间的逻辑关系。

命题逻辑主要包括命题的联结词、真值表和等价演算等。

1. 命题的联结词命题的联结词包括合取（∧）、析取（∨）、蕴含（→）和否定（¬）等，分别表示与、或、蕴含和非的关系。

通过这些联结词，可以对多个命题进行逻辑运算，得到一个新的命题。

2. 真值表真值表是用来列出所有可能的取值情况，并给出联结词的运算结果。

通过真值表，可以判断联结词的真值和命题之间的逻辑关系。

3. 等价演算等价演算是通过代换规则和等价关系，将逻辑表达式转化为等价的形式。

常用的等价演算规则包括分配律、德摩根律等，它们使得逻辑表达式的推导更加简化和便捷。

三、谓词逻辑谓词逻辑是数理逻辑的另一个重要分支，它引入了谓词和量词的概念，用于更精确地描述和推理命题。

谓词逻辑主要包括谓词符号、量词和量词的运用等。

1. 谓词符号谓词符号是用来描述对象的属性或者关系的符号，它通常代表一个函数，通过给定一个或多个参数来判断命题的真值。

谓词符号包括等于（=）、大于（>）等，通过它们可以对对象进行进一步的描述和区分。

马琦 2010.9.4 maqi08@学习逻辑的目的之一：对推理过程的分析。

前一章：将语句 语句和论证 语句 论证抽象到形式，并且对 论证 一个有效的论证 有效的论证给出了直觉的定义。

有效的论证 本章：引进形式演绎系统 形式演绎系统的概念，本质上是 形式演绎系统 抽象过程的继续，从中概括出证明 证明的概念。

证明形式系统符号字母表 合式公式：符号有穷串的集合 合式公式 公理：某些合式公式的集合 公理 演绎规则：可推出一个合式公式作为 演绎规则 合式公式有穷集的直接后承。

根据以上四点，就可以从公理出发， 使用推理规则依次完成演绎的过程。

系统元素（ 元素（项） 运算符号字母表： 符号字母表 ~,→,( , ) , p1, p2, p3,… 合式公式（ 合式公式（wf.）的集合。

用下述三条归纳规则确定此集合 的集合 （i）对每一 i ≥ 1， pi是wf.。

（ii）若 A 和 B 是wf. ，则 (~ A)和 (A→B)是wf.。

（iii）所有的 wf. 是由（i）和（ii）产生的。

公理。

存在无穷多条公理，而借助于三条公理可以把所有的公理都指出来。

公理 对任意的wf. A,B,C,…，以下的 wf. 是L的公理： （L1）( A → (B→A) )。

（L2）( (A→(B→C)) → ((A→B)→(A→C)) )。

（L3）(((~A) →(~B)) → (B→A) )。

演绎规则。

分离规则（ MP）：从 A 和 (A→B ) ，得出 B 是一个直接后承， 演绎规则 这里 A 和 B 是 L 的任意 wf. 。

定义 2.2 在 L 中的一个证明是 wf. 的一个序列 A1,…,An，使得对每一 i (1≤i≤n), Ai 或者是 L 的 公理，或者是序列中在前的两个项，例如 Aj 和 Ak (j<i,k<i)，用演绎规则 MP 而得到 的一个直接后承。

这样的一个证明将称为 L 中 An 的证明 证明，而 An 称为 L 的定理 定理。

马琦 2010.9.4 maqi08@学习逻辑的目的之一：对推理过程的分析。

前一章：将语句和论证抽象到形式，并且对 一个有效的论证给出了直觉的定义。

本章：引进形式演绎系统的概念，本质上是 抽象过程的继续，从中概括出证明的概念。

形式系统符号字母表 合式公式：符号有穷串的集合 公理：某些合式公式的集合 演绎规则：可推出一个合式公式作为 合式公式有穷集的直接后承。

根据以上四点，就可以从公理出发， 使用推理规则依次完成演绎的过程。

系统元素（项） 运算符号字母表：~,→,( , ) , p1, p2, p3,… 合式公式（wf.）的集合。

用下述三条归纳规则确定此集合 （i）对每一 i ≥ 1， pi是wf.。

（ii）若 A 和 B 是wf. ，则 (~ A)和 (A→B)是wf.。

（iii）所有的 wf. 是由（i）和（ii）产生的。

公理。

存在无穷多条公理，而借助于三条公理可以把所有的公理都指出来。

对任意的wf. A,B,C,…，以下的 wf. 是L的公理：（L1）( A → (B→A) )。

（L2）( (A→(B→C)) → ((A→B)→(A→C)) )。

（L3）(((~A) →(~B)) → (B→A) )。

演绎规则。

分离规则（MP）：从 A 和 (A→B ) ，得出 B 是一个直接后承， 这里 A 和 B 是 L 的任意 wf. 。

定义 2.2 在 L 中的一个证明是 wf. 的一个序列 A1,…,An，使得对每一 i (1≤i≤n), Ai 或者是 L 的 公理，或者是序列中在前的两个项，例如 Aj 和 Ak (j<i,k<i)，用演绎规则 MP 而得到 的一个直接后承。

这样的一个证明将称为 L 中 An 的证明，而 An 称为 L 的定理。

例 2.4 下面的序列是 L 中的证明。

（1）(p1 →(p2→p1)) （2）(p1 →(p2→p1)) → ((p1→p2) → (p1→p1) ) ) （3）((p1→p2) → (p1→p1) ) 由此得出 ((p1→p2) → (p1→p1) ) 是 L 的定理。