2020届新高考数学模拟仿真卷(山东卷)第1卷

2020届新高考数学模拟仿真卷(山东卷)第1卷1、已知函数()f x =的定义域为M, ()g x =N,则M N I =（ ）A ．{}|2x x ≥-B ．{}|2x x <C ．{}|22x x -<<D ．{}|22x x -≤<2、已知复数2i1ia z +=-是纯虚数,则实数a =( )B.23、设,R a b ∈，那么“1ab>” 是“0a b >>” 的( ) A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件4、随机调查某校50个学生在学校的午餐费,结果如下表:这50个学生的午餐费的平均值和方差分别是（ ）A. 7.2,0.56B.C. 7,0.6D. 5、已知扇形的半径为2，面积为4，则这个扇形圆心角的弧度数为（ ）A.B. C. D. 26、已知()f x 是定义在[]10,10-上的奇函数,且()(4)f x f x =-,则函数()f x 的零点个数至少为( ) A.3B.4C.5D.67、已知圆22:(1)(1)1C x y -++=与直线10kx y ++=相交于,A B 两点,若CAB △为等边三角形,则2k 的值为( ) A.3B.4C.5D.68、如图，网格纸上小正方形的边长为1，粗线画出的是某四面体的三视图，则该四面体的外接球表面积为( )A.323πB. 32πC. 36πD. 48π9、函数()f x 的定义域为R ,且(1)f x +与(2)f x +都为奇函数,则( ) A.()f x 为奇函数 B.()f x 为周期函数 C.(3)f x +为奇函数D.(4)f x +为偶函数 10、关于多项式62(1)x x+-的展开式,下列结论正确的是( ) A.各项系数之和为1 B.各项系数的绝对值之和为122 C.存在常数项D.3x 的系数为4011、在ABC △中,,,a b c 分别是角,,A B C 的对边,C 为钝角,且2cos c b b A -=,则下列结论正确的是( ) A.2()a b b c =+B.2A B =C.10cos 2A <<D.10sin 2B <<12、在等腰梯形ABCD 中,已知1AB AD CD ===,2BC =,将ABD △沿直线BD 翻折成'A BD △,如图,则( )A.'A BD ∠为定值B.点A 的轨迹为线段C.直线'BA 与CD 所成的角的范围为ππ[,]32D.翻折过程中形成的三棱锥'A BCD -313、已知向量,a b r r的夹角为60︒,且1a b ==r r ,则a b +r r =__________.14、已知{}n a 为等差数列，n S 为其前n 项和．若13560a a a ＝，＋＝，则6S ＝__________. 15、已知双曲线22221(0,0)x y a b a b-=>>的左,右顶点分别为12,A A ,虚轴的上,下两个端点分别为12,B B ,若四边形1122A B A B 的内切圆面积为18π,则双曲线焦距的最小值为________. 16、设函数()(R)f x x ∈的导数为'(),(0)2020f x f =,且'()()2f x f x =-,则()f x =_________, ()40342'()f x f x +>的解集是________.17、设函数π()2cos()32x f x =-． （1）求()f x 的周期和单调增区间；（2）当[0,2π]x ∈时，求()f x 的最大值和最小值18、已知等差数列{}n a 满足3577,26a a a =+=,{}n a 的前n 项和为n S . （1）求n a 及n S ； （2）记12111...n nT S S S =+++，求n T19、如图，该几何体的三个侧面11AA B B ，11BB C C ，11CC A A 都是矩形.（1）证明：平面//ABC 平面111A B C ；（2）若12AA AC =，AC AB ⊥，M 为1CC 中点，证明：1A M ⊥平面ABM .20、某省高考改革实施方案指出:该省高考考生总成绩将由语文、数学、外语3门统一高考成绩和学生自主选择的学业水平等级性考试科目共同构成.该省教育厅为了解正就读高中的学生家长对高考改革方案所持的赞成态度,随机从中抽取了100名城乡家长作为样本进行调查,调查结果显示样本中有25人持不赞成意见.下面是根据样本的调查结果绘制的等高条形图.（1）根据已知条件与等高条形图完成下面的22⨯列联表,并判断我们能否有95％的把握认为“赞成高考改革方案与城乡户口有关”?（2）利用分层抽样从持“不赞成”意见家长中抽取5名参加学校交流活动，从中选派2名家长发言，求恰好有1名城镇居民的概率. 附：()()()()()22n ad bc K n a b c d a b c d a c b d -=⋅=+++++++21、设12F F ，分别是椭圆2222C:=1(a>b>0)x y a b+的左，右焦点，M 是C 上一点且2MF 与x轴垂直，直线1MF 与C 的另一个交点为N . （1）若直线MN 的斜率为34，求C 的离心率； （2）若直线MN 在y 轴上的截距为2，且15MN F N ＝，求.a b ，22、已知函数()()1ln 1f x x x =++，()ln 1x g x e x -=++ （1）讨论()f x 的单调性；（2）设()()()h x f x g x =-，若()h x 的最小值为M ，证明：2211M e e--<<-．答案以及解析1答案及解析： 答案：D解析：由题得到20x ->，即2x <， ∴{|2}M x x =<，由()g x =20x +…，即2x -…， ∴2{|}N x x =-…， 则2|}2{M N x x ⋂=-<….2答案及解析： 答案：B 解析：由22i (2i)(1i)(2)(2)i1i 1i 2a a a a z +++-++===--是纯虚数,得2a =,选B3答案及解析： 答案：C解析：由不等式的性质，0a b >>，可推出1ab>， 而当1ab>时，例如取2,1a b =-=-，显然不能推出0a b >>。

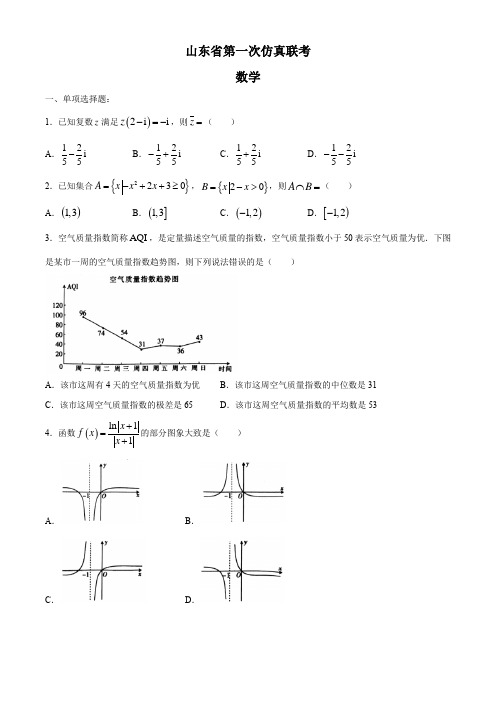
山东省第一次仿真联考数学一、单项选择题：1．已知复数z 满足()2i i z -=-，则z =（ ） A ．12i 55-B ．12i 55-+ C ．12i 55+D ．12i 55-- 2．已知集合{}2230A x x x =-++≥，{}20B x x =->，则A B ⋂=（ ） A ．()1,3B ．(]1,3C ．()1,2-D ．[)1,2- 3．空气质量指数简称AQI ，是定量描述空气质量的指数，空气质量指数小于50表示空气质量为优．下图是某市一周的空气质量指数趋势图，则下列说法错误的是（ ）A ．该市这周有4天的空气质量指数为优B ．该市这周空气质量指数的中位数是31C ．该市这周空气质量指数的极差是65D ．该市这周空气质量指数的平均数是534．函数()ln 11x f x x +=+的部分图象大致是（ ）A ．B ．C ．D ．5．已知:1p x a -<，3:11q x >+，若p 是q 的充分不必要条件，则a 的取值范围为（ ） A ．[]0,1B ．(]0,1C ．[)1,2-D ．()1,2-6．已知0a >，0b >，且320a b ab +-=，则3a b +的最小值是（ ） A ．6B ．8C ．12D ．167．踢毽子是中国民间传统的运动项目之一，起源于汉朝，至今已有两千多年的历史，是一项简便易行的健身活动某单位组织踢毽子比赛，把10人平均分成甲、乙两组，其中甲组每人在1分钟内踢毽子的数目分别为26，29，32，45，51；乙组每人在1分钟内踢毽子的数目分别为28，31，38，42，49．从甲、乙两组中各随机抽取1人，则这两人踢毽子的数目之和为奇数的概率是（ ） A ．59B ．49C ．1325D ．12258．已知()f x '是函数()f x 的导数，且()()f x f x -=，当0x ≥时，()3f x x '>，则不等式()()3132f x f x x --<-的解集是（ ）A ．1,02⎛⎫-⎪⎝⎭B ．1,2⎛⎫-∞-⎪⎝⎭C ．1,2⎛⎫+∞⎪⎝⎭D ．1,2⎛⎫-∞ ⎪⎝⎭二、多项选择题：9．已知函数()tan ,tan sin sin ,tan sin x x xf x x x x >⎧=⎨≤⎩，则（ ）A ．()f x 的值域为()1,-+∞B ．()f x 的单调递增区间为(),2k k k πππ⎡⎫+∈⎪⎢⎣⎭Z C ．当且仅当()2k x k k πππ-<≤∈Z 时，()0f x ≤D ．()f x 的最小正周期时2π10．已知奇函数()f x 是定义在R 上的减函数，且()21f =-，若()()1g x f x =-，则下列结论一定成立的是（ ） A ．()10g =B ．()122g =-C ．()()0g x g x -+>D ．()()110g x g x -+++<11．已知双曲线22221x y a b-=（0a >，0b >）的右焦点为()F ，点P 的坐标为（0，1），点Q 为双曲线C 左支上的动点，且PQF △的周长不小于14，则双曲线C 的离心率可能为（ ）AB ．CD ．312．一个正方体的平面展开图如图所示，在这个正方体中，点H 是棱DN 的中点，P ，Q 分别是线段AC ，BN （不包含端点）上的动点，则下列说法正确的是（ ）A ．在点P 的运动过程中，存在//HP BMB ．在点Q 的运动过程中，存在FQ AH ⊥C ．三棱锥H QAC -的体积为定值D ．三棱锥B PEM -的体积不为定值第Ⅱ卷三、填空题：13．已知向量(),2a m =，()1,3b =-，若a b ⊥，则a =______．14．五一放假期间，某社区安排甲、乙、丙、丁、戊这5位工作人员值班，每人值班一天，若甲排在第一若甲排在第一天值班，且丙与丁不排在相邻的两天值班，则可能的值班方式有______种．15．在四棱锥P ABCD -中四边形ABCD 是边长为2的正方形，PC PD ==平面PCD ⊥平面ABCD ，则四棱锥P ABCD -外接球的表面积为_______．16．已知抛物线():220C x py p =>的焦点为F ，斜率为1的直线l 过点F ，且与抛物线C 交于A ，B 两点，点M 在抛物线C 上，且点M 在直线l 的下方，若MAB △面积的最大值是，则抛物线C 的方程是_______，此时，点M 的坐标为_______． 四、解答题：17．在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ，在①1cos cos sin sin 2b A C a B C b =-；②1cos cos sin 2cos 2b B C c B B +=；③cos 2cos b A a c B+=这三个条件中任选一个，补充在下面问题中，并作答．已知D 是BC 上的一点，2BC BD AB =>，AD =6AB =，若_______，求ACD △的面积．注：如果选择多个条件分别解答，按第一个解答计分． 18．设数列{}n a 的前n 项和为n S ，且22n S n n =+．（1）求{}n a 的通项公式； （2）若11n nn n n a a b a a ++=+，求数列{}n b 的前n 项和n T ． 19．在斜三棱柱111ABC A B C -中，ABC △为等腰直角三角形，1AA ===，平面11BB C C ⊥⊥平面ABC ，点E 为棱1A A 的中点，160B BC ∠=︒．（1）证明：平面1B CE ⊥平面11BB C C ． （2）求二面角1A B C E --的余弦值．20．某公司采购了一批零件，为了检测这批零件是否合格，从中随机抽测120个零件的长度（单位：分米），按数据分成[]1.21.3，，(]1.3,1.4，(]1.4,1.5，(]1.5,1.6，(]1.6,1.7，(]1.7,1.8这6组，得到如图所示的频率分布直方图，其中长度大于或等于1.59分米的零件有20个，其长度分别为1.59，1.59，1.61，1.61，1.62，1.63，1.63，1.64，1.65，1.65，1.65，1.65，1.66，1.67，1.68，1.69，1.69，1.71，1.72，1.74，以这120个零件在各组的长度的频率估计整批零件在各组长度的概率．（1）求这批零件的长度大于1.60分米的频率，并求频率分布直方图中m ，n ，t 的值；（2）若从这批零件中随机选取3个，记X 为抽取的零件长度在(]1.4,1.6的个数，求X 的分布列和数学期望；（3）若变量S 满足()0.68260.05P S μσμσ-<≤+-≤且()220.95440.05P S μσμσ-<≤+-≤，则称变量S 满足近似于正态分布()2,N μσ的概率分布．如果这批零件的长度Y （单位：分米）满足近似于正态分布()1.5,0.01N 的概率分布，则认为这批零件是合格的将顺利被签收；否则，公司将拒绝签收．试问，该批零件能否被签收？21．在直角坐标系xOy 中已知()1,0F ，动点P 到直线6x =的距离等于22PF +动点P 的轨迹记为曲线C ．（1）求曲线C 的方程；（2）已知()2,0A ，过点F 的动直线l 与曲线C 交于B ，D 两点，记AOB △和AOD △的面积分别为1S 和2S ，求12S S +的最大值．22．已知函数()()ln f x x mx m =-∈R ． （1）讨论()f x 的单调性（2）若()f x 恰有两个不同的零点1x ，2x ，证明：()()120f x f x ''+>．山东省第一次仿真联考数学参考答案1．C 由题意可得：i i(2i)12i 2i (2i)(2i)55z --+===---+，则12i 55z =+． 2．D 由题意得[]1,3A =-，(),2B =-∞中，则[)1,2A B ⋂=-．3．B 由图可知该市这周空气质量指数的中位数、极差、平均数分别是43，65，53，有4天的空气质量指数小于50，故选B ．4．A 设()ln x g x x=，因为()()g x g x =-，所以()g x 的图象关于y 轴对称．所以()f x 的图象关于直线1x =-对称，排除C ．D ；当10x -<<时，ln 10x +<，所以()0f x <，排除B ，故选A ． 5．A 因为1x a -<，所以11a x a -<<+．即:11p a x a -<<+，因为311x >+，所以12x -<<，即:12q x -<<．因为p 是q 的充分不必要条件，所以1112a a -≥-⎧⎨+≤⎩，解得01a ≤≤．6．B 因为320b b a a +-=，所以312a b+=， 所以()()131133133106108222b a a b a b a b a b ⎛⎫⎛⎫+=++=++≥⨯+= ⎪ ⎪⎝⎭⎝⎭（当且仅当2a l ==时取等号）． 7．C 由题意可得所求概率1111332211551325C C C C P C C +==． 8．D 设()()232g x f x x =-，则()()3g x f x x ''=-．因为当0x ≥时，()3f x x '>，所以当0x ≥时，()0g x '>，即()g x 在[)0,+∞上单调递增．因为()()f x f x -=，所以()f x 为偶函数．则()g x 也是偶函数．因为()()3132f x f x x --<-，所以()()()22331122f x x f x x -<---，即()()1g x g x <-，则1x x <-，解得12x <． 9．AD 当tan sin x x >，即()2k x k k πππ<<+∈Z 时，()()tan 0,f x x =∈+∞；当tan sin x x ≤，即()2k x k k πππ-<≤∈Z 时，()()sin 1,1f x x =∈-．综上，()f x 的值域为()1,-+∞，故A 正确；()f x 的单调递增区间是2,222k k ππππ⎛⎫-+⎪⎝⎭和()32,22k k k ππππ⎛⎫++⎪⎝⎭∈Z ，B 错误；当()2,22x k k k ππππ⎛⎫∈++ ⎪⎝⎭∈Z 时，()0f x >，故C 错误；结合()f x 的图象可知()f x 的最小正周期是2π，故D 正确．10．AC 因为()f x 为定义在R 上的奇函数，所以()00f =，因为()()1g x f x =-，所以()()100g f ==，故A 正确；因为()f x 为定义在R 上的减函数，且()21f =-，()()()210f f f <<，即()110f -<<．所以()120g -<<，故B 不一定成立；因为()()1g x f x =-，所以()()()11g x f x f x -=--=-+，所以()()()()11g x g x f x f x -+=--+，因为()f x 是定义在R 上的减函数，所以()()11f x f x ->+，所以()()110f x f x +-->，即()()0g x g x -+>，故C 正确；因为()()1g x f x =-，所以()()()1g x f x f x -+=-=-，()()1g x f x +=，所以()()()()110g x g x f x f x -+++=-+=，选项D 错误．11．AC 设双曲线C 的左焦点为F '．则2QF QF a '-=．即2QF QF a '=+，故22QF PQ QF PQ a PF a ''+=++≥+．由题意可得5PF PF '===，所以2214PQ QF PF PF a +≥+≥+，所以2a ≥．则双曲线C 的离心率c e a ==≤因为1e >．所以双曲线C 的离心率的取值范围为(．12．BC 由平面展开图，还原正方体，如图所示．对于A 选项，因为点P 是线段AC 上的动点，所以HP ⊂平面ACH ，因为BM ⊄平面ACH ，且BM 与平面ACH 不平行，所以不存在//HP BM ．故A 错误；对于B 选项．连接BD ，BD AC O ⋂=，连接OF ，OF BN G ⋂=，取AD 的中点K ，连接EK ，OK ．则O 为BD 的中点，//OK EF ，所以E ，F ，O ，K 四点共面，因为AH EK ⊥，AH EF ⊥，所以AH ⊥平面EFOK ，因为GF ⊂平面EFOK ，所以AH GF ⊥，即当点Q 运动到G 点时，FQ AH ⊥，故B 正确；对于C 选项，因为点H 是棱DN 的中点，所以//OH BN ，因为OH ⊂平面ACH ，BN ⊄平面ACH ，所以//BN 平面ACH ，则直线BN 上的任意一点到平面ACH 的距离相等，且为定值，因为点Q 是线段BN 上的动点，所以点Q 到平面ACH 的距离d 为定值，因为ACH △的面积为定值，所以13H QW Q WH ACH V V d S --⋅==△（定值），故C 正确；对于D 选项，因为点P 是线段AC 上的动点。

山东省第一次仿真联考数学一、单项选择题：1. 已知复数z 满足()2z i i -=-，则z =( ) A.1255i - B. 1255i -+ C.1255i + D. 1255i -- 【答案】C 【解析】 【分析】 由已知可求出2i z i -=-，结合复数的除法运算对其进行整理得1255z i =-，从而可求出共轭复数. 【详解】解：由题意可得：(2)122(2)(2)55i i i z i i i i --+===---+，则1255z i =+. 故选:C.【点睛】本题考查了复数的除法运算，考查了共轭复数的求解.本题的关键是对z 进行整理变形. 2. 已知集合{}2230A x x x =-++≥，{}20B x x =->，则A B =( )A. ()1,3B. (]1,3C. ()1,2-D. [)1,2-【答案】D 【解析】 【分析】先解不等式得集合A,B ，再根据交集概念求结果. 【详解】由题意得[]1,3A =-，(),2B =-∞中，则[)1,2A B =-.故选：D【点睛】本题考查集合交集运算、一元二次不等式解集，考查基本分析求解能力，属基础题.3. 空气质量指数简称AQI ，是定量描述空气质量的指数，空气质量指数小于50表示空气质量为优.下图是某市一周的空气质量指数趋势图，则下列说法错误的是( )A. 该市这周有4天的空气质量指数为优B. 该市这周空气质量指数的中位数是31C. 该市这周空气质量指数的极差是65D. 该市这周空气质量指数的平均数是53【答案】B 【解析】 【分析】由图可知该市这周空气质量指数，从而可计算平均数，中位数，极差，即可选出正确答案. 【详解】解：由图可知该市这周空气质量指数为96,74,54,31,37,36,43，则 平均数为()196745431373643537⨯++++++=，有4天的空气质量指数小于50， 按大小排列为31,36,37,43,54,74,96，则中位数为43，极差为963165-= 故选:B.【点睛】本题考查了数据分析，考查了平均数的求解，考查了中位数的求解，考查了极差的求解. 4. 函数ln |1|()|1|x f x x +=+的部分图象大致是（ ）A. B.C. D.【答案】A 【解析】 【分析】由()f x 的图象关于直线1x =-对称，排除C 、D ；当10x -<<时，ln |1|0x +<，所以()0f x <，排除B. 【详解】设ln ||()||x g x x =， 因为()()g x g x =-，所以()g x 的图象关于y 轴对称.所以()f x 的图象关于直线1x =-对称，排除C 、D ； 当10x -<<时，ln |1|0x +<， 所以()0f x <，排除B . 故选：A .【点睛】本题主要考查了利用函数解析式求解图像的问题，解决本类题时，通常是利用函数的单调性、奇偶性、函数值等排除选项.属于较易题 5. 已知:1p x a -<，3:11q x >+，若p 是q 的充分不必要条件，则a 的取值范围为( ) A. []0,1 B. (]0,1C. [)1,2-D. ()1,2-【答案】A 【解析】 【分析】解绝对值不等式和分式不等式对命题进行化简，依据二者的关系可得1112a a -≥-⎧⎨+≤⎩，即可求出a 的取值范围.【详解】解：因为1x a -<，所以11a x a -<<+.即:11p a x a -<<+， 因为311x >+，所以12x -<<，即:12q x -<<. 因为p 是q 的充分不必要条件，所以1112a a -≥-⎧⎨+≤⎩，解得01a ≤≤.故选:A.【点睛】本题考查了已知命题关系求参数的取值范围，考查了绝对值不等式的求解，考查了分式不等式的求解.本题的关键是对命题进行化简.6. 已知0a >，0b >，且320a b ab +-=，则3a b +的最小值是( ) A. 6B. 8C. 12D. 16【答案】B 【解析】 【分析】先化简条件得312a b+=，再利用1的代换以及基本不等式求最值即可. 【详解】因为0a >，0b >，320a b ab +-=，所以312a b+=，所以()()1311331133101061082222b a a b a b a b a b ⎛⎫⎛⎫⎛⎫+=++=++≥=⨯+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ （当且仅当2a b ==时取等号）. 故选：B【点睛】本题考查利用基本不等式求最值，考查基本分析求解能力，属基础题.7. 踢毽子是中国民间传统的运动项目之一，起源于汉朝，至今已有两千多年的历史，是一项简便易行的健身活动.某单位组织踢毽子比赛，把10人平均分成甲、乙两组，其中甲组每人在1分钟内踢毽子的数目分别为26，29，32，45，51；乙组每人在1分钟内踢毽子的数目分别为28，31，38，42，49.从甲、乙两组中各随机抽取1人，则这两人踢毽子的数目之和为奇数的概率是( ) A.59B.49C.1325D.1225【答案】C 【解析】 【分析】先确定从甲、乙两组中各随机抽取1人总事件数，再确定抽取两人踢毽子的数目之和为奇数所包含事件数，最后根据古典概型概率公式求解.【详解】从甲、乙两组中各随机抽取1人有5525⨯=种取法； 其中抽取两人踢毽子的数目之和为奇数有223313⨯+⨯=种取法； 从而所抽两人踢毽子的数目之和为奇数的概率是1325故选：C【点睛】本题考查古典概型概率，考查基本分析求解能力，属基础题.8. 已知()f x '是函数()f x 的导数，且()()f x f x -=，当0x ≥时，()3f x x '>，则不等式()()3132f x f x x --<-的解集是（ ）A .1,02⎛⎫-⎪⎝⎭B. 1,2⎛⎫-∞-⎪⎝⎭C. 1,2⎛⎫+∞⎪⎝⎭D. 1,2⎛⎫-∞ ⎪⎝⎭【答案】D 【解析】 【分析】构造函数()()232g x f x x =-，根据条件确定其单调性与奇偶性，化简不等式()()3132f x f x x --<-为()()1g x g x <-，再根据单调性与奇偶性转化不等式为1x x <-，解得结果.【详解】设()()232g x f x x =-，则()()3g x f x x ''=-. 因为当0x ≥时，()3f x x '>，所以当0x ≥时，()()30g x f x x ''=->，即()g x 在[)0,+∞上单调递增. 因为()()f x f x -=，所以()()()()223322g x f x x f x x g x -=--=-=， 所以()g x 是偶函数. 因为()()3132f x f x x --<-，所以()()()22331122f x x f x x -<---，即()()1g x g x <-，()()|||1|g x g x ∴<-，则1x x <-，解得12x <. 故选：D【点睛】本题考查了构造函数解决导数问题，考查了利用导数研究函数的单调性，考查了利用函数的奇偶性和单调性解不等式，属于中档题.二、多项选择题：9. 已知函数()tan ,tan sin sin ,tan sin x x xf x x x x >⎧=⎨≤⎩，则( )A. ()f x 值域为()1,-+∞B. ()f x 的单调递增区间为(),2k k k πππ⎡⎫+∈⎪⎢⎣⎭Z C. 当且仅当()2k x k k πππ-<≤∈Z 时，()0f x ≤D. ()f x 的最小正周期时2π【答案】AD 【解析】 【分析】根据三角函数的性质可得当()2k x k k πππ<<+∈Z 时，()tan f x x =，当()2k x k k πππ-<≤∈Z 时，()sin f x x =，结合图象逐一判断即可. 【详解】当tan sin x x >，即()2k x k k πππ<<+∈Z 时，()()tan 0,f x x =∈+∞；当tan sin x x ≤，即()2k x k k πππ-<≤∈Z 时，()()sin 1,1f x x =∈-.综上，()f x 的值域为()1,-+∞，故A 正确；()f x 的单调递增区间是2,222k k ππππ⎛⎫-+ ⎪⎝⎭和()32,22k k k ππππ⎛⎫++ ⎪⎝⎭∈Z ，B 错误；当()2,22x k k k ππππ⎛⎫∈++ ⎪⎝⎭∈Z 时，()0f x >，故C 错误；结合()f x 的图象可知()f x 的最小正周期是2π，故D 正确. 故选：AD.【点睛】本题主要考查了三角函数的性质，得出函数()f x 的解析式是解题的关键，属于中档题. 10. 已知奇函数()f x 是定义在R 上的减函数，且(2)1f =-，若()(1)g x f x =-，则下列结论一定成立的是（ ） A. (1)0g =B. 1(2)2g =-C. ()()0g x g x -+>D. (1)(1)0g x g x -+++<【答案】AC 【解析】 【分析】根据奇函数性质得(0)0f =，即得(1)g ，可判断A; (2)(1)g f =，根据单调性可得1(1)0f -<<，即可判断B;先根据定义以及奇函数性质得()()(1)(1)g x g x f x f x -+=--+，再根据函数()f x 单调性判断C; 根据定义以及奇函数性质得(1)(1)()()0g x g x f x f x -+++=-+=，即可判断D. 【详解】因为()f x 为定义在R 上的奇函数，所以(0)0f =，因为()(1)g x f x =-， 所以(1)(0)0g f ==，故A 正确；因为()f x 为定义在R 上的减函数，且(2)1f =-，(2)(1)(0)f f f <<， 即1(1)0f -<<.所以1(2)0g -<<，故B 不一定成立； 因为()(1)g x f x =-，所以()(1)(1)g x f x f x -=--=-+，所以()()(1)(1)g x g x f x f x -+=--+，因为()f x 是定义在R 上的减函数，所以(1)(1)f x f x ->+，所以(1)(1)0f x f x --+>，即()()0g x g x -+>，故C 正确； 因为()(1)g x f x =-，所以(1)()()g x f x f x -+=-=-，(1)()g x f x +=， 所以(1)(1)()()0g x g x f x f x -+++=-+=，选项D 错误. 故选：AC【点睛】本题考查函数奇偶性以及单调性应用，考查基本分析判断能力，属中档题.11. 已知双曲线22221x y a b-=（0a >，0b >）的右焦点为()F ，点P 的坐标为（0，1），点Q 为双曲线C 左支上的动点，且PQF △的周长不小于14，则双曲线C 的离心率可能为( )B. D. 3【答案】AC 【解析】 【分析】根据双曲线的定义，将PQF △的周长的最小值转化为求QF PQ '+的最小值，即可求出离心率的范围，观察选项即可判断.【详解】设双曲线C 的左焦点为F ',则2QF QF a '-=,即2QF QF a '=+，故22QF PQ QF PQ a PF a ''+=++≥+.由题意可得2415PF PF '==+=，所以2214PQ QF PF PF a +≥+≥+，所以2a ≥.则双曲线C 的离心率266c e a ==≤.因为1e >.所以双曲线C 的离心率的取值范围为(1,6⎤⎦. 故选：AC【点睛】本题主要考查双曲线的定义、离心率及一动点到两定点的距离之和的最小值，属于基础题. 12. 一个正方体的平面展开图如图所示，在这个正方体中，点H 是棱DN 的中点，P ，Q 分别是线段AC ，BN （不包含端点）上的动点，则下列说法正确的是( )A. 在点P 的运动过程中，存在//HP BMB. 在点Q 的运动过程中，存在FQ AH ⊥C. 三棱锥H QAC -的体积为定值D. 三棱锥B PEM -的体积不为定值 【答案】BC 【解析】 【分析】由异面直线的判断方法，可判断A ；运用线面垂直的判断与性质定理可判断B ；由棱锥的体积公式和线面距离与点面距离的关系，可判断C ，D ．【详解】解：由平面展开图，还原正方体，如图所示.对于A 选项，因为点P 是线段AC 上的动点，所以HP ⊂平面ACH ，因为BM ⊄平面ACH ，且BM 与平面ACH 不平行，所以不存在//HP BM .故A 错误； 对于B 选项.连接BD ，BD AC O ⋂=，连接OF ，OF BN G ⋂=，取AD 的中点K ，连接EK ，OK .则O 为BD 的中点，//OK EF ，所以E ，F ，O ，K 四点共面，因为AH EK ⊥，AH EF ⊥，所以AH ⊥平面EFOK ，因为GF ⊂平面EFOK ，所以AH GF ⊥，即当点Q 运动到G 点时，FQ AH ⊥，故B 正确；对于C 选项，因为点H 是棱DN 的中点，所以//OH BN ，因为OH ⊂平面ACH ，BN ⊄平面ACH ，所以//BN 平面ACH ，则直线BN 上的任意一点到平面ACH 的距离相等，且为定值，因为点Q 是线段BN 上的动点，所以点Q 到平面ACH 的距离d 为定值，因为ACH 的面积为定值，所以13H QW Q WH ACH V V d S --⋅==△（定值），故C 正确；对于D 选项，因为点P 是线段AC 上的动点。

2020年2020届山东省高三高考模拟考试数学试卷★祝考试顺利★ (解析版)一、单项选择题：1.已知集合{1,2}A =-,{|1}B x ax ==,若B A ⊆,则由实数a 的所有可能的取值组成的集合为（ ）A. 11,2⎧⎫⎨⎬⎩⎭B. 11,2⎧⎫-⎨⎬⎩⎭C. 10,1,2⎧⎫⎨⎬⎩⎭D. 11,0,2⎧⎫-⎨⎬⎩⎭【答案】D 【解析】分B 为空集和B 不为空集两种情况讨论,分别求出a 的范围,即可得出结果. 【详解】因为集合{1,2}A =-,{|1}B x ax ==,B A ⊆, 若B 为空集,则方程1ax =无解,解得0a =； 若B 不为空集,则0a ≠；由1ax =解得1x a=,所以11a =-或12a =,解得1a =-或12a =,综上,由实数a 的所有可能的取值组成的集合为11,0,2⎧⎫-⎨⎬⎩⎭.故选D2.若1iz i =-+（其中i 是虚数单位）,则复数z 的共轭复数在复平面内对应的点位于( ) A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限【答案】D分析：变形1iz i =-+,利用复数代数形式的乘除运算化简,求出z 的坐标即可得结论. 详解：由i 1i z =-+, 得()()21i i 1i 1i i iz -+--+===+-,1z i =- ∴复数z 的共轭复数在复平面内对应的点的坐标为()1,1-,位于第四象限,故选D.3.函数()()22ln x xf x x -=+的图象大致为（ ）A. B.C. D.【答案】B 【解析】根据函数奇偶性的判断可知函数为偶函数,图象关于y 轴对称,排除D ；根据()0,1x ∈时,()0f x <,排除,A C ,从而得到正确选项. 【详解】()f x 定义域为{}0x x ≠,且()()()()22ln 22ln x x x x f x x x f x ---=+-=+=()f x ∴为偶函数,关于y 轴对称,排除D ；当()0,1x ∈时,220x x -+>,ln 0x <,可知()0f x <,排除,A C . 本题正确选项：B4.《九章算术⋅衰分》中有如下问题:“今有甲持钱五百六十,乙持钱三百五十,丙持钱一百八十,凡三人俱出关,关税百钱.欲以钱数多少衰出之,问各几何?”翻译为“今有甲持钱560,乙持钱350,丙持钱180,甲、乙、丙三个人一起出关,关税共计100钱,要按个人带钱多少的比例交税,问三人各应付多少税?”则下列说法中错误的是（ ） A. 甲付的税钱最多 B. 乙、丙两人付的税钱超过甲 C. 乙应出的税钱约为32 D. 丙付的税钱最少【答案】B 【解析】通过阅读可以知道,A D 说法的正确性,通过计算可以知道,B C 说法的正确性.【详解】甲付的税钱最多、丙付的税钱最少,可知,A D 正确:乙、丙两人付的税钱占总税钱的3511002<不超过甲。

山东省2020年普通高等院校统一招生模拟考试高三教学质量检测数学试题2020．02本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分，将第I 卷选择题的正确答案选项填涂在答题卡相应位置上，考试结束，将答题卡交回．考试时间120分钟，满分150分． 注意事项：1．答卷前，考生务必将姓名、座号、准考证号填写在答题卡规定的位置上． 2．第I 卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；如需改动，用橡皮擦干净后，再选涂其它答案标号．答案不能答在试题卷上．3．第Ⅱ卷答案必须写在答题卡各题目指定区域内相应的位置，不能写在试题卷上；如需改动，先划掉原来的答案，然后再写上新的答案；不准使用涂改液、胶带纸、修正带．不按以上要求作答的答案无效．第I 卷(选择题 共60分)一、选择题：(本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知复数2,i z z 在复平面内对应的点分别为()()11221,1,0,1z Z Z z =，则 A ．1i +B ．1i -+C ．1i --D ．1i -2．设a R ∈，则“sin cos αα=”是“sin 21α=”的 A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件D ．既不充分也不必要条件3．向量a b r r ，满足()()1,2a b a b a b ==+⊥-u u r u u r r r r r，则向量a b r r 与的夹角为 A ．45oB ．60oC ．90oD ．120o4．已知数列{}n a 中，372,1a a ==．若1n a ⎧⎫⎨⎬⎩⎭为等差数列，则5a = A ．23B ．32C ．43D ．345．已知点()2,4M 在抛物线()2:20C y px p =>上，点M 到抛物线C 的焦点的距离是A ．4B ．3C ．2D ．16．在ABC ∆中，2,20AB AC AD AE DE EB x AB y AC +=+==+u u u r u u u r u u u r u u u r u u u r u u u r u u u r u u u r，若，则 A ．2y x =B ．2y x =-C ．2x y =D ．2x y =-7．已知双曲线()2222:1,0,0x y C a b a b-=>>的左、右焦点分别为12,F F O ，为坐标原点，P是双曲线在第一象限上的点，()21212=2=2,0,PF PF m m PF PF m >⋅=u u u u r u u u u r u u u r u u u u r ，则双曲线C 的渐近线方程为 A ．12y x =±B ．22y x =±C ．y x =±D ．2y x =±8．已知奇函数()f x 是R 上增函数，()()g x xf x =则A. 233231log 224g g g --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭B ．233231log 224g g g --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C. 23323122log 4g g g --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭D. 23323122log 4g g g --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭二、多项选择题：本题共4小题，每小题5分，共20分。

按秘密级事项管理★启用前2020年普通高等学校招生全国统一考试(模拟卷)数学注意事项：1.答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。

2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3.考试结束后，将本试卷和答题卡一并交回。

一、单项选择题：本题共8小题，每小题5分，共40分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.设集合A = {(x t y)\x + y = 2}, B = {(x t y)\y = x2} t则AC\B =A. {(1,1)}B. {(-2,4)}C. {(1,1), (-2,4)}D. 02.己知a + bi (a t beR)是的共轭复数，则a + b =l + i-1数学试题第1页(共5页)C.有的正方形不是平行四边形D.不是正方形的四边形不是平行四边形8. ^a>b>c>\5.ac<b 2,贝lj A. log o b > log fc c > log c aC. log^>log a Z>>log c a二、多:页选择题：本题共4小题.毎小题5分，共20分。

在每小题给出的选项中，有 多项符合题目要求。

全部选对的得5分，部分选对的得3分，有选错的得0分。

9. 下图为某地区2006年〜2018年地方财政预算内收入、城乡居民储蓄年末余额折线 图.城乡居民储番年末 余额（百亿元） 地方财政预算内 收入（百亿元）根据该折线图可知，该地区2006年〜2018年A. 财政预算内收入、城乡居民储蓄年末余额均呈増长趋势B. 财政预算内收入、城乡居民储蓄年末余额的逐年增长速度相同C. 财政预算内收入年平均增长里髙于城乡居民储蓄年末余额年平均增长量D. 城乡居民储蓄年末余额与财政预算内收入的差额逐年增大10. 己知双曲线C 过点G.V2）且渐近线为y = ±^-x t 则下列结论正确的是A. C 的方程为—-/ = 13 B . c 的离心率为75C. 曲线y = e x -2-l 经过C 的一个焦点D. 直线x-^j-l = 0与C 有两个公共点11. 正方体ABCD-A^C.D.的棱长为丨，E, F ，G 分别为，CC,, 的中点.则A. 直线与直线垂直B. 直线冷G 与平面平行qC. 平面截正方体所得的截面面积为3 OD. 点C 与点G 到平面的距离相等数学试题第2页（共5页）B log c b ■> log,, a > log a c D. log ft a>log c Z>>log a e80706050403020100小B12.函数/(x)的定义域为R，且/(x + 1)与/Cr + 2)都为奇函数，则A. /(x)为奇函数 B. /(x)为周期函数C. /(x + 3)为奇函数D. /(x + 4)为偶函数三、填空题：本题共4小题，每小题5分，共20分。

山东省2020年高考数学模拟考试试题及答案按珈密级苇项管理*启用前2020年普通高等学校招生全国统一考试（模拟卷）数学asw 项：1. 答卷前，考生务必将口己的姓名、考生号等填遞在答题卡和试卷指定位匿匕工回答选择题时，选岀每小题答案屁用铅抠把答题R上对应题冃的答案折号涂熾如磁动,用橡皮掠干净后，再选涂苴他答案标号*回答非选择题时，将答案写在答题卡上。

另在本试卷上无效，生考试结束存*将本试卷和答題卡…井交回。

—、单项选择题：本趣共$小舐每小題§分・共豹分。

在每小题给出的四个选琐中，只有一项是符合髒目要求的“1, 迎集合/訂（工』）ix+?=2｝, 则*n七A. ｛（ij）｝氐｛（一签4）｝ C HM）J-2f4）｝6 02. 已知◎牛bi⑷b左R）是上二的共扳复数・则a^b =1 +1A- -1 B.-丄C- ；D・ 12 23* Bt向fi4-（.1,1）t A = c»（2,!）> 且（■-几血）丄―则丄“A. 3 氐2 G -2-34. 幵式中『抽系数足xA.-210B. -12QC. 120D. 2105+已知三按锥$_仙C中，ZSAB = ZABC= y * 5^-4• SC = 1J\3. XB = 2,5C = 6, 则三棱锥S 亠ABC的体积是A. 4B. 6 G 4巧D+ M6. 己知点丄为曲纯y二工+毀工:>0）上前动点，月为圆2F +/=!上的动点’则皿鋼X的最小值是九3 B•斗G迈 D. 4^27, 设命題戸所有正方形都是平行叫边母*则「卩为d所宿疋方形罰不長平行四边形B-有的平行四边底不是正方舷C”有的iE方形不是平行四边形 D.不是正方形的四边彫不是平行四边形数学试题第1页：（共5贡）数学试題第2页（共5页〉数学试題第2页（共5页〉8. 若>1 且 MC F ・则4. log 」、1隅疋、teg 評 C. log f c> lo£fl 5> lo 空 a二、多項远择题*本题共4」卜駆•毎小题5^-共20分・存毎小额给岀的选项中、右 多项精合倾目蓉求，全部选对的得5分，部分选对的得3分，有选措的得0分“ 9. 下国为茱地桜2006年〜2018年地方財政预算内收入、城乡居民储齧年未余额折线2财政预篇内收入*城乡居民储蓄年朮余额肉呈増怅趋势 R.财政预算内收入、城乡居民储蓄年末余额的逐年增长速度相同C. 赃政预畀内收入年平均增长虽局于城乡居民储蔷年末余额年平均增机帚 D, 城乡居艮储蓄年末余鈿与财政预算内收入的差報逐年增大w.已知艰曲线＜?过点Q 品且渐近钱为丿=±¥厂则下列结论正确的是A, C 的方程为■- / -I B ・0的离心翠为J5 C ・曲线经过C 的一于焦点 D.直线"逅厂1“与C 有两个公共点11正方陣」肌也GO 的梭长为1・E , F 、（?分别为5C, CC 「1?鸟的中点•则扎直线与直线曲垂直 B.直^Afi 与平面*防平行C 平面/EF 截正方体所得的載画面积为? D.点C?与点石到平而*EF 曲聊离相諄B- log"〉k 唱』a lug/ D, log/A 】0£ 占 > log/城乡尿民储雷叶朿 ♦余额C 百亿元】 亠地方财政预算内 收入f 百亿元）根据该折线I ］可Sb 该地区2006年-2018年\2.函数/(巧的定义域为K, fi7(^ + 1) f(x^2)都为奇函数，则A. 奇函数氐/V)为周期雷数C /(x + 3)为奇函数 D. /(I +4)X J®^I数三填空駆本题共4小题、每小题3分，共20分。