下载文档原格式
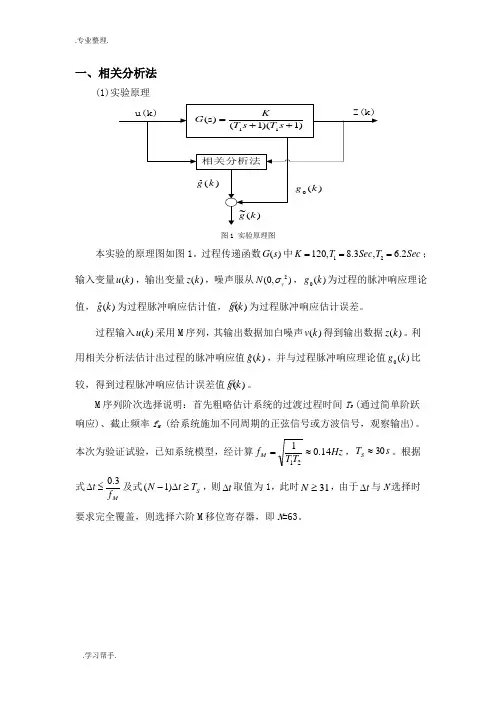
一、相关分析法(1)实验原理图1 实验原理图本实验的原理图如图1。
过程传递函数()G s 中12120,8.3, 6.2K T Sec T Sec ===；输入变量()u k ，输出变量()z k ，噪声服从2(0,)v N σ，0()g k 为过程的脉冲响应理论值，ˆ()g k 为过程脉冲响应估计值，()g k %为过程脉冲响应估计误差。
过程输入()u k 采用M 序列，其输出数据加白噪声()v k 得到输出数据()z k 。
利用相关分析法估计出过程的脉冲响应值ˆ()g k ，并与过程脉冲响应理论值0()g k 比较，得到过程脉冲响应估计误差值()g k %。
M 序列阶次选择说明：首先粗略估计系统的过渡过程时间T S (通过简单阶跃响应)、截止频率f M (给系统施加不同周期的正弦信号或方波信号，观察输出)。
本次为验证试验，已知系统模型，经计算Hz T T f M 14.0121≈=，s T S 30≈。
根据式Mf t 3.0≤∆及式S T t N ≥∆-)1(，则t ∆取值为1，此时31≥N ，由于t ∆与N 选择时要求完全覆盖，则选择六阶M 移位寄存器，即N =63。
(2)编程说明图2 程序流程图(3)分步说明 ① 生成M 序列：M 序列的循环周期63126=-=N ，时钟节拍1t Sec ∆=，幅度1a =，移位寄存器中第5、6位的内容按“模二相加”，反馈到第一位作为输入。
其中初始数据设为{1,0,1,0,0,0}。
程序如下：过程仿真得到理论输出数据()z k计算脉冲响应估计值计算互相关函数，得到脉冲响应估计值计算脉冲响应估计误差计算脉冲响应理论值，得到脉冲响应估计误差人机对话噪声标准差：sigma ；生成数据周期数：r生成数据生成M 序列()u k ；生成白噪声序列()v k② 生成白噪声序列： 程序如下：③ 过程仿真得到输出数据：如图2所示的过程传递函数串联，可以写成形如121211()1/1/K G s TT s T s T =++，其中112KK TT =。
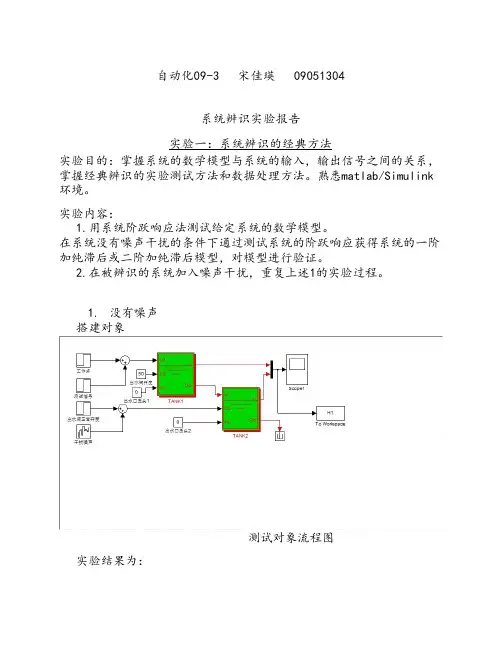
实验报告--实验1.基于matlab的4阶系统辨识实验课程：系统辨识题目：基于matlab的4阶系统辨识实验作者：专业：自动化学号：11351014目录实验报告 (1)1.引言 (2)2.实验方法和步骤 (2)3.实验数据和结果 (2)4.实验分析 (4)1、 引言系统辨识是研究如何确定系统的数学模型及其参数的理论。
而模型化是进行系统分析、仿真、设计、预测、控制和决策的前提和基础。
本次实验利用matlab 工具对一个简单的4阶系统进行辨识，以此熟悉系统辨识的基本步骤，和matlab 里的一些系统辨识常用工具箱和函数。
这次实验所采取的基本方法是对系统输入两个特定的激励信号，分别反映系统的动态特性和稳态特性。
通过对输入和输出两个系统信号的比较，来验证系统的正确性。
2、 实验方法和步骤2.1 实验方法利用matlab 对一个系统进行辨识，选取的输入信号必须能够反映系统的动态和稳态两个方面的特性，才能更好地确定系统的参数。
本次实验采取了两种输入信号，为反映动态特性，第一个选的是正弦扫频信号，由下面公式产生：选定频率范围 ，w(t)是时间t 的线性函数，具有扫频性质，可以反映系统的动态特性。
为反映稳态特性，选的输入信号是阶跃信号。
以上的到两组数据，利用matlab 的merge()函数，对两组数据融合，然后用matlab 系统辨识工具箱中的基于子空间方法的状态空间模型辨识函数n4sid()来对系统进行辨识2.2 实验步骤(1)建立一个4阶的线性系统，作为被辨识的系统，传递函数为3243211548765()125410865s s s G s s s s s -+-+=++++(2)产生扫频信号u1和阶跃信号u2(3)u1、u2作为输入对系统进行激励，分别产生输出y1和y2 (4)画出稳态测试输入信号u1-t 的曲线，和y1-t 的曲线 画出动态测试输入信号u2-t 的曲线，和y2-t 的曲线(5)使用merge()函数对u1-y1数据和u2-y2数据进行融合，并使用n4sid()函数对系统进行辨识。
《系统辨识》课程报告题目：最小二乘参数估计法班级：工控08.1姓名：学号：日期：2011.6.1成都信息工程学院控制工程学院最小二乘参数估计摘要：最小二乘法提供了一个估算方法，使之能得到一个在最小方差意义上与实验数据最好拟合的数学模型。
最小二乘的一次性完成辨识算法，他的特点是直接利用已经获得的观测数据进行运算处理。
求出一个使各次实际观测和计算值之间的差值的平方乘以度量其精度的数值以后的和为最小的数值，求出带辨识参数。
最小二乘辩识方法在系统辩识领域中先应用上已相当普及，方法上相当完善，可以有效的用于系统的状态估计，参数估计以及自适应控制及其他方面。
关键词：最小二乘法，AIC 准则，M 序列1 引言：最小二乘法是 1795 年高斯在预测星体运行轨道最先提出的 , 它奠定了最小二乘估计理论的基础 . 到 20 世纪 60 年代瑞典学者 Austron 把这个方法用于动态系统的辨识中 , 在这种辨识方法中 , 首先给出模类型 , 在该类型下确定系统模型的最优参数 .这种具有格式规范的辨识方法可以演绎成递推形式 .递推最小二乘算法计算量小 , 可以用于在线辨识 , 即使辨识对象随时间发生化 , 模型也可以对其进行跟踪断地进行更新和修正辨识参数 , 从而成为一种被广泛采用的辨识方法，最小二乘法有一次完成算法和递推算法，其中 一次完成算法存在一定的局限性，工业系统辨识常采用递推算法进行系统辨识。
2 实验原理：由于运用最小二乘一次完成算法进行系统参数辨识的时候，存在一定的限定条件，并且需要用到全部的观测数据，每采样一次就需要增添一组新的观察数据，所以引入递推最小二乘法来辨识系统参数，递推最小二乘法是用旧的估计值加上修正值得到的新的估计值，用新的测量数据对上一次的估计结果进行修正，直到估计值达到需要的精度为止。
2.1根据汉格尔矩阵估计模型的阶次设一个可观可控的SISO 过程的脉冲响应序列为{个g(1),g(2),……g(L)},可以通过汉格尔（Hankel ）矩阵的秩来确定系统的阶次。
系统的数学建模与辨识实验报告编号：8姓名：学号： 1电加热炉动态特性辨识实验报告一．实验目的通过实验了解辨识方法在工程应用中的一些实际问题；了解数据获取和数据处理的各种方法和手段，掌握各种辨识方法的应用特点。
二．实验内容1.数据获取按照电加热计算机控制系统使用说明，加热温箱并实时监测温度。
当温度升高到一定高度基本不再发生变化时，加入辨识信号。
本设计辨识信号采用伪随机二维序列中的M序列，由于设计的M序列过长，从中截取部分作为辨识信号。
设定辨识信号的采样周期和整个辨识信号循环次数，加入辨识信号记录温度随电压变化的数据结果。
2.数据处理观察实验数据，可发现扰动较严重，需要对数据进行预处理以便进行后续辨识。
对采集数据进行滤波等处理，实验输入为M序列长度为30，由于实际采集周期为2秒，所得数据远大于需要用到的数据，同时为了提高精度，减少扰动因素影响，数据处理过程中，当输入一个M序列元素后，采集到的数据中取最后5个数据求其平均作为该输入的输出结果。
数据处理最终结果为30组输入和输出，将其生成为.mat文件以供后续离线辨识使用。
3.离线辨识利用处理过的数据选择某种辨识方法进行参数估计，并判断阶次及迟滞。
辨识完成后，进行模型验证。
三．实验操作1．设定相关实验参数，启动试验设备。
本实验设置的加热电压为60V，温度采样间隔为2s，开始实验，加热温箱系统，并通过客户端软件实时观察温箱温度，并记录，等待温箱温度升高到一定高度不再有明显上升变化。
2. 设计辨识信号考虑到实验加热电压为60V，整个系统的加热电压为之前设置的系统加热电压与辨识信号电压的和，为了在较短时间内也能产生一定的变化，辨识电压值不宜过小，选取辨识信号电压为10V 。
此时，加入辨识信号后的整个系统电压在50V 和70V 来回跳动。
辨识序列采用M 序列，并使用庞中华系统辨识程序中的M 序列生成程序，序列长度设置为31，结果如下图所示：3. 当第一步的温箱电压升高到一定高度，不再有明显升上变化时，便可认为系统已经稳定。
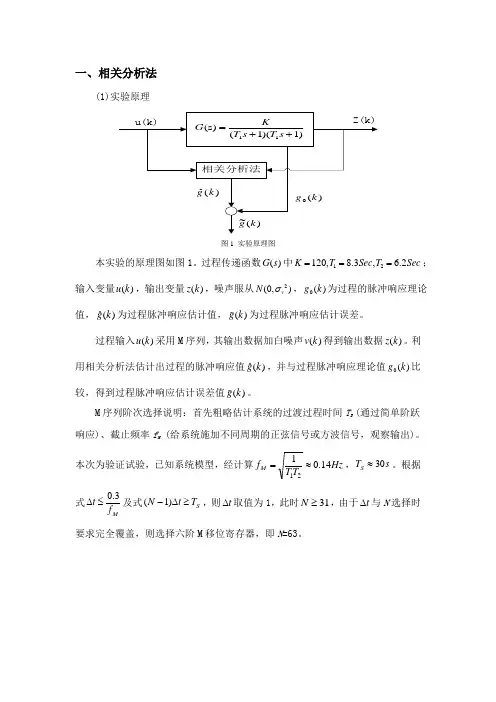
一、相关分析法(1)实验原理图1 实验原理图本实验的原理图如图1。
过程传递函数()G s 中12120,8.3, 6.2K T Sec T Sec ===；输入变量()u k ，输出变量()z k ，噪声服从2(0,)v N σ，0()g k 为过程的脉冲响应理论值，ˆ()gk 为过程脉冲响应估计值，()g k 为过程脉冲响应估计误差。
过程输入()u k 采用M 序列，其输出数据加白噪声()v k 得到输出数据()z k 。
利用相关分析法估计出过程的脉冲响应值ˆ()gk ，并与过程脉冲响应理论值0()g k 比较，得到过程脉冲响应估计误差值()g k 。
M 序列阶次选择说明：首先粗略估计系统的过渡过程时间T S (通过简单阶跃响应)、截止频率f M (给系统施加不同周期的正弦信号或方波信号，观察输出)。
本次为验证试验，已知系统模型，经计算Hz T T f M 14.0121≈=，s T S 30≈。
根据式Mf t 3.0≤∆及式S T t N ≥∆-)1(，则t ∆取值为1，此时31≥N ，由于t ∆与N 选择时要求完全覆盖，则选择六阶M 移位寄存器，即N =63。
(2)编程说明图2 程序流程图(3)分步说明 ① 生成M 序列：M 序列的循环周期63126=-=N ，时钟节拍1t Sec ∆=，幅度1a =，移位寄存器中第5、6位的内容按“模二相加”，反馈到第一位作为输入。
其中初始数据设为{1,0,1,0,0,0}。
程序如下：② 生成白噪声序列： 程序如下：③ 过程仿真得到输出数据：如图2所示的过程传递函数串联，可以写成形如121211()1/1/K Gs TT s T s T =++，其中112KK TT =。
图2 过程仿真方框图程序如下：④ 计算脉冲响应估计值：互相关函数采用公式)()(1)(10k i y i x Nr k R N r i xy +⋅⋅=∑-⋅=，互相关函数所用的数据是从第二个周期开始的，其中r 为周期数，取1-3之间。
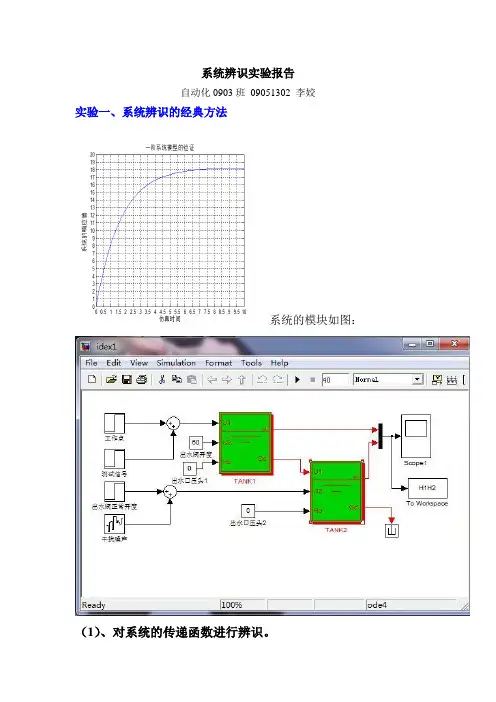
系统辨识实验报告自动化0903班09051302 李姣实验一、系统辨识的经典方法系统的模块如图：（1）、对系统的传递函数进行辨识。
对于一阶系统而言，未加入干扰信号时，其稳定值 t0=20.0，h0=42.2040， 加入干扰信号后其稳定值为 t=40，h1=60.4937。
现在分别取两个点为y1=30%对应的实际点为 h1’=42.2040+（60.4937-42.2040）*30%=47.6909； 根据实际测试值，选取h1’=47.8909，t1’=20.6，对应的 y1’=（47.89*09-42.2040）/（60.4939-42.2040）=0.3109 所以第一个点的取值为 y1’=0.3109；t1’=0.6； 同理可得第二个点的数值为 y2’=0.8033；t2’=2.7； 由公式 ：可得 T=1.6750；=0； 由公式可得 k=1.82899（2）、对传递函数进行检验下面对系统的辨识结果进行验证，用一个幅值为10的阶跃信号进行验证，程序如下： num=[1.82899]; den=[1.675,1];()()()()()()2112211212t t T ln 1Y ln 1Y t ln 1Y t ln 1Y ln 1Y ln 1Y -⎧=⎪---⎪⎨---⎪τ=⎪---⎩()y y K u u∞∆==∆∆t=[0:0.1:10];[y,x,t]=step(num,den,t);plot(t,10*y)grid on;title('一阶系统模型的验证');xlabel('仿真时间');ylabel('系统的响应值');set(gca,'xtick',[0:0.5:10]);set(gca,'ytick',[0:1:20]);所得的仿真图形如下，实际系统加入测试信号后0.5s，从workspace中可发现系统的响应值为h=47.0929-42.2040=4.8889；验证是的对应仿真值为h’=4.4720；其误差大小为：（4.8889-4.4720）/4.8889*100%=8.536%；同理，当仿真时间为3.8s时，h=16.3993；h’=16.398；误差大小为：（16.3993-16.398）/16.3993*100%=0.08%；所以经过验证个，可以确定该辨识结果可以反应该系统的传递函数。
北京工商大学《系统建模与辨识》课程上机实验报告（）专业名称：上机题目：离散模型的参数估计及阶次辨识专业班级：学生姓名：学号：指导教师：年月目录目录 (2)第一章实验目的 (3)第二章实验内容 (4)第三章基本最小二乘法 (6)3.1基本最小二乘法原理 (6)3.2基本最小二乘法实验结果 (7)3.3源程序代码 (12)第四章递推广义最小二乘法 (15)4.1递推广义最小二乘法原理 (15)4.2递推广义最小二乘法实验结果 (16)4.3源程序代码 (19)第五章遗忘因子递推最小二乘算法 (21)5.1遗忘因子递推最小二乘算法原理 (21)5.2遗忘因子递推最小二乘算法实验结果 (21)5.3源程序代码 (25)第六章递推随机逼近算法 (29)6.1递推随机逼近算法原理 (29)6.2递推随机逼近算法实验结果 (30)6.3源程序代码 (34)第七章AIC模型定阶 (37)7.1 AIC模型定阶原理 (37)7.2 AIC模型定阶实验结果 (37)7.3源程序代码 (37)第八章实验总结 (41)参考文献 (41)通过实验掌握几种常用的模型参数估计算法和阶次辨识理论，具体的模型参数估计方法包括基本最小二乘法、递推广义最小二乘法（RELS）、衰减因子的递推最小二乘法和递推随机逼近算法，并在实验的基础上总结体会不同辨识方法的适用范围和优缺点。
《过程辨识》书P538实验2 离散模型的参数估计及阶次辨识，选择模拟的是第一个过程，采用基本最小二乘法、递推广义最小二乘法（RELS ）、遗忘因子递推最小二乘法和递推随机逼近算法对被辨识系统进行参数估计，采用AIC 进行模型定阶。
1. 系统模拟图如图1所示图 1 系统模拟图 其中()()()()⎪⎪⎩⎪⎪⎨⎧=+-=+=+-=----------1.705.115.0.705.111211211211z D z z z C zz z B z z z A (1-1)输入信号()u k 采用幅值为1的M 序列，其特征多项式由实验者根据具体需要确定；()v k 是均值为零，方差为2v σ服从正态分布的不相关噪声，方差2v σ的大小由信噪比η确定。
《系统建模与及辨识》课程上机实验报告专业名称 ： 控制工程 上机题目 ： 用极大似然法进行参数估计一 实验目的通过实验掌握极大似然法在系统参数辨识中的原理和应用。
二 实验原理1 极大似然原理设有离散随机过程}{k V 与未知参数θ有关，假定已知概率分布密度)(θk V f 。
如果我们得到n 个独立的观测值,21,V V …n V ,，则可得分布密度)(1θV f ，)(2θV f ，…,)(θn V f 。
要求根据这些观测值来估计未知参数θ，估计的准则是观测值{}{k V }的出现概率为最大。
为此，定义一个似然函数)()()(),,,(2121θθθθn n V f V f V f V V V L = （1.1）上式的右边是n 个概率密度函数的连乘，似然函数L 是θ的函数。
如果L 达到极大值，}{k V 的出现概率为最大。
因此，极大似然法的实质就是求出使L 达到极大值的θ的估值∧θ。
为了便于求∧θ，对式（1.1）等号两边取对数，则把连乘变成连加，即 ∑==ni iV f L 1)(ln ln θ （1.2）由于对数函数是单调递增函数，当L 取极大值时，lnL 也同时取极大值。
求式（1.2）对θ的偏导数，令偏导数为0，可得ln =∂∂θL（1.3）解上式可得θ的极大似然估计ML ∧θ。
2 系统参数的极大似然估计Newton-Raphson 法实际上就是一种递推算法，可以用于在线辨识。
不过它是一种依每L 次观测数据递推一次的算法，现在我们讨论的是每观测一次数据就递推计算一次参数估计值得算法。
本质上说，它只是一种近似的极大似然法。
设系统的差分方程为 )()()()()(11k k u z b k y z a ξ+=-- （2.1） 式中111()1...nn a z a z a z ---=+++1101()...nn b z b b z b z---=+++因为)(k ξ是相关随机向量，故（2.1）可写成)()()()()()(111k z c k u z b k y z a ε---+= （2.2） 式中)()()(1k k z c ξε=- （2.3）nn z c z c z c ---+++= 1111)( （2.4）)(k ε是均值为0的高斯分布白噪声序列。
多项式)(1-z a ，)(1-z b 和)(1-z c 中的系数n n c c b b a a ,,,,,10,1和序列)}({k ε的均方差σ都是未知参数。
设待估参数n a a 1[=θ n b b 0 ]Tn c c 1 （2.5） 并设)(k y 的预测值为+-+++-----=∧∧∧∧∧)()()()1()(01n k u b k u b n k y a k y a k y n n)()1(1n k e c k e c n -++-∧∧（2.6） 式中)(i k e -为预测误差；i a ∧，i b ∧，i c ∧为i a ，i b ，i c 的估值。
预测误差可表示为+-+-⎢⎣⎡--=-=∑∑=∧=∧∧)()()()()()(01i k u b i k y a k y k y k y k e n i i n i i-+++-+++=⎥⎦⎤--∧-∧∧-∧-∧=∧∑)()()()1()(110111k u z b z b b k y z a z a i k e c nn n n ni i )()(2211k e z c z c z c n n -∧-∧-∧+++ （2.7）或者)()1(11k e z c z c nn -∧-∧+++ =-+++-∧-∧)()1(11k y z a z a nn)()(110k u z b z b b nn -∧-∧∧+++ （2.8） 因此预测误差{})(k e 满足关系式)()()()()()(111k u z b k y z a k e z c -∧-∧-∧-= （2.9） 式中n n z a z a z a -∧-∧-∧+++= 1111)( n n z b z b b z b -∧-∧∧-∧+++= 1101)( n n z c z c z c -∧-∧-∧+++= 1111)(假定预测误差)(k e 服从均值为0的高斯分布，并设序列{})(k e 具有相同的方差2σ。
因为{})(k e 与)(1-∧z c ，)(1-∧z a 和)(1-∧z b 有关，所以2σ是被估参数θ的函数。
为了书写方便，把式（2.9）写成)()()()()()(111k u z b k y z a k e z c ----= （2.10）-------++-+= )1()1()()1()()(101k u b k u b n k y a k y a k y k e n,2,1),()1()(1++=------n n k n k c k e c n k u b n n （2.11） 或写成)()()()()(11i k e c i k u b i k y a k y k e ni in i in i i-----+=∑∑∑=== （2.12）令k=n+1,n+2,…,n+N,可得)(k e 的N 个方程式，把这N 个方程式写成向量-矩阵形式θN N N Y e Φ-= （2.13） 式中⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++=)()2()1(N n y n y n y Y N ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++=)()2()1(N n e n e n e e N ,⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=n n b b a a 01θ⎢⎢⎢⎢⎣⎡-+-+--=Φ)1()1()(N n y n y n y N )()2()1(N y y y --- )()2()1(N n u n u n u +++ )()2()1(N u u u)1()1()(-++N n e n e n e ⎥⎥⎥⎥⎦⎤)()2()1(N e e e因为已假定{})(k e 是均值为0的高斯噪声序列，高斯噪声序列的概率密度函数为])(21ex p[)2(122212m y f --=σπσ （2.14）式中y 为观测值，2σ和m 为y 的方差和均值，那么)](21ex p[)2(122212k e f σπσ-=（2.15） 对于)(k e 符合高斯噪声序列的极大似然函数为)21exp()2(1)]}()2()1([21exp{)2(1])([])2([])1([])(,),2(),1([),(222222222NT N NN N e e N n e n e n e N n e f n e f n e f N n e n e n e L Y L σπσσπσθθθθσθ-=++++++-=+++=+++=（2.16）或]2)()(exp[)2(1),(222σθθπσσθΦ-Φ--=N T N NN Y Y Y L （2.17）对上式（2.17）等号两边取对数得N T N NT N NN e e N N e e Y L 2222221ln 22ln 2)21ex p(ln )2(1ln),(ln σσπσπσσθ---=-+= （2.18）或写为∑++=---=N n n k N k e N N Y L 1222)(21ln 22ln 2),(ln σσπσθ （2.19） 求),(ln σθN Y L 对2σ的偏导数，令其等于0，可得0)(212),(ln 12422=+-=∂∂∑++=N n n k N k e N Y L σσσσθ （2.20）则J N k e N k e NN n n k Nn n k 2)(212)(112122===∑∑++=++=∧σ （2.21） 式中∑++==N n n k k e J 12)(21 （2.22）2σ越小越好，因为当方差2σ最小时，)(2k e 最小，即残差最小。
因此希望2σ的估值取最小J Nmin 22=∧σ （2.23） 因为式（2.10）可理解为预测模型，而e(k)可看做预测误差。
因此使式（2.22）最小就是使误差的平方之和最小，即使对概率密度不作任何假设，这样的准则也是有意义的。
因此可按J 最小来求n n c c b b a a ,,,,,10,1的估计值。
由于e(k)式参数n n c c b b a a ,,,,,10,1的线性函数，因此J 是这些参数的二次型函数。
求使),(ln σθN Y L 最大的∧θ，等价于在式（2.10）的约束条件下求∧θ使J 为最小。
由于J 对i c 是非线性的，因而求J 的极小值问题并不好解，只能用迭代方法求解。
求J 极小值的常用迭代算法有拉格朗日乘子法和牛顿-拉卜森法。
下面介绍牛顿-拉卜森法。
整个迭代计算步骤如下：(1)确定初始的0∧θ值。
对于0∧θ中的n b b a a ,,,0,1可按模型)()()()()(11k u z b k y z a k e -∧-∧-= （2.24） 用最小二乘法来求，而对于0∧θ中的nc c ,1可先假定一些值。
(2)计算预测误差)()()(k y k y k e ∧-= （2.25） 给出∑++==N n n k k e J 12)(21并计算∑++=∧=Nn n k k eN 122)(1σ （2.26）(3)计算J 的梯度θ∂∂J和海赛矩阵 22θ∂∂J ,有 θθ∂∂=∂∂∑++=)()(1k e k e J N n n k （2.27） 式中⎢⎣⎡∂∂∂∂=∂∂n a k e a k e k e )()()(1 θ n b k e b k e ∂∂∂∂)()(0 Tn c k e c k e ⎥⎦⎤∂∂∂∂)()(1--------++-+∂∂=∂∂)()1()()()1()([)(101n k u b k u b k u b n k y a k y a k y a a k e n n i i )]()1(1n k e c k e c n ----in i i a n k e c a k e c a k e c i k y ∂-∂--∂-∂-∂-∂--=)()2()1()(21 （2.28） 即i nj j i a j k e c i k y a k e ∂-∂--=∂∂∑=)()()(1（2.29） 同理可得i n j j i b j k e c i k u b k e ∂-∂---=∂∂∑=)()()(1 （2.30） i n j j i c j k e c i k e c k e ∂-∂---=∂∂∑=)()()(1（2.31） 将式（2.29）移项化简，有in j j i n j j i a j k e c a j k e c a k e i k y ∂-∂=∂-∂+∂∂=-∑∑==)()()()(01 （2.32）因为j z k e j k e -=-)()( （2.33）由)(j k e -求偏导，故iji a z k e a j k e ∂∂=∂-∂-)()( （2.34） 将（2.34）代入（2.32），所以j nj j i i j n j j i nj j z c a k e a z k e c a j k e c i k y -=-==∑∑∑∂∂=∂∂=∂-∂=-000)()()()( （2.35） n n z c z c z c ---+++= 1111)(所以得)()()(1i k y a k e z c i-=∂∂- （2.36） 同理可得（2.30）和（2.31）为 )()()(1i k u b k e z c i--=∂∂- （2.37） )()()(1i k e c k e z c i--=∂∂- （2.38） 根据（2.36）构造公式)(])([)]([)(1i k y j j i k y a j i k e z c j-=---=∂--∂- （2.39）将其代入（2.36），可得ij a k e z c a j i k e z c ∂∂=∂--∂--)()()]([)(11 (2.40）消除)(1-z c 可得1)1()()(a i k e a j i k e a k e j i ∂+-∂=∂+-∂=∂∂ （2.41） 同理可得（2.37）和（2.38）式)()()(b i k e b j i k e b k e j i ∂-∂=∂+-∂=∂∂ （2.42）1)1()()(c i k e c j i k e c k e j i ∂+-∂=∂+-∂=∂∂ （2.43） 式（2.29）、式（2.30）和式（2.31）均为差分方程，这些差分方程的初始条件为0，可通过求解这些差分方程，分别求出e(k)关于n n c c b b a a ,,,,,10,1的全部偏导数，而这些偏导数分别为)}({k y ，)}({k u 和)}({k e 的线性函数。
