下载文档原格式
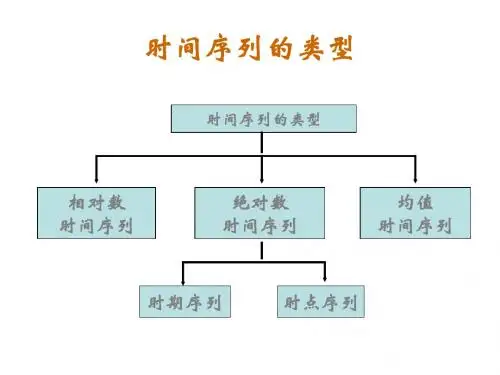
时间序列分析时间序列数据的特点是观测值之间存在时间上的依赖关系，即一个观测值的取值可能与之前的多个观测值存在相关性。
时间序列分析主要考虑以下几个方面：1. 趋势分析：时间序列数据中存在的长期增长或下降趋势可以通过趋势分析来判断。
趋势分析可以采用移动平均法、指数平滑法等方法来拟合趋势线，从而预测未来的趋势。
2. 季节性分析：时间序列数据中的季节性波动是一种按照固定的季节循环出现的规律变动。
季节性分析可以通过季节性指数、分解法等方法来对季节性波动进行分析和预测。
3. 周期性分析：周期性是指时间序列数据中存在的较长周期的波动。
周期性分析可以通过傅里叶分析、自相关函数等方法来分析和预测周期性波动。
4. 随机性分析：时间序列数据中的随机变动是指除趋势、季节性、周期性之外的不可预测的波动。
随机性分析可以通过残差项的分析来判断数据中是否存在随机波动。
时间序列分析的方法包括统计方法和经典时间序列分析方法。
统计方法主要包括自回归移动平均模型（ARMA）、自回归积分移动平均模型（ARIMA）等。
经典时间序列分析方法主要包括指数平滑法、趋势法、季节性指数法等。
时间序列分析的应用领域广泛。
在经济学中，时间序列分析可以用来预测经济指标的变动趋势，为政府决策提供依据。
在金融学中，时间序列分析可以用来预测股市的走势，帮助投资者制定投资策略。
在气象学中，时间序列分析可以用来预测天气变化，为农民和旅行者提供参考。
在医学中，时间序列分析可以用来预测疾病的传播趋势，为疾病防控提供支持。
然而，时间序列分析也存在一些挑战和限制。
首先，时间序列数据的质量和可靠性对分析结果的影响很大，因此数据的采集、清洗和处理是很重要的。
其次，时间序列数据的非线性和非平稳性使得分析方法的选择和应用更为复杂。
此外，时间序列数据同时受到多种因素的影响，如外部环境、政策变化等，这些因素需要合理地加以考虑。
总的来说，时间序列分析是一种重要的统计分析方法，可以用来揭示时间序列数据内部的潜在规律和特征，并通过对过去数据的观察和分析来预测未来的趋势。
时间序列分析时间序列分析是一种用来研究时间相关数据的统计方法。
它可以帮助我们了解时间序列的趋势、周期性和季节性，以及预测未来的发展趋势。
在此，我将介绍时间序列分析的基本原理、常用模型和实际应用。
时间序列分析的基本原理可以总结为以下几个步骤：收集时间序列数据、检验序列的平稳性、拟合适当的模型、进行模型诊断、进行预测和模型评估。
首先，收集时间序列数据是进行时间序列分析的前提。
时间序列数据是按照时间顺序排列的一组观测值，例如经济指标、股票价格或气温记录等。
接下来，我们需要检验时间序列的平稳性。
平稳性是指时间序列在统计特征上不随时间变化而变化的性质。
平稳时间序列的均值和方差是恒定的，并且自相关系数不随时间而变化。
然后，我们可以选择适当的时间序列模型来拟合数据。
常用的时间序列模型包括自回归移动平均模型（ARMA）、自回归积分移动平均模型（ARIMA）和季节性自回归积分移动平均模型（SARIMA）等。
在拟合模型之后，我们需要进行模型诊断来检验模型的拟合优度。
模型诊断的目标是检查模型的残差是否符合模型假设。
常用的诊断方法包括检查残差的自相关性、偏自相关性和正态性等。
最后，我们可以利用拟合好的模型进行预测。
预测是时间序列分析中最常用的应用之一，可以帮助我们预测未来的发展趋势。
常用的预测方法包括滚动预测和动态预测等。
时间序列分析具有广泛的应用领域。
在经济学中，时间序列分析被广泛应用于金融市场的预测、货币政策的研究以及宏观经济的分析等。
在气象学中，时间序列分析可以帮助我们预测天气的变化和气候的长期趋势。
在医学领域，时间序列分析可以用来研究疾病的发展趋势和预测疾病的传播范围。
总之，时间序列分析是一种强大的工具，可以帮助我们理解时间序列数据的特征，预测未来的发展趋势，并从中获得有用的信息。
在实际应用中，研究人员需要根据具体问题选择合适的模型和方法，并进行模型诊断和评估。
通过深入研究时间序列分析，我们将能够更好地理解时间序列的本质，为实际问题提供更准确的预测和决策支持。
